Thermodynamics and Thermochemistry 1 Question 39
42. An ideal gas in thermally insulated vessel at internal pressure $=p_{1}$, volume $=V_{1}$ and absolute temperature $=T_{1}$ expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are $p_{2}, V_{2}$ and $T_{2}$, respectively. For this expansion
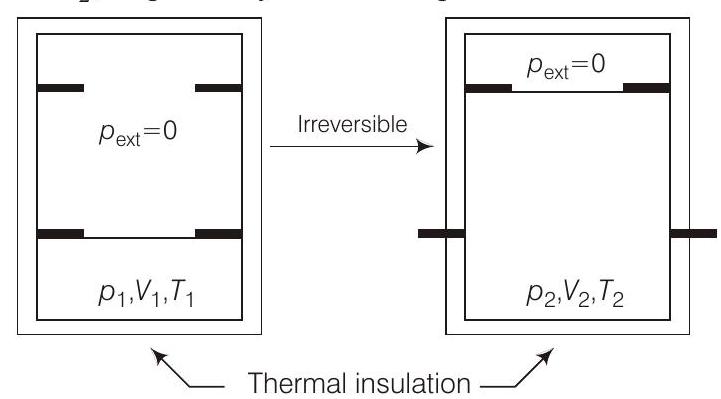
(a) $q=0$
(b) $T_{2}=T_{1}$
(c) $p_{2} V_{2}=p_{1} V_{1}$
(d) $p_{2} V_{2}^{\gamma}=p_{1} V_{1}^{\gamma}$
(2014 Adv.)
Show Answer
Solution:
- PLAN This problem includes concept of isothermal adiabatic irreversible expansion.
Process is adiabatic because of the use of thermal insolution therefore, $q=0$
$$ \because \quad p_{\text {ext }}=0 $$
$$ w=p_{\mathrm{ext}} \cdot \Delta V=0 \times \Delta V=0 $$
Internal energy can be written as
$$ \Delta U=q+W=0 $$
The change in internal energy of an ideal gas depends only on temperature and change in internal energy $(\Delta U)=0$ therefore, $\Delta T=0$ hence, process is isothermal and
and
$$ \begin{gathered} T_{2}=T_{1} \ p_{2} V_{2}=p_{1} V_{1} \end{gathered} $$
(d) $p_{2} V_{2}^{\gamma}=p_{1} V_{1}^{\gamma}$ is incorrect, it is valid for adiabatic reversible process.
Hence, only (a), (b) and (c) are correct choices.










