Solutions and Colligative Properties 2 Question 7
7. Freezing point of a $4 %$ aqueous solution of $X$ is equal to freezing point of $12 %$ aqueous solution of $Y$. If molecular weight of $X$ is $A$, then molecular weight of $Y$ is
(2019 Main, 12 Jan I)
(a) $4 \mathrm{~A}$
(b) $2 \mathrm{~A}$
(c) $3 \mathrm{~A}$
(d) A
Show Answer
Solution:
- Given, Freezing point of $4 %$ aqueous solution of $X$.
$=$ Freezing point of $12 %$ aqueous solution of $Y$
$$ \text { or } \begin{aligned} \left(\Delta T_{f}\right){X} & =\left(\Delta T{f}\right){Y} \quad\left[\because \Delta T{f}=T_{f}^{\circ}-T_{f}\right] \ K_{f} \times m_{X} & =K_{f} m_{Y} \end{aligned} $$
where, $m_{X}$ and $m_{Y}$ are molality of $X$ and $Y$, respectively.
or
$$ m_{X}=m_{Y} $$
Now, $\quad$ molality $=\frac{\text { Number of moles of solute }(n)}{\text { Mass of solvent (in kg) }}$
$n=\frac{\text { Weight }}{\text { Molecular mass }}$
$\frac{w_{X}}{M_{X} \times\left(w_{\text {solvent }}\right){1}}=\frac{w{Y}}{M_{Y} \times\left(w_{\text {solvent }}\right)_{2}}$
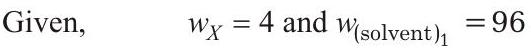
$w_{Y}=12$ and $w_{\text {(solvent) }_{2}}=88$
$M_{X}=A$
$\therefore \quad \frac{4 \times 1000}{M_{X} \times 96}=\frac{12 \times 1000}{M_{Y} \times 88}$
Thus, $\quad M_{Y}=\frac{12 \times 1000 \times M_{X} \times 96}{4 \times 1000 \times 88}$
$=\frac{96 \times 12}{4 \times 88} \times \mathrm{A}=3.27 \mathrm{~A} \approx 3 \mathrm{~A}$










