Solutions and Colligative Properties 2 Question 6
6. Molecules of benzoic acid $\left(\mathrm{C}{6} \mathrm{H}{5} \mathrm{COOH}\right)$ dimerise in benzene. ’ $w$ ’ $\mathrm{g}$ of the acid dissolved in $30 \mathrm{~g}$ of benzene shows a depression in freezing point equal to $2 \mathrm{~K}$. If the percentage association of the acid to form dimer in the solution is 80 , then $w$ is
(Given that $K_{f}=5 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}$, molar mass of benzoic $\operatorname{acid}=122 \mathrm{~g} \mathrm{~mol}^{-1}$ )
(2019 Main, 12 Jan II)
(a) $1.8 \mathrm{~g}$
(b) $1.0 \mathrm{~g}$
(c) $2.4 \mathrm{~g}$
(d) $1.5 \mathrm{~g}$
Show Answer
Solution:
- Molecules of benzoic acid dimerise in benzene as:
$$ 2\left(\mathrm{C}{6} \mathrm{H}{5} \mathrm{COOH}\right) \rightleftharpoons\left(\mathrm{C}{6} \mathrm{H}{5} \mathrm{COOH}\right)_{2} $$
Now, we know that depression in freezing point $\left(\Delta T_{f}\right)$ is given by following equation:
$\Delta T_{f}=i \times K_{f} \times m=\frac{i \times K_{f} \times w_{\text {solute }} \times 1000}{M w_{\text {solute }} \times w_{\text {solvent }}}$
Given, $w_{\text {solute }}($ benzoic acid $)=w \mathrm{~g}$
$$ w_{\text {solvent }}(\text { benzene })=30 \mathrm{~g} $$
$M w_{\text {Solute }}($ benzoic acid $)=122 \mathrm{~g} \mathrm{~mol}^{-1}, \Delta T_{f}=2 \mathrm{~K}$
$K_{f}=5 \mathrm{Kkg} \mathrm{mol}^{-1}, % \alpha=80$ or $\alpha=0.8$
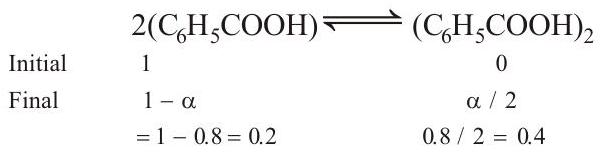
Total number of moles at equilibrium $=0.2+0.4=0.6$
$$ i=\frac{\text { Number of moles at equilibrium }}{\text { Number of moles present initially }} $$
$$ i=\frac{0.6}{1}=0.6 $$
On substituting all the given values in Eq. (i), we get
$$ 2=\frac{0.6 \times 5 \times w \times 1000}{122 \times 30}, \quad w=2.44 \mathrm{~g} $$
Thus, weight of acid $(w)$ is $2.4 \mathrm{~g}$.










