Solutions and Colligative Properties 1 Question 3
4. For the solution of the gases $w, x, y$ and $z$ in water at $298 \mathrm{~K}$, the Henry’s law constants $\left(K_{\mathrm{H}}\right)$ are $0.5,2,35$ and $40 \mathrm{~K}$ bar, respectively. The correct plot for the given data is
(2019 Main, 8 April II) (a)
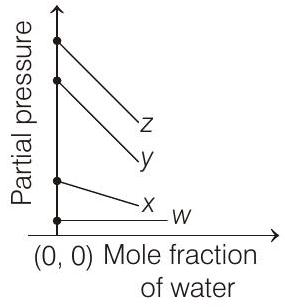
(c)
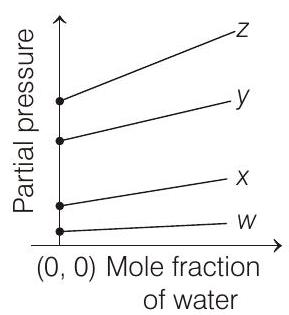
(b)
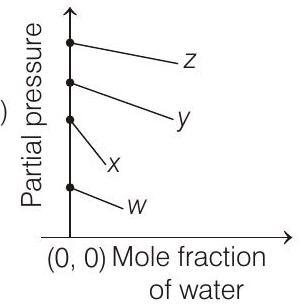
(d)
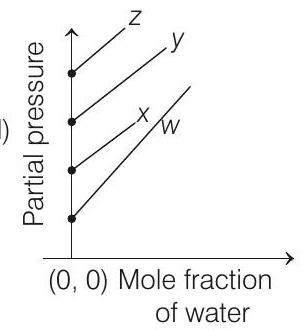
Show Answer
Solution:
- According to Henry’s law (at constant temperature)
$p_{\text {gas }}=K_{\mathrm{H}} \times \chi_{\text {gas (solute) }}=K_{\mathrm{H}} \times\left[1-\chi_{\mathrm{H}_{2} \mathrm{O} \text { (solvent) }}\right]$
$p_{\text {gas }}=K_{\mathrm{H}}-K_{\mathrm{H}} \chi_{\mathrm{H}{2} \mathrm{O}}$ $p{\text {gas }}=$ partial pressure of the gas above its solution with a liquid (solvent) say water.
$\chi_{\text {gas }}=$ mole fraction of the gas (solute) in the solution.
$\chi_{\mathrm{H}_{2} \mathrm{O}}=$ mole fraction of water (solvent).
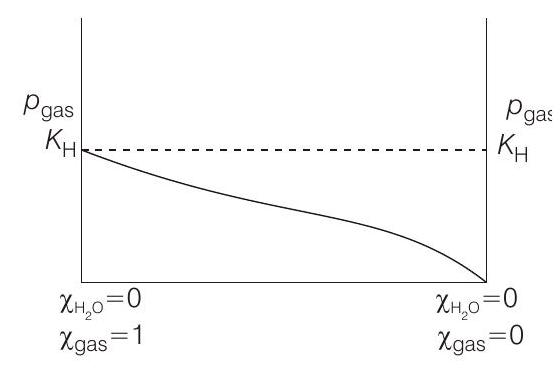
[i.e. $p_{\text {gas }}=K_{\mathrm{H}}$ ] Higher the value of $K_{\mathrm{H}}$, higher
will be the partial pressure of the gas $\left(p_{\text {gas }}\right)$, at a given temperature. The plot of $p_{\text {gas }} v s \chi_{\mathrm{H}_{2} \mathrm{O}}$ gives a (-ve) slope.
$$ p_{\text {gas }}=K_{\mathrm{H}}-K_{\mathrm{H}} \times \chi_{\mathrm{H}_{2} \mathrm{O}} $$
Comparing the above equation with the equation of straight line $y=m x+c$
Slope $=-K_{\mathrm{H}}$, intercept $=K_{\mathrm{H}}$
So, (i) Higher the value of $K_{\mathrm{H}}$, more (-ve) will be the slope and it is for $z\left(K_{\mathrm{H}}=40 \mathrm{~K}\right.$ bar $)$
(ii) Higher the value of $K_{\mathrm{H}}$, higher with the value of intercept, i.e. partial pressure and it is also for $z$.










