Electrochemistry 2 Question 16
15. The standard reduction potential data at $25^{\circ} \mathrm{C}$ is given below. $E^{\circ}\left(\mathrm{Fe}^{3+} / \mathrm{Fe}^{2+}\right)=+0.77 \mathrm{~V} ; E^{\circ}\left(\mathrm{Fe}^{2} / \mathrm{Fe}\right)=-0.44 \mathrm{~V}$;
$E^{\circ}\left(\mathrm{Cu}^{2+} / \mathrm{Cu}\right)=+0.34 \mathrm{~V} ; E^{\circ}\left(\mathrm{Cu}^{+} / \mathrm{Cu}\right)=+0.52 \mathrm{~V} ;$
$\left.E^{\circ}\left(\mathrm{O}{2}(g)+4 \mathrm{H}^{+}+4 e^{-}\right) \longrightarrow 2 \mathrm{H}{2} \mathrm{O}\right)=+1.23 \mathrm{~V}$;
$\left.E^{\circ}\left(\mathrm{O}{2}(g)+2 \mathrm{H}{2} \mathrm{O}+4 e^{-}\right) \longrightarrow 4 \mathrm{OH}\right)=+0.40 \mathrm{~V}$
$E^{\circ}\left(\mathrm{Cr}^{3+} / \mathrm{Cr}\right)=-0.74 \mathrm{~V} ; E^{\circ}\left(\mathrm{Cr}^{2+} / \mathrm{Cr}\right)=+0.91 \mathrm{~V}$
Match $E^{\circ}$ of the rebox pair in Column I with the values given in Column II and select the correct answer using the code given below the lists.
(2013 Adv.)
| Column I | Column II | ||
|---|---|---|---|
| P. | $E^{\circ}\left(\mathrm{Fe}^{3+} / \mathrm{Fe}\right)$ | 1. | $-0.18 \mathrm{~V}$ |
| Q. | $E^{\circ}\left(4 \mathrm{H}_{2} \mathrm{O} \rightleftharpoons 4 \mathrm{H}^{+}+4 \mathrm{OH}^{-}\right)$ | 2. | $-0.4 \mathrm{~V}$ |
| R. | $E^{\circ}\left(\mathrm{Cu}^{2+}+\mathrm{Cu} \longrightarrow 2 \mathrm{Cu}^{+}\right)$ | 3. | $-0.04 \mathrm{~V}$ |
| S. | $E^{\circ}\left(\mathrm{Cr}^{3+}, \mathrm{Cr}^{2+}\right)$ | 4. | $-0.83 \mathrm{~V}$ |
Codes
| P | Q | R | S | |
|---|---|---|---|---|
| (a) | 4 | 1 | 2 | 3 |
| (b) | 2 | 3 | 4 | 1 |
| (c) | 1 | 2 | 3 | 4 |
| (d) | 3 | 4 | 1 | 2 |
Show Answer
Solution:
- PLAN When different number of electrons are involved in a redox reaction
$$ \begin{aligned} \Delta G_{\text {net }}^{\circ} & =\Delta G_{1}^{\circ}+\Delta G_{2}^{\circ} \ -n_{3} F E^{\circ}{ }{3} & =-n{1} F E_{1}^{\circ}-n_{2} F E^{\circ}{ }{2} \ \therefore \quad E^{\circ}{ }{3} & =\frac{n_{1} E_{1}^{\circ}+n_{2} E_{2}^{\circ}}{n_{3}} \end{aligned} $$
(P) $E_{3}^{\circ} \mathrm{Fe}^{3+} / \mathrm{Fe}$
Net reaction $\mathrm{Fe}^{3+} \longrightarrow \mathrm{Fe}$
is obtained from
$\mathrm{Fe}^{3+}+e^{-} \longrightarrow \mathrm{Fe}^{2+} \quad n_{1}=1 \quad E_{1}^{\text {od }}=0.77 \mathrm{~V}$
$\mathrm{Fe}^{2+}+2 e^{-} \longrightarrow \mathrm{Fe} \quad n_{2}=2 \quad E_{2}^{\circ}=-0.44 \mathrm{~V}$
$\because \overline{\mathrm{Fe}^{3+}+3 e^{-} \longrightarrow \mathrm{Fe}} \quad n_{3}=3 \quad E_{3}^{\circ}=$ ?
$E^{\circ}{ }{3}=\frac{n{1} E^{\circ}{ }{1}+n{2} E^{\circ}{ }{2}}{n{3}}=\frac{0.77+2(-0.44)}{3}=\frac{-0.11}{3}=-0.04 \mathrm{~V}$
Thus, $\mathrm{P}$ - (3)
Net reaction
$$ 4 \mathrm{H}_{2} \mathrm{O} \rightleftharpoons 4 \mathrm{H}^{+}+4 \mathrm{OH}^{-} $$
is obtained from
$$ \begin{array}{cc} n & E^{\circ} \ n_{1}=4 & -1.23 \mathrm{~V} \ n_{2}=4 & +0.40 \mathrm{~V} \ n_{3}=4 & ? \end{array} $$
$2 \mathrm{H}{2} \mathrm{O} \longrightarrow \mathrm{O}{2}+4 \mathrm{H}^{+}+4 e^{-}$
$2 \mathrm{H}{2} \mathrm{O}+\mathrm{O}{2}+4 e^{-} \longrightarrow 4 \mathrm{OH}^{-}$
$4 \mathrm{H}_{2} \mathrm{O} \longrightarrow 4 \mathrm{H}^{+}+4 e^{-}$
$E^{\circ}{ }{3}=\frac{n{1} E_{1}^{\circ}+n_{2} E^{\circ}{ }{2}}{n{3}}=E^{\circ}{ }{1}+E^{\circ}{ }{2}$
$$ =-1.23+0.40=-0.83 \mathrm{~V} $$
Thus, Q - (4)
(R) $\mathrm{Cu}^{2+}+\mathrm{Cu} \longrightarrow 2 \mathrm{Cu}^{+}$
For thus $E^{\circ}$ of $\mathrm{Cu}^{2+} \longrightarrow \mathrm{Cu}^{+}$
is also required.
$$ \begin{aligned} & \mathrm{Cu}^{2+}+2 e^{-} \longrightarrow \mathrm{Cu} \ & \mathrm{Cu} \longrightarrow \mathrm{Cu}^{+}+e^{-} \quad 1 \quad-0.52 \mathrm{~V} \ & \overline{\mathrm{Cu}^{2+}+e^{-} \longrightarrow \mathrm{Cu}^{+}} \quad E^{\circ}{ }{3} \quad ? \ & E{3}{ }^{\circ}=\frac{n_{1} E_{1}{ }^{\circ}+n_{2} E_{2}{ }^{\circ}}{n_{3}}=\frac{2 \times 0.34+1 \times(-0.52)}{1}=0.16 \mathrm{~V} \end{aligned} $$
$$ \begin{aligned} & \underline{n} \quad E^{\circ} \ & \mathrm{Cu} \longrightarrow \mathrm{Cu}^{+}+e^{-} \quad n_{1}=1, \quad-0.52 \mathrm{~V} \ & \mathrm{Cu}^{2+}+e^{-} \longrightarrow \mathrm{Cu}^{+} \quad n_{2}=1 \quad 0.10 \mathrm{~V} \ & \mathrm{Cu}^{2+}+\mathrm{Cu} \longrightarrow 2 \mathrm{Cu}^{+} \ & E^{\circ}=-0.52+0.16=-0.36 \mathrm{~V} \end{aligned} $$
Thus, $(\mathrm{R})-(1)$ (S) $\mathrm{Cr}^{3+} \longrightarrow \mathrm{Cr}^{2+}$
is obtained from $\mathrm{Cr}^{3+}+3 e^{-} \longrightarrow \mathrm{Cr}$ $\mathrm{Cr} \longrightarrow \mathrm{Cr}^{2+}+2 e^{-}$
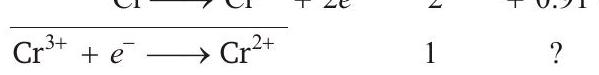
$E_{3}{ }^{\circ}=\frac{-0.74 \times 3+2 \times 0.91}{1}=-0.4 \mathrm{~V}$
Thus, $S=(2)$
$\mathrm{P}-(3), \mathrm{Q}-(4), \mathrm{R}-(1), \mathrm{S}-(2)$










