Electrochemistry 1 Question 27
27. For the electrochemical cell, $\operatorname{Mg}(s)\left|\mathrm{Mg}^{2+}(a q, 1 \mathrm{M}) | \mathrm{Cu}^{2+}(a q, 1 \mathrm{M})\right| \mathrm{Cu}(s)$
The standard emf of the cell is $2.70 \mathrm{~V}$ at $300 \mathrm{~K}$. When the concentration of $\mathrm{Mg}^{2+}$ is changed to $x \mathrm{M}$, the cell potential changes to $2.67 \mathrm{~V}$ at $300 \mathrm{~K}$. The value of $x$ is (Given, $\frac{F}{R}=11500 \mathrm{~K} \mathrm{~V}^{-1}$, where $F$ is the Faraday constant and $R$ is the gas contant, $\operatorname{In}(10)=2.30)$
(2018 Adv.)
Show Answer
Answer:
Correct Answer: 27. $(1.4085 \mathrm{M})$
)
Solution:
- (10) Equation of cell reaction according to the cell notation given, is
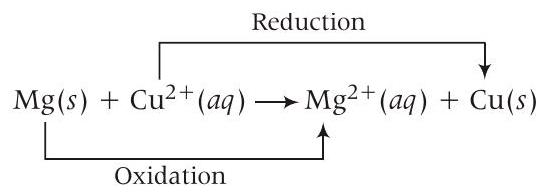
Given, $E_{\text {cell }}^{\circ}=2.70 \mathrm{~V}, T=300 \mathrm{~K}$
with $\quad\left[\mathrm{Mg}^{2+}(a q)\right]=1 \mathrm{M}$ and $\left[\mathrm{Cu}^{2+}(a q)\right]=1 \mathrm{M}$
and $n=2$
Further, $\quad E_{\text {cell }}=2.67 \mathrm{~V}$
with $\quad\left[\mathrm{Cu}^{2+}(a q)\right]=1 \mathrm{M}$
and $\quad\left[\mathrm{Mg}^{2+}(a q)\right]=x \mathrm{M}$
and $\quad \frac{F}{R}=11500 \mathrm{KV}^{-1}$
where $F=$ Faraday constant, $R=$ gas constant From the formula,
$$ E_{\text {cell }}=E_{\text {cell }}^{\circ}-\frac{R T}{n F} \ln \frac{\left[\mathrm{Mg}^{2+}(a q)\right]}{\left[\mathrm{Cu}^{2+}(a q)\right]} $$
After putting the given values
$$ \begin{aligned}










