अध्याय 8

गुरुत्वाकर्षण

MCQ I

8.1 पृथ्वी एक प्राकृतिक गोलकार है। यदि उसके अंतर्गत सभी स्थान पर भूतल पर अधिकतम घनत्व न हो, तो पृथ्वी की सतह पर गुरुत्व के कारण त्वरण

(a) मध्य में ही दिशा में होगी लेकिन सभी स्थानों पर समान नहीं होगी।

(b) हर स्थान पर समान मान रखेगी लेकिन मध्य में नहीं होगी।

(c) माग्नीतुदिशा में समान होगी।

(d) किसी भी बिंदु पर शून्य नहीं हो सकती।

8.2 पृथ्वी से देखने पर, सूर्य एक आकस्मिक वृत्तकार में चलता है। दूसरे ग्रह जैसे मर्कुरी की पृथ्वी से देखी गई गति के लिए यह

(a) उसी तरह सच होगा।

(b) सच नहीं होगा क्योंकि पृथ्वी और मर्कुरी के बीच के बाल एकवर्ती वर्ग कानून नहीं है।

(c) सच नहीं होगा क्योंकि मर्कुरी पर परम गुरुत्वाकर्षण बाल सलाह में नहीं है।

(d) सच नहीं होगा क्योंकि मर्कुरी को गुरुत्वाकर्षण बाल के अलावा अन्य बाल भी प्रभावित करते हैं।

8.3 पृथ्वी के विभिन्न बिंदु सूर्य से थोड़ी सी दूरी पर होते हैं और इसलिए गुरुत्वाकर्षण के कारण विभिन्न बाल को भोगते हैं। एक ठोस शरीर के लिए, हम जानते हैं कि यदि विभिन्न बिंदुओं में विभिन्न बाल बारेंद्रिय पर करेंगे, तो परिणामकारी चाल यही होगी कि धारणा पर कोई पूर्ण प्रभाव करेगी (माध्य के माध्यम से एक प्रकार का वैक्टरी चाल) और माध्य पर नेट टौर्क (माध्य के माध्यम से एक धुरी द्वारा घिरी चढ़ाई) के द्वारा घिरी चाल कि परिभाषा में घूमना। पृथ्वी-सूर्य प्रणाली के लिए (पृथ्वी को एक सामान्य घनत्व गोलकार के रूप में अनुमानित करके)

(a) टॉर्क शून्य है।

(b) टॉर्क पृथ्वी को घूमाता है।

(c) धारणा शरीर परिणाम लागू नहीं होता क्योंकि पृथ्वी न केवल कम से कम एक कठिन शरीर है।

(d) टॉर्क पृथ्वी को सूर्य के आसपास घूमने का कारण होता है।

8.4 पृथ्वी के चारों ओर चक्रवात में उपग्रहों की प्रायोज्य जीवन होता है और कभी-कभी उपग्रह के अवशेष पृथ्वी पर गिर जाते हैं। यह इसलिए है,

(a) उपग्रह में सौर ऊर्जा की कोशिकाएँ और बैटरी खत्म हो जाती हैं।

(b) गुरुत्वाकर्षण के कानूनों ने एक आकारिक वमिकता यात्रा की पूर्वानुमान की है।

(c) पासून बाल की गति और ऊंचाई को धीरे-धीरे कम करने के कारण दृव्यमान के कारण चिपचिपापन के बाल होते हैं।

(d) अन्य उपग्रहों के साथ संघर्ष के कारण।

8.5 पृथ्वी और चंद्रमा दोनों सूर्य के गुरुत्वाकर्षण बाल के प्रभाव में होते हैं। सूर्य से देखी गई क्रमवार चंद्रमा की ओरबंध

(a) अर्द्धवृत्ताकार होगा।

(b) बिल्कुल निश्चित रूप से अर्धवृत्ताकार नहीं होगा क्योंकि इस पर कुल गुरुत्वाकर्षण बाल केंद्रीय नहीं होता है।

(c) अर्धवृत्ताकार नहीं होता है, लेकिन आवश्यकतानुसार बंद मत्तली होगा।

(d) पृथ्वी के अलावा अन्य ग्रहों के प्रभाव के कारण व्यापक रूप से गोलाकार से भटकता है।

8.6 हमारे सौरमंडल में, अंतर ग्रहीय क्षेत्र में ग्रहों के समानुदेश में टुकड़े मिलते हैं (आकार में ग्रहों की तुलना में काफी छोटे) अजगर इन्हें

(a) सूर्य की तुलना में घूमते नहीं हैं क्योंकि वे सूर्य की तुलना में बहुत छोटे मात्रा के साथ होते हैं।

(b) अनियमित रूप से लगेंगे क्योंकि उनके मात्रा छोटे होते हैं और बाहरी खिलाड़ियों की तरफ हट जाते हैं।

(c) सूर्य के चारों ओर बंद ओर्बिट में घूमेंगे, लेकिन केप्लर के कानूनों का पालन नहीं करेंगे।

(d) ग्रहों के आकार में और केपलर के कानूनों का पालन करने वाले खिलाड़ियों की तरह बंदमतल चालेंगे।

8.7 गलत विकल्प चुनें।

(a) गतिशील भार एक बाह्य बल द्वारा शरीर को गतिशील करने की समस्या का माप होता है जबकि भौतिक भार एक बाह्य भार पर उस पर भौतिकीय बल को निर्धारित करने में उपयुक्त होता है।

(b) यह कि भौतिक भार और गतिशील भार समान होते हैं एक प्रयोगात्मक परिणाम है।

(c) यह कि पृथ्वी पर गुरुत्वाकर्षण से होने वाला त्वरण सभी शरीरों के लिए समान होता है, यहाँ तक कि गुरुत्वाकर्षण भार और गतिशील भार के समानता के कारण होता है।

(d) प्रोटॉन जैसे कण का गुरुत्वाकर्षण भार पड़ोसी भारी वस्तुओं की हाजिरी पर निर्भर कर सकता है लेकिन गतिशील भार यह नहीं कर सकता।

8.8 पार्टिकलों का भार $2 M, m$ और $M$ हैं जो संबंधी रूप से बिंदुओं A, B और C पर हैं जहाँ $\mathrm{AB}=1 / 2(\mathrm{BC})$ है। $m$ $M$ की तुलना में बहुत छोटा है और समय $t=0$ पर वे सभी शांत हैं (फ़िगर 8.1)।

किसी भी संघर्ष के पहले समय पर:

फ़िगर 8.1

(a) $m$ शांत रहेगा।

(b) $m$ $M$ की ओर चलेगा।

(c) $m$ $2 M$ की ओर चलेगा।

(d) $m$ धारणिक गति होगा।

MCQ II

8.9 निम्नलिखित में से कौन से विकल्प सही हैं?

(a) गुरुत्वाकर्षण द्वारा होने वाला त्वरण ऊँचाई बढ़ने पर कम होता है।

(b) गुरुत्वाकर्षण द्वारा होने वाला त्वरण गहराई बढ़ने पर बढ़ता है। (पृथ्वी को यूनिफार्म घनत्व के एक गोलाकार माने)

(c) गुरुत्वाकर्षण द्वारा होने वाला त्वरण अक्षांश के साथ बढ़ता है।

(d) गुरुत्वाकर्षण द्वारा होने वाला त्वरण पृथ्वी के भार पर निर्भर नहीं होता।

8.10 अगर गुरुत्वाकर्षण का नियम बिजपुंज का बजाय तिगुना बज का हो जाता है-

(a) ग्रह अपवादी परिक्रमा नहीं करेंगे।

(b) ग्रहों का वृत्ताकार परिक्रमा संभव नहीं है।

(c) पृथ्वी की सतह पर हाथ से बाइंदविक मोशन का संकेत होगा।

(d) एक समान घनत्व वाले गोलाकार कपड़े के गोलाकार छलना के भीतर कोई गुरुत्वाकर्षण बल नहीं होगा।

8.11 अगर सूर्य का भार दस गुना छोटा होता है और गुरुत्वाकर्षण संकेत $G$ दस गुना बड़ा होता है (मात्राएं में)-

(a) भूमि पर चलना ज़्यादा मुश्किल हो जाएगा।

(b) पृथ्वी पर गुरुत्वाकर्षण के त्वरण में कोई बदलाव नहीं होगा।

(c) वर्षा की बूँदें बहुत तेज़ गिरेंगी।

(d) हवाई जहाज़ ज़्यादा तेज़ चलने होंगे।

8.12 अगर सूर्य और ग्रहों पर भारी मात्रा में संदर्भी प्राष्ट साथ लेते हैं,

(a) केपलर के सभी तीन कानून अभी भी वैध होंगे।

(b) सिर्फ़ तीसरा कानून वैध होगा।

(c) दूसरा कानून नहीं बदलेगा।

(d) पहला कानून अभी भी वैध होगा।

8.13 एक सुझाव है कि बहुत विशाल समय अवधि (अरबों वर्षों में) में गुरुत्वाकर्षणीय संख्या $G$ की मान छोटी हो जाती है। अगर ऐसा होता है, तो हमारी पृथ्वी के लिए,

(a) कुछ भी बदल नहीं जाएगा।

(b) हम अरबों सालों बाद गर्म हो जाएंगे।

(c) हम इधर-उधर घूमते रहेंगे, लेकिन सख्तता के साथ बंदोबस्त की आवधि नहीं होगी।

(d) सुबह-शाम के पर्याप्त लम्बे समय बाद हम उर्जा सिस्टम छोड़ देंगे।

उच्चारण 8.14 न्यूटन के गुरुत्वाकर्षण के लिए नियम को मानते हुए जब गुरुत्वाकर्षण बल $\mathbf{F_1}$ और $\mathbf{F_2}$ दो मासों $m_{1}$ और $m_{2}$ के बीच रखा गया हो, जो स्थान $\mathbf{r_1}$ और $\mathbf{r_2}$ पर हैं, तो $F_1$ $=-F_2=-\frac{r_{12}}{r_{12}^{3}} G M_{O}^{2}\left(\frac{m_{1} m_{2}}{M_{0}^{2}}\right)^{n}$, जहां $M_{0}$ एक द्रव्यमान का आयाम वाला स्थिरांक है, $r_{12}=\mathbf{r_1}-\mathbf{r_2}$ है और $\mathrm{n}$ एक संख्या है। ऐसे मामले में,

(a) पृथ्वी पर गुरुत्वाकर्षण के कारण गति का अंतर विभिन्न वस्तुओं के लिए अलग होगा।

(b) केपलर के तीनों कानूनों में से कोई भी एक भी मान्य नहीं होगा।

(c) केवल तीसरे कानून अवैध हो जायेगा।

(d) $n$ नकारात्मक होने पर, जल से हल्का एक पदार्थ जल में डूब जायेगा।

उच्चारण 8.15 निम्नलिखित में से कौन से सत्य हैं?

(a) ध्रुवीय उपग्रह उत्तर-दक्षिण दिशा में पृथ्वी के चारों दिशाओं में घूमता है।

(b) भू-स्थिर उपग्रह पृथ्वी के चारों दिशाओं में पलटता है।

(c) भू-स्थिर उपग्रह पृथ्वी के पश्चिम-पूर्व दिशा में घूमता है।

(d) ध्रुवीय उपग्रह भू-स्थिर उपग्रह पृथ्वी के पूर्व-पश्चिम दिशा में घूमता है।

उच्चारण 8.16 पृथ्वी की सतह पर एक विस्तारित शरीर के केंद्र और उसका भू-गुरुत्व केंद्र

(a) हर आकार के शरीर के लिए हमेशा एक ही बिंदु पर होते हैं।

(b) केवल गोलकार शरीरों के लिए हमेशा एक ही बिंदु पर होते हैं।

(c) कभी-कभी एक ही बिंदु पर नहीं हो सकते।

(d) वस्तुएं, कहें उनके आकार $100 \mathrm{~m}$ से कम हों, के लिए आपस में नजदीक होते हैं।

(e) अगर वस्तु को पृथ्वी के गहराई में ले जाया जाता है तो दोनों बदल सकते हैं।

VSA

8.17 वायुमंडल में हवा के अणु भूमि की गुरुत्वाकर्षण शक्ति के द्वारा आकर्षित होते हैं। समझाइए कि क्यों सभी वे पृथ्वी में ऐसे ही नहीं गिरते हैं जैसे एक सेब पेड़ से नीचे गिरता है।

8.18 केंद्रीय बल और गैर-केंद्रीय बल के एक उदाहरण दीजिए।

8.19 मंगल ग्रह के लिए क्षेत्रीय वेग बनाम समय ग्राफ बनाइए।

8.20 सूर्य के चारों ओर पृथ्वी की क्षेत्रीय वेग की दिशा क्या होती है?

8.21 दो बिंदु मासों के बीच के स्थानवाला गुरुत्वाकर्षण बल जब वे एकत्रीकृत कर के पानी में समाए जाते हैं, तो इसका क्या प्रभाव होता है?

8.22 क्या किसी बॉडी को कार्यशीलता हो सकती है लेकिन भार नहीं हो सकता?

8.23 हम एक कन्डक्टर के अंदर एक चार्ज को विद्युत फील्डों से छिपा सकते हैं। क्या हम किसी वस्तु को निकटवर्ती पदार्थ के ग्रहणीय प्रभाव से कन्हों से चिपा सकते हैं या इससे दूसरे किसी तरीके से?

8.24 पृथ्वी के चारों ओर घूम रहे एक छोटे से अंतरिक्ष यान में स्थित एक अंतरिक्ष यात्री को गुरुत्वाकर्षण नहीं महसूस होता है। अगर पृथ्वी के चारों ओर घूम रहे एक बड़े साइज के अंतरिक्ष स्टेशन में वह क्या उम्मीद कर सकता है, कि वह गुरुत्वाकर्षण को महसूस कर पाएगा?

8.25 एक खोखली गोलीय गोलाकार पतली परत (रेज़ायुस) (असंतुलित घनत्व वाली) और एक बिंदु मास के बीच के गुरुत्वाकर्षण बल $F$ होता है। $r$ वे बिंदु के दूरी है जो गोलीय गोलकार शक्ति के केंद्र से होती है। $F$ बनाम $r$ के ग्राफ की प्रकृति दिखाएं जहां $r$ गोलीय गोलकार पतली के केंद्र से दूरी है।

8.26 आपहेलियन और पेरिहेलियन में से पृथ्वी की गति कहाँ अधिक होती है और क्यों?

8.27 इक्वेटोरियल तल और थांबोपकारी उपग्रह के आकारीय क्षेत्र (ऑर्बिटल प्लेन) के बीच का कोण क्या होता है?

SA

8.28 औसत सौर दिवस सूर्य द्वारा ज़ेनिथ बिंदु (मेरिडियन) से गुजरने पर दो संवर्धन के बीच समय अंतर होता है।

नक्षीय दिवस दूर सितारे द्वारा ज़ेनिथ बिंदु (मेरिडियन) के माध्यम से दो लगातार गुजरिशों के बीच का समय अंतर होता है।

उचित डायग्राम द्वारा धरती के स्पिन और कक्षीय गति को दिखाकर दिखाएं कि औसत सौर दिवस सिद्धांतिक दिवस से चार मिनट लंबा होता है। दूसरे शब्दों में, दूर के सितारे हर लगातार दिन 4 मिनट पहले उगेंगे।

(संकेत: आप धरती के लिए वृत्ताकार कक्ष का मान ले सकते हैं)।

8.29 दो एक जैसे भारी गोल मंडलों की दूरी उनके त्रिज्या की 10 गुणा है। क्या उनके केंद्रों को जोड़ने वाली रेखा के मध्यवर्ती स्थान पर रखा गया वस्त्र स्थिर संतुलन या अस्थिर संतुलन में होगा? अपने उत्तर के लिए कारण बताएँ।

8.30 पृथ्वी के चारोंओर सेटेलाइट के लिए निम्नलिखित ग्राफ का स्वरूप दिखाएं।

(ए) जैंत्रिक कोण $र$ के बनाम केंद्रबिंदु की ऊर्जा $के$

(बी) जैंत्रिक कोण $र$ के बनाम केंद्रबिंदु की संभवनीय ऊर्जा $यू$

(सी) जैंत्रिक कोण $र$ के बनाम केंद्रबिंदु की कुल ऊर्जा $व$।

8.31 कुछ कर्व (चित्र 8.2) दिखाए गए हैं। समझाएं कि कौन से कर्व एक प्रक्षेपी के द्वारा भ्रामण के द्वारा जोड़े गए नियमों के अनुसार संभव हो सकते हैं (हवा की घर्षण को अनदेखा करें)।

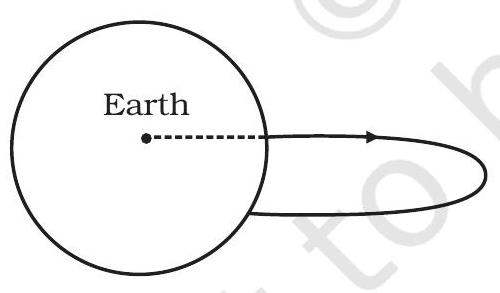
(ए)

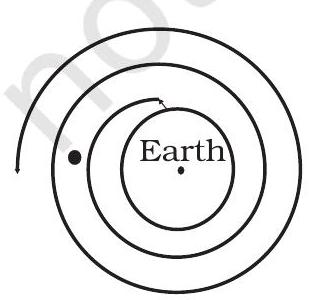
(ड)

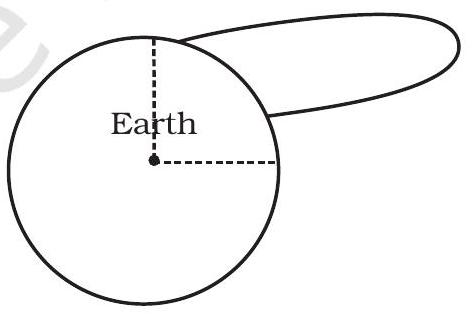
(ब)

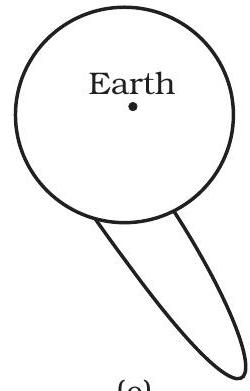
(इ)

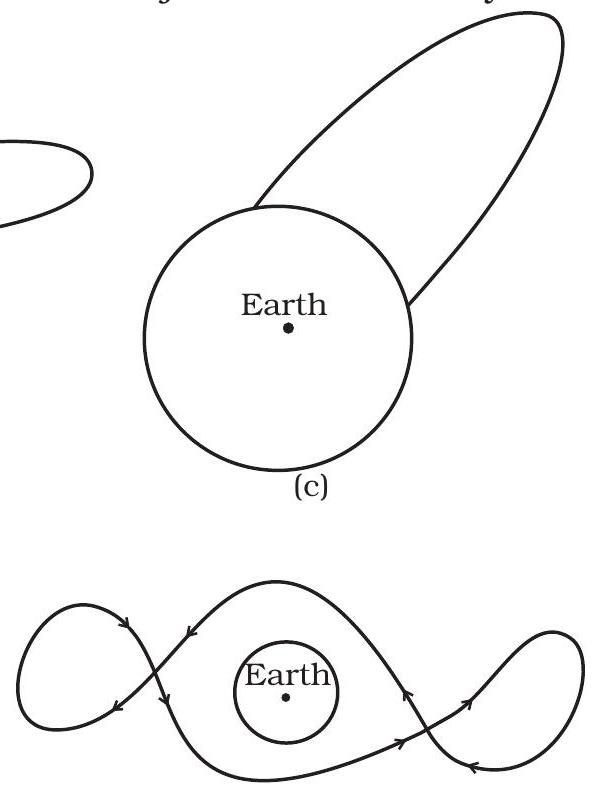
(फ)

चित्र 8.2

8.32 एक पदार्थ का भार $m$ धरती की सतह से उठाया जाता है और इसकी उचाई धरती के केंद्र से दूरी के बराबर होती है, अर्थात्, यह धरती के केंद्र से $R$ से $2 R$ दूर ले जाता है। इसकी संभावनीय ऊर्जा में बदलाव क्या होगा?

8.33 एक मास $m$ को अंतःस्थ मध्यवर्ती $O$ के माध्यम से एक पतली वृत्ताकार छल्ली पर माध्यम बनाया जाता है और इसकी त्रिज्या $M$ और त्रिज्या के आपसी संबंध $r$ (चित्र. 8.3) है।

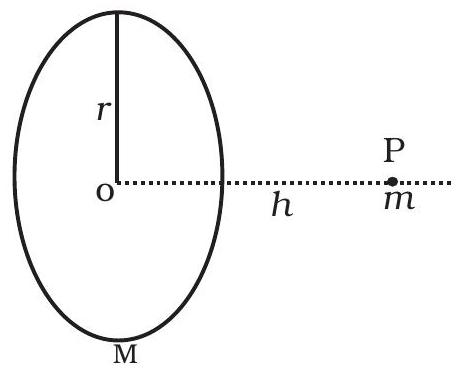
चित्र 8.3

यदि मास को और भी दूर हटाया जाता है जिससे प्रामाणिक बनाने वाली धरती की त्रिज्या $2 h$ हो जाती है, तो अभिकर्षण की शक्ति के किस गुणकार द्वारा घट जाएगा, यदि $h=r$ हो ?

LA 8.34 एक सूरज की तरह एक तारा के आस-पास कई शरीर हैं जो विभिन्न दूरी में घूम रहे हैं। मान लीजिए कि वे सभी वृत्ताकार गतियों में घूम रहे हैं। $r$ शरीर की दूरी से सेंटर तक हो और इसकी रैखिक वेग $ v $, कोणीय वेग $ \omega $, कीनेटिक ऊर्जा $ K $, गुरुत्वाकर्षणी बहुगुणक ऊर्जा $ U $, कुल ऊर्जा $ E $ और कोणीय मामला $ l $ हो। जब वृत्ताकार की दूरी $ r $ बढ़ती है, तो उपरोक्त मात्राएं बढ़ती या कम होती हैं।

8.35 एक समान कोने के चारों कोनों पर एम मास के छह बिंदु मान हैं जो एल लम्बाई के एक नियमित षट्कोण के कोनों पर होते हैं। किसी भी बिंदु पर बल की गणना करें।

8.36 एक उपग्रह को धरती के परिधि-कक्ष में स्थिति वर्तमान संचार के लिए भेजा जाना है।

(अ) ऐसे एक उपग्रह की ऊचाई की गणना करें।

(ब) जन्म पट्टी पर शून्य से प्रकाशित एक बिंदु के किसी भी स्थान से कम से कम एक उपग्रह की आवश्यकता परिणामी कम से कम संख्या निकालो जिसे धरती के पूरे भूमध्य रेखा से एक उपग्रह दिखाई देता हो।

$\left[M=6 \times 10^{24} \text{~kg}, R=6400 \text{~km}, T=24 \text{~h}, \text{G}=6.67 \times 10^{-11}\right.$ SI इकाईयां $]$

8.37 धरती का वृत्ताकार मार्ग k बीजों से ऊँचाई 0.0167 है। इस प्रकार, सूरज से धरती की दूरी और जब धरती सूरज के चारों ओर घूमती है तो इसकी गति दिन-प्रतिदिन बदलती है। इसका मतलब है कि वार्षिक दिन की लंबाई बदलती है। मान लें कि धरती का घूम धनुष्वाकार मध्यस्थ अक्ष के लंबकोणी है और सबसे छोटा और सबसे लंबा दिन का लंबाई पता करो। एक दिन को दोपहर से दोपहर तक लेना चाहिए। क्या यह साल के दौरान दिन की लंबाई के विविधता का समाधान करता है?

8.38 एक उपग्रह धरती के चारों में वृत्ताकार विपरीतपथ में है जिसकी अष्टमी 6 R और समांतरी 2 R है जहां R=6400 \text{~km} धरती का त्रिज्या है। प्रकाशांकविता की गणना करें। अपोगी और पेरिजी पर उपग्रह की वेग निकालें। इस उपग्रह को समांतरी वृत्ताकार में नकली किया जाना चाहिए अगर ऐसा करना होता है तो क्या करना चाहिए?

$\left[\text{G}=6.67 \times 10^{-11}\right.$ SI इकाईयां और $\left.M=6 \times 10^{24} \text{~kg}\right]$

8.24 हाँ, अगर अंतरिक्ष जहाज का आकार पर्याप्त बड़ा होता है ताकि वह $g$ में बदलाव का पता लगा सके।

8.25

8.26 अड़ी ऊर्जा को स्थिर रखने के लिए पृथ्वी को अधिक रेखांकन दूरी तय करनी पड़ती है, पेरिहेलियन में।

8.27 $\begin{array}{ll}\text { (क) } 90^{\circ} & \text { (ख) } 0^{\circ}\end{array}$

8.28 हर दिन पृथ्वी एक अंतरिक्ष में करीब $1^{\circ}$ की प्रगति करती है। तब, इसे $361^{\circ}$ (जिसे हम 1 दिन के रूप में परिभाषित करते हैं) के लिए घूरना होगा कि सूर्य फिर से ज्योति के बिंदु पर हो। क्योंकि $361^{\circ}$ 24 घंटों के बराबर है; अतिरिक्त $1^{\circ}$ के बराबर लगभग 4 मिनट [3 मिनट 59 सेकंड] होते हैं।

8.29 मध्य में स्थिति मास को थोड़ी सी दूरी $h$ दायाँ में चलने के माध्यम से ले जाने पर, उस पर लगने वाले बल हैं: दाएँ $\frac{\mathrm{GMm}}{(R-h)^{2}}$ और बाएँ $\frac{G M m}{(R+h)^{2}}$। पहला दूसरे से अधिक है। इसलिए, नेट बल भी दाईं ओर होगा। इसलिए, संतुलन अस्थिर होगा।

8.30

8.31 पृथ्वी की गुरुत्वाकर्षण बल के तहत किसी तत्व का चाल क्रम एक पराबोलीय खंड (पृथ्वी के बाहरी क्रिया के लिए) होगा, जिसमें पृथ्वी का केंद्र एक फोकस होगा। केवल (क) इस आवश्यकता को पूरा करता है।

उदाहरण समस्याएं-भौतिकी

8.32 $\mathrm{mgR} / 2$।

8.33 केवल यानि $m$ और $O$ के बीची रेखा के लिए समापन के लिए लगने वाले बल के केवल क्षैतिज घटक सही बदलते हैं। युक्तियां:

$\left[\frac{2 r}{\left(4 r^{2}+r^{2}\right)^{3 / 2}}\right]\left[\frac{\mu}{\left(r^{2}+r^{2}\right)^{3 / 2}}\right]$

$=\frac{4 \sqrt{2}}{5 \sqrt{5}}$।

8.34 जब $r$ बढ़ता है:

$U\left(=-\frac{G M m}{r}\right)$ बढ़ता है।

$v_{c}\left(=\sqrt{\frac{G M}{r}}\right)$ कम होता है।

$\omega\left(=\frac{v_{c}}{r} \times \frac{1}{r^{3 / 2}}\right)$ कम होता है।

$K$ कम होता है क्योंकि $v$ बढ़ता है।

$E$ बढ़ता है क्योंकि $|U|=2 \mathrm{~K}$ और $U<\mathrm{O}$.

$l$ बढ़ता है क्योंकि $m v r \propto \sqrt{r}$।

8.35 इस समस्या के अनुसार:

$\mathrm{AB}=\mathrm{C}$

$(\mathrm{AC})=2 \mathrm{AG}=2 \cdot l \cdot \frac{\sqrt{3}}{2}=\sqrt{3} l$

$\mathrm{AD}=\mathrm{AH}+\mathrm{HJ}+\mathrm{JD}$

$=\frac{l}{2}+l+\frac{l}{2}$

$=21$.

$A E=A C=\sqrt{3} l, \mathrm{AF}=l$

$m$ के कारण $\mathrm{F}$ और $\mathrm{B}$ पर $\mathrm{AD}$ दिशा का बल

$=G m^{2}\left[\frac{1}{l^{2}}\right] \frac{1}{2}+G m^{2}\left[\frac{1}{l^{2}}\right] \frac{1}{2}=\frac{G m^{2}}{l^{2}}$

$\mathrm{E}$ और $\mathrm{C}$ पर मास के कारण $\mathrm{AD}$ दिशा का बल

उस लेख की हिंदी संस्करण से
$= G m^{2} \frac{1}{3 l^{2}} \cos (30)+\frac{G m^{2}}{3 l^{2}} \cos \left(30^{\circ}\right)$ $=\frac{G m^{2}}{3 l^{2}} \sqrt{3}=\frac{G m^{2}}{\sqrt{3} l^{2}}$.

माल $M$ के कारण द्वार D पर बल

$=\frac{G m^{2}}{4 l^{2}}$.

$\therefore$ कुल बल $=\frac{G m^{2}}{l^{2}}\left[1+\frac{1}{\sqrt{3}}+\frac{1}{4}\right]$.

8.36 (क) $r=\left(\frac{G M T^{2}}{4 \pi^{2}}\right)^{1 / 3}$

$$ \begin{aligned} \therefore h & =\frac{G M T^{2}}{4 \pi^{2}}{ }^{1 / 3}-R \ & =4.23 \times 10^{7}-6.4 \times 10^{6} \ & =3.59 \times 10^{7} \mathrm{~m} . \end{aligned} $$

(ख) $\theta=\cos ^{-1} \frac{R}{R+h}$

$$ \begin{aligned} & =\cos ^{-1} \frac{1}{1+h / r} \ & =\cos ^{-1} \frac{1}{1+5.61} \end{aligned} $$

$$ =81^{\circ} 18^{\prime} $$

$\therefore 2 \theta=162^{\circ} 36^{\prime}$

$\frac{360^{\circ}}{2 \theta} \approx 2.21 ;$ हेंस एक न्यूनतम संख्या $=3$।

8.37 कोणीय पल और क्षेत्रीय वेग सूर्य के परिक्रमण के दौरान लगातार हैं।

पेरीज पर $r_{p}^{2} \omega_{p}=r_{a}^{2} \omega_{a}$ एपोज पर।

यदि ’ $a$ ’ ध्रुवीय मुख्य धुरी है, तो $r_{p}=a(1-e)$ और $r_{a}=a(1+e)$।

$\therefore \frac{\omega_{p}}{\omega_{\mathrm{a}}}=\left(\frac{1+e}{1-e}\right)^{2}, e=0.0167$

$\therefore \frac{\omega_{\mathrm{p}}}{\omega_{\mathrm{a}}}=1.0691$

चलान कौशल $\omega$ है जो $\omega_{\mathrm{p}}$ और $\omega_{\mathrm{a}}$ की ज्यामिति मान है और यह मान ध्रुवीय सौर दिन को दर्शाता है,

$\therefore\left(\frac{\omega_{\mathrm{p}}}{\omega}\right)\left(\frac{\omega}{\omega_{\mathrm{a}}}\right)=1.0691$

$\therefore \frac{\omega_{\mathrm{p}}}{\omega}=\frac{\omega}{\omega_{\mathrm{a}}}=1.034$।

यदि $\omega$ का अर्थ $1^{\circ}$ प्रति दिन है

(औसत कोणीय स्पीड), तो

$\omega_{\mathrm{p}}=1.034$ प्रतिदिन और $\omega_{\mathrm{a}}=0.967$ प्रतिदिन। क्योंकि $361^{\circ}=14 \mathrm{hrs}$: औसत सौर दिन, हम पाते हैं 361.034 जो $24 \mathrm{hrs} 8.14$ " (8.1" लंबा) के हमारे होते हैं और $360.967^{\circ}$ जो $23 \mathrm{hrs} 59 \mathrm{~min} 52^{\prime \prime}$ (7.9" छोटा) के हमारे होते हैं।

इससे साल में दिन की लंबाई के वास्तविक परिवर्तन की व्याख्या नहीं होती।

8.38 $\quad r_{a}=a(1+e)=6 R$

$r_{p}=a(1-e)=2 R \quad \Rightarrow e=\frac{1}{2}$

क्षैतिजी मुहीम:

पीछे बाल का क्षैतिजी महीन के साथ ज्ञाष् प्राथ के क्षैतिज महीन

$\therefore m v_{p} r_{p}=m v_{a} r_{a}$

$\therefore \frac{v_{a}}{v_{p}}=\frac{1}{3}$।

परमाणु के अनुरूप मुहीन:

परामाणु पर पीछे बाल का ऊर्जा $=$ परामाणु पर आगामी ऊर्जा

$\frac{1}{2} m v_{p}^{2}-\frac{G M m}{r_{p}}=\frac{1}{2} m v_{a}^{2}-\frac{G M m}{r_{a}}$

$\therefore v_{p}^{2}\left(1-\frac{1}{9}\right)=-2 G M\left[\frac{1}{r_{a}}-\frac{1}{r_{p}}\right]=2 G M\left[\frac{1}{r_{a}}-\frac{1}{r_{p}}\right]$

वार्तालाप: $v_{p}=\frac{2 G M\left[\frac{1}{r_{p}}-\frac{1}{r_{a}}\right]^{1 / 2}}{\left[1-\left(v_{a} / v_{p}\right)\right]^{2}}=\left[\frac{\frac{2 G M}{R}\left[\frac{1}{2}-\frac{1}{6}\right]}{\left(1-\frac{1}{9}\right)}\right]^{1 / 2}$

$$ =\left(\frac{2 / 3}{8 / 9} \frac{G M}{R}\right)^{1 / 2}=\sqrt{\frac{3}{4} \frac{G M}{R}}=6.85 \mathrm{~km} / \mathrm{s} $$

$v_{p}=6.85 \mathrm{~km} / \mathrm{s} \quad, v_{a}=2.28 \mathrm{~km} / \mathrm{s}$.

जब $r=6 R$ हो, तो $v_{c}=\sqrt{\frac{G M}{6 R}}=3.23 \mathrm{~km} / \mathrm{s}$ होता है।

इसलिए, अपोजी पर एक परिपत्राकारी में स्थिति के लिए हमें वेग को $\Delta=(3.23-2.28)=0.95 \mathrm{~km} / \mathrm{s}$ से बढ़ाना होगा। इसको सही ढंग से उपयुक्त रॉकेट्स द्वारा ईंधन को देने द्वारा किया जा सकता है।