अध्याय 7: कण एवं घुमावी गति की प्रणाली (Adhyay 7: Kan evam Ghumavi Gati Ki Pranali)
अध्याय 7
अवयव और घूर्णनीय गति
MCQ I
7.1 निम्नलिखित में से किसके केंद्रीय मांस शरीर के बाहर होता है?
(a) एक पेंसिल
(b) एक शॉटपट
(c) एक पासा
(d) एक बांगड़ी
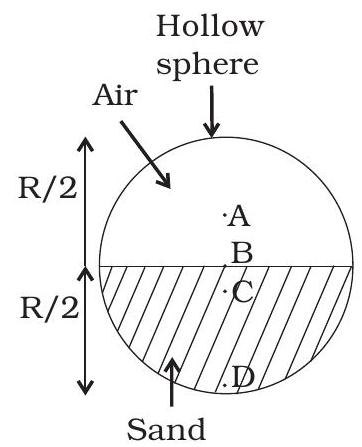
7.2 चित्र 7.1 में दिखाए गए प्रणाली के केंद्रीय कम का संभावित स्थान कौन सा हो सकता है?
(a) $\mathrm{A}$
(b) $\mathrm{B}$
(c) $\mathrm{C}$
(d) $\mathrm{D}$
7.3 एक वस्तु जिसकी भार $m$ है, यह $y z$-इभाद में एक समान वेग $v$ के साथ गतिशील है जिसका प्राजेक्टरी +ve $y$-क्षैतिज पराधीयक ध्रुव से टकराई जाती है
चित्र 7.1
और $y=$ का एक स्थानांतरित जीवनशैली पट्टि पर लज्जीतर डबलों से जोरदार वार्तमान्याच्या रूप में आईटम से जूंग होते हैं, यह उसके मौजूदा मैक्सोर्स पॅतटा में अपना गतिविधि का परिवर्तन है:
(a) $m v a \hat{\mathbf{e}}_{x}$
(b) $2 m v a \hat{\mathbf{e}}_{x}$
(c) $y m v \hat{\mathbf{e}}_{x}$
(d) $2 y m v \hat{\mathbf{e}}_{x}$
7.4 जब एक डिस्क समान घूर्णणीय कोणीय वेग के साथ घूर्णित होता है, तो निम्नलिखित में से कौन सा सत्य नहीं है?
(a) घूमने की चाल का हवा रहती है।
(b) घूर्णनी के ध्रुव की ओरियंटेशन रहती है।
(c) घूर्णन की गति गैर-शून्य होती है और रहती है।
(d) कोणीय तेजी गैर-शून्य होती है और रहती है।
7.5 एक समान वर्गाकार प्लेट में से एक कसबर्ढ़ हिस्सा $Q$ निकला हुआ है और प्लेट के केंद्र पर चिपकाया गया है जिससे पीछे एक छेद बचा है (चित्र 7.3)। केंद्रीय मांस तकति परिपटी तब

चित्र 7.3
(a) बढ़ा हुआ
(b) कम हुआ
(c) वही
(d) अप्रत्याशित तरीके से बदल गया।
7.6 समस्या 7.5 में, प्लेट का आंतर्रष्ट्री CM अब $x$-$y$-तल इम्र चतुर्थ क्षेत्र में है,
(a) I
(b) II
(c) III
(d) IV
7.7 एक गैर-सम-मिश्रित रॉड का घनत्व लंबाई $1 \mathrm{~m}$ में $\rho(x)=a\left(1+b x^{2}\right)$ द्वारा फहा गया गया है
जहां $\mathrm{a}$ और $\mathrm{b}$ स्थाई हैं और $o \leq x \leq 1$।
रॉड का केंद्र शिरोमांस पर होगा
(a) $\frac{3(2+b)}{4(3+b)}$
(b) $\frac{4(2+b)}{3(3+b)}$
(c) $\frac{3(3+b)}{4(2+b)}$
(d) $\frac{4(3+b)}{3(2+b)}$
7.8 एक मेरी-मेरी-गो-आराउंड, जिसमें एक छक्का-जैसा प्लेटफॉर्म और माप $\mathrm{R}$ और भार $\mathrm{M}$ का है, वाह घूर्णनी के साथ घूम रहा है। एक व्यक्ति का भार M उस पर खड़ा है। एक अवस्था में, व्यक्ति छक्के से केंद्र की ओर के समानांतर रेंखीय बाहर उछालता है (चक्रदीर्घता की दृष्टी से देखें)। चक्र की गति उसके बाद
(a) $2 \omega$
(b) $\omega$
(c) $\frac{\omega}{2}$
(d) 0
MCQ II
7.9 सही विकल्प चुनें:
जूलें और लघुवृत्तीय गति के लिए, कोणीय प्रस्तीर्णता $\mathbf{L}$ और कोणीय वेग $\boldsymbol{\omega}$ दोनों सामर्थ्य के लिए समानांतर नहीं होना चाहिए।
(b) एक स्थिर अक्ष के चारोंओर घुमाव के लिए, कोणीय प्रस्तीर्णता $\mathbf{L}$ और कोणीय वेग $\boldsymbol{\omega}$ हमेशा सामर्थ्य के लिए समानांतर होते हैं।
(c) एक सामान्य स्थलानुक्रमिक गति के लिए, प्राप्ति $\mathbf{p}$ और वेग $\mathbf{v}$ हमेशा सामर्थ्य के लिए समानांतर होते हैं।
(d) एक सामान्य स्थलानुक्रमिक गति के लिए, त्वरण a और वेग $\mathbf{v}$ हमेशा सामर्थ्य के लिए समानांतर होते हैं।
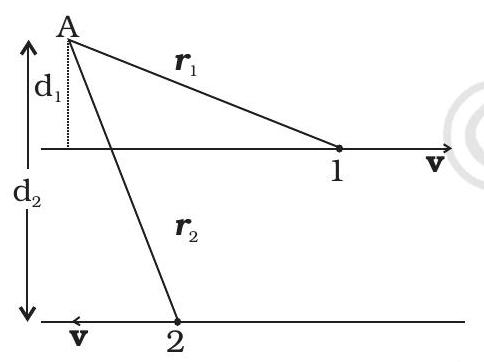
7.10 चित्र 7.5 में दिखाया गया है कि दो एक ही भारमान अणु 1 और 2 हैं, प्रत्येक मास $म$ के, समान तथा समानवेग $\mathbf{v}$ के अभिलक्ष्य रेखाओं के साथ परस्पर विपरीत दिशा में चलते हैं। एक विशेष समय पर, $\mathbf{r_1}$ और $\mathbf{r_2}$ पॉइंट $ए$ से बनाए गए उनके संबंधीय स्थान वेक्टर हैं जो परिलक्षित रेखाओं के ताले में होता है। सही विकल्प चुनें:
चित्र 7.4
(a) बिनवक्री अणु 1 की कोणीय प्रस्तीर्णता $\boldsymbol{l_1}$ एकाग्रक $\mathrm{A}$ के बारे में $\boldsymbol{l_1}=\operatorname{म्वड}_{1}$ है।
(b) बिनवक्री अणु 2 की कोणीय प्रस्तीर्णता $\boldsymbol{l_2}$ एकाग्रक $\mathrm{A}$ के बारे में $\boldsymbol{l_2}=\mathbf{म व r}_{2}$ है।
(c) एक सिस्टम की उपस्थिति की कोणीय प्रस्तीर्णता $\boldsymbol{l}$ पर A के बारे में $\boldsymbol{l}=म व\left(\boldsymbol{r_1}+\boldsymbol{r_2}\right)$ है।
(d) एक सिस्टम की उपस्थिति की कोणीय प्रस्तीर्णता $\boldsymbol{l}$ पर A के बारे में $\boldsymbol{l}=म व\left(d_{2}-d_{1}\right) \otimes$ होती है।
एक पृष्ठ से बाहर जाने वाला एकक वेक्टर दर्शाता है।
एक पृष्ठ में चलने वाला एकक वेक्टर दर्शाता है।
7.11 किसी प्रणाली के भोज बाह्य टॉर्क $0$ आक्ष के बारे में होता है। निम्नलिखित में से कौन से मेल खाने वाले हैं?
(a) बल अक्षस्थल से उपयोग पर लागू हो सकते हैं।
(b) बल घुमाव के अक्ष पर कार्रवाई कर सकते हैं।
(c) बल घुमाव के अक्ष के समानांतर हो सकते हैं।
(d) कुछ बलों द्वारा प्रकाशित टॉर्क और अन्य बलों द्वारा प्रकाशित टॉर्क के समान और विपरीत हो सकते हैं।
अणुओं के प्रणाली और कोणीय गति
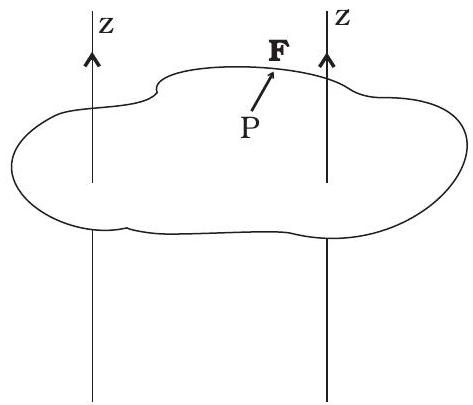
7.12 प्रणाली में एक लैमिना का आकार दिखाती है $x-y$ समतल में। $z$ और $z’$ अक्ष उसके ताले के खंड में सीधे होते हैं। बिन में एक बल $\mathbf{F}$ बुनियादी स्थान $\mathrm{P}$ पर समाता है, जैसा कि दिखाया जाता है। निम्नलिखित में से कौन से सत्य हैं? (बिना के निकट ज़ै. अक्ष। प्राकृतिक करीन ने $\mathrm{z}$- अक्ष से अधिकतम बल लगाया।)
चित्र 7.5
(a) $\mathbf{F}$ द्वारा $z$- अक्ष के बारे में उत्पन्न टॉर्क $\tau$ कद्रीभूत $-\hat{\mathbf{k}}$ के अनुरूप है।
(b) $\mathbf{F}$ द्वारा $z’$- अक्ष के बारे में उत्पन्न टॉर्क $\tau’$ कद्रीभूत $-\hat{\mathbf{k}}$ के अनुरूप है।
(c) $\mathbf{F}$ द्वारा $z$- अक्ष के बारे में उत्पन्न टॉर्क $\tau$ मान में अधिक है जो $z$- अक्ष के बारे में होता है।
(d) कुल टॉर्क $\tau=\tau+\tau’$ दिया जाता है।
7.13 किनारों $a$ और भार $m$ वाली एक क्यूब के चित्र 7.6 में संदर्भित हो रहा है, सत्य या असत्य बताओं। ($\mathrm{O}$ संचारिका केंद्र है।)

Fig. 7.6
(a) क्यूब के चंद्रमा अक्ष के बारे में निर्मोम अक्ष का पलट अंश $I_{z}=I_{x}+I_{y}$ है
(b) क्यूब के चंद्रमा अक्ष (के बारे में निर्मोम अक्ष का पलट अंश) है
$$ I_{z}^{\prime}=I_{z}+\frac{m a^{2}}{2} $$
(c) क्यूब के चंद्रमा के बारे में इनर्टिया बीना अक्ष (के बारे में निर्मोम अक्ष का पलट अंश) है
$$ =I_{z}+\frac{m a^{2}}{2} $$
(d) $I_{x}=I_{y}$
VSA
7.14 एक प्रभागीय खण्ड पृथ्वी पर किसी शरीर का केंद्र भार का केंद्र से मेल खाता है जबकि एक “विस्तारित” शरीर के लिए ऐसा हो सकता है नहीं। इसके संबंध में ‘छोटा’ और ‘विस्तारित’ का गुणात्मक अर्थ क्या है?
निम्नलिखित में कौन सा दोनों मेल खाता है? एक इमारत, एक तालाब, एक झील, एक पहाड़?
7.15 एक ठोस गोला एक खोखली सिलिंडर की तुलना में समान भार और ऊर्ध्वकेंद्र से होने के कारण रोचक का कमतरता रखता है?
7.16 एक पलटी हुई कठोर शरीर के एक बिंदु की कोणीय स्थिति $\theta$, समय $t$ के साथ में दिखाई देती है, जैसा कि चित्र 7.7 में दिखाया गया है। क्या शरीर घड़ी की दिशाओं में घुम रहा है या उल्टी दिशा में?

चित्र 7.7
7.17 एक सामान्य क्यूब का भार $m$ और ओर $a$ वाली फ्रिक्शन-मुक्त समतल सतह पर रखा गया है। चित्र 7.8 में दिखाया गया हुआ हैः

चित्र 7.8
निम्नलिखित को मिलाओ (सबसे उपयुक्त विकल्प):
| पट्टी I | पट्टी II |
|---|---|
| (a) $m g / 4<F<m g / 2$ | (i) क्यूब ऊपर चलेगा |
| (b) $F>m g / 2$ | (ii) क्यूब गति का निर्दिष्ट नहीं |
| (c) $F>m g$ | (iii) क्यूब A पर घूमने और स्लिप करने लगेगा |
| (d) $F=m g / 4$ | (iv) सामान्य प्रतिक्रिया का प्रभाव A से $a / 3$ दूर, कोई गति नहीं। |
7.18 एक सामान्य गोला भार $m$ और त्रिज्या $R$ वाली एक घूर्णनशील सतह पर रखा गया है (चित्र 7.9)। गोला को ऊंचाई $h$ से जमीन पर मारा जाता है। निम्नलिखित को मिलाओ:

चित्र 7.9
| पट्टी I | पट्टी II |
|---|---|
| (a) $h=R / 2$ | (i) गोला बिना स्लिपिंग के स्थिर गति और कोई ऊर्जा हानि के साथ घूमता है |
| (b) $h=R$ | (ii) गोला घूड़ देता है, घर्षण से ऊर्जा हानि होती है |
| (सी) ह = ३ आर / २ | (त्) गोला घूमता है, घर्षणा के कारण उसकी ऊर्जा हानि होती है। | | (डी) ह = ७ आर / ५ | (थ) गोला के पास केवल स्थानांतरणीय गति होती है, घर्षणा के कारण उसकी ऊर्जा हानि होती है। |
७.१९ एक अचिह्नियों का समूह के एक ठोस शरीर पर कार्यरत गैर-लगभगी बलों का वेक्टर योग गैर-शून्य दिया गया है। यदि किसी निश्चित बिंदु के लिए उन बालों के कारण समूह के सभी टोर्कों का वेक्टर योग शून्य पाया जाता है, क्या यह यह अपेक्षित होता है कि इसका कोई भी अनुकूल बिंदु शून्य होता है?
७.२० एक अक्षर के ऊपर यूनिफॉर्म गति में एक पहिया, जो उसके केंद्र से गुजरने वाले एक अक्ष के माध्यम से पास होती है और उसके तस्वीर के ऊतकों पर ऐसी है उसके ठोस (स्थानांतरणीय सहित क्रोशित) संतुलन में मानसिक तृप्ति में मानी जाती है चूंकि इसकी गति बनाए रखने के लिए कोई नेट बाह्य बल या टोर्क आवश्यक नहीं होता है। हालांकि, पहिये के घटक कणों को केंद्र की ओर संरेख माध्यम से एक केंद्रीय तत्वाकर्षणीय त्वरण का अनुभव होता है। आप इस तथ्य को पहिया संतुलित होने के साथ कैसे सुलझाएँगे?
क्या आप एक आधे पहिये को पहिये के ठोस के केंद्र और उसके तस्वीर के उतक के आक्षण के लिए एक अच्छी गति में स्थापित करने की आवश्यकता होगी? क्या आपको बाह्य बलों की आवश्यकता होगी उस गति को बनाए रखने के लिए?
७.२१ एक दरवाजा एक सिरे से पंखे हुए है और एक लंबवत धुरी के चारों ओर मुक्त है (चित्र 7.10)। क्या इस धुरी के इस धुरी के चारों ओर कोई भी टोर्क होता है? अपने उत्तर के लिए कारण दें।
७.२२ (एन-१) बराबर बिन्दु माल की हरी उत्पाद के सभी बिंदु मास्य के PSGHDI माध्यम से रखे जाते हैं। खाली बिंदु केंद्राबद्ध के उपर निर्माणित एक प्रारंभिक नियतन वेक्टर रहित होता है। केंद्रीय भार का स्थानीय मास्यीकरण वेक्टर ढूँढें।
प्रतिशत
७.२३ एक एकदम नियमित (क) अर्ध-वृत्त, (ख) चतुर्थ-वृत्त केंद्र पर मास्य का केंद्र ढूँढें।
७.२४ दो मोमेंट ऑफ इंर्शिया $I_{1}$ और $I_{2}$ के दो पिस्कवाद पास लाए गए हैं ($I_{1}$ समद्विक्न और केंद्र से गुजरने वाले अक्षों के बाहर, $I_{2}$ कोणीय त्रांसरण और केंद्र से पारित अक्षों के बाहर), और इसके साथ अपने धनात्मक वेगों के साथ घुम रहे हैं, अथवा एक-दूसरे से मिलते हैं।
(क) क्या प्रतिरक्षण के आणविक संरक्षण का नियम इस स्थिति में लागू होता है? क्यों?
(ख) दो-पिस्क संयंत्र की आणविक गति की त्वरण खोई जाती है।
(ग) प्रक्रिया में ऊर्जा की हानि की गणना करें
(घ) इस हानि का कारण बताएं।
७.२५ एक नपुंसकता के आयतनयों द्वारा दिए जा रही है कि एक आयाम तेजीवाल घोल एक आयतन के सापेक्ष अक्ष के बारे में घूम रहा है। यह एक गति में आयं क्या करता है?
एक पहिया $र$ के तेजी से $\omega_{o}$ अक्ष के आसपास एक समतलीय माध्यम पर प्रवेश करता है। गतिशील घर्षणात्मक त्वरण $\mu_{k}$ है।
(क) इसे टेबल के संपर्क में लाने से पहले केंद्र मात्रा की गति क्या थी?
(ख) पेंच की धरा पर संपर्क में आने पर उसके पिंड की रैम की तेजीं वेग क्या होती है?
(का) वस्त्रीय तत्व के समय संपर्क में आने पर, केंद्र मात्रा की रैम की तेजी वेग में क्या होता है?
(ड) (बी) और (गा) में कौन सी शक्ति प्रभावित होती है?
(ए) घुमने के लिए शर्त क्या होनी चाहिए?
(फ) घूमना शुरू होने में लगने वाला समय का लाभेदार कीजिए।
7.26 दो आयतात्मक होलों वाले ड्रम जिनका त्रिज्या $R$ और $2R$ है, और एक ही ऊचाई $h$ है, वे घूम रहे हैं जिनकी आंगुलर वेग $\omega$ (घड़ी की उर्द्धा दिशा में) और $\omega$ (घड़ी के दिशा में) है। उनके मांधत्वक धुराओं, जो ठोस हैं स्थिर हैंऔर एकत्रित में एक आंतरिक तट से अलग हैं,$(3 R+\delta)$। वे अब संपर्क में लाए गए हैं$(\delta \rightarrow 0)$।
(ए) संपर्क के فورا बाद इंटरनाल बल को दिखाएँ।
(ब) संपर्क के فورा बाद इंटरनाल बाल और टॉर्क्क्स का पहचान करें।
(सी) जब घर्षण समाप्त हो जाता है तो चक्रीय वेगों के अन्तिम अनुपात क्या होगा?
उदाहरण प्रश्न-भौतिक विज्ञान
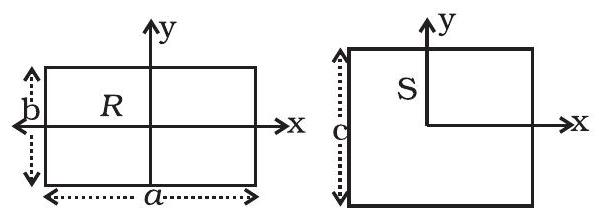
7.27 एक वर्गमय उंचा प्लेट $\mathrm{S}$ (पक्ष $\mathrm{c}$) और एक आयताकार वर्गमय प्लेट $\mathrm{R}$ (पक्ष b, पक्ष b) की छूट गुणकारी और भार होते हैं (चित्र 7.11)।
चित्र 7.11
दिखाएं कि
(i) $I_{x R} / I_{x S}<1$;
(ii) $I_{y R} / I_{y S}>1$;
(iii) $I_{z R} / I_{z S}>1$.
7.28 त्रिज्या $R$ वाला एक समान्तर वृत्त, अपने धा
7.19 No. दिया गया है $\sum_{i} \mathbf{F}_{i} \neq 0$
केवल एक निश्चित बिंदु ‘0’ के चारों तरफ़ घूमण कोणों के लिए यह सही होगा
$\sum_i \mathbf{r_i} \times \mathbf{F_i}=0$
किसी अन्य बिंदु $\mathrm{O}^{\prime}$ के चारों तरफ़ घूमण कोणों के लिए,
$\sum_i\left(\mathbf{r_i}-\mathbf{a}\right) \times \mathbf{F_i}=\sum_i \mathbf{r_i} \times \mathbf{F_i}-\mathbf{a} \times \sum_i F_i$
यहाँ, दूसरा सम्प्रेषण नहीं बना होगा।
7.20 में एक व्हील में सेंट्रीपिटल त्वरण आंतरिक
(a) शून्य (b) कम होता है (c) बढ़ता है (d) घर्षण (e) $v_{c m}=R \omega$।
(f) घर्षण के केंद्र मांस में उत्पन्न त्वरण:
$$ a_{c m}=\frac{F}{m}=\frac{\mu_{k} m g}{m}=\mu_{k} g $$
घर्षण के कारण मोमेंटीय त्वरण,
$$ \begin{aligned} & \alpha=\frac{\tau}{I}=\frac{\mu_{k} m g R}{I} \ & \therefore v_{c m}=u_{c m}+a_{c m} t \Rightarrow v_{c m}=\mu_{k} g t \ & \text { और } \omega=\omega_{o}+\alpha t \Rightarrow \omega=\omega_{o}-\frac{\mu_{k} m g R}{I} t \end{aligned} $$
सट्टे के बिना रोलिंग के लिए,
$$ \begin{aligned} & \frac{v_{c m}}{R}=\omega_{o}-\frac{\mu_{K} m g R}{I} t \ & \frac{\mu_{K} g t}{R}=\omega_{O}-\frac{\mu_{K} m g R}{I} t \end{aligned} $$
$$ t=\frac{R \omega_{o}}{\mu_{k} g\left(1+\frac{m R^{2}}{I}\right)} $$
7.26
(a)

$\mathbf{F} \uparrow$ पांवथडी वर बायांच्या अॅक्षीला बाळगणारे बाजू
$\mathbf{F} \downarrow$ पांवथडी वर उजव्या अॅक्षीला बाळगणारे बाजू (b) $\quad F^{\prime}=F=F^{\prime \prime}$ त्याच्या मदतगीतल्या आधारावर $F$ आणि $F^{\prime \prime}$ एकसारखे ताण असलेले एकत्रबंद चारधारा. $\mathrm{F}_{\text {net }}=0$
बाणासन प्रतिरोध $=F \times 3 R$, उल्हासा.
(c) गरज लागल्यास $\omega_{1}$ आणि $\omega_{2}$ अन्तिम कोणच्या वेगमानस्थिती (मालध्वनीच्या उल्हासी आणि डावी)

अंततः कोणतीही घर्षण नसतील.
म्हणजे, $R \omega_{1}=2 R \omega_{2} \Rightarrow \frac{\omega_{1}}{\omega_{2}}=2$
7.27 (i) चौघडयाच्या क्षेत्रफळास सामी चौघड्यानंतरित्या क्षेत्रफळ $=$ सतंब चौघड्याच्या क्षेत्रफळ $\Rightarrow c^{2}=a b$
$$ \frac{I_{x R}}{I_{x S}} \times \frac{I_{y R}}{I_{y S}}=\frac{b^{2}}{c^{2}} \times \frac{a^{2}}{c^{2}}=\left(\frac{a b}{c^{2}}\right)^{2}=1 $$
(i) आणि (ii) $\quad \frac{I_{y R}}{I_{y S}}>\frac{I_{x R}}{I_{x S}} \Rightarrow \frac{I_{y R}}{I_{y S}}>1$ आणि $\frac{I_{x R}}{I_{x S}}<1$.
(iii)
$$ \begin{aligned} & I_{z r}-I_{Z S} \propto\left(a^{2}+b^{2}-2 c^{2}\right) \ & =a^{2}+b^{2}-2 a b>0 \ \therefore & \left(I_{z R}-I_{z S}\right)>0 \ \therefore & \frac{I_{z R}}{I_{z S}}>1 . \end{aligned} $$
7.28 ऐनंदुलन कोणवेळीने केंद्र मानाची इंधनीवेळ असेल ’ $a$ ’ असा म्हणजे
$M a=F-f$
चक्राचं ऐनंदुलन ऐच्छिक कोनाचं आंतरिवेग असो $\alpha=a / R$. (रंगा नसल्यास)
तर
$$ \begin{align*} & \left(\frac{1}{2} M R^{2}\right) \alpha=R f \tag{2}\ & \Rightarrow M a=2 f \end{align*} $$
त्यामुळे, $f=F / 3$. साटणारा नसल्यास,

$\Rightarrow f \leq \mu m g$
$\Rightarrow F \leq 3 \mu M g$.










