With the Calculus as a key, Mathematics can be successfully applied to the explanation of the course of Nature - WHITEHEAD

6.1 भूमिका (Introduction)

अध्याय 5 में हमने संयुक्त फलनों, प्रतिलोम त्रिकोणमितीय फलनों, अस्पष्ट फलनों, चरघातांकीय फलनों और लघुघातांकीय फलनों का अवकलज ज्ञात करना सीखा है। प्रस्तुत अध्याय में, हम गणित की विभिन्न शाखाओं में अवकलज के अनुप्रयोग का अध्ययन करेंगे यथा इंजिनियरिंग, विज्ञान, सामाजिक विज्ञान और कई दूसरे क्षेत्र। उदाहरण के लिए हम सीखेंगे कि किस प्रकार अवकलज का उपयोग (i) राशियों के परिवर्तन की दर ज्ञात करने में, (ii) किसी बिंदु पर स्पर्श रेखा तथा अभिलंब की समीकरण ज्ञात करने में, (iii) एक फलन के आलेख पर वर्तन बिंदु ज्ञात करने में, जो हमें उन बिंदुओं को ज्ञात करने में सहायक होता है जिन पर फलन का अधिकतम या न्यूनतम मान होता है। हम उन अंतरालों को ज्ञात करने में भी अवकलज का उपयोग करेंगे, जिनमें एक फलन वर्धमान या ह्रासमान होता है। अंततः हम कुछ राशियों के सन्निकट मान प्राप्त करने में अवकलज प्रयुक्त करेंगे।

6.2 राशियों के परिवर्तन की दर (Rate of Change of Quantities)

पुन: स्मरण कीजिए कि अवकलज $\frac{ds}{dt}$ से हमारा तात्पर्य समय अंतराल $t$ के सापेक्ष दूरी $s$ के परिवर्तन की दर से है। इसी प्रकार, यदि एक राशि $y$ एक दूसरी राशि $x$ के सापेक्ष किसी नियम $y=f(x)$ को संतुष्ट करते हुए परिवर्तित होती है तो $\frac{dy}{dx}($ या $f^{\prime }(x)),x$ के सापेक्ष $y$ के परिवर्तन की दर को प्रदर्शित करता है और ${\frac{dy}{dx}]}_{x=x_0}$ (या $f^{\prime }\left(x_0\right))x=x_0$ पर) $x$ के सापेक्ष $y$ की परिवर्तन की दर को प्रदर्शित करता है।

इसके अतिरिक्त, यदि दो राशियाँ $x$ और $y,t$ के सापेक्ष परिवर्तित हो रही हों अर्थात् $x=f(t)$ और $y=g(t)$ है तब शृंखला नियम से

$$\frac{dy}{dx}=\frac{dy}{dt}/\frac{dx}{dt},\text{ यदि }\frac{dx}{dt}\ne 0\text{ प्राप्त होता है। }$$

इस प्रकार, $x$ के सापेक्ष $y$ के परिवर्तन की दर का परिकलन $t$ के सापेक्ष $y$ और $x$ के परिवर्तन की दर का प्रयोग करके किया जा सकता है ।

आइए हम कुछ उदाहरणों पर विचार करें।

प्रश्नावली 6.1

1. वृत्त के क्षेत्रफल के परिवर्तन की दर इसकी त्रिज्या $r$ के सापेक्ष ज्ञात कीजिए जबकि

(a) $r=3\mathrm{cm}$ है।

(b) $r=4\mathrm{cm}$ है।

2. एक घन का आयतन $8{\mathrm{cm}}^3/\mathrm{s}$ की दर से बढ़ रहा है। पृष्ठ क्षेत्रफल किस दर से बढ़ रहा है जबकि इसके किनारे की लंबायीं $12\mathrm{cm}$ है।

3. एक वृत्त की त्रिज्या समान रूप से $3\mathrm{cm}/\mathrm{s}$ की दर से बढ़ रही है। ज्ञात कीजिए कि वृत्त का क्षेत्रफल किस दर से बढ़ रहा है जब त्रिज्या $10\mathrm{cm}$ है।

4. एक परिवर्तनशील घन का किनारा $3\mathrm{cm}/\mathrm{s}$ की दर से बढ़ रहा है। घन का आयतन किस दर से बढ़ रहा है जबकि किनारा $10\mathrm{cm}$ लंबा है?

5. एक स्थिर झील में एक पत्थर डाला जाता है ओर तरंगें वृत्तों में $5\mathrm{cm}/\mathrm{s}$ की गति से चलती हैं। जब वृत्ताकार तरंग की त्रिज्या $8\mathrm{cm}$ है तो उस क्षण, घिरा हुआ क्षेत्रफल किस दर से बढ़ रहा है?

6. एक वृत्त की त्रिज्या $0.7\mathrm{cm}/\mathrm{s}$ की दर से बढ़ रही है। इसकी परिधि की वृद्धि की दर क्या है जब $r=4.9\mathrm{cm}$ है?

7. एक आयत की लंबायीं $x,5\mathrm{cm}/\min$ की दर से घट रही है और चौड़ाई $y,4\mathrm{cm}/\min$ की दर से बढ़ रही है। जब $x=8\mathrm{cm}$ और $y=6\mathrm{cm}$ हैं तब आयत के (a) परिमाप (b) क्षेत्रफल के परिवर्तन की दर ज्ञात कीजिए।

8. एक गुब्बारा जो सदैव गोलाकार रहता है, एक पंप द्वारा $900{\mathrm{cm}}^3$ गैस प्रति सेकंड भर कर फुलाया जाता है। गुब्बारे की त्रिज्या के परिवर्तन की दर ज्ञात कीजिए जब त्रिज्या $15\mathrm{cm}$ है।

9. एक गुब्बारा जो सदैव गोलाकार रहता है, की त्रिज्या परिवर्तनशील है। त्रिज्या के सापेक्ष आयतन के परिवर्तन की दर ज्ञात कीजिए जब त्रिज्या $10\mathrm{cm}$ है।

10. एक $5\mathrm{m}$ लंबी सीढ़ी दीवार के सहारे झुकी है। सीढ़ी का नीचे का सिरा, जमीन के अनुदिश, दीवार से दूर $2\mathrm{cm}/\mathrm{s}$ की दर से खींचा जाता है। दीवार पर इसकी ऊँचाई किस दर से घट रही है जबकि सीढ़ी के नीचे का सिरा दीवार से $4\mathrm{m}$ दूर है?

11. एक कण वक्र $6y=x^3+2$ के अनुगत गति कर रहा हैं। वक्र पर उन बिंदुओं को ज्ञात कीजिए जबकि $x$-निर्देशांक की तुलना में $y$-निर्देशांक 8 गुना तीव्रता से बदल रहा है।

12. हवा के एक बुलबुले की त्रिज्या $\frac{1}{2}\mathrm{cm}/\mathrm{s}$ की दर से बढ़ रही है। बुलबुले का आयतन किस दर से बढ़ रहा है जबकि त्रिज्या $1\mathrm{cm}$ है?

13. एक गुब्बारा, जो सदैव गोलाकार रहता है, का परिवर्तनशील व्यास $\frac{3}{2}(2x+1)$ है। $x$ के सापेक्ष आयतन के परिवर्तन की दर ज्ञात कीजिए।

14. एक पाइप से रेत $12{\mathrm{cm}}^3/\mathrm{s}$ की दर से गिर रही है। गिरती रेत जमीन पर एक ऐसा शंकु बनाती है जिसकी ऊँचाई सदैव आधार की त्रिज्या का छठा भाग है। रेत से बने के शंकु की ऊँचाई किस दर से बढ़ रही है जबकि ऊँचाई $4\mathrm{cm}$ है?

15. एक वस्तु की $x$ इकाइयों के उत्पादन से संबंध कुल लागत $\mathrm{C}(x)$ (रुपये में)

$$C(x)=0.007x^3-0.003x^2+15x+4000$$

से प्रदत्त है। सीमांत लागत ज्ञात कीजिए जबकि 17 इकाइयों का उत्पादन किया गया है।

16. किसी उत्पाद की $x$ इकाइयों के विक्रय से प्राप्त कुल आय $\mathrm{R}(x)$ रुपयों में

$$R(x)=13x^2+26x+15$$

से प्रदत्त है। सीमांत आय ज्ञात कीजिए जब $x=7$ है।

प्रश्न 17 तथा 18 में सही उत्तर का चयन कीजिए:

17. एक वृत्त की त्रिज्या $r=6\mathrm{cm}$ पर $r$ के सापेक्ष क्षेत्रफल में परिवर्तन की दर है:

(A) $10\pi$

(B) $12\pi$

(C) $8\pi$

(D) $11\pi$

18. एक उत्पाद की $x$ इकाइयों के विक्रय से प्राप्त कुल आय रुपयों में $\mathrm{R}(x)=3x^2+36x+5$ से प्रदत्त है। जब $x=15$ है तो सीमांत आय है:

(A) 116

(B) 96

(C) 90

(D) 126

6.3 वर्धमान (Increasing) और ह्रासमान (Decreasing ) फलन

इस अनुच्छेद में हम अवकलन का प्रयोग करके यह ज्ञात करेंगे कि फलन वर्धमान है या ह्रासमान या इनमें से कोई नहीं है।

$f(x)=x^2,x\in \mathbf{R}$ द्वारा प्रदत्त फलन $f$ पर विचार कीजिए। इस फलन का आलेख आकृति 6.1 में दिया गया है।

मूल बिंदु के बायों ओर का मान

जैसे जैसे हम बाँए से दाँए ओर बढ़ते जाते हैं तो आलेख की ऊँचाई घटती जाती है। मूल बिंदु के दायीं ओर का मान

जैसे जैसे हम बाँए से दाँए ओर बढ़ते जाते है तो आलेख की ऊँचाई बढ़ती जाती है।

सर्वप्रथम मूल बिंदु के दायीं ओर के आलेख (आकृति 6.1) पर विचार करते हैं। यह देखिए कि आलेख के अनुदिश जैसे जैसे बाएँ से दाएँ ओर जाते हैं, आलेख की ऊँचाई लगातार बढ़ती जाती है। इसी कारण वास्तविक संख्याओं $x>0$ के लिए फलन वर्धमान कहलाता है।

अब मूल बिंदु के बायों ओर के आलेख पर विचार करते हैं। यहाँ हम देखते हैं कि जैसे जैसे आलेख के अनुदिश बाएँ से दाएँ की ओर जाते हैं, आलेख की ऊँचाई लगातार घटती जाती है। फलस्वरूप वास्तविक संख्याओं $x<0$ के लिए फलन ह्रासमान कहलाता है।

हम अब एक अंतराल में वर्धमान या ह्रासमान फलनों की निम्नलिखित विश्लेषणात्मक परिभाषा देंगे।

परिभाषा 1 मान लीजिए वास्तविक मान फलन $f$ के प्रांत में $\mathrm{I}$ एक अंतराल है। तब $f$

(i) अंतराल I में वर्धमान है, यदि I में $x_1<x_2\Rightarrow f\left(x_1\right)<f\left(x_2\right)$ सभी $x_1,x_2\in$ I के लिए

(ii) अंतराल I में ह्रासमान है, यदि I में $x_1<x_2\Rightarrow f\left(x_1\right)>f\left(x_2\right)$ सभी $x_1,x_2\in \mathrm{I}$ के लिए

(iii) अंतराल I में अचर है, यदि $f(x)=\mathrm{c},x\in \mathrm{I}$ जहाँ $\mathrm{c}$ एक अचर है।

इस प्रकार के फलनों का आलेखीय निरूपण आकृति 6.2 में देखिए।

वर्धमान फलन

(i)

अचर फलन

(ii)

निरंतर ह्रासमान फलन

(iii)

आकृति 6.2

अब हम एक बिंदु पर वर्धमान या ह्रासमान फलन को परिभाषित करेंगे।

परिभाषा 2 मान लीजिए कि वास्तविक मानों के परिभाषित फलन $f$ के प्रांत में एक बिंदु $x_0$ है तब $x_0$ पर $f$ वर्धमान और ह्रासमान कहलाता है यदि $x_0$ को अंतर्विष्ट करने वाले एक ऐसे विवृत्त अंतराल I का अस्तित्व इस प्रकार है कि I में, $f$ क्रमशः वर्धमान और ह्रासमान है आइए इस परिभाषा को वर्धमान फलन के लिए स्पष्ट करते हैं।

प्रमेय 1 मान लीजिए कि $f$ अंतराल $[a,b]$ पर संतत और विवृत्त अंतराल $(a,b)$ पर अवकलनीय है। तब

(a) $[a,b]$ में $f$ वर्धमान है यदि प्रत्येक $x\in (a,b)$ के लिए $f^{\prime }(x)>0$ है।

(b) $[a,b]$ में $f$ ह्रासमान है यदि प्रत्येक $x\in (a,b)$ के लिए $f^{\prime }(x)<0$ है।

(c) $[a,b]$ में $f$ एक अचर फलन है यदि प्रत्येक $x\in (a,b)$ के लिए $f^{\prime }(x)=0$ है।

उपपत्ति (a) मान लीजिए $x_1,x_2\in [a,b]$ इस प्रकार हैं कि $x_1<x_2$ तब मध्य मान प्रमेय से $x_1$ और $x_2$ के मध्य एक बिंदु $c$ का अस्तित्व इस प्रकार है कि

अर्थात्

$$f\left(x_2\right)-f\left(x_1\right)=f^{\prime }(c)(x_2-x_1)$$

अर्थात्

$$\begin{array}{ll}f\left(x_2\right)-f\left(x_1\right)>0& (\text{ क्योंकि }{f}^{\prime }(c)>0)\\ f\left(x_2\right)>f\left(x_1\right)& \end{array}$$

इस प्रकार, हम देखते हैं, कि

$$[a,b]\text{ के सभी }{x}_1,x_2\text{ के लिए }{x}_1<x_{2}f\left(x_1\right)f\left(x_2\right)$$

अतः $[a,b]$ में $f$ एक वर्धमान फलन है।

भाग (b) और (c) की उपपत्ति इसी प्रकार है। पाठकों के लिए इसे अभ्यास हेतु छोड़ा जाता है।

टिप्पणी

इस सदंर्भ में एक अन्य सामान्य प्रमेय के अनुसार यदि किसी अंतराल के अंत्य बिंदुओं के अतिरिक्त $f^{\prime }(x)>0$ जहाँ $x$, अंतराल में कोई अवयव है और $f$ उस अंतराल में संतत है तब $f$ को वर्धमान कहते हैं। इसी प्रकार यदि किसी अंतराल के अंत्य बिंदुओं के सिवाय $f^1(x)$ $<0$ जहाँ $x$ अंतराल का कोई अवयव है और $f$ उस अंतराल में संतत है तब $f$ को ह्रासमान कहते हैं।

प्रश्नावली 6.2

1. सिद्ध कीजिए $\mathbf{R}$ पर $f(x)=3x+17$ से प्रदत्त फलन वर्धमान है।

2. सिद्ध कीजिए कि $\mathbf{R}$ पर $f(x)=e^{2x}$ से प्रदत्त फलन वर्धमान है।

3. सिद्ध कीजिए $f(x)=\sin x$ से प्रदत्त फलन (a) $(0,\frac{\pi }{2})$ में वर्धमान है (b) $(\frac{\pi }{2},\pi )$ में ह्रासमान है (c) $(0,\pi )$ में न तो वर्धमान है और न ही ह्रासमान है।

4. अंतराल ज्ञात कीजिए जिनमें $f(x)=2x^2-3x$ से प्रदत्त फलन $f$ (a) वर्धमान (b) ह्रासमान

5. अंतराल ज्ञात कीजिए जिनमें $f(x)=2x^3-3x^2-36x+7$ से प्रदत्त फलन $f$ (a) वर्धमान (b) ह्रासमान

6. अंतराल ज्ञात कीजिए जिनमें निम्नलिखित फलन $f$ वर्धमान या ह्रासमान है:

(a) $f(x)x^2+2x+5$

(b) $f(x)10-6x-2x^2$

(c) $f(x)-2x^3-9x^2-12x+1$

(d) $f(x)6-9x-x^2$

(e) $f(x)(x+1{)}^3(x-3{)}^3$

7. सिद्ध कीजिए कि $y=\log (1+x)-\frac{2x}{2+x},x>-1$, अपने संपूर्ण प्रांत में एक वर्धमान फलन है।

8. $x$ के उन मानों को ज्ञात कीजिए जिनके लिए $y=[x(x-2){]}^2$ एक वर्धमान फलन है।

9. सिद्ध कीजिए कि $[0,\frac{\pi }{2}]$ में $y=\frac{4\sin \theta }{(2+\cos \theta )}-\theta ,\theta$ का एक वर्धमान फलन है।

10. सिद्ध कीजिए कि लघुगणकीय फलन $(0,\mathrm{\infty })$ में वर्धमान फलन है।

11. सिद्ध कीजिए कि $(-1,1)$ में $f(x)=x^2-x+1$ से प्रदत्त फलन न तो वर्धमान है और न ही ह्रासमान है।

12. निम्नलिखित में कौन से फलन $(0,\frac{\pi }{2})$ में ह्रासमान है ?

(A) $\cos x$

(B) $\cos 2x$

(C) $\cos 3x$

(D) $\tan x$

13. निम्नलिखित अंतरालों में से किस अंतराल में $f(x)=x^{100}+\sin x-1$ द्वारा प्रदत्त फलन $f$ ह्रासमान है?

(A) $(0,1)$

(B) $(\frac{\pi }{2},\pi )$

(C) $(0,\frac{\pi }{2})$

(D) इनमें से कोई नही

14. $a$ का वह न्यूनतम मान ज्ञात कीजिए जिसके लिए अंतराल $[1,2]$ में $f(x)=x^2+ax+1$ से प्रदत्त फलन वर्धमान है।

15. मान लीजिए $[-1,1]$ से असंयुक्त एक अंतराल $\mathrm{I}$ हो तो सिद्ध कीजिए कि $\mathrm{I}$ में $f(x)=x+\frac{1}{x}$ से प्रदत्त फलन $f$, वर्धमान है।

16. सिद्ध कीजिए कि फलन $f(x)=\log \sin x,(0,\frac{\pi }{2})$ में वर्धमान और $(\frac{\pi }{2},\pi )$ में ह्रासमान है।

17. सिद्ध कीजिए कि फलन $f(x)=\log |\cos x|(0,\frac{\pi }{2})$ में वर्धमान और $(\frac{3\pi }{2},2\pi )$ में ह्रासमान है।

18. सिद्ध कीजिए कि $\mathbf{R}$ में दिया गया फलन $f(x)=x^3-3x^2+3x-100$ वर्धमान है।

19. निम्नलिखित में से किस अंतराल में $y=x^2{e}^{-x}$ वर्धमान है?

(A) $(-\mathrm{\infty },\mathrm{\infty })$

(B) $(-2,0)$

(C) $(2,\mathrm{\infty })$

(D) $(0,2)$

6.4 उच्चतम और निम्नतम (Maxima and Minima)

इस अनुच्छेद में, हम विभिन्न फलनों के उच्चतम और निम्नतम मानों की गणना करने में अवकलज की संकल्पना का प्रयोग करेंगे। वास्तव में हम एक फलन के आलेख के वर्तन बिंदुओं (Turning points) को ज्ञात करेंगे और इस प्रकार उन बिंदुओं को ज्ञात करेंगे जिन पर आलेख स्थानीय अधिकतम (या न्यूनतम) पर पहुँचता है। इस प्रकार के बिंदुओं का ज्ञान एक फलन का आलेख खींचने में बहुत उपयोगी होता है। इसके अतिरिक्त हम एक फलन का निरपेक्ष उच्चतम मान (Absolute maximum value) ओर निरपेक्ष न्यूनतम मान (Absolute minimum value) भी ज्ञात करेंगे जो कई अनुप्रयुक्त समस्याओं के हल के लिए आवश्यक हैं।

आइए हम दैनिक जीवन की निम्नलिखित समस्याओं पर विचार करें

(i) संतरों के वृक्षों के एक बाग से होने वाला लाभ फलन $\mathrm{P}(x)=ax+b{x}^2$ द्वारा प्रदत्त है जहाँ $a,b$ अचर हैं और $x$ प्रति एकड़ में संतरे के वृक्षों की संख्या है। प्रति एकड़ कितने वृक्ष अधिकतम लाभ देगें?

(ii) एक $60\mathrm{m}$ ऊँचे भवन से हवा में फेंकी गई एक गेंद $h(x)=60+x-\frac{x^2}{60}$ के द्वारा निर्धारित पथ के अनुदिश चलती है, जहाँ $x$ भवन से गेंद की क्षैतिज दूरी और $h(x)$ उसकी ऊँचाई है। गेंद कितनी अधिकतम ऊँचाई तक पहुँचेगी?

(iii) शत्रु का एक अपाचे हेलिकॉप्टर वक्र $f(x)=x^2+7$ द्वारा प्रदत्त पथ के अनुदिश उड़ रहा है। बिंदु $(1,2)$ पर स्थित एक सैनिक उस हेलिकॉप्टर को गोली मारना चाहता है जब हेलिकॉप्टर उसके निकटतम हो। यह निकटतम दूरी कितनी है?

उपर्युक्त समस्याओं में कुछ सर्वसामान्य है अर्थात् हम प्रदत्त फलनों के उच्चतम अथवा निम्नतम मान ज्ञात करना चाहते हैं। इन समस्याओं को सुलझाने के लिए हम विधिवत एक फलन का अधिकतम मान या न्यूनतम मान व स्थानीय उच्चतम व स्थानीय निम्नतम के बिंदुओं और इन बिंदुओं को निर्धारित करने के परीक्षण को परिभाषित करेंगे।

परिभाषा 3 मान लीजिए एक अंतराल I में एक फलन $f$ परिभाषित है, तब

(a) $f$ का उच्चतम मान $\mathrm{I}$ में होता है, यदि $\mathrm{I}$ में एक बिंदु $c$ का अस्तित्व इस प्रकार है कि $f(c)\ge f(x),\mathrm{\forall }x\in \mathrm{I}$

संख्या $f(c)$ को $\mathrm{I}$ में $f$ का उच्चतम मान कहते हैं और बिंदु $c$ को $\mathrm{I}$ में $f$ के उच्चतम मान वाला बिंदु कहा जाता है।

(b) $f$ का निम्नतम मान $\mathrm{I}$ में होता है यदि $\mathrm{I}$ में एक बिंदु $c$ का अस्तित्व है इस प्रकार कि $f(c)\le f(x),\mathrm{\forall }x\in \mathrm{I}$

संख्या $f(c)$ को $\mathrm{I}$ में $f$ का निम्नतम मान कहते हैं और बिंदु $c$ को $\mathrm{I}$ में $f$ के निम्नतम मान वाला बिंदु कहा जाता है।

(c) I में $f$ एक चरम मान (extreme value) रखने वाला फलन कहलाता है यदि $\mathrm{I}$ में एक ऐसे बिंदु $c$ का अस्तित्व इस प्रकार है कि $f(c),f$ का उच्चतम मान अथवा निम्नतम मान है।

इस स्थिति में $f(c),\mathrm{I}$ में $f$ का चरम मान कहलाता है और बिंदु $c$ एक चरम बिंदु कहलाता है।

(a)

(b)

(c)

आकृति 6.7

टिप्पणी आकृति 6.7 (a), (b) और (c) में हमने कुछ विशिष्ट फलनों के आलेख प्रदर्शित किए हैं जिनसे हमें एक बिंदु पर उच्चतम मान और निम्नतम मान ज्ञात करने में सहायता मिलती है। वास्तव में आलेखों से हम उन फलनों के जो अवकलित नहीं होते हैं। उच्चतम / निम्नतम मान भी ज्ञात कर सकते हैं, (उदाहरण 27)।

टिप्पणी यदि हम फलन के प्रांत को केवल $[-2,1]$ तक सीमित करें तब $x=-2$ पर $f$ का उच्चतम मान $(-2{)}^2=4$ है।

टिप्पणी

(i) यदि हम फलन के प्रांत को केवल $[-2,1]$ तक सीमित करें, तो $f$ का उच्चतम मान $|-2|=2$ होगा।

(ii) उदाहरण 27 में ध्यान दें कि फलन $f,x=0$ पर अवकलनीय नहीं है।

टिप्पणी पाठक देख सकते हैं कि उदाहरण 28 में यदि $f$ के प्रांत में 0 और 1 को सम्मिलित कर लिया जाए अर्थात $f$ के प्रांत को बढ़ाकर $[0,1]$ कर दिया जाए तो फलन का निम्नतम मान $x=0$ पर 0 और उच्चतम मान $x=1$ पर 1 है। वास्तव में हम निम्नलिखित परिणाम पाते हैं (इन परिणामों की उपपत्ति इस पुस्तक के क्षेत्र से बाहर है)।

प्रत्येक एकदिष्ट (monotonic) फलन अपने परिभाषित प्रांत के अंत्य बिंदुओं पर उच्चतम/निम्नतम ग्रहण करता है।

इस परिणाम का अधिक व्यापक रूप यह है कि संवृत्त अंतराल पर प्रत्येक संतत फलन के उच्चतम और निम्नष्ठ मान होते हैं।

टिप्पणी किसी अंतराल I में एकदिष्ट फलन से हमारा अभिप्राय है कि I में फलन या तो वर्धमान है या ह्रासमान है।

इस अनुच्छेद में एक संवृत्त अंतराल पर परिभाषित फलन के उच्चतम और निम्नतम मानों के बारे में बाद में विचार करेंगे।

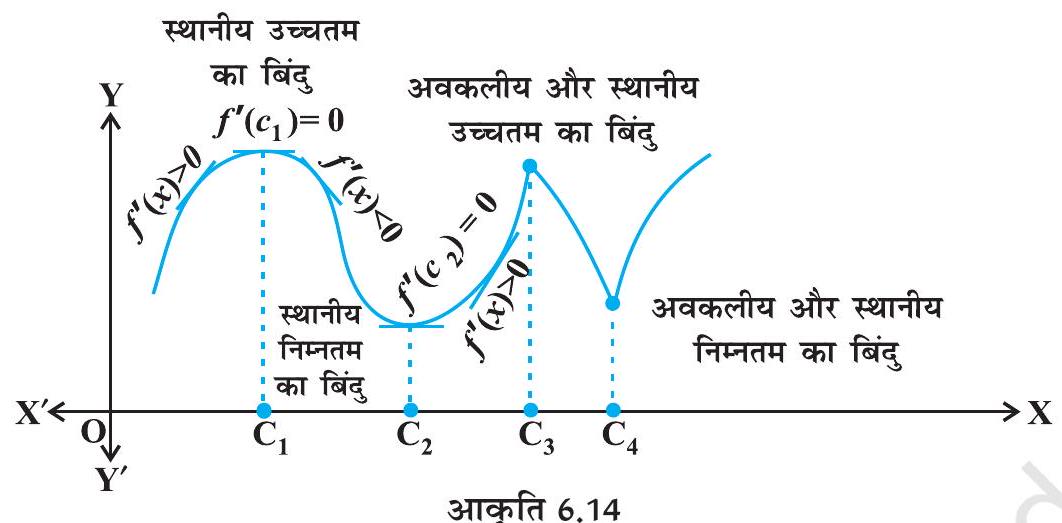
आइए अब आकृति 6.11 में दर्शाए गए किसी फलन के आलेख का अध्ययन करें। देखिए कि फलन का आलेख बिंदुओं $\mathrm{A},\mathrm{B},\mathrm{C}$ तथा $\mathrm{D}$ पर वर्धमान से ह्रासमान या विलोमतः ह्रासमान से वर्धमान होता है। इन बिंदुओं को फलन के वर्तन बिंदु कहते हैं। पुनः ध्यान दीजिए कि वर्तन बिंदुओं पर आलेख में एक छोटी पहाड़ी या छोटी घाटी बनती है। मोटे तौर पर बिंदुओं $\mathrm{A}$ तथा $\mathrm{C}$ में से प्रत्येक के सामीप्य (Neighbourhood) में फलन का निम्नतम मान है, जो उनकी अपनी-अपनी घाटियों के अधोभागों (Bottom) पर है। इसी प्रकार बिंदुओं $\mathrm{B}$ तथा $\mathrm{D}$ में से प्रत्येक के सामीप्य में फलन का उच्चतम मान है, जो उनकी अपनी-अपनी पहाड़ियों के शीर्षों पर है। इस कारण से बिंदुओं $\mathrm{A}$ तथा $\mathrm{C}$ को स्थानीय

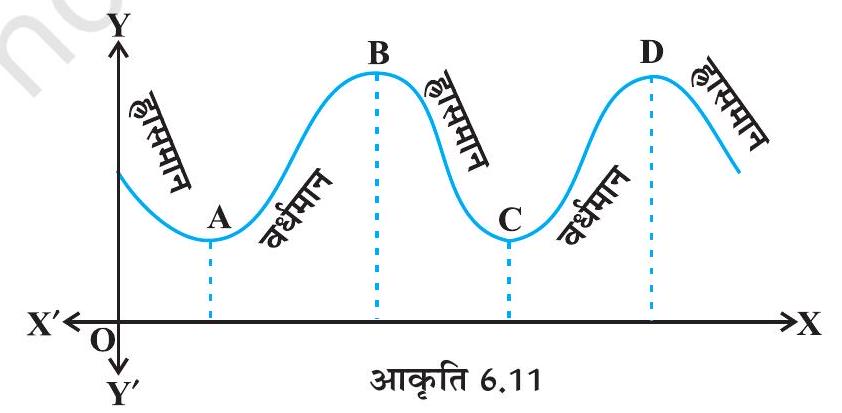
निम्नतम मान (या सापेक्ष निम्नतम मान) का बिंदु तथा $\mathrm{B}$ और $\mathrm{D}$ को स्थानीय उच्चतम मान (या सापेक्ष उच्चतम मान) के बिंदु समझा जा सकता है। फलन के स्थानीय उच्चतम मान और स्थानीय निम्नतम मानों को क्रमशः फलन का स्थानीय उच्चतम और स्थानीय निम्नतम कहा जाता है।

अब हम औपचारिक रूप से निम्नलिखित परिभाषा देते हैं।

परिभाषा 4 मान लीजिए $f$ एक वास्तविक मानीय फलन है और $c$ फलन $f$ के प्रांत में एक आंतरिक बिंदु है। तब

(a) $c$ को स्थानीय उच्चतम का बिंदु कहा जाता है यदि एक ऐसा $h>0$ है कि $(c-h,c+h)$ में सभी $x$ के लिए $f(c)\ge f(x)$ हो। तब $f(c)$, फलन $f$ का स्थानीय उच्चतम मान कहलाता है।

(b) $c$ को स्थानीय निम्नतम का बिंदु कहा जाता है यदि एक ऐसा $h>0$ है कि $(c-h,c+h)$ में सभी $x$ के लिए $f(c)<f(x)$ हो। तब $f(c)$, फलन $f$ का स्थानीय निम्नतम मान कहलाता है।

ज्यामितीय दृष्टिकोण से, उपर्युक्त परिभाषा का अर्थ है कि यदि $x=c$, फलन $f$ का स्थानीय उच्चतम का बिंदु है, तो $c$ के आसपास का आलेख आकृति 6.12(a) के अनुसार होगा। ध्यान दीजिए कि अंतराल $(c-h,c)$ में फलन $f$ वर्धमान (अर्थात् $f^{\prime }(x)>0$ ) और अंतराल $(c,c+h)$ में फलन ह्रासमान (अर्थात् $f^{\prime }(x)<0$ ) है।

इससे यह निष्कर्ष निकलता है कि $f^{\prime }(c)$ अवश्य ही शून्य होना चाहिए।

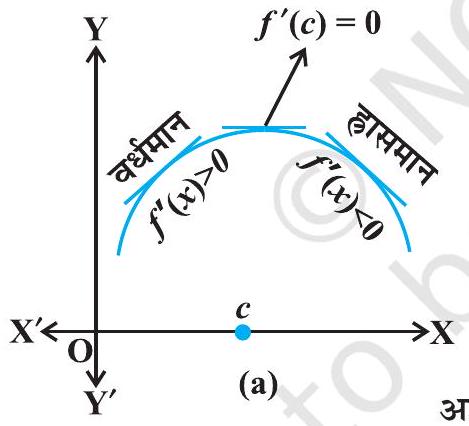
आकृति 6.12

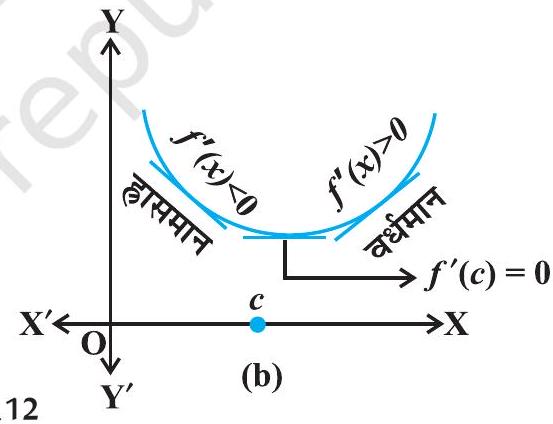
इसी प्रकार, यदि $c$, फलन $f$ का स्थानीय निम्नतम बिंदु है तो $c$ के आसपास का आलेख आकृति 6.14(b) के अनुसार होगा। यहाँ अंतराल $(c-h,c)$ में $f$ ह्रासमान (अर्थात् $f^{\prime }(x)<0)$ है और अंतराल $(c,c+h)$ में $f$ वर्धमान (अर्थात, $f^{\prime }(x)>0$ ) है। यह पुनः सुझाव देता है कि $f^{\prime }(c)$ अवश्य ही शून्य होना चाहिए।

उपर्युक्त परिचर्चा से हमें निम्नलिखित परिभाषा प्राप्त होती है (बिना उपपत्ति)।

प्रमेय 2 मान लीजिए एक विवृत्त अंतराल $\mathrm{I}$ में $f$ एक परिभाषित फलन है। मान लीजिए $c\in \mathrm{I}$ कोई बिंदु है। यदि $f$ का $x=c$ पर एक स्थानीय उच्चतम या एक स्थानीय निम्नतम का बिंदु है तो $f^{\prime }(c)$ $=0$ है या $f$ बिंदु $c$ पर अवकलनीय नहीं है।

टिप्पणी उपरोक्त प्रमेय का विलोम आवश्यक नहीं है कि सत्य हो जैसे कि एक बिंदु जिस पर अवकलज शून्य हो जाता है तो यह आवश्यक नहीं है कि वह स्थानीय उच्चतम या स्थानीय निम्नतम का बिंदु है। उदाहरणतया यदि $f(x)=x^3$ हो तो $f^{\prime }(x)=3x^2$ और इसलिए $f^{\prime }(0)=0$ है। परन्तु 0 न तो स्थानीय उच्चतम और न ही स्थानीय निम्नतम बिंदु है। आकृति 6.15

टिप्पणी फलन $f$ के प्रांत में एक बिंदु $c$, जिस पर या तो $f^{\prime }(c)=0$ है या $f$ अवकलनीय नहीं है, $f$ का क्रांतिक बिंदु (Critical Point) कहलाता है। ध्यान दीजिए कि यदि $f$ बिंदु $c$ पर संतत है और $f^{\prime }(c)=0$ है तो यहाँ एक ऐसे $h>0$ का अस्तित्व है कि अंतराल $(c-h,c+h)$ में $f$ अवकलनीय है।

अब हम केवल प्रथम अवकलजों का प्रयोग करके स्थानीय उच्चतम बिंदु या स्थानीय निम्नतम बिंदुओं को ज्ञात करने की क्रियाविधि प्रस्तुत करेंगे।

प्रमेय 3 (प्रथम अवकलज परीक्षण) मान लीजिए कि एक फलन $f$ किसी विवृत्त अंतराल I पर परिभाषित है। मान लीजिए कि $f$ अंतराल $\mathrm{I}$ में स्थित क्रांतिक बिंदु $c$ पर संतत है। तब

(i) $x$ के बिंदु $c$ से हो कर बढ़ने के साथ-साथ, यदि $f^{\prime }(x)$ का चिह्न धन से ऋण में परिवर्तित होता है अर्थात् यदि बिंदु $c$ के बायों ओर और उसके पर्याप्त निकट के प्रत्येक बिंदु पर $f^{\prime }(x)>0$ तथा $c$ के दायीं ओर और पर्याप्त निकट के प्रत्येक बिंदु पर $f^{\prime }(x)<0$ हो तो $c$ स्थानीय उच्चतम एक बिंदु है।

(ii) $x$ के बिंदु $c$ से हो कर बढ़ने के साथ-साथ यदि $f^{\prime }(x)$ का चिह्न ऋण से धन में परिवर्तित होता है, अर्थात् यदि बिंदु $c$ के बायों ओर और उसके पर्याप्त निकट के प्रत्येक बिंदु पर $f^{\prime }(x)<0$ तथा $c$ के दायीं ओर और उसके पर्याप्त निकट के प्रत्येक बिंदु पर $f^{\prime }(x)>0$ हो तो $c$ स्थानीय निम्नतम बिंदु है।

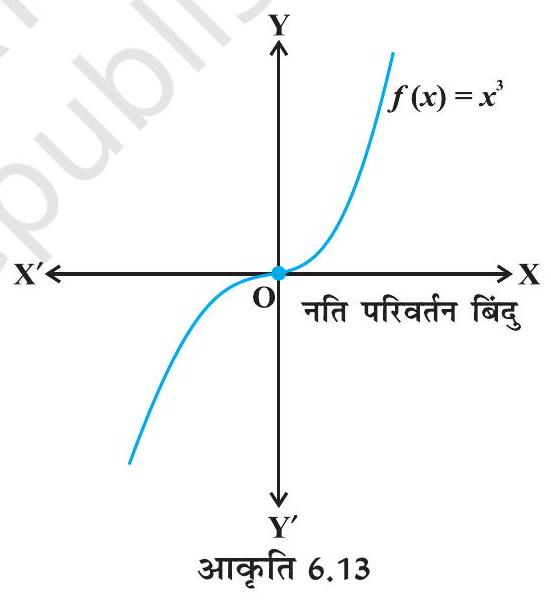
(iii) $x$ के बिंदु $c$ से हो कर बढ़ने के साथ यदि $f^{\prime }(x)$ का चिह्न परिवर्तित नहीं होता है, तो $c$ न तो स्थानीय उच्चतम बिंदु है और न स्थानीय निम्नतम बिंदु। वास्तव में, इस प्रकार के बिंदु को नति परिवर्तन बिंदु (Point of Inflection) (आकृति 6.13) कहते हैं।

5 टिप्पणी यदि $c$ फलन $f$ का एक स्थानीय उच्चतम बिंदु है तो $f(c)$ फलन $f$ का स्थानीय उच्चतम मान है। इसी प्रकार, यदि $c$ फलन $f$ का एक स्थानीय निम्नतम बिंदु है, तो $f(c)$ फलन $f$ का स्थानीय निम्नतम मान है। आकृतियाँ 6.13 और 6.14 प्रमेय 3 की ज्यामितीय व्याख्या करती है।

टिप्पणी ध्यान दीजिए कि उदाहरण 30 में $f^{\prime }(x)$ का चिह्न अंतराल $\mathbf{R}$ में कभी भी नहीं बदलता। अतः $f$ के आलेख में कोई भी वर्तन बिंदु नहीं है और इसलिए स्थानीय उच्चतम या स्थानीय निम्नतम का कोई भी बिंदु नहीं है।

अब हम किसी प्रदत्त फलन के स्थानीय उच्चतम और स्थानीय निम्नतम के परीक्षण के लिए एक दूसरी क्रियाविधि प्रस्तुत करेंगे। यह परीक्षण प्रथम अवकलज परीक्षण की तुलना में प्रायः सरल है। प्रमेय 4 मान लीजिए कि $f$, किसी अंतराल $\mathrm{I}$ में परिभाषित एक फलन है तथा $c\in \mathrm{I}$ है। मान लीजिए कि $f,c$ पर दो बार लगातार अवकलनीय है। तब

(i) यदि $f^{\prime }(c)=0$ और $f^{\prime \prime }(c)<0$ तो $x=c$ स्थानीय उच्चतम का एक बिंदु है। इस दशा में $f$ का स्थानीय उच्चतम मान $f(c)$ है।

(ii) यदि $f^{\prime }(c)=0$ और $f^{\prime \prime }(c)>0$ तो $x=c$ स्थानीय निम्नतम का एक बिंदु है। इस दशा में $f$ का स्थानीय निम्नतम मान $f(c)$ है।

(iii) यदि $f^{\prime }(c)=0$ और $f^{\prime \prime }(c)=0$ है तो यह परीक्षण असफल हो जाता है। इस स्थिति में हम पुनः प्रथम अवकलज परीक्षण पर वापस जाकर यह ज्ञात करते हैं कि $c$ उच्चतम, निम्नतम या नति परिवर्तन का बिंदु है।

टिप्पणी बिंदु $c$ पर $f$ दो बार लगातार अवकलनीय है इससे हमारा तात्पर्य कि $c$ पर $f$ के द्वितीय अवकलज का अस्तित्व है।

6.4.1 एक संवृत्त अंतराल में किसी फलन का उच्चतम और निम्नतम मान (Maximum and Minimum Values of a Function in a Closed Interval)

मान लीजिए $f(x)=x+2,x\in (0,1)$ द्वारा प्रदत्त एक प्रलन $f$ है।

ध्यान दीजिए कि $(0,1)$ पर फलन संतत है और इस अंतराल में न तो इसका कोई उच्चतम मान है और न ही इसका कोई निम्नतम मान है।

तथापि, यदि हम $f$ के प्रांत को संवृत्त अंतराल $[0,1]$ तक बढ़ा दें तब भी $f$ का शायद कोई स्थानीय उच्चतम (निम्नतम) मान नहीं होगा परंतु इसका निश्चित ही उच्चतम मान $3=f(1)$ और

निम्नतम मान $2=f(0)$ हैं। $x=1$ पर $f$ का उच्चतम मान $3,[0,1]$ पर $f$ का निरपेक्ष उच्चतम मान (महत्तम मान) (absolute maximum value) या सार्वत्रिक अधिकतम मान (global maximum or greatest value) कहलाता है। इसी प्रकार, $x=0$ पर $f$ का निम्नतम मान $2,[0,1]$ पर $f$ का निरपेक्ष निम्नतम मान (न्यूनतम मान) (absolute minimum value) या सार्वत्रिक न्यूनतम मान (global minimum or least value) कहलाता है।

एक संवृत्त अंतराल $[a,b]$ पर परिभाषित किसी संतत फलन $f$ के संगत आकृति 6.19 में प्रदर्शित आलेख पर विचार कीजिए कि $x=b$ पर फलन $f$ का स्थानीय निम्नतम है तथा स्थानीय निम्नतम मान $f(b)$ है। फलन का $x=c$ पर स्थानीय उच्चतम बिंदु है तथा स्थानीय उच्चतम मान $f(c)$ है।

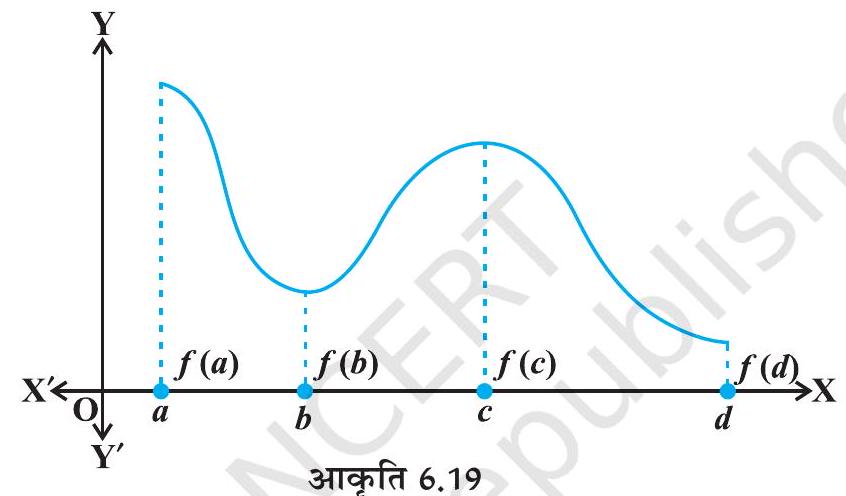
साथ ही आलेख से यह भी स्पष्ट है कि $f$ का निरपेक्ष उच्चतम मान $f(a)$ तथा निरपेक्ष निम्नतम मान $f(d)$ है। इसके अतिरिक्त ध्यान दीजिए कि $f$ का निरपेक्ष उच्चतम (निम्नतम) मान स्थानीय उच्चतम (निम्नतम) मान से भिन्न है।

अब हम एक संवृत्त अंतराल I में एक फलन के निरपेक्ष उच्चतम और निरपेक्ष निम्नतम के विषय में दो परिणामों (बिना उपपत्ति) के कथन बताएँगे।

प्रमेय 5 मान लीजिए एक अंतराल $\mathrm{I}=[a,b]$ पर $f$ एक संतत फलन है। तब $f$ का निरपेक्ष उच्चतम मान होता है और $\mathrm{I}$ में कम से कम एक बार $f$ यह मान प्राप्त करता है तथा $f$ का निरपेक्ष निम्नतम मान होता है और $\mathrm{I}$ में कम से कम एक बार $f$ यह मान प्राप्त करता है।

प्रमेय 6 मान लीजिए संवृत्त अंतराल $\mathrm{I}$ पर $f$ एक अवकलनीय फलन है और मान लीजिए कि I का कोई आंतरिक बिंदु $c$ है। तब

(i) यदि $c$ पर $f$ निरपेक्ष उच्चतम मान प्राप्त करता है, तो $f^{\prime }(c)=0$

(ii) यदि $c$ पर $f$ निरपेक्ष निम्नतम मान प्राप्त करता है, तो $f^{\prime }(c)=0$

उपर्युक्त प्रमेयों के विचार से, दिए गए संवृत्त अंतराल में किसी फलन के निरपेक्ष उच्चतम मान और निरपेक्ष निम्नतम मान ज्ञात करने के लिए विधि निम्नलिखित हैं।

व्यावहारिक विधि (Working Rule)

चरण 1: दिए गए अंतराल में $f$ के सभी क्रांतिक बिंदु ज्ञात कीजिए अर्थात् $x$ के वह सभी मान ज्ञात कीजिए जहाँ या तो $f^{\prime }(x)=0$ या $f$ अवकलनीय नहीं है।

चरण 2: अंतराल के अंत्य बिंदु लीजिए।

चरण 3: इन सभी बिंदुओं पर (चरण 1 व 2 में सूचीबद्ध) $f$ के मानों की गणना कीजिए।

चरण 4: चरण 3 में गणना से प्राप्त $f$ के मानों में से उच्चतम और निम्नतम मानों को लीजिए। यही उच्चतम मान, $f$ का निरपेक्ष उच्चतम मान और निम्नतम मान, $f$ का निरपेक्ष निम्नतम मान होंगे।

प्रश्नावली 6.3

1. निम्नलिखित दिए गए फलनों के उच्चतम या निम्नतम मान, यदि कोई तो, ज्ञात कीजिए:

(i) $f(x)=(2x-1{)}^2+3$

(ii) $f(x)=9x^2+12x+2$

(iii) $f(x)=-(x-1{)}^2+10$

(iv) $g(x)=x^3+1$

2. निम्नलिखित दिए गए फलनों के उच्चतम या निम्नतम मान, यदि कोई हों, तो ज्ञात कीजिए:

(i) $f(x)=|x+2|-1$

(ii) $g(x)=-|x+1|+3$

(iii) $h(x)=\sin (2x)+5$

(iv) $f(x)=|\sin 4x+3|$

(v) $h(x)=x+1,x\in (-1,1)$

3. निम्नलिखित फलनों के स्थानीय उच्चतम या निम्नतम, यदि कोई हों तो, ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम मान, जैसी स्थिति हो, भी ज्ञात कीजिए।

(i) $f(x)=x^2$

(ii) $g(x)=x^3-3x$

(iii) $h(x)=\sin x+\cos x,0<x<\frac{\pi }{2}$

(iv) $f(x)=\sin x-\cos x,0<x<2\pi$

$\begin{array}{ll}\text{ (v) }f(x)=x^3-6x^2+9x+15& \text{ (vi) }g(x)=\frac{x}{2}+\frac{2}{x},x>0\end{array}$

(vii) $g(x)=\frac{1}{x^2+2}$ (viii) $f(x)=x\sqrt{1-x},0<x<1$

4. सिद्ध कीजिए कि निम्नलिखित फलनों का उच्चतम या निम्नतम मान नहीं है:

(i) $f(x)=e^x$

(ii) $g(x)=\log x$

(iii) $h(x)=x^3+x^2+x+1$

5. प्रदत्त अंतरालों में निम्नलिखित फलनों के निरपेक्ष उच्चतम मान और निरपेक्ष निम्नतम मान ज्ञात कीजिए।

(i) $f(x)=x^3,x\in [-2,2]$

(ii) $f(x)=\sin x+\cos x,x\in [0,\pi ]$

(iii) $f(x)=4x-\frac{1}{2}{x}^2,x\in [-2,\frac{9}{2}]$ (iv) $f(x)=(x-1{)}^2+3,x\in [-3,1]$

6. यदि लाभ फलन $p(x)=41-72x-18x^2$ से प्रदत्त है तो किसी कंपनी द्वारा अर्जित उच्चतम लाभ ज्ञात कीजिए।

7. अंतराल $[0,3]$ पर $3x^4-8x^3+12x^2-48x+25$ के उच्चतम मान ओर निम्नतम मान ज्ञात कीजिए।

8. अंतराल $[0,2\pi ]$ के किन बिंदुओं पर फलन $\sin 2x$ अपना उच्चतम मान प्राप्त करता है?

9. फलन $\sin x+\cos x$ का उच्चतम मान क्या है?

10. अंतराल $[1,3]$ में $2x^3-24x+107$ का महत्तम मान ज्ञात कीजिए। इसी फलन का अंतराल $[-3,-1]$ में भी महत्तम मान ज्ञात कीजिए।

11. यदि दिया है कि अंतराल $[0,2]$ में $x=1$ पर फलन $x^4-62x^2+ax+9$ उच्चतम मान प्राप्त करता है, तो $a$ का मान ज्ञात कीजिए।

12. $[0,2\pi ]$ पर $x+\sin 2x$ का उच्चतम और निम्नतम मान ज्ञात कीजिए।

13. ऐसी दो संख्याएँ ज्ञात कीजिए जिनका योग 24 है और जिनका गुणनफल उच्चतम हो।

14. ऐसी दो धन संख्याएँ $x$ और $y$ ज्ञात कीजिए ताकि $x+y=60$ और $x{y}^3$ उच्चतम हो।

15. ऐसी दो धन संख्याएँ $x$ और $y$ ज्ञात कीजिए जिनका योग 35 हो और गुणनफल $x^2{y}^5$ उच्चतम हो।

16. ऐसी दो धन संख्याएँ ज्ञात कीजिए जिनका योग 16 हो और जिनके घनों का योग निम्नतम हो।

17. $18\mathrm{cm}$ भुजा के टिन के किसी वर्गाकार टुकड़े से प्रत्येक कोने पर एक वर्ग काटकर तथा इस प्रकार बनें टिन के फलकों को मोड़ कर ढक्कन रहित एक संदूक बनाना है। काटे जाने वाले वर्ग की भुजा कितनी होगी जिससे संदूक का आयतन उच्चतम हो?

18. $45\mathrm{cm}\times 24\mathrm{cm}$ की टिन की आयताकार चादर के कोनों पर वर्ग काटकर तथा इस प्रकार बनें टिन के फलकों को मोड़कर ढक्कन रहित एक संदूक बनाना है। काटे जाने वाले वर्ग की भुजा कितनी होगी जिससे संदूक का आयतन उच्चतम हो।

19. सिद्ध किजिए कि एक दिए वृत्त के अंतर्गत सभी आयतों में वर्ग का क्षेत्रफल उच्चतम होता है।

20. सिद्ध किजिए कि प्रदत्त पृष्ठ एवं महत्तम आयतन के बेलन की ऊँचाई, आधार के व्यास के बराबर होती है।

21. $100{\mathrm{cm}}^3$ आयतन वाले डिब्बे सभी बंद बेलनाकार (लंब वृत्तीय) डिब्बों में से न्यूनतम पृष्ठ क्षेत्रफल वाले डिब्बे की विमाएँ ज्ञात किजिए।

22. एक $28\mathrm{cm}$ लंबे तार को दो टुकड़ों में विभक्त किया जाना है। एक टुकड़े से वर्ग तथा दूसरे वे वृत्त बनाया जाना है। दोनों टुकड़ों की लंबायीं कितनी होनी चाहिए जिससे वर्ग एवं वृत्त का सम्मिलित क्षेत्रफल न्यूनतम हो?

23. सिद्ध कीजिए कि $R$ त्रिज्या के गोले के अंतर्गत विशालतम शंकु का आयतन, गोले के आयतन का $\frac{8}{27}$ होता है।

24. सिद्ध कीजिए कि न्यूनतम पृष्ठ का दिए आयतन के लंब वृत्तीय शंकु की ऊँचाई, आधार की त्रिज्या की $\sqrt{2}$ गुनी होती है।

25. सिद्ध कीजिए कि दी हुई तिर्यक ऊँचाई और महत्तम आयतन वाले शंकु का अर्ध शीर्ष कोण ${\tan }^{-1}\sqrt{2}$ होता है।

26. सिद्ध कीजिए कि दिए हुए पृष्ठ और महत्तम आयतन वाले लंब वृत्तीय शंकु का अर्ध शीर्ष कोण ${\sin }^{-1}\left(\frac{1}{3}\right)$ होता है।

प्रश्न संख्या 27 से 29 में सही उत्तर का चुनाव कीजिए।

27. वक्र $x^2=2y$ पर $(0,5)$ से न्यूनतम दूरी पर स्थित बिंदु है: (A) $(2\sqrt{2},4)$ (B) $(2\sqrt{2},0)$ (C) $(0,0)$ (D) $(2,2)$

28. $x$, के सभी वास्तविक मानों के लिए $\frac{1-x+x^2}{1+x+x^2}$ का न्यूनतम मान है: (A) 0 (B) 1 (C) 3 (D) $\frac{1}{3}$

29. $[x(x-1)+1{]}^{\frac{1}{3}},0\le x\le 1$ का उच्चतम मान है: (A) ${\left(\frac{1}{3}\right)}^{\frac{1}{3}}$ (B) $\frac{1}{2}$ (C) 1 (D) 0

अध्याय 6 पर विविध प्रश्नावली

1. सिद्ध कीजिए कि $f(x)=\frac{\log x}{x}$ द्वारा प्रदत्त फलन $x=e$ पर उच्चतम है।

2. किसी निश्चित आधार $b$ के एक समद्विबाहु त्रिभुज की समान भुजाएँ $3\mathrm{cm}/\mathrm{s}$ की दर से घट रहीं है। उस समय जब त्रिभुज की समान भुजाएँ आधार के बराबर हैं, उसका क्षेत्रफल कितनी तेजी से घट रहा है।

3. अंतराल ज्ञात कीजिए जिन पर

$$f(x)=\frac{4\sin x-2x-x\cos x}{2+\cos x}$$

से प्रदत्त फलन $f$ (i) निरंतर वर्धमान (ii) निरंतर ह्रासमान है।

4. अंतराल ज्ञात कीजिए जिन पर $f(x)=x^3+\frac{1}{x^3},x\ne 0$ से प्रदत्त फलन

(i) वर्धमान (ii) ह्रासमान है।

5. दीर्घवृत्त $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ के अंतर्गत उस समद्विबाहु त्रिभुज का महत्तम क्षेत्रफल ज्ञात कीजिए जिसका शीर्ष दीर्घ अक्ष का एक सिरा है।

6. आयताकार आधार व आयताकार दीवारों की $2\mathrm{m}$ गहरी और $8{\mathrm{m}}^3$ आयतन की एक बिना ढक्कन की टंकी का निर्माण करना है। यदि टंकी के निर्माण में आधार के लिए Rs $70/{\mathrm{m}}^2$ और दीवारों पर $\mathrm{Rs}45/{\mathrm{m}}^2$ व्यय आता है तो निम्नतम खर्च से बनी टंकी की लागत क्या है?

7. एक वृत्त और एक वर्ग के परिमापों का योग $k$ है, जहाँ $k$ एक अचर है। सिद्ध कीजिए कि उनके क्षेत्रफलों का योग निम्नतम है, जब वर्ग की भुजा वृत्त की त्रिज्या की दुगुनी है।

8. किसी आयत के ऊपर बने अर्धवृत्त के आकार वाली खिड़की है। खिड़की का संपूर्ण परिमाप $10\mathrm{m}$ है। पूर्णतया खुली खिड़की से अधिकतम प्रकाश आने के लिए खिड़की की विमाएँ ज्ञात कीजिए।

9. त्रिभुज की भुजाओं से $a$ और $b$ दूरी पर त्रिभुज के कर्ण पर स्थित एक बिंदु है। सिद्ध कीजिए कि कर्ण की न्यूनतम लंबाई ${(a^{\frac{2}{3}}+b^{\frac{2}{3}})}^{\frac{3}{2}}$ है।

10. उन बिंदुओं को ज्ञात कीजिए जिन पर $f(x)=(x-2{)}^4(x+1{)}^3$ द्वारा प्रदत्त फलन $f$ का, (i) स्थानीय उच्चतम बिंदु है (ii) स्थानीय निम्नतम बिंदु है (iii) नत परिवर्तन बिंदु है।

11. $f(x)={\cos }^{2}x+\sin x,x\in [0,\pi ]$ द्वारा प्रदत्त फलन $f$ का निरपेक्ष उच्चतम और निम्नतम मान ज्ञात कीजिए।

12. सिद्ध कीजिए कि एक $r$ त्रिज्या के गोले के अंतर्गत उच्चतम आयतन के लंब वृत्तीय शंकु की ऊँचाई $\frac{4r}{3}$ है।

13. मान लीजिए $[a,b]$ पर परिभाषित एक फलन $f$ है इस प्रकार कि सभी $x\in (a,b)$ के लिए $f^{\prime }(x)>0$ है तो सिद्ध कीजिए कि $(a,b)$ पर $f$ एक वर्धमान फलन है।

14. सिद्ध कीजिए कि एक $R$ त्रिज्या के गोले के अंतर्गत अधिकतम आयतन के बेलन की ऊँचाई $\frac{2\mathrm{R}}{\sqrt{3}}$ है। अधिकतम आयतन भी ज्ञात कीजिए।

15. सिद्ध कीजिए कि अर्द्धशीर्ष कोण $\alpha$ और ऊँचाई $h$ के लंब वृत्तीय शंकु के अंतर्गत अधिकतम आयतन के बेलन की ऊँचाई, शंकु के ऊँचाई की एक तिहाई है और बेलन का अधिकतम आयतन $\frac{4}{27}\pi h^3{\tan }^2\alpha$ है।

19 से 24 तक के प्रश्नों के सही उत्तर चुनिए।

16. एक $10\mathrm{m}$ त्रिज्या के बेलनाकार टंकी में $314{\mathrm{m}}^3/\mathrm{h}$ की दर से गेहूँ भरा जाता है। भरे गए गेहूँ की गहराई की वृद्धि दर है: (A) $1\mathrm{m}/\mathrm{h}$ (B) $0.1\mathrm{m}/\mathrm{h}$ (C) $1.1\mathrm{m}/\mathrm{h}$ (D) $0.5\mathrm{m}/\mathrm{h}$

सारांश

• यदि एक राशि $y$ एक दूसरी राशि $x$ के सापेक्ष किसी नियम $y=f(x)$ को संतुष्ट करते हुए परिवर्तित होती है तो $\frac{dy}{dx}($ या $f^{\prime }(x))x$ के सापेक्ष $y$ के परिवर्तन की दर को निरूपित करता है और ${\frac{dy}{dx}]}_{x=x_0}($ या $f^{\prime }\left(x_0\right))x=x_0$ पर) $x$ के सापेक्ष $y$ के निरूपित की दर को निरूपित करता है।

• यदि दो राशियाँ $x$ और $y,t$ के सापेक्ष परिवर्तित हो रही हों अर्थात् $x=f(t)$ और $y=g(t)$, तब शृंखला नियम से

$$\frac{dy}{dx}=\frac{dy}{dt}/\frac{dx}{dt},\text{ यदि }\frac{dx}{dt}\ne 0$$

• एक फलन $f$

(a) अंतराल $[a,b]$ में वर्धमान है यदि

$$[a,b]\text{ में }{x}_1<x_2\Rightarrow f\left(x_1\right)\le f\left(x_2\right)\text{, सभी }{x}_1,x_2\in (a,b)\text{ के लिए }$$

विकल्पतः यदि प्रत्येक $x\in [a,b]$ के लिए $f^{\prime }(x)\ge 0$, है।

(b) अंतराल $[a,b]$ में ह्रासमान है यदि

$$[a,b]\text{ में }{x}_1<x_2\Rightarrow f\left(x_1\right)\ge f\left(x_2\right)\text{, सभी }{x}_1,x_2\in (a,b)\text{ के लिए }$$

विकल्पतः यदि प्रत्येक $x\in [a,b]$ के लिए $f^{\prime }(x)\le 0$ है।

• फलन $f$ के प्रांत में एक बिंदु $c$ जिस पर या तो $f^{\prime }(c)=0$ या $f$ अवकलनीय नहीं है, $f$ का क्रांतिक बिंदु कहलाता है।

• प्रथम अवकलज परीक्षण मान लीजिए एक विवृत्त अंतराल I पर फलन $f$ परिभाषित है। मान लीजिए $\mathrm{I}$ में एक क्रांतिक बिंदु $c$ पर फलन $f$ संतत है तब

(i) जब $x$ बिंदु $c$ के बायीं ओर से दायीं ओर बढ़ता है तब $f^{\prime }(x)$ का चिह्न धन से ऋण में परिवर्तित होता है अर्थात् $c$ के बायीं ओर और पर्याप्त निकट प्रत्येक बिंदु पर यदि $f^{\prime }(x)>0$ तथा $c$ के दायीं ओर और पर्याप्त निकट प्रत्येक बिंदु पर यदि $f^{\prime }(x)<0$ तब $c$ स्थानीय उच्चतम का एक बिंदु है।

(ii) जब $x$ बिंदु $c$ के बायीं ओर से दायीं ओर बढ़ता है तब $f^{\prime }(x)$ का चिह्न ऋण से धन में परिवर्तित होता है अर्थात् $c$ के बायीं ओर और पर्याप्त निकट प्रत्येक बिंदु पर यदि $f^{\prime }(x)<0$ तथा $c$ के दायीं ओर और पर्याप्त निकट प्रत्येक बिंदु पर यदि $f^{\prime }(x)>$ 0 तब $c$ स्थानीय निम्नतम का एक बिंदु है।

(iii) जब $x$ बिंदु $c$ के बायीं ओर से दायीं ओर बढ़ता है तब $f^{\prime }(x)$ परिवर्तित नहीं होता है तब $c$ न तो स्थानीय उच्चतम का बिंदु है और न ही स्थानीय निम्नतम का बिंदु। वास्तव में इस प्रकार का बिंदु एक नति परिवर्तन बिंदु है।

• द्वितीय अवकलज परीक्षण मान लीजिए एक अंतराल I पर $f$ एक परिभाषित फलन है और $c\in \mathrm{I}$ है। मान लीजिए $f,c$ पर लगातार दो बार अवकलनीय है। तब

(i) यदि $f^{\prime }(c)=0$ और $f^{\prime \prime }(c)<0$ तब $x=c$ स्थानीय उच्चतम का एक बिंदु है। $f$ का स्थानीय उच्चतम मान $f(c)$ है।

(ii) यदि $f^{\prime }(c)=0$ और $f^{\prime \prime }(c)>0$ तब $x=c$ स्थानीय निम्नतम का एक बिंदु है। इस स्थिति में $f$ का स्थानीय निम्नतम मान $f(c)$ है।

(iii) यदि $f^{\prime }(c)=0$ और $f^{\prime \prime }(c)=0$, तब यह परीक्षण असफल रहता है।

इस स्थिति में हम पुनः वापस प्रथम अवकलज परीक्षण का प्रयोग करते हैं और यह ज्ञात करते हैं कि $c$ उच्चतम, निम्नतम या नति परिवर्तन का बिंदु है।

• निरपेक्ष उच्चतम और निरपेक्ष निम्नतम मानों को ज्ञात करने की व्यावहारिक विधि है:

चरण 1: अंतराल में $f$ के सभी क्रांतिक बिंदु ज्ञात कीजिए अर्थात् $x$ के वे सभी मान ज्ञात कीजिए जहाँ या तो $f^{\prime }(x)=0$ या $f$ अवकलनीय नहीं है।

चरण 2: अंतराल के अंत्य बिंदु लीजिए।

चरण 3: (चरण 1 व 2 से प्राप्त) सभी बिंदुओं पर $f$ के मानों की गणना कीजिए।

चरण 4: चरण 3 में गणना से प्राप्त $f$ के सभी मानों में से उच्चतम और निम्नतम मानों को लीजिए। यही उच्चतम मान, $f$ का निरपेक्ष उच्चतम मान और निम्नतम मान, $f$ का निरपेक्ष निम्नतम मान होंगे।