रासायनिक आबंधन तथा आण्विक संरचना CHEMICAL BONDING AND MOLECULAR STRUCTURE
द्रव्य एक या विभिन्न प्रकार के तत्त्वों से मिलकर बना होता है। सामान्य स्थितियों में उत्कृष्ट गैसों के अलावा कोई अन्य तत्त्व एक स्वतंत्र परमाणु के रूप में विद्यमान नहीं होता हैं। परमाणुओं के समूह विशिष्ट गुणों वाली स्पीशीज़ के रूप में विद्यमान होते हैं। परमाणुओं के ऐसे समूह को ‘अणु’ कहते हैं। प्रत्यक्ष रूप में कोई बल अणुओं के घटक परमाणुओं को आपस में पकड़े रहता है। विभिन्न रासायनिक स्पीशीज़ में उनके अनेक घटकों (परमाणुओं, आयनों इत्यादि) को संलग्न रखनेवाले आकर्षण बल को ‘रासायनिक आबंध’ कहते हैं। चूँकि रासायनिक यौगिक विभिन्न तत्त्वों के परमाणुओं की भिन्न-भिन्न विधिओं से संयुक्त होने के परिणामस्वरूप बनते हैं, अतः इससे कई प्रश्न उत्पन्न होते हैं। परमाणु संयुक्त क्यों होते हैं? केवल कुछ संयोजन ही संभव क्यों हैं? क्यों कुछ परमाणु संयुक्त होते हैं, जबकि कुछ अन्य ऐसा नहीं होते हैं? अणुओं की निश्चित आकृतियाँ क्यों होती हैं? इन सभी प्रश्नों के उत्तर देने के लिए समय-समय पर विभिन्न सिद्धांत सामने आए हैं। ये हैं कॉसेल-लूइस सिद्धांत, संयोजकता कक्ष इलेक्ट्रॉन युग्म प्रतिकर्षण (वी.एस.ई.पी.आर) सिद्धांत, संयोजकता आबंध सिद्धांत तथा आण्विक कक्षक सिद्धांत।
संयोजकता के विभिन्न सिद्धांतों का विकास तथा रासायनिक आबंधों की प्रकृति की व्याख्या का सीधा संबंध वास्तव में परमाणु-संरचना तत्त्वों के इलेक्ट्रॉनिक विन्यास तथा आवर्त सारणी को समझने से रहा है। प्रत्येक निकाय अधिक स्थायी होने का प्रयास करता है। यह आबंधन स्थायित्व पाने के लिए ऊर्जा को कम करने का प्राकृतिक तरीका है।
4.1 रासायनिक आबंधन की कॉसेल-लूइस अवधारणा
इलेक्ट्रॉनों द्वारा रासायनिक आबंधों के बनने की व्याख्या के लिए कई प्रयास किए गए, लेकिन सन् 1916 में कॉसेल और लुइस स्वतंत्र रूप से संतोषजनक व्याख्या देने में सफल हुए। उन्होंने सर्वप्रथम संयोजकता (Valence) की तर्क संगत व्याख्या की। यह व्याख्या उत्कृष्ट गैसों की अक्रियता पर आधारित थी।
लूइस परमाणुओं को एक धन आवेशित अष्टि (आंतरिक इलेक्ट्रॉन एवं नाभिकयुक्त) तथा बाह्य कक्षकों के रूप में निरूपित किया। बाह्य कक्षकों में अधिकतम आठ इलेक्ट्रॉन समाहित हो सकते हैं। उसने यह भी माना कि ये आठों इलेक्ट्रॉन घन के आठों कोनों पर उपस्थित होते हैं, जो केंद्रीय अष्टि को चारों तरफ से घेरे रहते हैं। इस प्रकार सोडियम के बाह्य कक्ष में उपस्थित एकल इलेक्ट्रॉन घन के एक कोने पर स्थित रहता है, जबकि उत्कृष्ट गैसों में घन के आठों कोनों पर एक-एक इलेक्ट्रॉन उपस्थित रहते हैं। इलेक्ट्रॉनों का यह अष्टक एक विशेष स्थायी विन्यास निरूपित करता है। लूइस ने यह अभिगृहीत दिया कि परमाणु परस्पर रासायनिक आबंध द्वारा संयुक्त होकर अपने स्थायी अष्टक को प्राप्त करते हैं। उदाहरण के लिए- सोडियम एवं क्लोरीन में सोडियम अपना एक इलेक्ट्रॉन क्लोरीन को सरलतापूर्वक देकर अपना स्थायी अष्टक प्राप्त करता है तथा क्लोरीन एक इलेक्ट्रॉन प्राप्त कर अपना स्थायी अष्टक निर्मित करता है, अर्थात् सोडियम आयन
लूइस प्रतीक : किसी अणु के बनने में परमाणुओं के केवल बाह्य कोश इलेक्ट्रॉन रासायनिक संयोजन में हिस्सा लेते हैं। ये इनके संयोजकता इलेकट्रॉन (Valence Electron) कहलाते हैं। आंतरिक कोश इलेक्ट्रॉन (Inner Shell Electron) अच्छी प्रकार से सुरक्षित होते हैं तथा सामान्यतः संयोजन प्रक्रिया में सम्मिलित नहीं होते हैं। एक अमेरिकी रसायनज्ञ जी.एन. लूइस ने परमाणु में संयोजकता इलेक्ट्रॉनों को निरूपित करने के लिए सरल संकेतनों को प्रस्तावित किया, जिन्हें लूइस प्रतीक (Lewis Symbol) कहा जाता है। उदाहरणार्थ- दूसरे आवर्त के तत्त्वों के ‘लूइस प्रतीक’ इस प्रकार हैं-
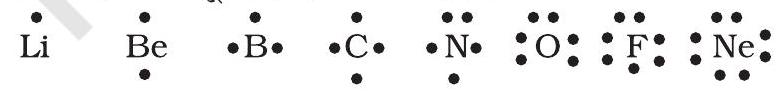
लूइस प्रतीकों का महत्त्व : प्रतीक के चारों ओर उपस्थित बिंदुओं की संख्या परमाणु के संयोजकता इलेक्ट्रॉनों की संख्या को दर्शाती है। यह संख्या तत्त्व की सामान्य अथवा समूह संयोजकता के परिकलन में सहायता देती है। तत्त्व की समूह संयोजकता या तो लूइस प्रतीक में उपस्थित बिंदुओं की संख्या के बराबर होती है या 8 में से बिंदुओं अथवा संयोजकता इलेक्ट्रॉनों की संख्या को घटाकर इसे परिकलित किया जा सकता है।
रासायनिक आबंधन के संबंध में कॉसेल ने निम्नलिखित तथ्यों की ओर ध्यान आकर्षित किया-
- आवर्त सारणी में उच्च विद्युत्-ऋणात्मकता वाले हैलोजेन तथा उच्च विद्युत्-धनात्मकता वाले क्षार धातु एक दूसरे से उत्कृष्ट गैसों द्वारा पृथक् रखे गए हैं।
- हैलोजेन परमाणुओं से ऋणायन तथा क्षार से धनायन का निर्माण संबंधित परमाणुओं द्वारा क्रमशः एक इलेक्ट्रॉन ग्रहण करने तथा एक इलेक्ट्रॉन मुक्त होने के फलस्वरूप होता है।
- इस प्रकार निर्मित ऋणायन तथा धनायन उत्कृष्ट गैस के स्थायी इलेक्ट्रॉनिक विन्यास को प्राप्त करते हैं। उत्कृष्ट गैसों में बाह्यतम कोश का आठ इलेक्ट्रॉनों वाला (अष्टक) विन्यास
- ऋणायन तथा धनायन स्थिर वैद्युत आकर्षण द्वारा स्थायित्व ग्रहण करते हैं।
उदाहरणार्थ- उपर्युक्त सिद्धांत के अनुसार, सोडियम तथा क्लोरीन से

धनायन तथा ऋणायन के बीच आकर्षण के फलस्वरूप निर्मित आबंध को ‘वैद्युत् संयोजक आबंध’ (Electrovalent Bond) का नाम दिया गया। इस प्रकार वैद्युत संयोजकता (Electrovalency) आयन पर उपस्थित आवेश की इकाइयों की संख्या के बराबर होती है। अतः कैल्सियम की धनात्मक वैद्युत संयोजकता दो हैं, जबकि क्लोरीन की ऋणात्मक संयोजकता एक है।
इलेक्ट्रॉन स्थानांतरण द्वारा आयन का बनना तथा आयनिक क्रिस्टलीय यौगिकों के बनने के बारे में आधुनिक संकल्पनाएँ कॉसेल की अभिगृहीतों (Postulates) पर आधारित हैं। आयनिक यौगिकों के व्यवहार को समझने तथा उनको क्रमबद्ध करने में कॉसेल के विचारों से उल्लेखनीय सहायता मिली। साथ ही साथ उन्होंने इस तथ्य को भी स्वीकार किया है कि अनेक यौगिक उनकी अवधारणाओं के अनुरूप नहीं थे।
4.1.1 अष्टक् नियम (Octet Rule)
सन् 1916 में कॉसेल तथा लूइस ने परमाणुओं के बीच रासायनिक संयोजन के एक महत्त्वपूर्ण सिद्धांत को विकसित किया। इसे ‘रासायनिक आबंधन का इलेक्ट्रॉनिकी सिद्धांत’ कहा जाता है। इस सिद्धांत के अनुसार, परमाणुओं का संयोजन संयोजक इलेक्ट्रॉनों के एक परमाणु से दूसरे परमाणु पर स्थानांतरण के द्वारा अथवा संयोजक इलेक्ट्रॉनों के सहभाजन (Sharing) के द्वारा होता है। इस प्रक्रिया में परमाणु अपने संयोजकता कोश में अष्टक प्राप्त करते हैं। इसे ‘अष्टक नियम’ कहते हैं।
4.1.2 सहसंयोजी आबंध
सन् 1919 में लैंगम्यूर ने लूइस अभिगृहीतिओं में संशोधन किया। उन्होंने स्थिर घनीय अष्टक की आवधारणा का परित्याग किया तथा ‘सहसंयोजक आबंध’ (Covalent Bond) का प्रयोग किया। लूइस-लैंगम्यूर के सिद्धांत को क्लोरीन अणु

दो क्लोरीन परमाणुओं के बीच सहसंयोजी आबंध
यहाँ बिंदु इलेक्ट्रॉनों को निरूपित करते हैं। ये संरचनाएँ ‘लूइस बिंदु संरचनाएँ’ कहलाती हैं।
अन्य अणुओं के लिए भी लूइस बिंदु संरचनाएँ लिखी जा सकती हैं, जिनमें संयुक्त होने वाले परमाणु समान अथवा भिन्न हो सकते हैं। इसके लिए मुख्य नियम निम्नलिखित हैं-
-
प्रत्येक आबंध का निर्माण परमाणुओं के मध्य एक इलेक्ट्रॉन युग्म के सहभाजन के फलस्वरूप होता है।
-
संयुक्त होने वाला प्रत्येक परमाणु सहभाजित युग्म में एक-एक इलेक्ट्रॉन का योगदान देता है।
-
इलेक्ट्रॉनों के सहभाजन के फलस्वरूप संयुक्त होने वाले परमाणु अपने बाहय कोश में उत्कृष्ट गैस विन्यास प्राप्त कर लेते हैं।
इस प्रकार, जल तथा कार्बन टेट्राक्लोराइड के अणुओं में आबंधों के निर्माण को हम इस प्रकार निरूपित कर सकते हैं-


कार्बन तथा चारो क्लोरीन परमाणुओं में से प्रत्येक, इलेक्ट्रान अष्टक प्राप्त करते हैं। एक इलेक्ट्रॉन युग्म द्वारा संयुग्मित दो परमाणु एकल सहसंयोजी आबंध (Single Covalent Bond) द्वारा आबंधित कहलाते हैं। कई यौगिकों में परमाणुओं के बीच बहु- आबंध (Multiple Bonds) उपस्थित होते हैं। बहु-आबधों का निर्माण दो परमाणुओं के मध्य एक से अधिक इलेक्ट्रॉन युग्मों के सहभाजन के फलस्वरूप होता है। दो परमाणुओं के मध्य यदि दो इलेक्ट्रॉन युग्मों का सहभाजन होता है, तो उनके बीच का सहसंयोजी आबंध ‘द्वि-आबंध’ (Double Bond) कहलाता है। उदाहरणार्थ- कार्बन डाइ- ऑक्साइड अणु में कार्बन तथा ऑक्सीजन परमाणुओं के मध्य दो द्वि-आबंध उपस्थित होते हैं।
इसी प्रकार एथीन (Ethene) के अणु में दो कार्बन परमाणु एक द्वि-आबंध द्वारा बंधित होते हैं।

जब संयोजी परमाणुओं के मध्य तीन इलेक्ट्रॉन युग्मों का सहभाजन होता है, जैसा


4.1.3 सरल अणुओं का लूइस निरूपण ( लूइस संरचाएँ )
लूइस बिंदु संरचनाओं द्वारा सहभाजित इलेक्ट्रॉन युग्मों तथा अष्टक नियम के अनुसार अणुओं एवं आयनों में आबंधन का चित्रण किया जाता है। यद्यपि यह चित्रण अणु में आबंधन तथा उसकी प्रकृति को पूर्ण रूप से स्पष्ट नहीं करता, परंतु इसके आधार पर अणु के विरचन (Formation) तथा उसके गुणों को पर्याप्त सीमा तक समझने में सहायता मिलती है। अतः अणुओं की लूइस बिंदु संरचनाएँ अत्यंत उपयोगी होती हैं। इन्हें निम्नलिखित पदों के आधार पर लिखा जा सकता है।
- लूइस संरचना लिखने के लिए आवश्यक कुल इलेक्ट्रॉनों की संख्या संयुग्मित होने वाले परमाणुओं के संयोजकताइलेक्ट्रॉनों के योग द्वारा प्राप्त की जाती है। उदाहरणार्थ
- संयोजकता इलेक्ट्रॉनों की कुल संख्या में ऋणायनों के लिए प्रति ऋणावेश एक इलेक्ट्रॉन जोड़ दिया जाता है, जबकि धनायनों के लिए प्रति धनावेश एक इलेक्ट्रॉन घटा दिया जाता है। उदाहरणार्थ-
- संयुक्त होने वाले परमाणुओं के रासायनिक प्रतीकों तथा अणु की आधारभूत संरचना (Skeletal Structure), अर्थात कौन से परमाणु किन परमाणुओं के साथ आबंधित हैं- इस बात का ज्ञान होने पर परमाणुओं के बीच सभी इलेक्ट्रॉनों का वितरण आबंधित सहभाजी इलेक्ट्रॉन युग्मों के रूप में तथा संपूर्ण आबंधों की संख्या के अनुपात में सरल हो जाता है।
- सामान्यतः अणु में न्यूनतम विद्युत् ऋणात्मकता वाला परमाणु केंद्रीय परमाणु का स्थान पाता है। हाइड्रोजन तथा फ्लुओरीन के परमाणु साधारणतया अंतस्थ स्थान (Terminal Position) पाते हैं। जैसे
- एकल आबंधों के लिए सहभाजित इलेक्ट्रॉन युग्म लिखने के पश्चात् शेष इलेक्ट्रॉन युग्मों का उपयोग या तो बहुआबंधन के लिए किया जाता है या वे एकाकी इलेक्ट्रॉन युग्मों के रूप में रहते हैं। आधारभूत आवश्यकता यह है कि प्रत्येक आबंधित परमाणु में इलेक्ट्रॉनों का ऑक्टेट
(अष्टक) पूरा हो जाए। कुछ अणुओं तथा आयनों की लूइस बिंदु संरचनाओं को सारणी 4.1 में दिया गया है।
सारणी 4.1 कुछ अणुओं तथा आयनों की लुइस संरचनाएँ
| अण/आयन | लूइस संरचना निरूपण | |
|---|---|---|
 |
||
 |
||
 |
- प्रत्येक
4.1.4 फॉर्मल आवेश
लूइस बिंदु संरचनाएँ सामान्यतः अणुओं की वास्तविक आकृति नहीं दर्शाती हैं। बहु-परमाणुक आयनों में संपूर्ण आवेश किसी विशेष परमाणु पर उपस्थित न होकर पूरे आयन पर स्थित होता है। हालाँकि प्रत्येक परमाणु पर फॉर्मल आवेश दर्शाया जा सकता है। बहुपरमाणुक अणु या आयन के किसी परमाणु पर उपस्थित फॉर्मल आवेश दर्शाया जा सकता है। बहुपरमाणुक अणु या आयन के किसी परमाणु पर उपस्थित फॉर्मल आवेश को उसके विगलित (Isolated) स्थिति (अर्थात् मुक्त परमाणु अवस्था) में संयोजकता इलेक्ट्रॉनों की कुल संख्या तथा लूइस संरचना में परमाणु को प्रदत्त इलेक्ट्रॉनों की संख्या के अंतर के रूप में परिभाषित किया जा सकता है। इसे इस प्रकार अभिव्यक्त किया जाता है-
फॉर्मल आवेश का परिकलन इस अवधारणा पर आधारित है कि अणु अथवा आयन में संबंधित परमाणु पर प्रत्येक सहभाजित युग्म में से एक इलेक्ट्रॉन तथा एकाकी युग्म के दोनों इलेक्ट्रॉन उपस्थित रहते हैं।
आइए, ओज़ोन

ऑक्सीजन के परमाणुओं को 1,2 तथा 3 द्वारा चिह्नित किया गया है-
- 1 द्वारा चिह्नित केंद्रीय
- 2 द्वारा चिह्नित अंतस्थ
- 3 द्वारा चिह्नित अंतस्थ
अतः

यहाँ पर ध्यान देने योग्य बात यह है कि फॉर्मल आवेश, अणु में वास्तविक आवेश पृथकन प्रकट नहीं करते हैं। लूइससंरचना में परमाणुओं पर आवेश को दर्शाने से अणु में संयोजकता इलेक्ट्रॉनों को लेखा-जोखा रखने में सहायता मिलती है। फॉर्मल आवेश की सहायता से किसी स्पीशीज़ की कई संभव लूइस संरचनाओं में से निम्नतम ऊर्जा की संरचना का चयन करने में सहायता मिलती है। साधारणतः न्यूनतम ऊर्जा वाली संरचना वह होती है, जिसके परमाणुओं पर न्यूनतम फॉर्मल आवेश हो। फॉर्मल आवेश का सिद्धांत आबंधन की शुद्ध सहसंयोजी प्रकृति पर आधारित है, जिसमें आबंधित परमाणुओं के मध्य इलेक्ट्रॉनों का सहभाजन समान रूप से होता है।
4.1.5 अष्टक नियम की सीमाएँ
यद्यपि अष्टक नियम अत्यंत उपयोगी है, परंतु यह सदैव लागू नहीं किया जा सकता है। यह मुख्य रूप से आवर्त सारणी के द्वितीय आवर्त के तत्त्वों पर लागू होता है तथा अधिकांश कार्बनिक यौगिकों की संरचनाओं को समझने में उपयोगी होता है। अष्टक नियम के तीन प्रमुख अपवाद हैं-
केंद्रीय परमाणु का अपूर्ण अष्टक
कुछ यौगिकों में केंद्रीय परमाणु के चारों ओर उपस्थित इलेक्ट्रॉनों की संख्या आठ से कम होती है। यह मुख्यतः उन तत्त्वों के यौगिकों में होता है, जिनमें संयोजकता इलेक्ट्रॉनों की संख्या चार से कम होती है। उदाहरण के लिए-
यहाँ पर
विषम इलेक्ट्रॉन (Odd-Electron) अणु
उन अणुओं जिनमें इलेक्ट्रॉनों की कुल संख्या विषम (Odd) होती है (जैसे-नाइट्रिक ऑक्साइड,
प्रसारित (Expanded) अष्टक
आवर्त सारणी के तीसरे तथा इसके आगे के आवर्तों के तत्त्वों में आबंधन के लिए
कक्षक भी उपलब्ध होते हैं। इन तत्त्वों के अनेक यौगिकों में केंद्रीय परमाणु के चारों ओर आठ से अधिक इलेक्ट्रॉन होते हैं। इसे प्रसारित अष्टक (Expanded Octet) कहते हैं। स्पष्ट है कि इन यौगिकों पर अष्टक नियम लागू नहीं होता है। ऐसे यौगिकों के कुछ उदाहरण हैं-
10 इलेक्ट्रॉन हैं।

अष्टक नियम की कुछ अन्य कमियाँ
- यह स्पष्ट है कि अष्टक नियम उत्कृष्ट गैसों की रासायनिक अक्रियता पर आधारित है, परंतु कुछ उत्कृष्ट गैसें (जैसे- ज़ीनॉन तथा क्रिप्टॉन) ऑक्सीजन तथा फ्लुओरीन से भी संयोजित होती हैं तथा कई यौगिक बनाती हैं। जैसे-
- अष्टक सिद्धांत अणु की आकृति स्पष्ट नहीं करता है।
- यह अणु की ऊर्जा, अर्थात् उसके सापेक्ष स्थायित्व के बारे में कुछ भी संकेत नहीं देता है।
4.2 आयनिक या वैद्युत् संयोजी आबंध
आयनिक आबंध विरचन की कॉसेल तथा लूइस अवधारणा से यह निष्कर्ष निकलता है कि इस आबंध का विरचन मुख्य रूप से निम्नलिखित तथ्यों निर्भर करेगा– उदासीन परमाणु से संबंधित धनायनों एवं ऋणायनों के बनने की सरलता तथा
- धनायनों एवं ऋणायनों की ठोस में व्यवस्थित होने की विधि, अर्थात् क्रिस्टलीय यौगिक का जालक (Lattice) निर्मित होने की विधि। धनायन का बनना आयनीकरण, अर्थात् उदासीन परमाणु में से एक या एक से अधिक इलेक्ट्रॉनों के निष्कासन द्वारा संपन्न होता है। इसी प्रकार उदासीन परमाणु द्वारा इलेक्ट्रॉन ग्रहण करने से ऋणायन प्राप्त होता है।
इलेक्ट्रॉन लब्धि एंथैल्पी,
यह स्पष्ट है कि आयनिक आबंध निम्न आयनन एंथैल्पी तथा अपेक्षाकृत निम्न इलेक्ट्रॉन लब्धि एंथैल्पी वाले तत्त्वों के बीच अधिक सरलता से बनते हैं।
अधिकांश आयनिक यौगिकों के धनायन धात्विक तत्त्वों से तथा ऋणायन अधात्विक तत्त्वों से निर्मित होते हैं। दो अधात्विक तत्त्वों से बनने वाला अमोनियम आयन एक अपवाद है। यह अनेक यौगिकों में धनायन के रूप में होता है।
आयनिक यौगिकों के क्रिस्टल में धनायन तथा ऋणायन त्रिविमीय रूप में नियमित रूप से व्यवस्थित रहते हैं। ये आयन कूलामी अन्योन्य (Coulombic Interaction) बलों द्वारा परस्पर जुड़े रहते हैं। आयनों के आकार उनके नियचन (Packing) क्रम तथा अन्य कारणों के आधार पर ये यौगिक विभिन्न क्रिस्टलीय संरचनाओं में क्रिस्टलित होते हैं। उदाहरण के लिए-सोडियम क्लोराइड,
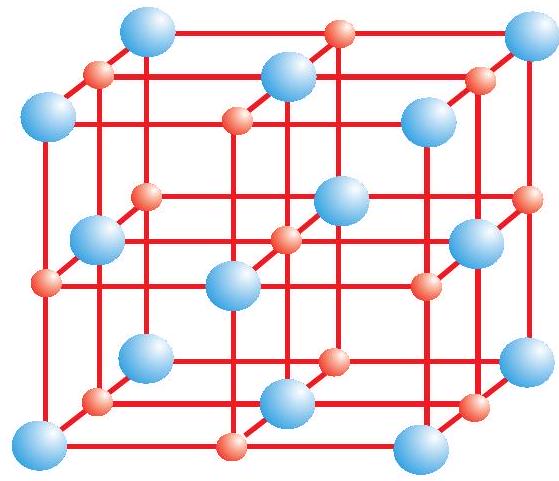
खनिज नमक संरचना
आयनिक ठोस के लिए इलेक्ट्रॉन लब्धि एंथैल्पी तथा आयनन एंथैल्पी का योग धनात्मक हो सकता है। ऐसे में क्रिस्टल संरचना का स्थायित्व उसके जालक के बनने में उत्पन्न मुक्त ऊर्जा के कारण होता है। उदाहरण के लिए
चूँकि आयनिक यौगिकों के विरचन में जालक एन्थैल्पी महत्त्वपूर्ण भूमिका निभाती है; अतः आइए, हम इस विषय में कुछ और जानकारी प्राप्त करें।
4.2.1 जालक एन्थैल्पी (जालक ऊर्जा)
किसी आयनिक ठोस के एक मोल यौगिक को गैसीय अवस्था में संघटक आयनों में पृथक करने के लिए आवश्यक ऊर्जा को उस यौगिक की ‘जालक एन्थैल्पी’ कहते है। उदाहरण के लिए-
इस प्रक्रिया में विपरीत आवेश वाले आयनों में आकर्षक बल तथा समान आवेश वाले आयनों में प्रतिकर्षण बल-दोनों भाग लेते हैं। चूँकि ठोस क्रिस्टल त्रिविभीय होता है, अत: केवल आकर्षण तथा प्रतिकर्षण बलों की अन्योन्य क्रिया से ही जालक एन्थैल्पी का परिकलन करना संभव नहीं है। क्रिस्टल ज्यामिति से संबंधित कारकों को भी इसमें सम्मिलित करना आवश्यक है।
4.3 आबंध प्राचल
4.3.1 आबंध लंबाई
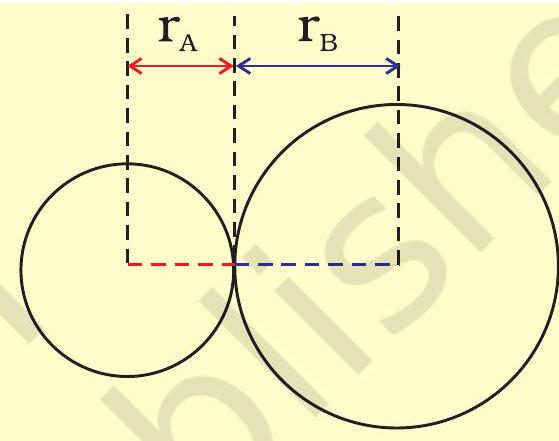
किसी अणु में आबंधित परमाणुओं के नाभिकों के बीच साम्यावस्था दूरी ‘आबंध लंबाई’ कहलाती है। आबंध लंबाई स्पेक्ट्रमी, एक्स-किरण विवर्तन तथा इलेक्ट्रॉन विवर्तन (Elec- tron Diffraction) विधियों की सहायता से ज्ञात की जाती है। इन तकनीकों का अध्ययन आप उच्च कक्षाओं में करेंगे। आबंधित युग्म का प्रत्येक परमाणु आबंध-लंबाई में योगदान देता है (चित्र 4.1)। सहसंयोजी आबंध में प्रत्येक परमाणु का योगदान उस परमाणु की ‘सहसंयोजी त्रिज्या’ कहलाती है।
आबंधित अवस्था में किसी परमाणु के क्रोड, जो संलग्न परमाणु के क्रोड के संपर्क में होता है, की त्रिज्या उसकी सहसंयोजी त्रिज्या मानी जाती है। सहसंयोजी त्रिज्या एक ही अणु में आबंधित दो समरूप परमाणुओं के बीच की
A
B
चित्र 4.1: सहसंयोजी अणु
दूरी का आधा भाग होती है। वांडरवाल त्रिज्या अनाबंधित अवस्था में संयोजी कोश सहित परमाणु का समग्र आकार निरूपित करती है। वांडरवाल त्रिज्या ठोस अवस्था में विभिन्न अणुओं के दो समरूप परमाणुओं के बीच की दूरी का आधा भाग होती है। क्लोरीन अणु के लिए सहसंयोजी तथा वांडर वाल त्रिज्याओं को चित्र 4.2 में दर्शाया गया है।
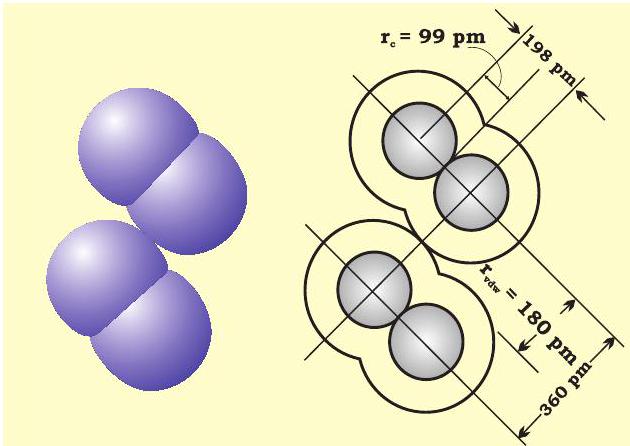
चित्र 4.2: क्लोरीन के अणु हेतु सहसंयोजी एवं वांडरवाल त्रिज्याएं। अंदर के वृत्त क्लोरीन के परमाणु का आकार इंगित करते हैं। (
कुछ एकल, द्वि तथा त्रि आबंधों की औसत लंबाइयाँ सारणी 4.2 में दी गई हैं; कुछ सामान्य अणुओं की आबंध लंबाइयाँ सारणी 4.3 में दी गई हैं, जबकि कुछ सामान्य तत्त्वों की सहसंयोजी त्रिज्याएँ सारणी 4.4 में क्रमबद्ध की गई हैं।
4.3.2 आबंध-कोण
किसी अणु के केंद्रीय परमाणु के आसपास उपस्थित आबंधन इलेक्ट्रॉन युग्म को धारण करने वाले ऑर्बिटलों के बीच बनने वाले कोण को ‘आबंध कोण’ कहते हैं। आबंध कोण को डिग्री के रूप में व्यक्त किया जाता है तथा प्रायोगिक तौर पर स्पेक्ट्रमी विधियों द्वारा ज्ञात किया जाता है। आबंध कोण अणु के केंद्रीय परमाणु के आसपास ऑर्बिटलों के वितरण की जानकारी देता है। अतः इससे हमें अणु/जटिल आयन की आकृति को ज्ञात करने में सहायता मिलती है। जैसे-जल के अणु में
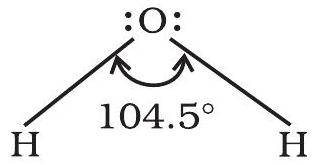
4.3.3 आबंध एन्थैल्पी
गैसीय स्थिति में दो परमाणुओं के बीच विशिष्ट आबंधों के एक मोल को तोड़ने के लिए आवश्यक ऊर्जा को ‘आबंध एन्थैल्पी’ कहते हैं। आबंध एन्थैल्पी का मात्रक
$$ \mathrm{H} {2}(\mathrm{~g}) \rightarrow \mathrm{H}(\mathrm{g})+\mathrm{H}(\mathrm{g}) ; \Delta{\mathrm{a}} \mathrm{H}^{\ominus}=435.8 \mathrm{~kJ} \mathrm{~mol}^{-1} $$
इसी प्रकार, बहुआबंधन वाले परमाणुओं (जैसे-
यह तथ्य महत्त्वपूर्ण है कि यदि आबंध विघटन एन्थैल्पी अधिक है, तो आबंध अधिक प्रबल होगा।
बहुपरमाणुक अणुओं में आबंध-सामर्थ्य का निर्धरण अधिक जटिल होता है। उदाहरणार्थ-
| आबंध का प्रकार | सहसंयोजी आबंध लंबाई |
|---|---|
| 96 | |
| 107 | |
| 136 | |
| 143 | |
| 143 | |
| 154 | |
| 121 | |
| 122 | |
| 133 | |
| 138 | |
| 116 | |
| 120 |
| 37 | |||||||
|---|---|---|---|---|---|---|---|
| 74 (1) | O | F | 64 | ||||
| 99 | |||||||
| P | 110 | 114 | |||||
| As | 121 | 104 | I | 133 | |||
| 141 | 137 |
सारणी 4.3 कुछ सामान्य अणुओं की आबंध लंबाइयाँ
| अणु | आबंध लंबाई (pm) |
|---|---|
| 74 | |
| 144 | |
| 199 | |
| 228 | |
| 267 | |
| 109 | |
| 121 | |
| 92 | |
| 127 | |
| 141 | |
| 160 |
सारणी 4.4 सह संयोजी त्रिज्याएँ*
- दिए गए मान एकल आबंधों के लिए हैं। अन्य प्रकार के आबंधों को कोष्ठक में दर्शाया गया है। (आवर्ती प्रवृत्ति के लिए एकक 3 भी देखें) $\mathrm{H} {2} \mathrm{O}(\mathrm{g}) \rightarrow \mathrm{H}(\mathrm{g})+\mathrm{OH}(\mathrm{g}) ; \Delta{\mathrm{a}} \mathrm{H} _{1}^{\ominus}=502 \mathrm{~kJ} \mathrm{~mol}^{-1}$
उदाहरण के लिए- जल अणु में
4.3.4 आबंध कोटि
सहसंयोजी आबंध की लूइस व्याख्या के अनुसार किसी अणु में दो परमाणुओं के मध्य आबंधों की संख्या आबंध कोटि (Bond Order) कहलाती है। उदाहरण के लिए-
समइलेक्ट्रॉनी अणुओं तथा आयनों में आबंध कोटि समान होती है। उदाहरण के लिए-
इसी प्रकार
4.3.5 अनुनाद संरचनाएँ
प्रायोगिक निर्धारित प्राचलों (Parameters) के संदर्भ में किसी अणु के निरूपण के लिए एक लूइस-संरचना कई बार पर्याप्त नहीं होती है। उदाहरणार्थ- ओज़ोन अणु को निम्नलिखित
संरचनाओं (I व II) द्वारा समान रूप से निरूपित किया जा सकता है-

III
चित्र
दोनों ही संरचनाओं में एक
सामान्य रूप से यह कहा जा सकता है कि
- अनुनाद अणु को स्थायित्व प्रदान करता है, क्योंकि अनुनाद संकर की ऊर्जा किसी भी विहित संरचना की ऊर्जा से कम होती है।
- अनुनाद के कारण आबंधों के लक्षण औसत मान प्राप्त करते हैं। इस प्रकार
अनुनाद संकल्पना से संबंधित कई भ्राँतिया हैं, जिनका निवारण आवश्यक है। आपको स्मरण रहे कि-
- वास्तव में विहित संरचनाओं का कोई अस्तित्त्व नहीं होता है।
- ऐसा नहीं होता कि अणु कुछ समय के लिए किसी विहित संरचना के रूप में उपस्थित रहता है, जबकि अन्य समय किसी दूसरी विहित संरचना को अपनाता है।
- विहित संरचनाओं में चलावयवों (कीटो तथा इनॉल) के मध्य पाए जाने वाले साम्य जैसा कोई साम्य नहीं होता है।
- वास्तविक रूप में अणु की केवल एक संरचना होती है, जो विहित संरचनाओं की अनुनाद संकर होती है। उसे केवल एक लूइस संरचना द्वारा प्रदर्शित नहीं किया जा सकता है।
4.3.6 आबंध-ध्रुवणता
किसी आबंध का सौ प्रतिशत आयनिक या सहसंयोजी होना एक आदर्श स्थिति है। परंतु वास्तव में कोई भी आबंध या यौगिक पूर्ण रूप से सहसंयोजी या आयनिक नहीं होता है। यहाँ तक कि दो हाइड्रोजन परमाणुओं के बीच बनने वाले सहसंयोजी आबंध की प्रकृति भी आंशिक रूप से आयनिक होती है।
जब सह संयोजी आबंध दो समान परमाणुओं के बीच, ( जैसे-
ध्रुवण के कारण ऐसे अणु में द्विध्रुव आघूर्ण (Dipole Moment) उत्पन्न हो जाता है। द्विध्रुव को आवेश के मान तथा धनात्मक और ॠणात्मक आवेशों के बीच की दूरी के गुणनफल के रूप में परिभाषित किया जाता है। इसे सामान्यत: ग्रीक शब्द ’

द्विध्रुव आघूर्ण
द्विध्रुव आघूर्ण को सामान्यतः डिबाए (Debye) मात्रक (D) के रूप में व्यक्त किया जाता है।
जहाँ पर
इसके अलावा द्विध्रुव आघूर्ण एक सदिश राशि है। परंपरा के अनुसार इसे एक छोटे तीर द्वारा दर्शाया जाता है, जिसका पुच्छल सिरा ऋणात्मक केंद्र पर स्थित होता है तथा अग्र सिरा घनात्मक केंद्र की ओर उन्मुख रहता है। परंतु रसायन में द्विध्रुव आघूर्ण की उपस्थिति अणु की लूइस संरचना के उपर क्रॉस तीर
यह तीर अणु में इलेक्ट्रॉन घनत्व के बदलाव की दिशा बतलाता है। ध्यान दीजिए की क्रॉस तीर की दिशा द्विध्रुव आघूर्ण के सदिश की पारम्परिक दिशा के विपरीत है।
बहुपरमाणुक अणुओं में द्विध्रुव आघूर्ण केवल आबंधों के अपने द्विध्रुव, जिन्हें ‘आबंध आघूर्ण’ कहा जाता है, पर ही निर्भर नहीं करता, अपितु यह विभिन्न आबंधों की स्थानिक व्यवस्था पर भी निर्भर करता है। ऐसे में द्विध्रुव अणु के विभिन्न आबंधों के द्विध्रुव आघूर्ण अणु के विभिन्न आबंधों के द्विध्रुव आघूर्णो का सदिश-योग (Vector sum) होता है। उदाहरण के लिए- जल के अणु, जिसकी आकृति बंकित होती है, के दो

(क)
आबंध द्विध्रुर्ण

(ख) परिणामी द्विध्रुव आघूर्ण
कुल द्विध्रुव आघूर्ण,

(क)
(ख)
आइए,
इसलिए है कि


जिस प्रकार सहसंयोजी आबंध में आंशिक आयनिक लक्षण होता है, उसी प्रकार आयनिक आबंध में भी आंशिक सहसंयोजी लक्षण होता है। आयनिक आबंधों के आंशिक सहसंयोजी लक्षण की विवेचना फाजान्स (Fajans) ने निम्नलिखित नियमों के अनुसार की-
- धनायन के आकार के घटने तथा ऋणायन के आकार के बढ़ने पर आयनिक आबंध के सहसंयोजी लक्षण में वृद्धि होती है।
- धनायन तथा ऋणायन पर आवेश की मात्रा बढ़ने से आयनिक आबंध के सहसंयोजी लक्षण में वृद्धि होती है।
- समान आकार तथा आवेश के धनायनों में से उस धनायन की ध्रुवण-क्षमता अपेक्षाकृत अधिक होती है, जिसका इलेक्ट्रॉनिक विन्यास क्षार तथा क्षारीय मृदा धातुओं के धनायनों के उत्कृष्ट गैस विन्यास
सारणी 4.5 कुछ चयनित अणुओं के द्विध्रुव-आघूर्ण
| अणु का प्रकार (AB) | उदाहरण | द्विध्रुव-आघूर्ण | आकृति |
|---|---|---|---|
| 1.78 | रैखिक | ||
| 1.07 | रैखिक | ||
| 0.79 | रैखिक | ||
| 0.38 | रैखिक | ||
| 0 | रैखिक | ||
| 1.85 | मुड़ा | ||
| 0.95 | मुड़ा | ||
| 0 | रैखिक | ||
| 1.47 | त्रिसमनतताक्ष-पिरामिड पिरामिड | ||
| 0.23 | त्रिसमनताक्ष-समतल | ||
| 0 | चतुष्फलकीय | ||
| चतुष्फलकीय | |||
| 1.04 | चतुष्फलकीय |
4.4 संयोजकता कोश इलेक्ट्रॉन युग्म प्रतिकर्षण सिद्धांत
जैसा पहले बताया गया है, लूइस अवधारणा अणुओं की आकृति की व्याख्या में असमर्थ है। वी. एस. ई. पी. आर. सिद्धांत सहसंयोजी आकृति को समझने के लिए एक सरल कार्यविधि उपलब्ध कराता है। यह विधि सर्वप्रथम सन् 1940 में सिजविक तथा पॉवेल (Sidgwick and Powell) ने परमाणुओं के संयोजकता कोश में उपस्थित इलेक्ट्रॉन युग्मों के बीच प्रतिकर्षण अन्योग्य क्रियाओं के आधार पर प्रतिपादित की थी। इस विधि को नाइहोम तथा गिलेस्पी (Nyholm and Gillespie) ने सन् 1957 में और अधिक विकसित तथा संशोधित किया।
वी. एस. ई. पी. आर. सिद्धांत की मूलभूत धारणाएँ हैं-
- अणु की आकृति, केंद्रीय परमाणु के आसपास उपस्थित संयोजीकोश इलेक्ट्रॉन युग्मों (संयोजित अथवा असंयोजित) की संख्या पर निर्भर करती है।
- केंद्रीय परमाणु के संयोजकता कोश में उपस्थित इलेक्ट्रॉन युग्म एक-दूसरे को प्रतिकर्षित करते हैं, क्योंकि उनके इलेक्ट्रॉन अभ्र (Electron Cloud) पर ऋणात्मक आवेश होता है।
- ये इलेक्ट्रॉन युग्म त्रिविम में उन स्थितियों में अवस्थित होने का प्रयत्न करते हैं, जिसके फलस्वरूप उनमें प्रतिकर्षण कम से कम हो। इस स्थिति में उनके मध्य अधिकतम दूरी होती है।
- संयोजकता-कोश को एक गोले के रूप में माना जाता है तथा इलेक्ट्रॉन युग्म गोलीय (Spherical) सतह पर एक दूसरे से अधिकतम दूरी पर स्थित होते हैं।
- बहुआबंध को एक एकल इलेक्ट्रॉन युग्म के रूप में तथा इस बहुआबंध के दो या तीन इलेक्ट्रॉन युग्मों को एकल सुपर युग्म समझा जाता है।
- यदि अणु को दो या अधिक अनुनाद संरचनाओं द्वारा दर्शाया जा सके, तो इस स्थिति में वी. एस. ई. पी. आर मॉडल ऐसी प्रत्येक संरचना पर लाग होता है।
इलेक्ट्रॉन युग्मों के बीच प्रतिकर्षण अन्योन्य क्रियाएँ निम्नलिखित क्रम में घटती हैं-
एकाकी युग्म - एकाकी युग्म > एकाकी युग्म - आबंधी युग्म > (lp) (lp) (lp) (lp)
आबंधी युग्म - आबंधी युग्म
(bp) (bp) नाईहोम तथा गिलेस्पी ने इलेक्ट्रॉनों के एकाकी युग्मों तथा आबंधी युग्मों के महत्त्वपूर्ण अंतरों की व्याख्या करते हुए वी. एस. ई. पी. आर. मॉडल में सुधार किया। एकाकी इलेक्ट्रॉन युग्म केंद्रीय परमाणु पर स्थानगत (Localised) होते हैं, जबकि प्रत्येक आबंधी युग्म दो परमणुओं के बीच सहभाजित होता है। अतः किसी अणु में आबंधी इलेक्ट्रॉन युग्म की अपेक्षा एकाकी युग्म अधिक स्थान घेरते हैं। इसके फलस्वरूप एकाकी इलेक्ट्रॉन युग्मों के बीच एकाकी युग्म-आबंधी युग्म तथा आबंधी युग्मआबंधी युग्म की अपेक्षा अधिक प्रतिकषर्ण होता है। इन प्रतिकर्षणप्रभावों के कारण अणु की संभावित आकृति में भिन्नता होती है तथा अणु के आबंध कोणों में भी अंतर आ जाता है।
वी. एस. ई. पी. आर. मॉडल की सहायता से अणुओं की ज्यामितीय आकृतियों का पूर्वानुमान लगाने के लिए अणुओं को दो श्रेणियों में बाँटा जाता है-
(i) वे अणु, जिनके केंद्रीय परमाणु पर कोई भी एकाकी युग्म उपस्थित नहीं होता है।
(ii) वे अणु, जिनके केंद्रीय परमाणु पर एक या एक से अधिक एकाकी युग्म उपस्थित होते हैं।
सारणी 4.6 में एकाकी युग्मरहित केंद्रीय परमाणु
जैसा सारणी 4.6 में दर्शाया गया है,
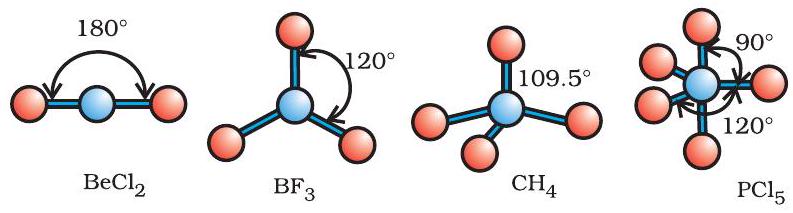
चित्र 4.8 बिना एकाकी युग्म वाले केंद्रीय परमाणु युक्त अणुओं की आकृतियाँ
सारणी 4.6 एकाकी युग्मरहित केंद्रित परमाणु युक्त अणुओं की ज्यामिति
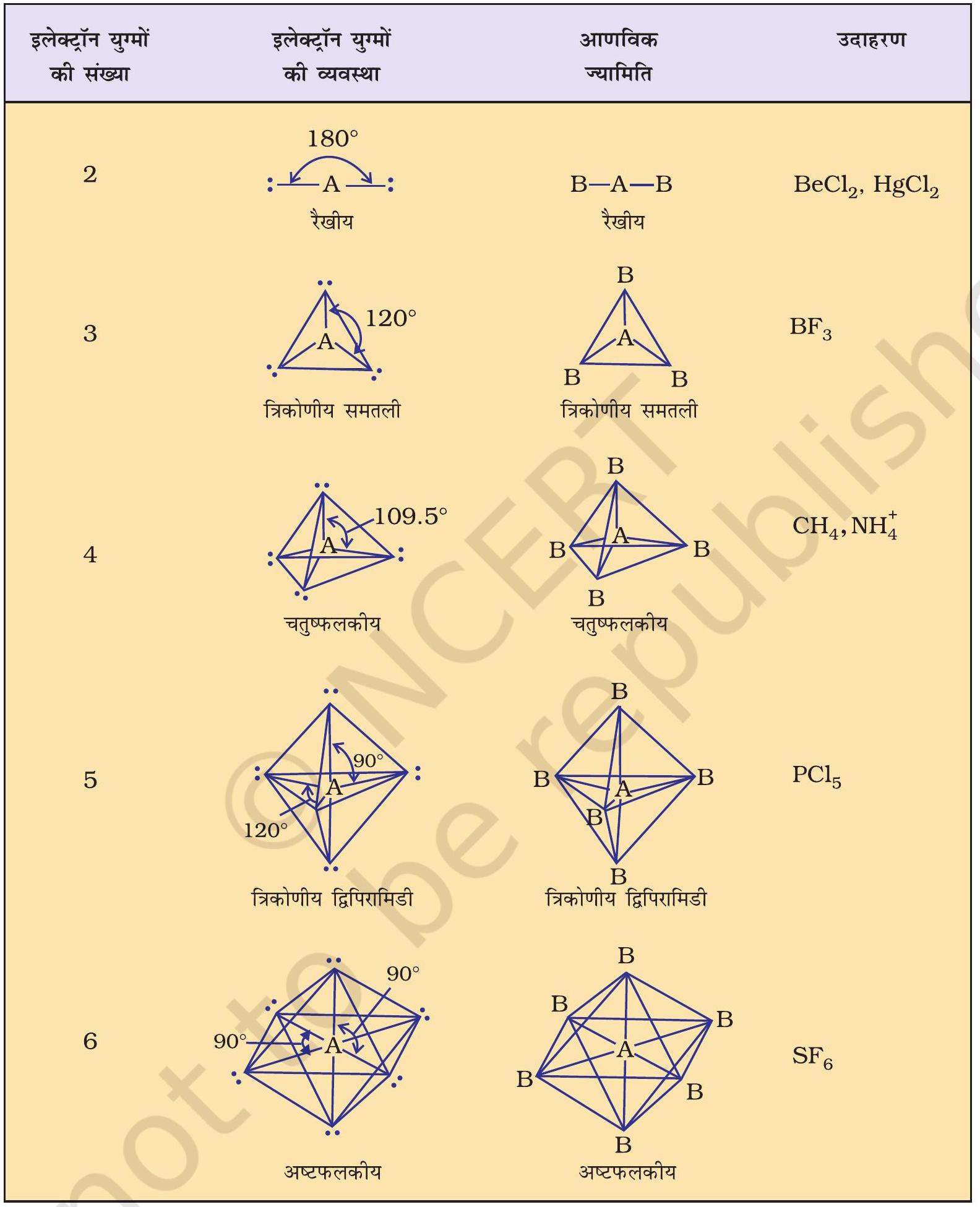
- धूसर रेखाओं का उपयोग केवल संपूर्ण आकृति को दर्शाने के लिए किया गया है; ये आबंधों को नहीं दर्शाती हैं।
सारणी 4.7 कुछ सरल अणुओं/आयनों की आकृतियाँ (ज्यामिति), जिनके केंद्रीय परमाणु पर एक या एक से अधिक एकाकी इलेक्ट्रॉन युग्म उपस्थित हैं।
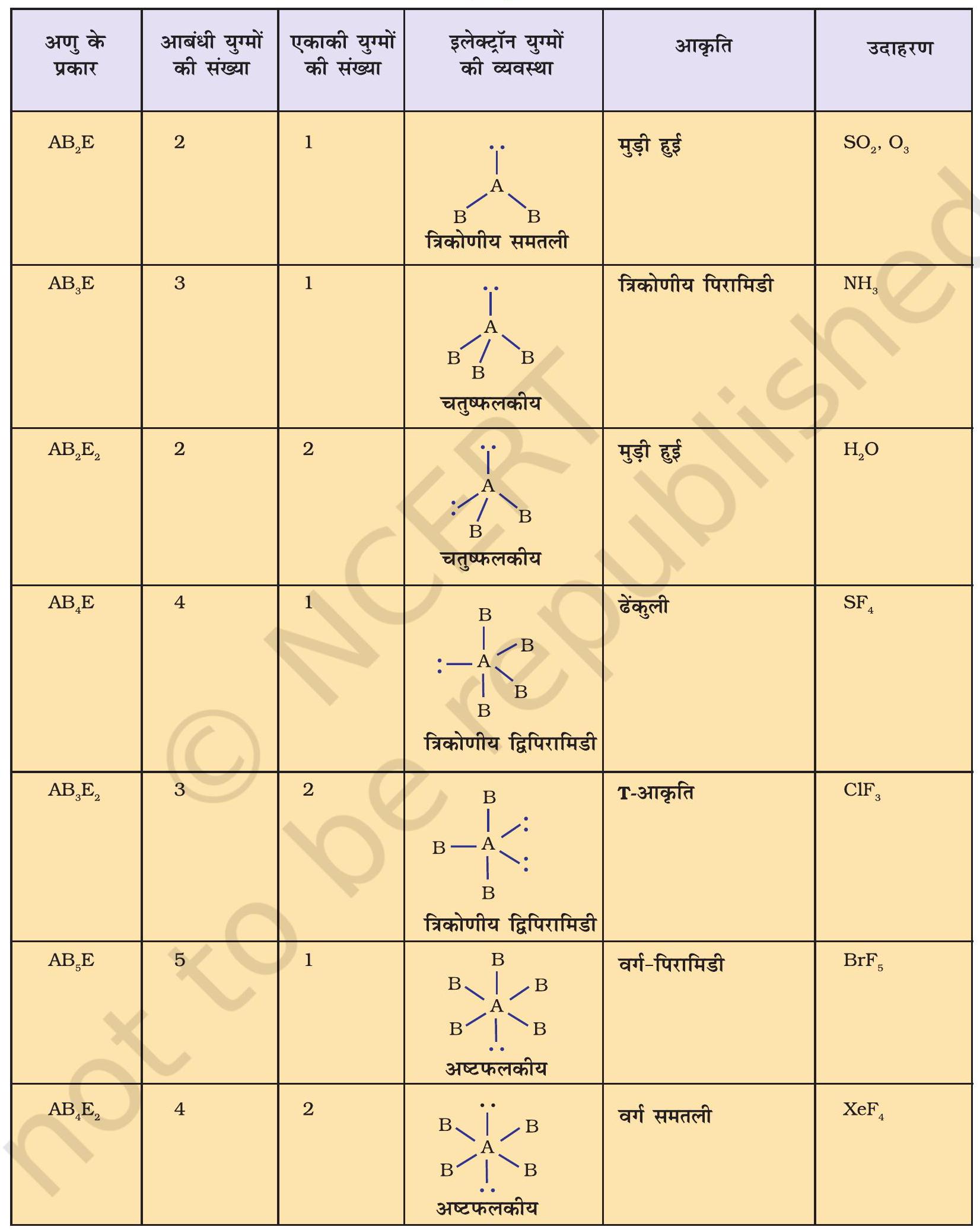
सारणी 4.8 आबंधी-युग्म तथा एकाकी युग्म वाले कुछ अणुओं की आकृति
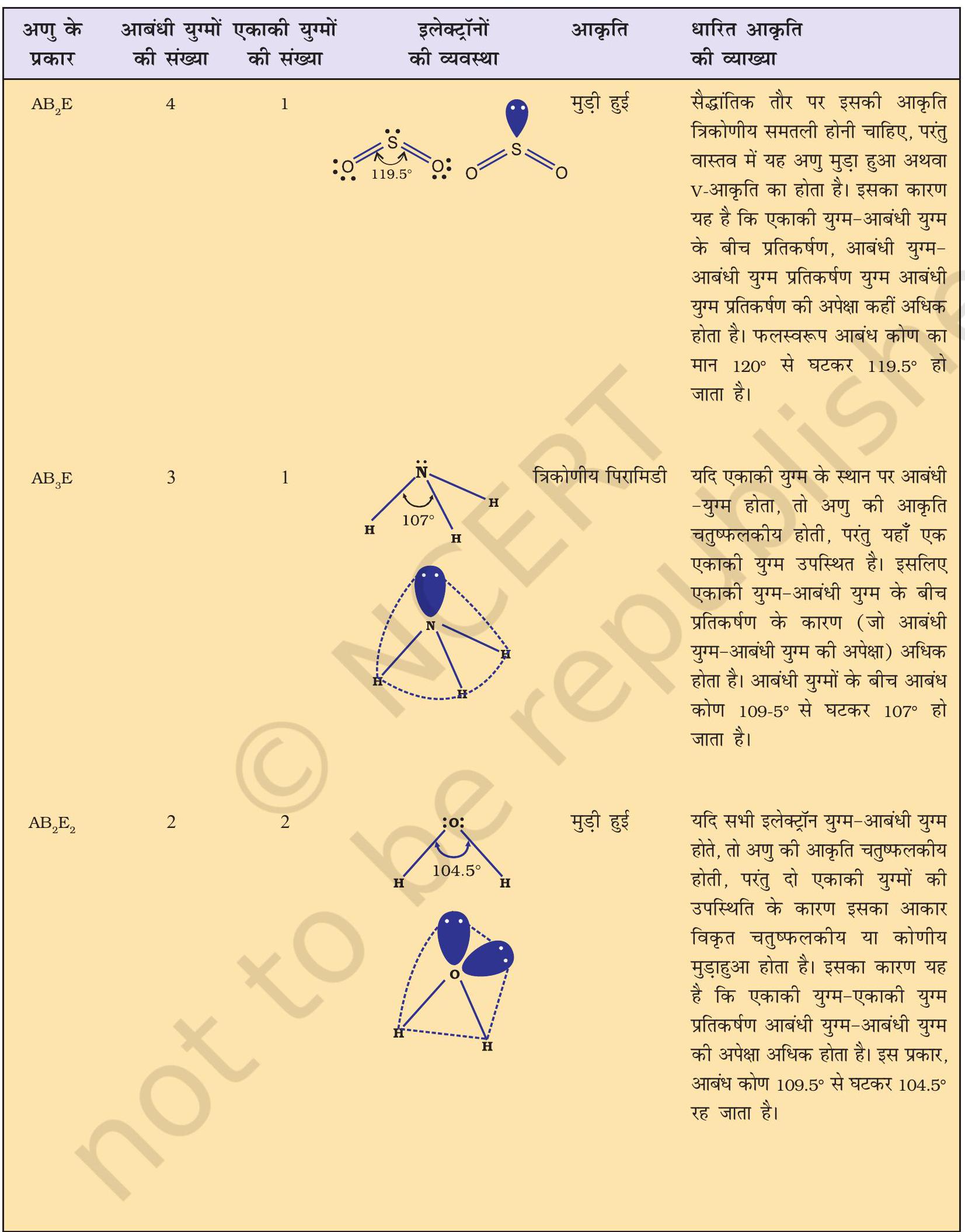
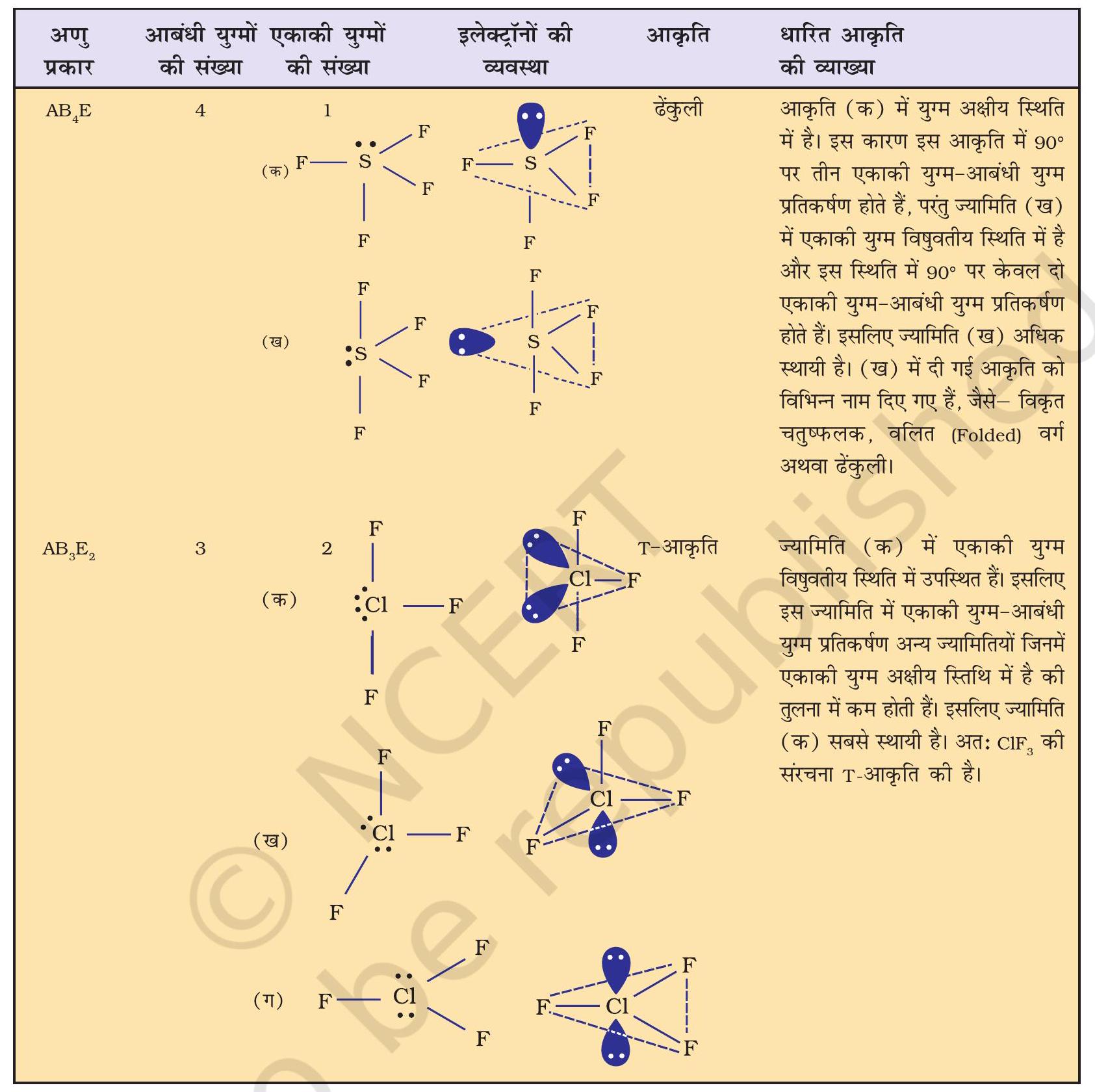
वी. एस. ई. पी. आर. मॉडल की सहायता से अनेक अणुओं, विशेष रूप से
4.5 संयोजकता आबंध सिद्धांत
जैसा आप जानते हैं लूइस अवधारणा से अणुओं की संरचनाओं को लिखने में सहायता मिलती है, परंतु रासायनिक आबंध बनने की व्याख्या करने में यह असमर्थ है। उक्त अवधारणा यह भी स्पष्ट नहीं करती कि अणुओं की आबंध वियोजन ऊर्जाएँ (Bond Dissociation Energies) तथा आबंध लंबाइयाँ जैसे -
संबंधित परमाणुओं के बीच एक इलेक्ट्रॉन युग्म के सहभाजन के फलस्वरूप एकल सहसंयोजी आबंध बनता है। यह मॉडल बहुपरमाणुक अणुओं की आकृतियों की विभिन्नता पर भी प्रकाश नहीं डालता।
इसी प्रकार वी. एस. ई. पी. आर. सिद्धांत सरल अणुओं की आकृति के बारे में जानकारी देता है, परंतु यह उनकी व्याख्या नहीं कर सकता था। इसका उपयोग भी सीमित है। इन कमियों को दूर करने के लिए दो महत्त्वपूर्ण सिद्धांतों का प्रतिपादन किया गया है, जो क्वांटम यांत्रिकी (Quantum Mechanical) सिद्धांत पर आधारित हैं। ये सिद्धांत हैसंयोजकता आबंध सिद्धांत तथा अणु-कक्षक सिद्धांत (Molecular Orbital Theory)।
संयोजकता आबंध सिद्धांत को सर्वप्रथम हाइटलर तथा लंडन (Heitler and London) ने सन् 1927 में प्रस्तुत किया था, जिसका विकास पॉलिंग (Pauling) तथा अन्य वैज्ञानिकों ने बाद में किया। इस सिद्धांत का विवेचन परमाणु कक्षकों, तत्त्वों के इलेक्ट्रॉनिक विन्यासों (इकाई 2), परमाणु कक्षकों के अतिव्यापन और संकरण तथा विचरण (Variation) एवं अध्यारोपण (Superposition) के सिद्धांतों के ज्ञान पर आधारित है। इन सभी पहलुओं के परिपेक्ष्य में संयोजकता आबंध सिद्धांत का गूढ़ विवेचन इस पुस्तक की विषय-वस्तु से बाहर है। अत: इस सिद्धांत का वर्णन केवल गुणात्मक दृष्टि से तथा गणित का उपयोग किए बिना ही किया जाएगा। आइए, प्रारंभ में सरलतम अणु,
मान लीजिए कि हाइड्रोजन के दो परमाणु
(i) एक परमाणु के नाभिक तथा उसके इलेक्ट्रॉनों के बीच
(ii) एक परमाणु के नाभिक तथा दूसरे परमाणु के इलेक्ट्रॉनों के बीच
इसी प्रकार प्रतिकर्षण बल निम्नलिखित में उत्पन्न होते हैं-
(i) दो परमाणुओं के इलेक्ट्रॉनों के बीच
(ii) दो परमाणुओं के नाभिकों के बीच 
प्रतिकर्षण बल
चित्र
आकर्षण बल दोनों परमाणुओं को एक-दूसरे के पास लाते हैं, जबकि प्रतिकर्षण बल उन्हें दूर करने का प्रयास करते हैं (चित्र 4.7)।
प्रायोगिक तौर पर यह पाया गया है कि नए आकर्षण बलों का मान नए प्रतिकर्षण बलों के मान से अधिक होता है। इसके परिणाम- स्वरूप दोनों परमाणु एक-दूसरे के करीब आते हैं तथा उनकी स्थितिज ऊर्जा कम हो जाती है। अंततः ऐसी स्थिति है, नेट आकर्षण बल तथा प्रतिकर्षण बल के बराबर हो जाता है और निकाय की ऊर्जा न्यून स्तर पर पहुँच जाती है। इस अवस्था में हाइड्रोजन के परमाणु ‘आबंधित’ कहलाते हैं और एक स्थायी अणु बनाते हैं, जिसकी आबंध लंबाई
चूँकि हाइड्रोजन के दो परमाणुओं के बीच आबंध बनने पर ऊर्जा मुक्त होती है, इसलिए हाइड्रोजन अणु दो पृथक् परमाणुओं की अपेक्षा अधिक स्थायी होता है। इस प्रकार मुक्त ऊर्जा ‘आबंध एंथैल्पी’ कहलाती है। यह चित्र 4.8 में दिए गए
आरेख में न्यूनतम के संगत होती है। विलोमतः
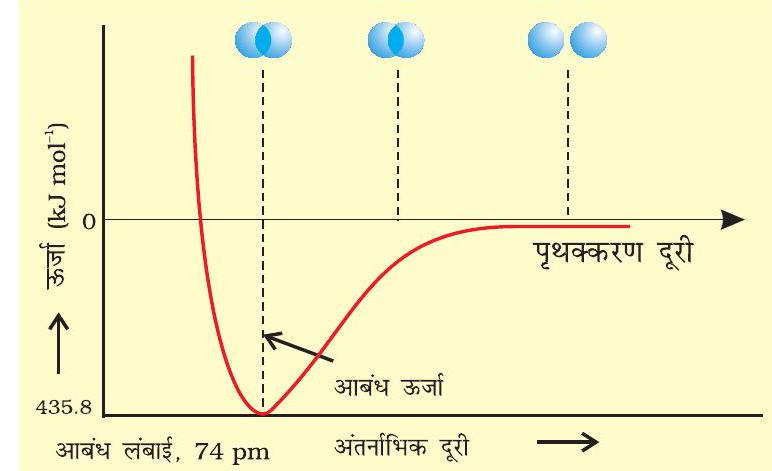
चित्र 4.8:
4.5.1 कक्षक अतिव्यापन अवधारणा
हाइड्रोजन अणु के विरचन में इस अवस्था में न्यूनतम ऊर्जा अवस्था प्राप्त होती है। इस अवस्था में दो परमाणु इतने करीब हो जाते हैं कि उनके परमाणु-कक्षक आंशिक रूप से अंतरभेदन ‘परमाणु-कक्षक अतिव्यापन’ कहलाता है। इसके परिणामस्वरूप इलेक्ट्रॉन संयुग्मित होते हैं। अतिव्यापन की सीमा सहसंयोजी आबंध की प्रबलता को निर्धारित करती है। सामान्यतः अधिक अतिव्यापन दो परमाणुओं के बीच प्रबल आबंध बनाने से संबंधित है। इस प्रकार, कक्षक अतिव्यापन अवधारणा के अनुसार दो परमाणुओं के बीच सहसंयोजी आबंध का बनना संयोजकता कक्ष में उपस्थित विपरीत चक्रण (Spin) वाले इलेक्ट्रॉनों के संयुग्मन के परिणामस्वरूप होता है।
4.5.2 आबंधों के दिशात्मक गुणधर्म
जैसा आप जानते हैं, सहसंयोजी आबंध परमाणु कक्षकों के अतिव्यापन से बनते हैं। उदाहरण के लिए- हाइड्रोजन का अणु बनने में इसके दो परमाणुओं के संयोजन में उनके
‘संयोजकता आबंध सिद्धांत’ के आधार पर
4.5.3 परमाणु कक्षकों का अतिव्यापन
जब दो परमाणु आबंध विचरण के लिए पास आते हैं, तब उनके कक्षकों का अतिव्यापन धनात्मक, ॠणात्मक या शून्य हो सकता है। यह ऑर्बिटल तरंग फलन के आयाम (amplitude) की दिक्स्थान (स्पेस) में दिशा और चिह्न (फ़ेज़) पर निर्भर करता है (चित्र 4.9)। सीमा- सतह आरेखों पर दर्शाए गए धनात्मक और ऋणात्मक चिह्न तरंग फलन का चि्न (फ़ेज़) बतलाते हैं। इनका आवेश से कोई संबंध नहीं होता। आबंध बनाने के लिए ऑर्बिटलों का चिह्न (फ़ेज़) और अभिविन्यास एक समान होना चाहिए। इसे धनात्मक अतिव्यापन कहते हैं।

(a)

(b)

शून्य अतिव्यापन (एक दूसरे की
ओर पहुँचने की दिशा में अभिविन्यास
अलग होने के कारण अतिव्यापन नहीं होता )

चित्र

(e)

(f)

(h)
शून्य अतिव्यापन
सहसंयोजी आबंध के विरचन के मुख्य कारक के रूप में अतिव्यापन की कसौटी समनाभिकीय विषमनाभिकीय द्विपरमाणुक अणुओं तथा बहुपरमाणुक अणुओं पर समान रूप से लागू होता है। हम जानते हैं कि
आइए, सर्वप्रथम हम मेथेन
4.5.4 अतिव्यापन के प्रकार तथा सहसंयोजी आबंध की प्रकृति
कक्षकों के अतिव्यापन के प्रकार के आधार पर सहसंयोजी आबंध के दो प्रकार होते हैं-
(i) सिग्मा
(
(i) सिग्मा (



(ii) पाई

4.5.5 सिग्मा तथा पाई आबंधों की प्रबलता
मूलतः आबंध की प्रबलता अतिव्यापन की सीमा पर निर्भर करती है। सिग्मा आबंध में कक्षकों का अतिव्यापन अधिक होता है। इसलिए सिग्मा आबंध, पाई आबंध (जिसमें कम अतिव्यापन होता है) की तुलना में अधिक प्रबल होता है। इसके अलावा यह जानना भी महत्त्वपूर्ण है कि दो परमाणुओं के बीच पाई आबंध कभी अकेला नहीं पाया जाता है। यह सदैव सिग्मा आबंध के साथ ही होता है। यह सदैव उन अणुओं में पाया जाता है, जिनमें द्विआबंध या त्रिआबंध उपस्थित होते हैं।
4.6 संकरण
संकरण के महत्त्वपूर्ण लक्षण- संकरण के मुख्य लक्षण इस प्रकार हैं-
- संकर कक्षकों की संख्या संकरण की प्रक्रिया में भाग लेने वाले कक्षकों की संख्या के बराबर होती है।
- संकर कक्षक सदैव समान ऊर्जा तथा आकार के होते हैं।
- संकर कक्षक स्थायी आबंध बनाने में शुद्ध कक्षकों की अपेक्षा अधिक सक्षम होते हैं।
- संकर कक्षक स्थायी व्यवस्था पाने के लिए त्रिविम में विशिष्ट दिशाओं में निर्देशित होते हैं। इसलिए संकरण का प्रकार अणु की ज्यामिति दर्शाता है।
संकरण की मुख्य परिस्थितियाँ
(i) परमाणु के संयोजकता कक्ष के कक्षक संकरित होते हैं।
(ii) संकरित होने वाले कक्षकों की ऊर्जा लगभग समान होनी चाहिए।
(iii) संकरण के लिए इलेक्ट्रॉन का उत्तेजन आवश्यक नहीं है।
(iv) यह आवश्यक नहीं है कि केवल अर्ध-भृत कक्षक ही संकरण में भाग लें। कभी-कभी संयोजकता कक्ष के पूर्ण-भृत तथा खाली कक्षक भी संकरित हो सकते हैं।
4.6.1 संकरण के प्रकार
(I)
sp संकरण वाले अणुओं के उदाहरण
(II) 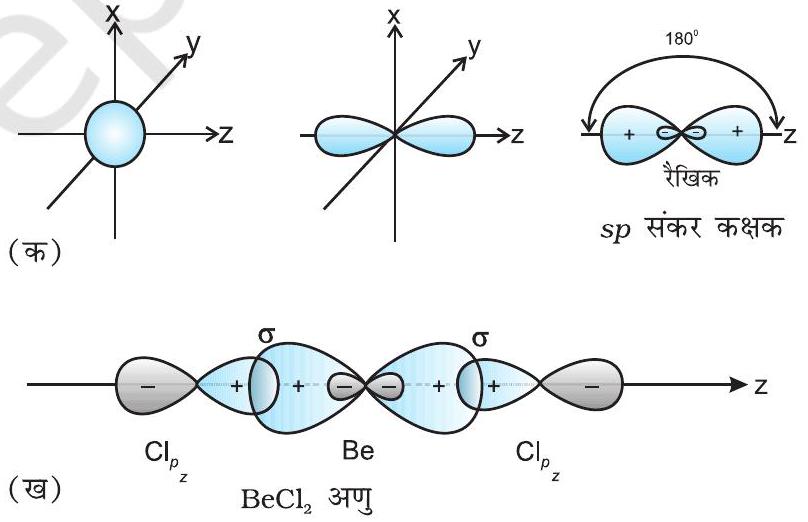
चित्र 4.10 (क)
(ख)
तथा दो
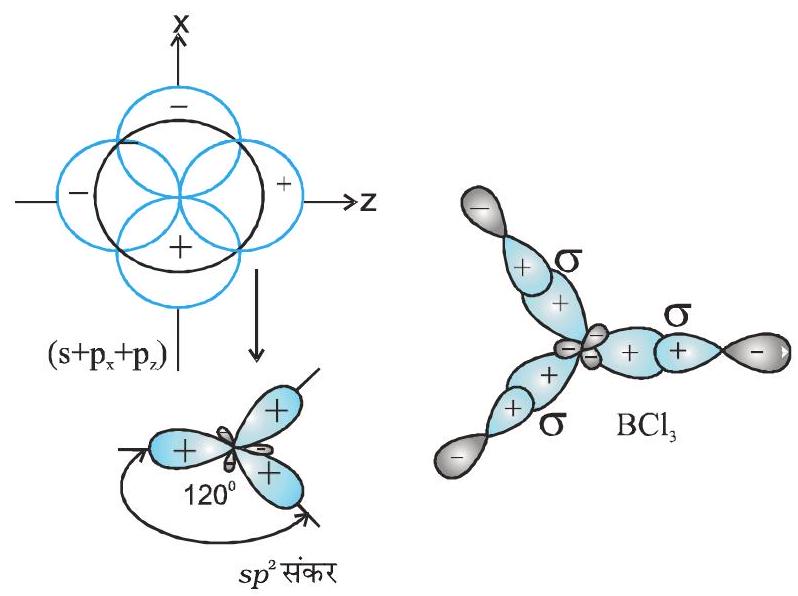
चित्र
(III)
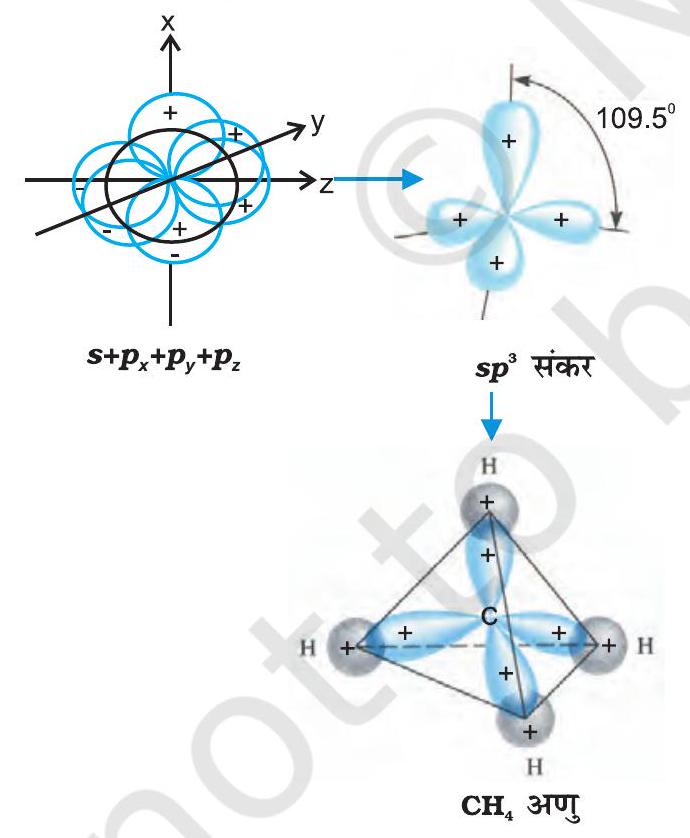
चित्र 4.12 कार्बन के
जल के अणु में ऑक्सीजन परमाणु के चार संयोजकता कक्ष, कक्षक (एक
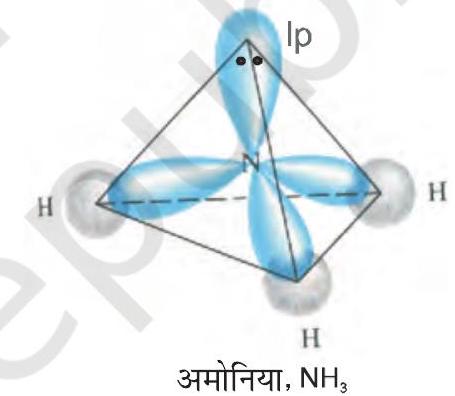
चित्र
एक-एक युग्म होता है। ये चार

चित्र
4.6.2
इस प्रकार एथीन अणु में
एथीन अणु में सिग्मा


(ख)

(ग)

(घ)

(ड़)
चित्र 4.15 एथीन में सिग्मा तथा

(a)

(b)

चित्र 4.16 एथाइन में सिग्मा तथा पाई-आबंधों का बनना
एक कार्बन परमाणु का
4.6.3
तृतीय आवर्त तत्त्वों में
(i)
| अणु/आयन की आकृति | संकरण का प्रकार | परमाण्विक कक्षक | उदाहरण |
|---|---|---|---|
| वर्ग-समतली | |||
| त्रिकोणिय द्विपिरामिडी | |||
| वर्ग पिरामिडि |
में प्रोन्नत हो जाता है। इस प्रकार फॉस्फोरस की उत्तेजित अवस्था के विन्यास को इस प्रकार दर्शाया जा सकता है-



पाँच क्लोरीन परमाणुओं द्वारा प्रदत्त इलेक्ट्रॉन युग्मों द्वारा भरे गए
इस प्रकार पाँच कक्षक (एक
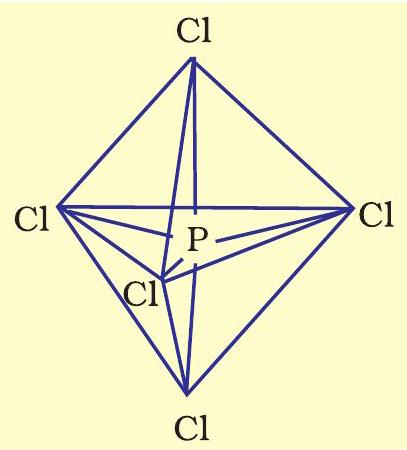
चित्र
यहाँ यह ध्यान देने योग्य बात है कि त्रिकोणीय द्विपिरामिडी ज्यामिति में सभी आबंध कोण बराबर नहीं होते हैं।
(ii)


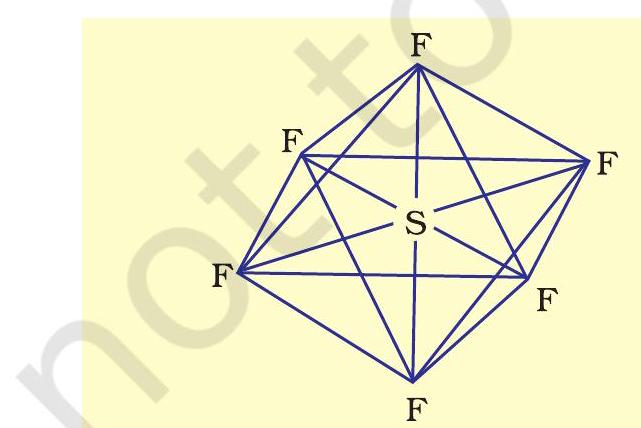
चित्र
4.7 आण्विक कक्षक सिद्धांत
आण्विक कक्षक सिद्धांत एफ. हुंड तथा आर. एस. मुलिकन द्वारा सन् 1932 में विकसित किया गया। इस सिद्धांत के मुख्य लक्षण निम्नलिखित हैं-
(i) जिस प्रकार परमाणु में इलेक्ट्रॉन विभिन्न परमाणु कक्षकों में उपस्थित रहते हैं, उसी प्रकार अणु में इलेक्ट्रॉन विभिन्न आण्विक कक्षकों में उपस्थित रहते हैं।
(ii) आण्विक कक्षक तुल्य ऊर्जाओं एवं उपयुक्त सममिति परमाणु कक्षकों के संयोग से बनते हैं।
(iii) परमाणु कक्षक में कोई इलेक्ट्रॉन केवल एक ही नाभिक के प्रभाव में रहता है, जबकि आण्विक कक्षक में उपस्थित इलेक्ट्रॉन दो या दो से अधिक नाभिकों द्वारा प्रभावित होता है। यह संख्या अणु में परमाणुओं की संख्या पर निर्भर करती है। इस प्रकार परमाणु कक्षक एकलकेंद्रीय होता है, जबकि आण्विक कक्षक बहुकेंद्रीय होता है।
(iv) बने हुए आण्विक कक्षकों की संख्या संयोग करने वाले परमाणु कक्षकों की संख्या के बराबर होती है। जब दो परमाणु कक्षकों को मिलाया जाता है, तो दो आण्विक कक्षक प्राप्त होते हैं। इनमें से एक ‘आबंधन आण्विक कक्षक’ और दूसरा प्रतिआबंधन आण्विक कक्षक कहाजाता है।
(v) आबंधन आण्विक कक्षक की ऊर्जा कम होती है। अत: उसका स्थायित्व संगत प्रतिआबंधन आण्विक कक्षक से अधिक होता है।
(vi) जिस प्रकार किसी परमाणु के नाभिक के चारों ओर इलेक्ट्रॉन प्रायिकता वितरण परमाणु कक्षक द्वारा दिया जाता है, उसी प्रकार किसी अणु में नाभिकों के समूह के चारों ओर इलेक्ट्रॉन प्रायिकता वितरण आण्विक कक्षक द्वारा दिया जाता है।
(vii) परमाणु कक्षकों की भाँति आण्विक कक्षकों को भी पाउली सिद्धांत तथा हुंड के नियम का पालन करते हुए ऑफबाऊ नियम के अनुसार भरा जाता है।
4.7.1 आण्विक कक्षकों का निर्माण : परमाणु-कक्षकों का रैखिक संयोग
जैसा आप जानते हैं, तरंग यांत्रिकी के अनुसार परमाणु कक्षक को एक तरंग फलन
कक्षक, जो अणुओं के लिए एक इलेक्ट्रॉन तरंग फलन है, को श्रोडिंगर समीकरण के हल से सीधे प्राप्त करना कठिन है। इस कठिनाई का निराकरण एक सन्निकट (Approximation) विधि के सहारे किया जाता है। इस विधि को ‘परमाणु कक्षकों का रैखिक संयोग’ (Linear Combination of Atomic Orbitals, LCAO) कहते हैं।
आइए, हम एक समनाभिकीय द्वि-परमाणुक अणु,
इस प्रकार दो आण्विक कक्षक
परमाणु कक्षकों के योग से बनने वाले आण्विक कक्षक
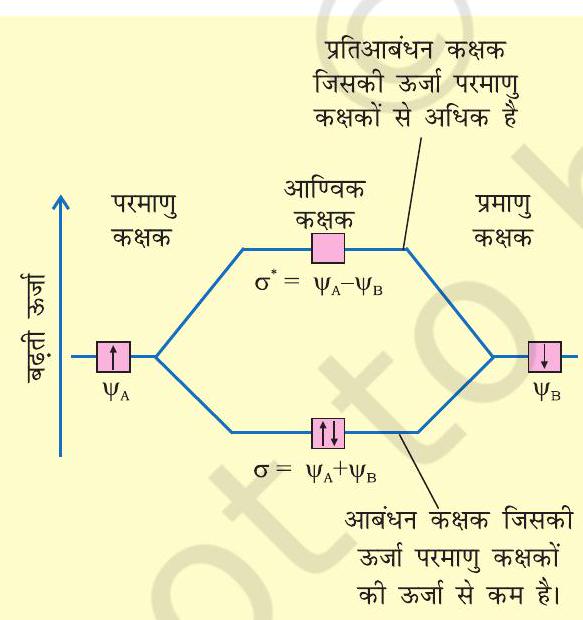
चित्र 4.19 दो परमाणु क्रमशः
यहाँ ध्यान देने योग्य बात यह है कि प्रतिआबंधन कक्षक की ऊर्जा संयोग करने वाले परमाणु कक्षकों की ऊर्जा से उतनी मात्रा में अधिक हो जाती है, जितनी मात्रा में आबंधन आण्विक कक्षक की ऊर्जा कम होती है। इस प्रकार दोनों आण्विक कक्षकों की कुल ऊर्जा वही रहती है, जो दो मूल परमाणु-कक्षकों की होती है।
4.7.2 परमाणु कक्षकों के संयोग की शर्तें
परमाणु कक्षकों के रैखिक संयोग से आण्विक कक्षकों के निर्माण के लिए निम्नलिखित शर्तें अनिवार्य हैं-
1. संयोग करने वाले परमाणु कक्षकों की ऊर्जा समान या
लगभग समान होनी चाहिए। इसका तात्पर्य यह है कि एक 
(ख)

( ग)

चित्र 4.20 (क)
ऊर्जा से कहीं अधिक होती है। यह सत्य नहीं है यदि परमाणु
- संयोग करने वाले परमाणु कक्षकों की आण्विक अक्ष तभी संयोग करेंगे, जब उनकी सममिति समान है, अन्यथा: के परितः समान सममिति होनी चाहिए। परिपाटी के अनुसार नहीं। उदाहरणार्थ-
कक्षक से संयोग करेगा, परंतु
- संयोग करने वाले परमाणु कक्षकों को अधिकतम अतिव्यापन करना चाहिए। जितना अधिक अतिव्यापन होगा, आण्विक कक्षकों के नाभिकों के बीच इलेक्ट्रॉन घनत्व उतना ही अधिक होगा।
4.7.3 आण्विक कक्षकों के प्रकार
द्वि-परमाणुक अणुओं के आण्विक कक्षकों को
[(चित्र 4.20(अ))]। यदि अंतरनाभिकीय अक्ष को
4.7.4 आण्विक कक्षकों का ऊर्जा-स्तर आरेख
हमने देखा कि दो परमाणुओं पर उपस्थित
प्रतिआबंधी आण्विक कक्षक
द्वितीय आवर्त के शेष अणुओं (जैसे-
आणिवक कक्षकों की ऊर्जा के क्रमों में महत्त्वपूर्ण अंतर यह है कि
4.7.5 इलेक्ट्रॉनी विन्यास तथा आणिवक व्यवहार
विभिन्न आण्विक कक्षकों में इलेक्ट्रॉनों का वितरण ‘इलेक्ट्रॉनिक विन्यास’ कहलाता है। इलेक्ट्रॉनों को कक्षकों की ऊर्जा के बढ़ते हुए क्रम में भरा जाता है।अणु के इलेक्ट्रॉनिक विन्यास से अणु के बारे में महत्त्वपूर्ण सूचना प्राप्त हो सकती है, जैसा आगे विवेचित है। अणुओं का स्थायित्व : यदि आबंधी आण्विक कक्षकों में उपस्थित इलेक्ट्रॉनों की संख्या
(i) अणु स्थायी होगा, यदि
(ii) अणु अस्थायी होगा, यदि
(i) में आबंधन इलेक्ट्रॉनों की संख्या अधिक होने के कारण आबंधी प्रभाव प्रबलतम होता है, जिससे एक स्थायी अणु प्राप्त होता है। दूसरी ओर (ii) में प्रति-आबंधन प्रभाव प्रबल होता है, जिसके परिणामस्वरूप अणु अस्थायी होता है।
आबंध कोटि (Bond Order) :
आबंध कोटि को आबंधी आण्विक कक्षकों एवं प्रतिआबंधी आण्विक कक्षकों में उपस्थित इलेक्ट्रॉनों की संख्या के अंतर के आधे के रूप में परिभाषित किया जाता है-
आबंध कोटि किसी अणु में उपस्थित सहसंयोजी आबंधों की संख्या बताती है। यदि
आबंध की प्रकृति
जैसा बताया गया है, आबंध-कोटि किसी अणु में उपस्थित सहसंयोजी आबंधों की संख्या बताती है। उदाहरणार्थ- यदि आबंध कोटि 1,2 या 3 हो, तो उसमें क्रमशः एकल, द्वि अथवा त्रि आबंध होंगे।
आबंध-लंबाई
सामान्यतः किसी अणु में दो परमाणुओं के बीच आबंध कोटि आबंध लंबाई का एक सन्निकट माप होता हैं। आबंध लंबाई आबंध-कोटि के व्युत्क्रमानुपी होती है। जैसे-जैसे आबंध कोटि बढ़ती है, वैसे-वैसे आबंध लंबाई घटती जाती है।
चुंबकीय स्वभाव
यदि किसी अणु के सभी आण्विक कक्षक द्वि-पूरित युग्मित हों, तो पदार्थ प्रतिचुंबकीय (Diamagnetic) होता है। ऐसे अणु चुंबकीय क्षेत्र में प्रतिकर्षित होते हैं, परंतु यदि किसी अणु के एक या अधिक आण्विक कक्षकों में अयुग्मित इलेक्ट्रॉन हों, तो वह अणु अनुचुंबकीय (Paramagnetic) होता है। ऐसे अणु चुंबकीय क्षेत्र में आकर्षित होते हैं।
4.8 समनाभिकीय द्विपरमाणुक अणुओं में आबंधन
इस खंड में हम कुछ समनाभिकीय अणुओं में आबंधन की चर्चा करेंगे।
- हाइड्रोजन अणु
हाइड्रोजन अणु की आबंध कोटि को इस प्रकार परिकलित किया जा सकता है।
आबंध कोटि
इसका अर्थ यह है कि हाइड्रोजन अणु में हाइड्रोजन के दो परमाणु एक-दूसरे से एकल सहसंयोजी आबंध द्वारा आबंधित होते हैं। हाइड्रोजन अणु की वियोजन ऊर्जा
ये इलेक्ट्रॉन
चूँकि
- लीथियम अणु
इस विन्यास को
- कार्बन अणु
अथवा
- ऑक्सीजन अणु
अथवा
इसलिए
इसी प्रकार आवर्त सारणी के द्वितीय आवर्त के अन्य समनाभिकीय द्विपरमाणुक अणुओं के इलेक्ट्रॉनिक विन्यास लिखे जाकते हैं।
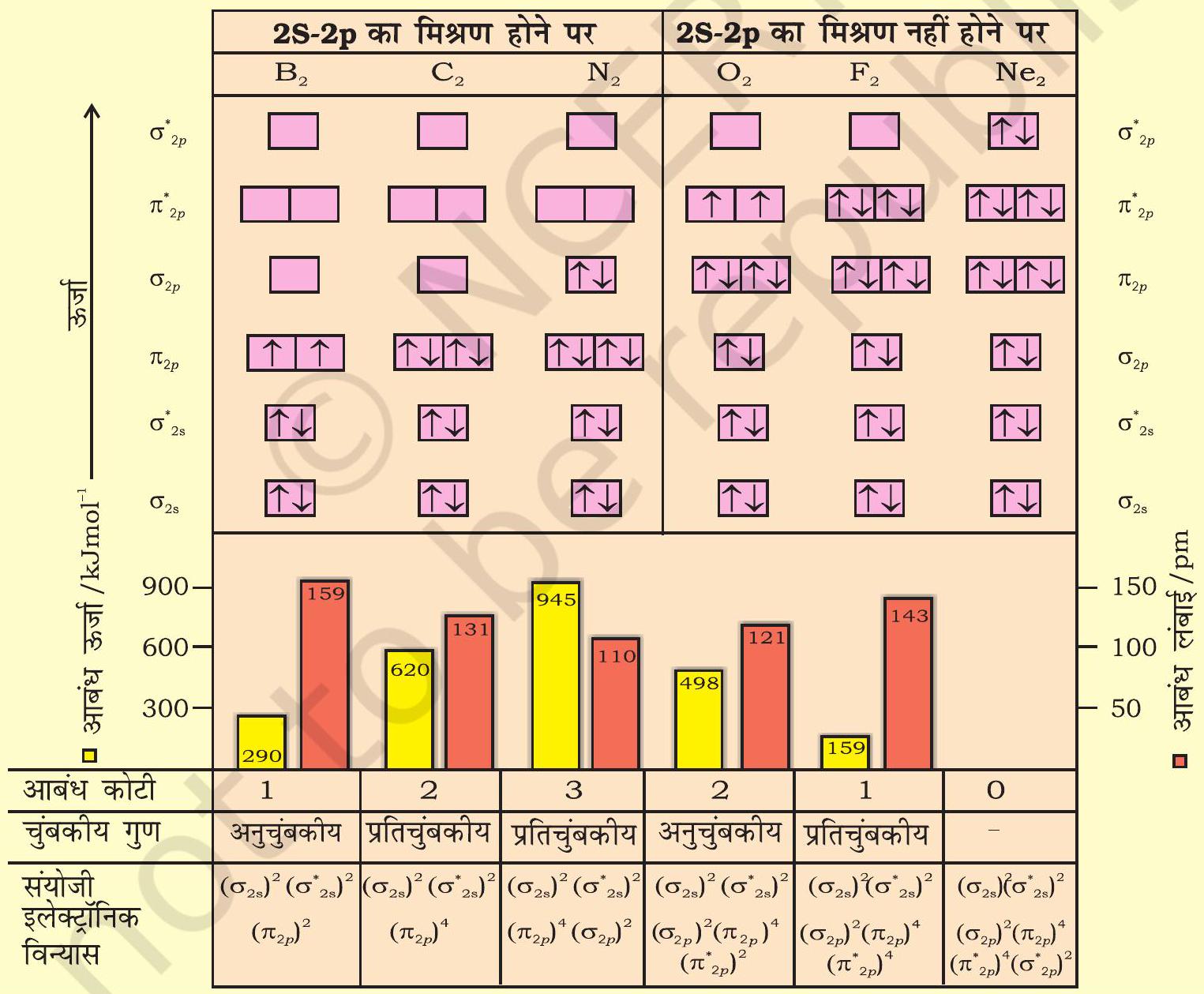
चित्र
आण्विक कक्षकों का क्रम तथा उनमें इलेक्ट्रॉनों की संख्या दर्शाई गई है। आबंध-ऊर्जा, आबंध-कोटि, चुंबकीय गुण तथा संयोजी इलेक्ट्रॉन विन्यास कक्षक आरेखों के नीचे प्रदार्शित हैं।
4.9 हाइड्रोजन आबंधन
नाइट्रोजन, ऑक्सीजन तथा फ्लुओरीन-ये तीन अत्यधिक विद्युत् ॠणात्मक तत्त्व जब परमाणु सहसंयोजक आबंध द्वारा हाइड्रोजन परमाणु से जुड़े होते हैं, तब सहसंयोजी आबंध के इलेक्ट्रॉन अधिक विद्युत् ॠणात्मक तत्त्व की ओर स्थानांतरित हो जाते हैं। फलस्वरूप प्राप्त आंशिक धनावेशित हाइड्रोजन परमाणु किसी दूसरे विद्युत् ऋणात्मक परमाणु के साथ एक नया आबंध बनाता है। इस आबंध को ‘हाइड्रोजन आबंध’ कहते हैं। यह आबंध सहसंयोजी आबंध से दुर्वल होता है। उदाहरणार्थ-
यहाँ पर हाइड्रोजन आबंध दो परमाणुओं के बीच एक सेतु का कार्य करता है, जो एक परमाणु को सहसंयोजक आबंध तथा दूसरे को हाइड्रोजन आबंध द्वारा जोड़कर रखता है। हाइड्रोजन आबंध को डॉटेड रेखा (……) द्वारा दर्शाते हैं, जबकि सहसंयोजन आबंध को ठोस रेखा (-) द्वारा दर्शाते हैं। इस प्रकार हाइड्रोजन आबंध को उस आकर्षण बल के रूप में परिभाषित किया जा सकता है, जो एक अणु के हाइड्रोजन परमाणु को दूसरे अणु के विद्युत् ॠणात्मक परमाणु
4.9.1 हाइड्रोजन आबंध बनने का कारण
जब हाइड्रोजन परमाणु किसी प्रबल विद्युत् ऋणात्मक तत्त्व ’
हाइड्रोजन आबंध का परिमाण यौगिक की भौतिक अवस्था पर निर्भर करता है। ठोस अवस्था में यह अधिकतम होता है तथा गैसीय अवस्था में न्यूनतम। इस तरह से हाइड्रोजन आबंध यौगिकों की संरचना तथा गुणधर्मों को प्रबलता से प्रभावित करते हैं।
4.9.2 हाइड्रोजन आबंधों के प्रकार
हाइड्रोजन आबंध दो प्रकार के होते हैं-(i) अंतर-अणुक हाइड्रोजन आबंध
(ii) अंतरा-अणुक हाइड्रोजन आबंध
(i) अंतर-अणुक हाइड्रोजन आबंध- ये आबंध समान अथवा विभिन्न यौगिकों के दो अलग-अलग अणुओं के बीच बनते हैं। उदाहरणार्थ-
(ii) अंतरा-अणुक हाइड्रोजन आबंध- ये आबंध एक ही अणु में उपस्थित हाइड्रोजन परमाणु तथा अधिक विद्युत् ॠणात्मक परमाणु (
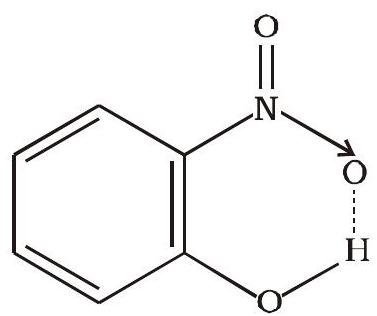
चित्र
सारांश
इलेक्ट्रो धनायनों तथा इलेक्ट्रो ऋणायनों के विरचन की क्रियाविधि को सर्वप्रथम कॉसेल ने संबंधित आयन द्वारा उत्कृष्ट गैस विन्यास की प्राप्ति के साथ संबंधित किया। आयनों के बीच वैद्युत आकर्षण के कारण स्थायित्व उत्पन्न होता है, जो वैद्युत संयोजकता का आधार है।
लूइस ने सर्वप्रथम सहसंयोजी आबंधन की व्याख्या परमाणुओं द्वारा इलेक्ट्रॉन युग्म के सहभाजन के रूप में की। इस प्रक्रिया द्वारा संबंधित परमाणु उत्कृष्ट गैस विन्यास प्राप्त करते हैं। लूइस बिंदु चिह्न किसी तत्त्व के परमाणु के संयोजकता इलेक्ट्रॉनों को दर्शाते हैं तथा लूइस बिंदु संरचनाएँ अणुओं में आबंधन का चित्रण करती हैं।
आयनिक यौगिक धनायनों तथा ऋणायनों की निश्चित क्रम में त्रिविमीय व्यवस्था होती है, जिसे ‘क्रिस्टल जालक’ कहा जाता है। क्रिस्टलीय गैसों में धनायन एवं ऋणायन के मध्य आवेश संतुलित होता है। क्रिस्टल जालक का जालक विरचन एंथैल्पी द्वारा स्थिरीकरण होता है।
दो परमाणुओं के बीच एकल सहसंयोजी आबंध का विरचन एक-एक इलेक्ट्रॉन युग्म के सहभाजन द्वारा होता है, जबकि दो या तीन इलेक्ट्रॉन युग्मों के सहभाजन के फलस्वरूप बहु आबंध निर्मित होते हैं। कुछ आबंधी परमाणुओं पर ऐसे इलेक्ट्रॉन युग्म उपस्थित होते हैं, जो आबंधन में भाग नहीं लेते। ये ‘इलेक्ट्रॉनों के एकाकी युग्म’ कहलाते हैं। लूइस बिंदु संरचना अणु में प्रत्येक परमाणु पर आबंधी युग्मों तथा एकाकी युग्मों को दर्शाती है। रासायनिक आबंधों के कुछ प्रमुख प्राचल, जैसे-आबंध एंथैल्पी, आबंध कोटि विद्युत् ऋणात्मक्ता तथा आबंध ध्रुवणता यौगिकों के गुणों को प्रभावित करते हैं।
बहुत से अणुओं तथा बहुपरमाणुक आयनों को मात्र एक लूइस संरचना द्वारा प्रदर्शित नहीं किया जा सकता है। ऐसी स्पीशीज़ के लिए अनेक संरचनाएँ लिखी जाती हैं, जिनके ढाँचे की संरचना समान होती है। ये सभी संरचनाएँ सम्मिलित रूप में अणु या आयन की वास्तविक संरचना प्रदर्शित करती हैं। यह एक महत्त्वपूर्ण तथा अति उपयोगी अवधारणा है, जिसे ‘अनुनाद’ कहा जाता है। योगदान देने वाली विहित संरचनाओं का अनुनाद संकर अणु या आयन की वास्तविक संरचना प्रदर्शित करता है।
वी. एस. ई. पी. आर. मॉडल का उपयोग अणुओं की ज्यामितीय आकृतियों के पूर्वानुमान के लिए किया जाता है। यह मॉडल इस कल्पना पर आधारित है कि अणु में इलेक्ट्रॉन युग्म एक-दूसरे को प्रतिकर्षित करते हैं। इस मॉडल के अनुसार, आण्विक ज्यामिति एकाकी युग्म-एकाकी युग्म, एकाकी युग्म-आबंधी युग्म तथा आबंधी युग्म-आबंधी युग्म प्रतिकर्षणों पर निर्भर करती हैं। इन प्रतिकर्षण बलों का क्रम इस प्रकार है-
सहसंयोजी आबंधन का सहसंयोजकता आबंध सिद्धांत सहसंयोजी आबंध बनने के ऊर्जा-विज्ञान पर आधारित है, जिसपर लूइस तथा वी. एस. ई. पी. आर. मॉडल प्रकाश नहीं डालते। मूलतः VB सिद्धांत कक्षकों के अतिव्यापन पर आधारित है। उदाहरणस्वरूप
बहुपरमाणुक अणुओं की विशिष्ट आकृतियों को स्पष्ट करने के लिए पॉलिंग ने परमाणु कक्षकों के संकरण की अवधारणा को प्रस्तुत किया।
आण्विक कक्षक सिद्धांत परमाणु कक्षकों के संयोग एवं व्यवस्था से संपूर्ण अणु से संबद्ध आण्विक कक्षकों के बनने के रूप में आबंधन का वर्णन करता है। आण्विक कक्षकों की संख्या संयोग करनेवाले परमाणु कक्षकों की संख्या के बराबर
होती है। आबंधी आण्विक कक्षक नाभिकों के मध्य इलेक्ट्रॉन घनत्व बढ़ा देते हैं तथा इनकी ऊर्जा व्यक्तिगत परमाणु कक्षकों की ऊर्जा से कम होती है। प्रतिआबंधी आण्विक कक्षक में नाभिकों के मध्य शून्य इलेक्ट्रॉन घनत्व होता है। इन कक्षकों की ऊर्जा व्याक्तिगत परमाणु कक्षकों की अपेक्षा उच्च होती है।
अणुओं का इलेक्ट्रॉन विन्यास आण्विक कक्षकों में इलेक्ट्रॉनों को ऊर्जा के बढ़ते क्रम में भरते हुए लिखा जाता है। परमाणुओं की तरह यहाँ भी पॉउली अपवर्जन नियम तथा हुंड के नियम लागू होते हैं। यदि अणु के आबंधी आण्विक कक्षकों में इलेक्ट्रॉनों की संख्या प्रति-आबंधी आण्विक कक्षकों में उपस्थित इलेक्ट्रॉनों की संख्या से अधिक होती है, तो अणु स्थायी होता है।
जब एक हाइड्रोजन परमाणु दो अत्यंत विद्युत् ऋणात्मक परमाणुओं










