The moving power of mathematical invention is not reasoning but imagination. - A.DEMORGAN

11.1 भूमिका (Introduction)

कक्षा XI में, वैश्लेषिक ज्यामिति का अध्ययन करते समय द्वि-विमीय और त्रि-विमीय विषयों के परिचय में हमने स्वयं को केवल कार्तीय विधि तक सीमित रखा है। इस पुस्तक के पिछले अध्याय में हमने सदिशों की मूल संकल्पनाओं का अध्ययन किया है। अब हम सदिशों के बीजगणित का त्रि-विमीय ज्यामिति में उपयोग करेंगे। त्रि-विमीय ज्यामिति में इस उपागम का उद्देश्य है कि यह इसके अध्ययन को अत्यंत सरल एवं सुरुचिपूर्ण (सुग्राहय) बना देता है।*

इस अध्याय में हम दो बिंदुओं को मिलाने वाली रेखा के दिक्-कोज्या व दिक्-अनुपात का अध्ययन करेंगे और विभिन्न स्थितियों में अंतरिक्ष में रेखाओं और तलों के समीकरणों, दो रेखाओं, दो तलों व एक रेखा और एक तल के बीच का कोण, दो विषमतलीय रेखाओं के बीच न्यूनतम दूरी व एक तल की एक बिंदु से दूरी के विषय में भी विचार विमर्श करेंगे। उपरोक्त परिणामों में से अधिकांश परिणामों को सदिशों के रूप में प्राप्त करते हैं। तथापि हम इनका कार्तीय रूप में भी अनुवाद करेंगे जो कालांतर में स्थिति का स्पष्ट ज्यामितीय और विश्लेषणात्मक चित्रण प्रस्तुत कर सकेगा।

Leonhard Euler $(\mathbf{1 7 0 7 - 1 7 8 3 })$

11.2 रेखा के दिक्-कोसाइन और दिक्-अनुपात (Direction Cosines and Direction Ratios of a Line)

अध्याय 10 में, स्मरण कीजिए, कि मूल बिंदु से गुजरने वाली सदिश रेखा $\mathrm{L}$ द्वारा $x, y$ और $z$-अक्षों के साथ क्रमश $\alpha, \beta$ और $\gamma$ बनाए गए कोण दिक्-कोण कहलाते हैं तब इन कोणों की कोसाइन नामतः $\cos \alpha, \cos \beta$ और $\cos \gamma$ रेखा $\mathrm{L}$ के दिक्-कोसाइन (direction cosines or dc’s)कहलाती हैं।

यदि हम $\mathrm{L}$ की दिशा विपरीत कर देते हैं तो दिक्-कोण, अपने संपूरकों में अर्थात् $\pi-\alpha, \pi-\beta$ और $\pi$ - $\gamma$ से बदल जाते हैं। इस प्रकार, दिक्-कोसाइन के चिह्न बदल जाते हैं।

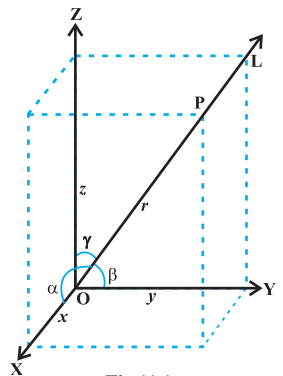
आकृति 11.1

ध्यान दीजिए, अंतरिक्ष में दी गई रेखा को दो विपरीत दिशाओं में बढ़ा सकते हैं और इसलिए इसके दिक्-कोसाइन के दो समूह हैं। इसलिए अंतरिक्ष में ज्ञात रेखा के लिए दिक्-कोसाइन के अद्वितीय समूह के लिए, हमें ज्ञात रेखा को एक सदिश रेखा लेना चाहिए। इन अद्वितीय दिक्-कोसाइन को $l, m$ और $n$ के द्वारा निर्दिष्ट किए जाते हैं।

टिप्पणी अंतरिक्ष में दी गई रेखा यदि मूल बिंदु से नहीं गुजरती है तो इसकी दिक्-कोसाइन को ज्ञात करने के लिए, हम मूल बिंदु से दी गई रेखा के समांतर एक रेखा खींचते हैं। अब मूल बिंदु से इनमें से एक सदिश रेखा के दिक्-अनुपात ज्ञात करते हैं क्योंकि दो समांतर रेखाओं के दिक्-अनुपातों के समूह समान (वही) होते हैं।

एक रेखा के दिक्-कोसाइन के समानुपाती संख्याओं को रेखा के दिक्-अनुपात (direction ratios or $\left.d r^{\prime} s\right)$ कहते हैं। यदि एक रेखा के दिक्-कोसाइन $l, m, n$ व दिक्-अनुपात $a, b, c$ हों तब किसी शून्येतर $\lambda \in \mathbf{R}$ के लिए $a=\lambda l, b=\lambda m$ और $c=\lambda n$

टिप्पणी कुछ लेखक दिक्-अनुपातों को दिक्-संख्याएँ भी कहते हैं।

मान लीजिए एक रेखा के दिक्-अनुपात $a, b, c$ और रेखा की दिक्-कोसाइन $l, m, n$ है। तब

$$ \frac{l}{a}=\frac{m}{b}=\frac{n}{c}=k \text { (मान लीजिए), } k \text { एक अचर है। } $$

इसलिए $\qquad l=a k, m=b k, n=c k$

परंतु $\qquad l^{2}+m^{2}+n^{2}=1$

इसलिए $ \qquad k^{2}\left(a^{2}+b^{2}+c^{2}\right)=1 $

या $ \qquad k= \pm \frac{1}{\sqrt{a^{2}+b^{2}+c^{2}}} $

अतः (1) से, रेखा की दिक्-कोसाइन (d.c.’s) $ \qquad l= \pm \frac{a}{\sqrt{a^{2}+b^{2}+c^{2}}}, m= \pm \frac{b}{\sqrt{a^{2}+b^{2}+c^{2}}}, n= \pm \frac{c}{\sqrt{a^{2}+b^{2}+c^{2}}} $

किसी रेखा के लिए यदि रेखा के दिक्-अनुपात क्रमश: $a, b, c$ है, तो $k a, k b, k c ; k \neq 0$ भी दिक्-अनुपातों का एक समूह है। इसलिए एक रेखा के दिक्-अनुपातों के दो समूह भी समानुपाती होंगे। अतः किसी एक रेखा के दिक्-अनुपातों के असंख्य समूह होते हैं।

11.2.1 दो बिंदुओं को मिलाने वाली रेखा की दिक्-कोसाइन (Direction cosines of a line passing through two points)

क्योंकि दो दिए बिंदुओं से होकर जाने वाली रेखा अद्वितीय होती है। इसलिए दो दिए गए बिंदुओं $\mathrm{P}\left(x _{1}, y _{1}, z _{1}\right)$ और $\mathrm{Q}\left(x _{2}, y _{2}, z _{2}\right)$ से गुजरने वाली रेखा की दिक्-कोसाइन को निम्न प्रकार से ज्ञात कर सकते हैं (आकृति 11.3 (a)।

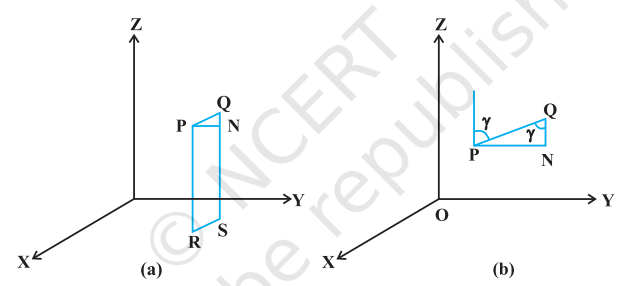
आकृति 11.2

मान लीजिए कि रेखा $\mathrm{PQ}$ की दिक्-कोसाइन $l, m, n$ हैं और यह $x, y$ और $z$-अक्ष के साथ कोण क्रमश: $\alpha, \beta, \gamma$ बनाती हैं।

मान लीजिए $\mathrm{P}$ और $\mathrm{Q}$ से लंब खींचिए जो $\mathrm{XY}$-तल को $\mathrm{R}$ तथा $\mathrm{S}$ पर मिलते हैं। $\mathrm{P}$ से एक अन्य लंब खींचिए जो $\mathrm{QS}$ को $\mathrm{N}$ पर मिलता है। अब समकोण त्रिभुज $\mathrm{PNQ}$ में, $\angle \mathrm{PQN}=\gamma$ (आकृति 11.2 (b)) इसलिए

$$ \begin{aligned} & \cos \gamma=\frac{\mathrm{NQ}}{\mathrm{PQ}}=\frac{z _{2}-z _{1}}{\mathrm{PQ}} \\ & \cos \alpha=\frac{x _{2}-x _{1}}{\mathrm{PQ}} \text { और } \cos \beta=\frac{y _{2}-y _{1}}{\mathrm{PQ}} \end{aligned} $$

इसी प्रकार अतः बिंदुओं $\mathrm{P}\left(x _{1}, y _{1}, z _{1}\right)$ तथा $\mathrm{Q}\left(x _{2}, y _{2}, z _{2}\right)$ को जोड़ने वाले रेखाखंड PQ कि दिक्-कोसाइन

$$ \frac{x _{2}-x _{1}}{\mathrm{PQ}}, \frac{y _{2}-y _{1}}{\mathrm{PQ}}, \frac{z _{2}-z _{1}}{\mathrm{PQ}} \text { हैं। } $$

जहाँ $ \qquad \mathrm{PQ}=\sqrt{\left(x _{2}-x _{1}\right)^{2}+\left(y _{2}-y _{1}\right)^{2}+\left(z _{2}-z _{1}\right)^{2}} $

टिप्पणी बिंदुओं $\mathrm{P}\left(x _{1}, y _{1}, z _{1}\right)$ तथा $\mathrm{Q}\left(x _{2}, y _{2}, z _{2}\right)$ को जोड़ने वाले रेखाखंड के दिक्-अनुपात निम्न प्रकार से लिए जा सकते हैं।

$$ x _{2}-x _{1}, y _{2}-y _{1}, z _{2}-z _{1}, \text { या } x _{1}-x _{2}, y _{1}-y _{2}, z _{1}-z _{2} $$

उदाहरण 1 यदि एक रेखा $x, y$ तथा $z$-अक्षों की धनात्मक दिशा के साथ क्रमशः $90^{\circ}, 60^{\circ}$ तथा $30^{\circ}$ का कोण बनाती है तो दिक्-कोसाइन ज्ञात कीजिए।

हल मान लीजिए रेखा की दिक्-कोसाइन $l, m, n$ है। तब $l=\cos 90^{\circ}=0, m=\cos 60^{\circ}=\frac{1}{2}$, $n=\cos 30^{\circ}=\frac{\sqrt{3}}{2}$

उदाहरण 2 यदि एक रेखा के दिक्-अनुपात $2,-1,-2$ हैं तो इसकी दिक्-कोसाइन ज्ञात कीजिए।

हल दिक्-कोसाइन निम्नवत् हैं

$$ \frac{2}{\sqrt{2^{2}+(-1)^{2}+(-2)^{2}}}, \frac{-1}{\sqrt{2^{2}+(-1)^{2}+(-2)^{2}}}, \frac{-2}{\sqrt{2^{2}+(-1)^{2}+(-2)^{2}}} $$

अर्थात् $ \qquad \frac{2}{3}, \frac{-1}{3}, \frac{-2}{3} $

उदाहरण 3 दो बिंदुओं $(-2,4,-5)$ और $(1,2,3)$ को मिलाने वाली रेखा की दिक्-कोसाइन ज्ञात कीजिए।

हल हम जानते हैं कि दो बिंदुओं $\mathrm{P}\left(x _{1}, y _{1}, z _{1}\right)$ और $\mathrm{Q}\left(x _{2}, y _{2}, z _{2}\right)$ को मिलाने वाली रेखा की दिक्-कोसाइन

हैं, जहाँ $ \qquad \frac{x _{2}-x _{1}}{\mathrm{PQ}}, \frac{y _{2}-y _{1}}{\mathrm{PQ}}, \frac{z _{2}-z _{1}}{\mathrm{PQ}} $

$$ \mathrm{PQ}=\sqrt{\left(x _{2}-x _{1}\right)^{2}+\left(y _{2}-y _{1}\right)^{2}+\left(z _{2}-z _{1}\right)^{2}} $$

यहाँ $\mathrm{P}$ और $\mathrm{Q}$ क्रमशः $(-2,4,-5)$ और $(1,2,3)$ हैं।

इसलिए $ \qquad P Q=\sqrt{(1-(-2))^{2}+(2-4)^{2}+(3-(-5))^{2}}=\sqrt{77} $

इसलिए दो बिंदुओं को मिलाने वाली रेखा की दिक्-कोसाइन हैं:

$ \qquad \frac{3}{\sqrt{77}}, \frac{-2}{\sqrt{77}}, \frac{8}{\sqrt{77}} $

उदाहरण 4 $ x, y$ और $z$-अक्षों की दिक्-कोसाइन ज्ञात कीजिए।

हल $x$-अक्ष क्रमशः $x, y$ और $z$-अक्ष के साथ $0^{\circ}, 90^{\circ}$ और $90^{\circ}$ के कोण बनाता है। इसलिए $x$-अक्ष की दिक्-कोसाइन $\cos 0^{\circ}, \cos 90^{\circ}, \cos 90^{\circ}$ अर्थात् $1,0,0$ हैं। इसी प्रकार $y$-अक्ष और $z$-अक्ष की दिक्-कोसाइन क्रमशः $0,1,0$ और $0,0,1$ हैं।

उदाहरण 5 दर्शाइए कि बिंदु $\mathrm{A}(2,3,-4), \mathrm{B}(1,-2,3)$ और $\mathrm{C}(3,8,-11)$ संरेख हैं।

हल $\mathrm{A}$ और $\mathrm{B}$ को मिलाने वाली रेखा के दिक्-अनुपात

$1-2,-2-3,3+4$ अर्थात् $-1,-5,7$ हैं।

$B$ और $C$ को मिलाने वाली रेखा के दिक्-अनुपात $3-1,8+2,-11-3$, अर्थात्, $2,10,-14$ हैं।

स्पष्ट है कि $\mathrm{AB}$ और $\mathrm{BC}$ के दिक्-अनुपात समानुपाती हैं। अतः $\mathrm{AB}$ और $\mathrm{BC}$ समांतर हैं, परंतु $\mathrm{AB}$ और $\mathrm{BC}$ दोनों में $\mathrm{B}$ उभयनिष्ठ है। अत: $\mathrm{A}, \mathrm{B}$, और $\mathrm{C}$ संरेख बिंदु हैं।

प्रश्नावली 11.1

1. यदि एक रेखा $x, y$ और $z$-अक्ष के साथ क्रमश: $90^{\circ}, 135^{\circ}, 45^{\circ}$ के कोण बनाती है तो इसकी दिक्-कोसाइन ज्ञात कीजिए।

2. एक रेखा की दिक्-कोसाइन ज्ञात कीजिए जो निर्देशांक्षों के साथ समान कोण बनाती है।

3. यदि एक रेखा के दिक्-अनुपात $-18,12,-4$, हैं तो इसकी दिक्-कोसाइन क्या हैं?

4. दर्शाइए कि बिंदु $(2,3,4),(-1,-2,1),(5,8,7)$ संरेख हैं।

5. एक त्रिभुज की भुजाओं की दिक्-कोसाइन ज्ञात कीजिए यदि त्रिभुज के शीर्ष बिंदु $(3,5,-4),(-1,1,2)$ और $(-5,-5,-2)$ हैं।

11.3 अंतरिक्ष में रेखा का समीकरण (Equation of a Line in Space)

कक्षा XI में द्वि-विमीय तल में रेखाओं का अध्ययन करने के पश्चात् अब हम अंतरिक्ष में एक रेखा के सदिश तथा कार्तीय समीकरणों को ज्ञात करेंगे।

एक रेखा अद्वितीयतः निर्धारित होती है, यदि

(i) यह दिए बिंदु से दी गई दिशा से होकर जाती है, या

(ii) यह दो दिए गए बिंदुओं से होकर जाती है।

11.3.1 दिए गए बिंदु $\mathrm{A}$ से जाने वाली तथा दिए गए सदिश $\vec{b}$ के समांतर रेखा का समीकरण (Equation of a line through a given point $\mathbf{A}$ and parallel to a given vector $\vec{b}$ )

समकोणिक निर्देशांक्ष निकाय के मूल बिंदु $\mathrm{O}$ के सापेक्ष मान लीजिए कि बिंदु $\mathrm{A}$ का सदिश $\vec{a}$ है। मान लीजिए कि बिंदु $\mathrm{A}$ से जाने वाली तथा दिए गए सदिश $\vec{b}$ के समांतर रेखा $l$ है। मान लीजिए कि $l$ पर स्थित किसी स्वेच्छ बिंदु $\mathrm{P}$ का स्थिति सदिश $\vec{r}$ है (आकृति 11.3)।

तब $\overrightarrow{\mathrm{AP}}$ सदिश $\vec{b}$ के समांतर है अर्थात् $\overrightarrow{\mathrm{AP}}=\lambda \vec{b}$, जहाँ $\lambda$ एक वास्तविक संख्या है।

परंतु $$ \overrightarrow{\mathrm{AP}}=\overrightarrow{\mathrm{OP}}-\overrightarrow{\mathrm{OA}} $$

अर्थात् $$ \lambda \vec{b}=\vec{r}-\vec{a} $$

आकृति 11.3 विलोमतः प्राचल $\lambda$ के प्रत्येक मान के लिए यह समीकरण रेखा के किसी बिंदु $\mathrm{P}$ की स्थिति प्रदान करता है। अतः रेखा का सदिश समीकरण है:

$$ \begin{equation*} \vec{r}=\vec{a}+\lambda \vec{b} \tag{1} \end{equation*} $$

टिप्पणी यदि $\vec{b}=a \hat{i}+b \hat{j}+c \hat{k}$ है तो रेखा के दिक्-अनुपात $a, b, c$ है और विलोमतः यदि एक रेखा के दिक्-अनुपात $a, b, c$ हों तो $\vec{b}=a \hat{i}+b \hat{j}+c \hat{k}$ रेखा के समांतर होगा। यहाँ $b$ को $|\vec{b}|$ न समझा जाए। सदिश रूप से कार्तीय रूप व्युत्पन्न करना (Derivation of Cartesian Form from Vector Form)

मान लीजिए कि दिए बिंदु $\mathrm{A}$ के निर्देशांक $\left(x _{1}, y _{1}, z _{1}\right)$ हैं और रेखा की दिक्-कोसाइन $a, b, c$ हैं मान लीजिए किसी बिंदु $\mathrm{P}$ के निर्देशांक $(x, y, z)$ हैं। तब

$$ \vec{r}=x \hat{i}+y \hat{j}+z \hat{k} ; \vec{a}=x _{1} \hat{i}+y _{1} \hat{j}+z _{1} \hat{k} $$

और $$ \vec{b}=a \hat{i}+b \hat{j}+c \hat{k} $$

इन मानों को (1) में प्रतिस्थापित करके $\hat{i}, \hat{j}$ और $\hat{k}$, के गुणांकों की तुलना करने पर हम पाते हैं कि

$$ \begin{equation*} x=x _{1}+\lambda a ;\quad y=y _{1}+\lambda b ; \quad z=z _{1}+\lambda c \tag{2} \end{equation*} $$

ये रेखा के प्राचल समीकरण हैं। (2) से प्राचल $\lambda$ का विलोपन करने पर, हम पाते हैं:

$$ \begin{equation*} \frac{x-x _{1}}{a}=\frac{y-y _{1}}{b}=\frac{z-z _{1}}{c} \tag{3} \end{equation*} $$

यह रेखा का कार्तीय समीकरण है।

टिप्पणी यदि रेखा की दिक्-कोसाइन $l, m, n$ हैं, तो रेखा का समीकरण

$$ \frac{x-x _{1}}{l}=\frac{y-y _{1}}{m}=\frac{z-z _{1}}{n} \text { हैं। } $$

उदाहरण 6 बिंदु $(5,2,-4)$ से जाने वाली तथा सदिश $3 \hat{i}+2 \hat{j}-8 \hat{k}$ के समांतर रेखा का सदिश तथा कार्तीय समीकरणों को ज्ञात कीजिए।

हल हमें ज्ञात है, कि

$$ \vec{a}=5 \hat{i}+2 \hat{j}-4 \hat{k} \text { और } \vec{b}=3 \hat{i}+2 \hat{j}-8 \hat{k} $$

इसलिए, रेखा का सदिश समीकरण है:

$$ \vec{r}=5 \hat{i}+2 \hat{j}-4 \hat{k}+\lambda(3 \hat{i}+2 \hat{j}-8 \hat{k})[(1) \text { से }] $$

चूँकि रेखा पर स्थित किसी बिंदु $\mathrm{P}(x, y, z)$ की स्थिति सदिश $\vec{r}$ है, इसलिए

$$ \begin{aligned} x \hat{i}+y \hat{j}+z \hat{k} & =5 \hat{i}+2 \hat{j}-4 \hat{k}+\lambda(3 \hat{i}+2 \hat{j}-8 \hat{k}) \\ & =(5+3 \lambda) \hat{i}+(2+2 \lambda) \hat{j}+(-4-8 \lambda) \hat{k} \end{aligned} $$

$\lambda$ का विलोपन करने पर हम पाते हैं कि

$$ \frac{x-5}{3}=\frac{y-2}{2}=\frac{z+4}{-8} $$

जो रेखा के समीकरण का कार्तीय रूप है।

11.4 दो रेखाओं के मध्य कोण (Angle between two lines)

मान लीजिए कि $\mathrm{L} _{1}$ और $\mathrm{L} _{2}$ मूल बिंदु से गुजरने वाली दो रेखाएँ हैं जिनके दिक्-अनुपात क्रमशः $a _{1}, b _{1}, c _{1}$ और $a _{2}, b _{2}, c _{2}$, है। पुन: मान लीजिएक $\mathrm{L} _{1}$ पर एक बिंदु $\mathrm{P}$ तथा $\mathrm{L} _{2}$ पर एक बिंदु $\mathrm{Q}$ है। आकृति 11.4 में दिए गए सदिश $\mathrm{OP}$ और $\mathrm{OQ}$ पर विचार कीजिए। मान लीजिए कि $\mathrm{OP}$ और $\mathrm{OQ}$ के बीच न्यून कोण $\theta$ है। अब स्मरण कीजिए कि सदिशों $\mathrm{OP}$ और $\mathrm{OQ}$ के घटक क्रमशः $a _{1}, b _{1}$, $c _{1}$ और $a _{2}, b _{2}, c _{2}$ हैं। इसलिए उनके बीच का कोण $\theta$ $\cos \theta=\left|\frac{a _{1} a _{2}+b _{1} b _{2}+c _{1} c _{2}}{\sqrt{a _{1}^{2}+b _{1}^{2}+c _{1}^{2}} \sqrt{a _{2}^{2}+b _{2}^{2}+c _{2}^{2}}}\right|$ द्वारा प्रदत्त है।

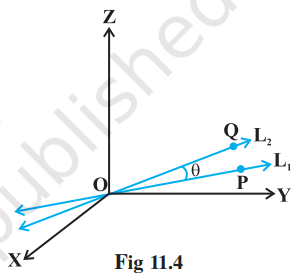
पुनः $\sin \theta$ के रूप में, रेखाओं के बीच का कोण

$$ \begin{aligned} \sin \theta & =\sqrt{1-\cos ^{2} \theta} \\ & =\sqrt{1-\frac{(a_1 a_2+b_1 b_2+c_1 c_2)^{2}}{(a_1^{2}+b_1^{2}+c_1^{2})(a_2^{2}+b_2^{2}+c_2^{2})}} \\ & =\frac{\sqrt{(a_1^{2}+b_1^{2}+c_1^{2})(a_2^{2}+b_2^{2}+c_2^{2})-(a_1 a_2+b_1 b_2+c_1 c_2)^{2}}}{\sqrt{(a_1^{2}+b_1^{2}+c_1^{2})} \sqrt{(a_2^{2}+b_2^{2}+c_2^{2})}} \\ & =\frac{\sqrt{(a_1 b_2-a_2 b_1)^{2}+(b_1 c_2-b_2 c_1)^{2}+(c_1 a_2-c_2 a_1)^{2}}}{\sqrt{a_1^{2}+b_1^{2}+c_1^{2}} \sqrt{a_2^{2}+b_2^{2}+c_2^{2}}} \end{aligned} $$

टिप्पणी उस स्थिति में जब रेखाएँ $\mathrm{L} _{1}$ और $\mathrm{L} _{2}$ मूल बिंदु से नहीं गुजरती है तो हम $\mathrm{L} _{1}$ और $\mathrm{L} _{2}$ के समांतर, मूल बिंदु से गुजरने वाली रेखाएँ क्रमशः $\mathrm{L} _{1}^{\prime}$ व $\mathrm{L} _{2}^{\prime}$ लेते हैं।

यदि रेखाओं $\mathrm{L} _{1}$ और $\mathrm{L} _{2}$ के दिक्-अनुपातों के बजाय दिक्-कोसाइन दी गई हो जैसे $\mathrm{L} _{1}$ के लिए $l _{1}, m _{1}, n _{1}$ और $\mathrm{L} _{2}$ के लिए $l _{2}, m _{2}, n _{2}$ तो (1) और (2) निम्नलिखित प्रारूप लेंगे।

$$ \begin{equation*} \cos \theta=\left|l _{1} l _{2}+m _{1} m _{2}+n _{1} n _{2}\right|\left(\text { क्योंकि } l _{1}^{2}+m _{1}^{2}+n _{1}^{2}=1=l _{2}^{2}+m _{2}^{2}+n _{2}^{2}\right) \tag{3} \end{equation*} $$

और $\quad \sin \theta=\sqrt{\left(l _{1} m _{2}-l _{2} m _{1}\right)^{2}-\left(m _{1} n _{2}-m _{2} n _{1}\right)^{2}+\left(n _{1} l _{2}-n _{2} l _{1}\right)^{2}}$

दिक्-अनुपात $a _{1}, b _{1}, c _{1}$ और $a _{2}, b _{2}, c _{2}$ वाली रेखाएँ

(i) लंबवत् है, यदि $\theta=90^{\circ}$, अर्थात्

से $$\boldsymbol{a} _{1} \boldsymbol{a} _{2}+\boldsymbol{b} _{1} \boldsymbol{b} _{2}+\boldsymbol{c} _{1} \boldsymbol{c} _{2}=\mathbf{0}$$

(ii) समांतर है, यदि $\theta=0$, अर्थात् (2)

से $$\frac{\boldsymbol{a} _{\mathbf{1}}}{\boldsymbol{a} _{2}}=\frac{\boldsymbol{b} _{\mathbf{1}}}{\boldsymbol{b} _{\mathbf{2}}}=\frac{\boldsymbol{c} _{\mathbf{1}}}{\boldsymbol{c} _{\mathbf{2}}}$$

अब हम दो रेखाओं के बीच का कोण ज्ञात करेंगे जिनके समीकरण दिए गए हैं। यदि उन रेखाओं $\vec{r}=\vec{a} _{1}+\lambda \vec{b} _{1}$ और $\vec{r}=\vec{a} _{2}+\mu \vec{b} _{2}$ के बीच न्यून कोण $\theta$ है

तब $$ \begin{equation*} \cos \theta=\left|\frac{\vec{b} _{1} \cdot \vec{b} _{2}}{\left|\vec{b} _{1}\right|\left|\vec{b} _{2}\right|}\right| \tag{1} \end{equation*} $$

कार्तीय रूप में यदि रेखाओं: $\frac{x-x _{1}}{a _{1}}=\frac{y-y _{1}}{b _{1}}=\frac{z-z _{1}}{c _{1}}$

और $$ \begin{equation*} \frac{x-x _{2}}{a _{2}}=\frac{y-y _{2}}{b _{2}}=\frac{z-z _{2}}{c _{2}} \tag{2} \end{equation*} $$

के बीच का कोण $\theta$ है जहाँ रेखाएँ (1) व (2) के दिक्-अनुपात क्रमशः $a _{1}, b _{1}, c _{1}$ तथा $a _{2,} b _{2}, c _{2}$ है तब

$$ \cos \theta=\left|\frac{a _{1} a _{2}+b _{1} b _{2}+c _{1} c _{2}}{\sqrt{a _{1}^{2}+b _{1}^{2}+c _{1}^{2}} \sqrt{a _{2}^{2}+b _{2}^{2}+c _{2}^{2}}}\right| $$

उदाहरण 7 दिए गए रेखा-युग्म के मध्य कोण ज्ञात कीजिए

$$ \vec{r}=3 \hat{i}+2 \hat{j}-4 \hat{k}+\lambda(\hat{i}+2 \hat{j}+2 \hat{k}) $$

और $$ \vec{r}=5 \hat{i}-2 \hat{j}+\mu(3 \hat{i}+2 \hat{j}+6 \hat{k}) $$

हल मान लीजिए $\vec{b} _{1}=\hat{i}+2 \hat{j}+2 \hat{k}$ और $\vec{b} _{2}=3 \hat{i}+2 \hat{j}+6 \hat{k}$

दोनों रेखाओं के मध्य कोण $\theta$ है, इसलिए

$$ \begin{aligned} \cos \theta & =\left|\frac{\vec{b} _{1} \cdot \vec{b} _{2}}{\left|\vec{b} _{1}\right|\left|\vec{b} _{2}\right|}\right|=\left|\frac{(\hat{i}+2 \hat{j}+2 \hat{k}) \cdot(3 \hat{i}+2 \hat{j}+6 \hat{k})}{\sqrt{1+4+4} \sqrt{9+4+36}}\right| \\ & =\left|\frac{3+4+12}{3 \times 7}\right|=\frac{19}{21} \end{aligned} $$

अतः $$ \theta=\cos ^{-1}\left(\frac{19}{21}\right) $$

उदाहरण 8 रेखा-युग्म:

और $$ \begin{aligned} & \frac{x+3}{3}=\frac{y-1}{5}=\frac{z+3}{4} \\ & \frac{x+1}{1}=\frac{y-4}{1}=\frac{z-5}{2} \end{aligned} $$

हल पहली रेखा के दिक्-अनुपात $3,5,4$ और दूसरी रेखा के दिक्-अनुपात $1,1,2$ हैं। यदि उनके बीच का कोण $\theta$ हो तब

$$ \cos \theta=\left|\frac{3.1+5.1+4.2}{\sqrt{3^{2}+5^{2}+4^{2}} \sqrt{1^{2}+1^{2}+2^{2}}}\right|=\frac{16}{\sqrt{50} \sqrt{6}}=\frac{16}{5 \sqrt{2} \sqrt{6}}=\frac{8 \sqrt{3}}{15} $$

अतः अभीष्ट कोण $\cos ^{-1}\left(\frac{8 \sqrt{3}}{15}\right)$ है।

11.5 दो रेखाओं के मध्य न्यूनतम दूरी (Shortest Distance between two lines)

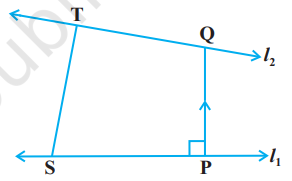
अंतरिक्ष में यदि दो रेखाएँ परस्पर प्रतिच्छेद करती है तो उनके बीच की न्यूनतम दूरी शून्य है। और अंतरिक्ष में यदि दो रेखाएँ समांतर है तो उनके बीच की न्यूनतम दूरी, उनके बीच लंबवत् दूरी होगी अर्थात् एक रेखा के एक बिंदु से दूसरी रेखा पर खींचा गया लंब।

इसके अतिरिक्त अंतरिक्ष में, ऐसी भी रेखाएँ होती है जो न तो प्रतिच्छेदी और न ही समांतर होती है। वास्तव में ऐसी रेखाओं के युग्म $\mathbf{X}^{4}$ असमतलीय होते हैं और इन्हें विषमतलीय रेखाएँ

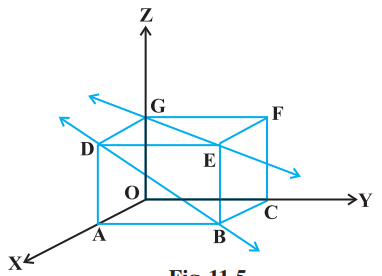
आकृति 11.5 (skew lines) कहते हैं। उदाहरणतया हम आकृति 11.5 में $x, y$ और $z$-अक्ष के अनुदिश क्रमशः $1,3,2$ इकाई के आकार वाले कमरे पर विचार करते हैं।

रेखा GE छत के विकर्ण के अनुदिश है और रेखा $\mathrm{DB}, \mathrm{A}$ के ठीक ऊपर छत के कोने से गुजरती हुई दीवार के विकर्ण के अनुदिश है। ये रेखाएँ विषमतलीय हैं क्योंकि वे समांतर नहीं है और कभी मिलती भी नहीं हैं।

दो रेखाओं के बीच न्यूनतम दूरी से हमारा अभिप्राय एक ऐसे रेखाखंड से है जो एक रेखा पर स्थित एक बिंदु को दूसरी रेखा पर स्थित अन्य बिंदु को मिलाने से प्राप्त हों ताकि इसकी लंबाई न्यूनतम हो। न्यूनतम दूरी रेखाखंड दोनों विषमतलीय रेखाओं पर लंब होगा।

11.5.1 दो विषमतलीय रेखाओं के बीच की दूरी (Distance between two skew lines)

अब हम रेखाओं के बीच की न्यूनतम दूरी निम्नलिखित विधि से ज्ञात करते हैं। मान लीजिए $l _{1}$ और $l _{2}$ दो विषमतलीय रेखाएँ है जिनके समीकरण (आकृति 11.6) निम्नलिखित हैं:

और $$ \begin{align*} \vec{r} & =\vec{a} _{1}+\lambda \vec{b} _{1} \tag{1}\\ \text { } \vec{r} & =\vec{a} _{2}+\mu \vec{b} _{2} \tag{2} \end{align*} $$

रेखा $l _{1}$ पर कोई बिंदु $\mathrm{S}$ जिसकी स्थिति सदिश $\vec{a} _{1}$ और $l _{2}$ पर कोई बिंदु $\mathrm{T}$ जिसकी स्थिति सदिश $\vec{a} _{2}$. है, लीजिए। तब न्यूनतम दूरी सदिश का परिमाण, ST का न्यूनतम दूरी की दिशा में प्रक्षेप की माप के समान होगा (अनुच्छेद 10.6.2)।

यदि $l _{1}$ और $l _{2}$ के बीच की न्यूनतम दूरी सदिश $\overrightarrow{\mathrm{PQ}}$ है तो यह दोनों $\vec{b} _{1}$ और $\vec{b} _{2}$ पर लंब होगी। $\overrightarrow{\mathrm{PQ}}$ की दिशा में इकाई सदिश $\hat{n}$ इस प्रकार होगी कि

आकृति 11.6

$$ \begin{equation*} \hat{n}=\frac{\vec{b} _{1} \times \vec{b} _{2}}{\left|\vec{b} _{1} \times \vec{b} _{2}\right|} \tag{3} \end{equation*} $$

तब $$ \overrightarrow{\mathrm{PQ}}=d $$

जहाँ $d$, न्यूनतम दूरी सदिश का परिमाण है। मान लीजिए $\overrightarrow{\mathrm{ST}}$ और $\overrightarrow{\mathrm{PQ}}$ के बीच का कोण $\theta$ है, तब

परंतु $$ \begin{aligned} \mathrm{PQ} & =\mathrm{ST}|\cos \theta| \\ \cos \theta & =\left|\frac{\overrightarrow{\mathrm{PQ}} \cdot \overrightarrow{\mathrm{ST}}}{|\overrightarrow{\mathrm{PQ}}||\overrightarrow{\mathrm{ST}}|}\right| \\ & \left.=\left|\frac{d \hat{n} \cdot\left(\vec{a} _{2}-\vec{a} _{1}\right)}{d \mathrm{ST}}\right| \text { (क्योंकि } \overrightarrow{\mathrm{ST}}=\vec{a} _{2}-\vec{a} _{1}\right) \\ & =\left|\frac{\left(\vec{b} _{1} \times \vec{b} _{2}\right) \cdot\left(\vec{a} _{2}-\vec{a} _{1}\right)}{\mathrm{ST}\left|\vec{b} _{1} \times \vec{b} _{2}\right|}\right| \text { ((3) के द्वारा) } \end{aligned} $$

इसलिए अभीष्ट न्यूनतम दूरी

या $$ \begin{aligned} & d=\mathrm{PQ}=\mathrm{ST}|\cos \theta| \\ & d=\left|\frac{\left(\vec{b} _{1} \times \vec{b} _{2}\right) \cdot\left(\vec{a} _{2}-\vec{a} _{1}\right)}{\left|\vec{b} _{1} \times \vec{b} _{2}\right|}\right| \text { है। } \end{aligned} $$

कार्तीय रूप (Cartesian Form)

रेखाओं: $$ l _{1}: \frac{x-x _{1}}{a _{1}}=\frac{y-y _{1}}{b _{1}}=\frac{z-z _{1}}{c _{1}} $$

और $$ l _{2}: \frac{x-x _{2}}{a _{2}}=\frac{y-y _{2}}{b _{2}}=\frac{z-z _{2}}{c _{2}} $$

के बीच की न्यूनतम दूरी है: $$ \frac{\left|\begin{array}{ccc} x _{2}-x _{1} & y _{2}-y _{1} & z _{2}-z _{1} \\ a _{1} & b _{1} & c _{1} \\ a _{2} & b _{2} & c _{2} \end{array}\right|}{\sqrt{\left(b _{1} c _{2}-b _{2} c _{1}\right)^{2}+\left(c _{1} a _{2}-c _{2} a _{1}\right)^{2}+\left(a _{1} b _{2}-a _{2} b _{1}\right)^{2}}} $$

11.5.2 समांतर रेखाओं के बीच की दूरी (Distance between parallel lines)

यदि दो रेखाएँ $l _{1}$ यदि $l _{2}$ समांतर हैं तो वे समतलीय होती हैं। माना दी गई रेखाएँ क्रमशः

$$ \begin{align*} & \vec{r}=\vec{a} _{1}+\lambda \vec{b} \tag{1}\\ & \vec{r}=\vec{a} _{2}+\mu \vec{b} \tag{2} \end{align*} $$

हैं, जहाँ $l _{1}$ पर बिंदु $\mathrm{S}$ का स्थिति सदिश $\vec{a} _{1}$ और $l _{2}$ पर बिंदु $\mathrm{T}$ का स्थिति सदिश $\vec{a} _{2}$ है (आकृति 11.7)

क्योंकि $l _{1}$, और $l _{2}$ समतलीय है। यदि बिंदु $\mathrm{T}$ से $l _{1}$ पर डाले गए लंब का पाद $\mathrm{P}$ है तब रेखाओं $l _{1}$ और $l _{2}$ के बीच की दूरी $=|\mathrm{TP}|$

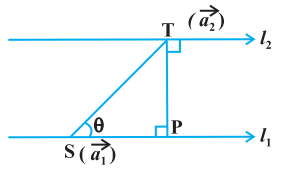
मान लीजिए कि सदिशों $\overrightarrow{\mathrm{ST}}$ और $\vec{b}$ के बीच का कोण $\theta$ है। तब,

$$ \begin{equation*} \vec{b} \times \overrightarrow{\mathrm{ST}}=(|\vec{b}||\overrightarrow{\mathrm{ST}}| \sin \theta) \hat{n} \tag{3} \end{equation*} $$

जहाँ रेखाओं $l _{1}$ और $l _{2}$ के तल पर लंब इकाई सदिश $\hat{n}$ है।

परंतु $$ \overrightarrow{\mathrm{ST}}=\vec{a} _{2}-\vec{a} _{1} $$

इसलिए (3) से हम पाते हैं कि अर्थात् $\quad\left|\vec{b} \times\left(\vec{a} _{2}-\vec{a} _{1}\right)\right|=|\vec{b}| \mathrm{PT} \cdot 1 \quad($ as $|\hat{n}|=1)$ $$ \vec{b} \times\left(\vec{a} _{2}-\vec{a} _{1}\right)=|\vec{b}| \mathrm{PT} \hat{n} \quad(\text { क्योंकि } \mathrm{PT}=\mathrm{ST} \sin \theta) $$

इसलिए ज्ञात रेखाओं के बीच न्यूनतम दूरी

$$ d=|\overrightarrow{\mathrm{PT}}|=\left|\frac{\vec{b} \times\left(\vec{a} _{2}-\vec{a} _{1}\right)}{|\vec{b}|}\right| \text { है। } $$

उदाहरण 9 रेखाओं $l _{1}$ और $l _{2}$ के बीच की न्यूनतम दूरी ज्ञात कीजिए जिनके सदिश समीकरण है :

$$ \begin{aligned} & \vec{r} =\hat{i}+\hat{j}+\lambda(2 \hat{i}-\hat{j}+\hat{k}) \\ \text{ और } \qquad& \vec{r} =2 \hat{i}+\hat{j}-\hat{k}+\mu(3 \hat{i}-5 \hat{j}+2 \hat{k}) \end{aligned} $$

हल समीकरण (1) व (2) की $r=a _{1}+\lambda b _{1}$ और $r=a _{2}+\mu b _{2}$, से तुलना करने पर हम पाते हैं कि

$ \begin{aligned} & a _{1}=\hat{i}+\hat{j}, b _{1}=2 \hat{i}-\hat{j}+\hat{k} \\ & a _{2}=2 \hat{i}+\hat{j}-\hat{k} \text { और } b _{2}=3 \hat{i}-5 \hat{j}+2 \hat{k} \end{aligned} $

इसलिए $\qquad a _{2}-a _{1}=\hat{i}-\hat{k}$

और $\qquad b _{1} \times b _{2}=(2 \hat{i}-\hat{j}+\hat{k}) \times(3 \hat{i}-5 \hat{j}+2 \hat{k})$

$$ =\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k} \\ 2 & -1 & 1 \\ 3 & -5 & 2 \end{array}\right|=3 \hat{i}-\hat{j}-7 \hat{k} $$

इसलिए $$ \left|b _{1} \times b _{2}\right|=\sqrt{9+1+49}=\sqrt{59} $$

इसलिए दी गई रेखाओं के बीच की न्यूनतम दूरी

$$ d=\left|\frac{\left(b _{1} \times b _{2}\right) \cdot\left(a _{2}-a _{1}\right)}{\left|b _{1} \times b _{2}\right|}\right|=\frac{|3-0+7|}{\sqrt{59}}=\frac{10}{\sqrt{59}} $$

उदाहरण 10 निम्नलिखित दी गई रेखाओं $l _{1}$ और $l _{2}$ : $$ \begin{aligned} & \vec{r}=\hat{i}+2 \hat{j}-4 \hat{k}+\lambda(2 \hat{i}+3 \hat{j}+6 \hat{k}) \\ \text{ और } \qquad & \vec{r}=3 \hat{i}+3 \hat{j}-5 \hat{k}+\mu(2 \hat{i}+3 \hat{j}+6 \hat{k}) \end{aligned} $$ के बीच न्यूनतम दूरी ज्ञात कीजिए।

हल दोनों रेखाएँ समातंर हैं। (क्यों?) हमें प्राप्त है कि

$$ a _{1}=\hat{i}+2 \hat{j}-4 \hat{k}, a _{2}=3 \hat{i}+3 \hat{j}-5 \hat{k} \text { और } b=2 \hat{i}+3 \hat{j}+6 \hat{k} $$

इसलिए रेखाओं के बीच की दूरी

$$ \begin{aligned} d & =\left|\frac{b \times\left(a _{2}-a _{1}\right)}{|b|}\right|=\left|\frac{\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k} \\ 2 & 3 & 6 \\ 2 & 1 & -1 \end{array}\right|}{\sqrt{4+9+36}}\right| \\ & =\frac{|-9 \hat{i}+14 \hat{j}-4 \hat{k}|}{\sqrt{49}}=\frac{\sqrt{293}}{\sqrt{49}}=\frac{\sqrt{293}}{7} \text { है। } \end{aligned} $$

प्रश्नावली 11.2

1. दर्शाइए कि दिक्-कोसाइन

$\frac{12}{13}, \frac{-3}{13}, \frac{-4}{13} ; \frac{4}{13}, \frac{12}{13}, \frac{3}{13} ; \frac{3}{13}, \frac{-4}{13}, \frac{12}{13}$ वाली तीन रेखाएँ परस्पर लंबवत् हैं।

2. दर्शाइए कि बिंदुओं $(1,-1,2),(3,4,-2)$ से होकर जाने वाली रेखा बिंदुओं $(0,3,2)$ और $(3,5,6)$ से जाने वाली रेखा पर लंब है।

3. दर्शाइए कि बिंदुओं $(4,7,8),(2,3,4)$ से होकर जाने वाली रेखा, बिंदुओं $(-1,-2,1)$, $(1,2,5)$ से जाने वाली रेखा के समांतर है।

4. बिंदु $(1,2,3)$ से गुज़रने वाली रेखा का समीकरण ज्ञात कीजिए जो सदिश $3 \hat{i}+2 \hat{j}-2 \hat{k}$ के समांतर है।

5. बिंदु जिसकी स्थिति सदिश $2 \hat{i}-j+4 \hat{k}$ से गुज़रने व सदिश $\hat{i}+2 \hat{j}-\hat{k}$ की दिशा में जाने वाली रेखा का सदिश और कार्तीय रूपों में समीकरण ज्ञात कीजिए।

6. उस रेखा का कार्तीय समीकरण ज्ञात कीजिए जो बिंदु $(-2,4,-5)$ से जाती है और $\frac{x+3}{3}=\frac{y-4}{5}=\frac{z+8}{6}$ के समांतर है।

7. एक रेखा का कार्तीय समीकरण $\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2}$ है। इसका सदिश समीकरण ज्ञात कीजिए।

8. निम्नलिखित रेखा-युग्मों के बीच का कोण ज्ञात कीजिए:

(i) $r=2 \hat{i}-5 \hat{j}+\hat{k}+\lambda(3 \hat{i}+2 \hat{j}+6 \hat{k})$ और

$ r=7 \hat{i}-6 \hat{k}+\mu(\hat{i}+2 \hat{j}+2 \hat{k}) $

(ii) $r=3 \hat{i}+\hat{j}-2 \hat{k}+\lambda(\hat{i}-\hat{j}-2 \hat{k})$ और

$ r=2 \hat{i}-\hat{j}-56 \hat{k}+\mu(3 \hat{i}-5 \hat{j}-4 \hat{k}) $

9. निम्नलिखित रेखा-युग्मों के बीच का कोण ज्ञात कीजिए:

(i) $\frac{x-2}{2}=\frac{y-1}{5}=\frac{z+3}{-3}$ और $\frac{x+2}{-1}=\frac{y-4}{8}=\frac{z-5}{4}$

(ii) $\frac{x}{2}=\frac{y}{2}=\frac{z}{1}$ और $\frac{x-5}{4}=\frac{y-2}{1}=\frac{z-3}{8}$

10. $p$ का मान ज्ञात कीजिए ताकि रेखाएँ $\frac{1-x}{3}=\frac{7 y-14}{2 p}=\frac{z-3}{2}$ और $\frac{7-7 x}{3 p}=\frac{y-5}{1}=\frac{6-z}{5}$ परस्पर लंब हों।

11. दिखाइए कि रेखाएँ $\frac{x-5}{7}=\frac{y+2}{-5}=\frac{z}{1}$ और $\frac{x}{1}=\frac{y}{2}=\frac{z}{3}$ परस्पर लंब हैं।

12. रेखाओं के बीच की न्यूनतम दूरी ज्ञात कीजिए:

$\vec{r}=(\hat{i}+2 \hat{j}+\hat{k})+\lambda(\hat{i}-\hat{j}+\hat{k})$ और $\vec{r}=2 \hat{i}-\hat{j}-\hat{k}+\mu(2 \hat{i}+\hat{j}+2 \hat{k})$

13. रेखाओं के बीच की न्यूनतम दूरी ज्ञात कीजिए।

$\frac{x+1}{7}=\frac{y+1}{-6}=\frac{z+1}{1}$ और $\frac{x-3}{1}=\frac{y-5}{-2}=\frac{z-7}{1}$

14. रेखाएँ, जिनके सदिश समीकरण निम्नलिखित है, के बीच की न्यूनतम दूरी ज्ञात कीजिए: $$ \vec{r}=(\hat{i}+2 \hat{j}+3 \hat{k})+\lambda(\hat{i}-3 \hat{j}+2 \hat{k}) \text { और } \vec{r}=4 \hat{i}+5 \hat{j}+6 \hat{k}+\mu(2 \hat{i}+3 \hat{j}+\hat{k}) $$

15. रेखाएँ, जिनकी सदिश समीकरण निम्नलिखित हैं, के बीच की न्यूनतम ज्ञात कीजिए: $$ \vec{r}=(1-t) \hat{i}+(t-2) \hat{j}+(3-2 t) \hat{k} \text { और } \vec{r}=(s+1) \hat{i}+(2 s-1) \hat{j}-(2 s+1) \hat{k} $$

अध्याय 11 पर विविध प्रश्नावली

1. उन रेखाओं के मध्य कोण ज्ञात कीजिए, जिनके दिक्-अनुपात $a, b, c$ और $b-c, c-a$, $a-b$ हैं।

2. $x$-अक्ष के समांतर तथा मूल-बिंदु से जाने वाली रेखा का समीकरण ज्ञात कीजिए।

3. यदि रेखाएँ $\frac{x-1}{-3}=\frac{y-2}{2 k}=\frac{z-3}{2}$ और $\frac{x-1}{3 k}=\frac{y-1}{1}=\frac{z-6}{-5}$ परस्पर लंब हों तो $k$ का मान ज्ञात कीजिए।

4. रेखाओं $\vec{r}=6 \hat{i}+2 \hat{j}+2 \hat{k}+\lambda(\hat{i}-2 \hat{j}+2 \hat{k})$ और $$ \vec{r}=-4 \hat{i}-\hat{k}+\mu(3 \hat{i}-2 \hat{j}-2 \hat{k}) \text { के बीच की न्यूनतम दूरी ज्ञात कीजिए। } $$

5. बिंदु $(1,2,-4)$ से जाने वाली और दोनों रेखाओं

$\frac{x-8}{3}=\frac{y+19}{-16}=\frac{z-10}{7}$ और $\frac{x-15}{3}=\frac{y-29}{8}=\frac{z-5}{-5}$ पर लंब रेखा का सदिश समीकरण ज्ञात कीजिए।

सारांश

• एक रेखा की दिक्-कोसाइन रेखा द्वारा निर्देशांक्षों की धन दिशा के साथ बनाए कोणों की कोसाइन होती है।

• यदि एक रेखा की दिक्-कोसाइन $l, m, n$ हैं तो $l^{2}+m^{2}+n^{2}=1$

• दो बिंदुओं $\mathrm{P}\left(x _{1}, y _{1}, z _{1}\right)$ और $\mathrm{Q}\left(x _{2}, y _{2}, z _{2}\right)$ को मिलाने वाली रेखा की दिक्-कोसाइन $\frac{x _{2}-x _{1}}{\mathrm{PQ}}, \frac{y _{2}-y _{1}}{\mathrm{PQ}}, \frac{z _{2}-z _{1}}{\mathrm{PQ}}$ हैं

जहाँ $\mathrm{PQ}=\sqrt{\left(x _{2}-x _{1}\right)^{2}+\left(y _{2}-y _{1}\right)^{2}+\left(z _{2}-z _{1}\right)^{2}}$

• एक रेखा का दिक्-अनुपात वे संख्याएँ हैं जो रेखा की दिक्-कोसाइन के समानुपाती होती हैं।

• यदि एक रेखा की दिक्-कोसाइन $l, m, n$ और दिक्-अनुपात $a, b, c$ हैं तो

$$ l=\frac{a}{\sqrt{a^{2}+b^{2}+c^{2}}} ; m=\frac{b}{\sqrt{a^{2}+b^{2}+c^{2}}} ; n=\frac{c}{\sqrt{a^{2}+b^{2}+c^{2}}} $$

• विषमतलीय रेखाएँ अंतरिक्ष की वे रेखाएँ जो न तो समांतर हैं और न ही प्रतिच्छेदी हैं। यह रेखाएँ विभिन्न तलों में होती हैं।

• विषमतलीय रेखाओं के बीच का कोण वह कोण है जो एक किसी बिंदु (वरीयता मूल बिंदु की) से विषमतलीय रेखाओं में से प्रत्येक के समांतर खींची गई दो प्रतिच्छेदी रेखाओं के बीच में है।

• यदि $l _{1}, m _{1}, n _{1}$ और $l _{2}, m _{2}, n _{2}$ दिक्-कोसाइन वाली दो रेखाओं के बीच न्यूनकोण $\theta$ है तब

$$ \cos \theta=\left|l _{1} l _{2}+m _{1} m _{2}+n _{1} n _{2}\right| $$

• यदि $a _{1}, b _{1}, c _{1}$ और $a _{2}, b _{2}, c _{2}$ दिक्-अनुपातों वाली दो रेखाओं के बीच का न्यून कोण $\theta$ है तब

$$ \cos \theta=\left|\frac{a _{1} a _{2}+b _{1} b _{2}+c _{1} c _{2}}{\sqrt{a _{1}^{2}+b _{1}^{2}+c _{1}^{2}} \sqrt{a _{2}^{2}+b _{2}^{2}+c _{2}^{2}}}\right| $$

• एक ज्ञात बिंदु जिसकी स्थिति सदिश $\vec{a}$ है से गुज़रने वाली और सदिश $\vec{b}$ के समांतर रेखा का सदिश समीकरण $\vec{r}=\vec{a}+\lambda \vec{b}$ है।

• बिंदु $\left(x _{1}, y _{1}, z _{1}\right)$ से जाने वाली रेखा जिसकी दिक्-कोसाइन $l, m, n$ हैं, का समीकरण $\frac{x-x _{1}}{l}=\frac{y-y _{1}}{m}=\frac{z-z _{1}}{n}$ है।

• दो बिंदुओं जिनके स्थिति सदिश $\vec{a}$ और $\vec{b}$ है से जाने वाली रेखा के समीकरण का सदिश समीकरण $\vec{r}=\vec{a}+\lambda(\vec{b}-\vec{a})$ है।

• यदि दो रेखाओं $\vec{r}=\vec{a} _{1}+\lambda \vec{b} _{1}$ और $\vec{r}=\vec{a} _{2}+\lambda \vec{b} _{2}$, के बीच का न्यूनकोण $\theta$ है तो $\cos \theta=\left|\frac{\vec{b} _{1} \cdot \vec{b} _{2}}{\left|\vec{b} _{1}\right|\left|\vec{b} _{2}\right|}\right|$

• यदि दो रेखाओं $\frac{x-x _{1}}{l _{1}}=\frac{y-y _{1}}{m _{1}}=\frac{z-z _{1}}{n _{1}}$ और $\frac{x-x _{2}}{l _{2}}=\frac{y-y _{2}}{m _{2}}=\frac{z-z _{2}}{n _{2}}$ के बीच का कोण $\theta$ है तब $\cos \theta=\left|l _{1} l _{2}+m _{1} m _{2}+n _{1} n _{2}\right|$.

• दो विषमतलीय रेखाओं के बीच की न्यूनतम दूरी वह रेखाखंड है जो दोनों रेखाओं पर लंब हैं।

• दो रेखाओं $\vec{r}=\vec{a} _{1}+\lambda \vec{b} _{1}$ और $\vec{r}=\vec{a} _{2}+\mu \vec{b} _{2}$ के बीच न्यूनतम दूरी

$$ \left|\frac{\left(\vec{b} _{1} \times \vec{b} _{2}\right) \cdot\left(\vec{a} _{2}-\vec{a} _{1}\right)}{\left|\vec{b} _{1} \times \vec{b} _{2}\right|}\right| \text { है। } $$

• दो रेखाओं $\frac{x-x _{1}}{a _{1}}=\frac{y-y _{1}}{b _{1}}=\frac{z-z _{1}}{c _{1}}$ और $\frac{x-x _{2}}{a _{2}}=\frac{y-y _{2}}{b _{2}}=\frac{z-z _{2}}{c _{2}}$ के बीच न्यूनतम दूरी

$$ \frac{\left|\begin{array}{ccc} x _{2}-x _{1} & y _{2}-y _{1} & z _{2}-z _{1} \\ a _{1} & b _{1} & c _{1} \\ a _{2} & b _{2} & c _{2} \end{array}\right|}{\sqrt{\left(b _{1} c _{2}-b _{2} c _{1}\right)^{2}+\left(c _{1} a _{2}-c _{2} a _{1}\right)^{2}+\left(a _{1} b _{2}-a _{2} b _{1}\right)^{2}}} \text { है। } $$

• दो समांतर रेखाओं $\vec{r}=\vec{a} _{1}+\lambda \vec{b}$ और $\vec{r}=\vec{a} _{2}+\mu \vec{b}$ के बीच की दूरी

$$ \left|\frac{\vec{b} \times\left(\vec{a} _{2}-\vec{a} _{1}\right)}{|\vec{b}|}\right| \text { है। } $$