पूर्व अध्याय में हमने फर्म के उत्पादन फलन तथा लागत वक्रों से संबंधित संकल्पनाओं का अध्ययन किया है। इस अध्याय का केंद्र-बिंदु भिन्न है। यहाँ प्रश्न उठता है कि कोई भी फर्म किस प्रकार यह निर्णय लेती है कि कितना उत्पादन करना है? इस प्रश्न के लिए हमारा उत्तर किसी भी रूप में सरल या अविवादित नहीं है। उत्तर फर्म के व्यवहार की एक निर्णायक अपितु कुछ हद तक अनुचित मान्यता पर आधारित है। हमारे अनुसार फर्म कठोर रूप से लाभ अधिकतमकर्ता होती है। अतः फर्म जिस मात्रा का उत्पादन तथा बाज़ार में उसका विक्रय करती है, वह उसके लाभ को अधिकतम करती है। यहाँ हम यह भी मान लेते हैं कि फर्म जो कुछ वह उत्पादन करती है उसे बेच देती है, इसलिए ‘निर्गत’ और ‘बेची गई मात्र’ को बहुधा अंतपरिवर्तनीय रूप से प्रयोग किया जाता है।

इस पाठ की संरचना निम्नवत् है। हम पहले एक फर्म के अधिकतम लाभ कमाने की समस्या को रखकर उसका विस्तारपूर्वक परीक्षण करते हैं। इसके पश्चात् हम एक फर्म के पूर्ति वक्र का व्युत्पत्ति करते हैं। पूर्ति वक्र निर्गत का वह स्तर दर्शाता है, जिसका चयन एक फर्म बाज़ार कीमत के विभिन्न मूल्यों पर उत्पादन करने के लिए करती है। अंत में हम इस बात का अध्ययन करते हैं कि किस प्रकार व्यक्तिगत फर्मों के पूर्ति वक्रों को समूहित किया जाता है तथा बाज़ार पूर्ति वक्र प्राप्त किया जाता है।

4.1 पूर्ण प्रतिस्पर्धा: पारिभाषिक लक्षण

एक फर्म के लाभ अधिकतमीकरण की समस्या का विश्लेषण करने के क्रम में हमें सबसे पहले बाज़ार का वातावरण, जिसमें फर्म कार्य करती है, को स्पष्ट करना पड़ता है। इस अध्याय में हम एक ऐसे बाज़ार वातावरण का अध्ययन करेंगे जिसे पूर्ण प्रतिस्पर्धा कहा जाता है। एक पूर्णतया प्रतिस्पर्धात्मक बाज़ार में निम्न पारिभाषिक लक्षण होते हैं:

1. बाज़ार में बड़ी संख्या में क्रेता एवं विक्रेता होते हैं।

2. प्रत्येक फर्म एकरूप वस्तु का उत्पादन एवं विक्रय करती है, अर्थात एक फर्म के उत्पाद तथा किसी अन्य फर्म के उत्पाद में भेद नहीं किया जा सकता।

3. फर्मों का बाजार में स्वतंत्र प्रवेश एवं बहिर्गमन होता है।

4. जानकारी पूर्ण होती है।

बड़ी संख्या में क्रेताओं एवं विक्रेताओं की उपस्थिति का अर्थ है कि प्रत्येक क्रेता एवं विक्रेता बाजार के आकार की तुलना में बहुत छोटा होता है। इसका यह अर्थ है कि कोई भी व्यक्तिगत क्रेता अथवा विक्रेता अपने आकार से बाज़ार को प्रभावित नहीं कर सकता। एकरूप उत्पदों का आगे अर्थ है कि प्रत्येक फर्म का उत्पाद समान है। अतः बाज़ार में एक क्रेता किसी भी फर्म से खरीद करने का चुनाव कर सकता है और उसको समान उत्पाद प्राप्त होता है। स्वतंत्र प्रवेश का बहिर्गमन का अर्थ है कि फर्मों का बाजार में प्रवेश करना और साथ ही छोड़ना, सरल होता है। बड़ी संख्या में फर्मों के अस्तित्व के लिए यह शर्त अनिवार्य है। यदि प्रवेश कठिन होता अथवा प्रतिबंधित होता, तो बाज़ार में फर्मों की संख्या थोड़ी हो सकती थी। पूर्ण जानकारी से अभिप्राय है कि सभी क्रेता और विक्रेता उत्पाद की कीमत, गुणवत्ता एवं अन्य सम्बद्ध विवरण से तथा बाज़ार के बारे में पूर्णरूप से सूचित रहते हैं।

यह लक्षण, पूर्ण प्रतियोगिता की एक सर्वाधिक प्रतिष्ठित विशेषता में फलित होते हैं- कीमत स्वीकारक व्यवहार। एक फर्म की दृष्टि से, कीमत-स्वीकारक से क्या अभिप्राय है? एक कीमत-स्वीकारक फर्म को विश्वास है कि यदि वह बाज़ार कीमत से ऊपर एक कीमत निर्धारित करती है, तो यह जिस मात्रा का उत्पादन करती है, उसे बेचने में असमर्थ होगी। दूसरी ओर, यदि निर्धारित कीमत, बाज़ार कीमत के समान अथवा उसकी तुलना में कम हो, तो फर्म जितनी इकाइयाँ विक्रय करने को इच्छुक है, उतना विक्रय कर सकती है। एक ख़रीदार के दृष्टिकोण से, वह किस कीमत को स्वीकार करता है? ख़रीदार निश्चित रूप से सर्वाधिक सम्भावित न्यूनतम कीमत पर वस्तु ख़रीदना चाहती है। तथापि, एक कीमत-स्वीकारक ख़रीदार को यह विश्वास होता है कि यदि उसने बाज़ार कीमत से कम कीमत की माँग की, तो कोई भी फर्म उसे उस वस्तु का विक्रय करने की इच्छुक नहीं होगी। दूसरी ओर, यदि माँगी गई कीमत बाज़ार कीमत के समान अथवा उससे अधिक है, तो ख़रीदार इच्छित मात्रा में वस्तु की बहुत-सी इकाइयाँ प्राप्त कर सकता है।

चूँकि यह अध्याय केवल फर्मों से ही संबंध रखता है, हम ख़रीदार के व्यवहार के विषय में अधिक चर्चा नहीं करेंगे। इसके बावजूद, हम उन स्थितियों की पहचान करेंगे जिनके अंतर्गत कीमत-स्वीकारक फर्मों के लिए एक सार्थक पूर्वधारणा है। कीमत-स्वीकारक ऐसी स्थिति में अक्सर एक सार्थक पूर्वधारक के रूप में जाना जाता है, जब बाज़ार में अनेक फर्में तथा ख़रीदार होते हैं जिन्हें बाज़ार में प्रचलित कीमत की पूर्ण जानकारी है। क्यों? आइए, आरंभ करते हैं एक ऐसी स्थिति से, जहाँ बाज़ार में प्रत्येक फर्म समान (बाज़ार) कीमत लेती है तथा वस्तु की कुछ मात्रा का विक्रय करती है। अब मान लीजिए कि एक विशेष फर्म अपनी कीमत को बाज़ार कीमत की तुलना में बढ़ा देती है। ध्यान दीजिए, चूँकि सभी फर्में एक ही वस्तु का उत्पादन करती हैं तथा सभी ख़रीदार बाज़ार कीमत से पूर्णरूप से अवगत हैं, तो इस प्रश्न पर फर्म अपने ग्राहक खो देगी। इसके अलावा, जैसे-जैसे ये ख़रीदार अन्य फर्मों की ओर रुख करेंगे, कोई ‘समायोजन’ संबंधी समस्या खड़ी नहों होगी। उनकी माँगें तुरंत से पूरी हो जाती हैं, क्योंकि बाज़ार में अनेक फर्में होती हैं। याद कीजिए कि बाज़ार कीमत से अधिक कीमत पर वस्तु की किसी भी मात्रा का विक्रय करने के लिए एक व्यक्तिगत फर्म की असमर्थता बिल्कुल वही है, जो एक कीमत-स्वीकारक की पूर्वधारणा है।

4.2 संप्राप्ति

हमने इंगित किया है कि पूर्ण प्रतिस्पर्धात्मक बाज़ार में एक फर्म को यह विश्वास होता है कि वह बाज़ार कीमत से कम या उसके समान कीमत निर्धारित करके इच्छित मात्रा में किसी भी वस्तु की बहुत-सी इकाइयों का विक्रय कर सकती है। लेकिन, यदि ऐसी स्थिति है, तो निःसंदेह बाज़ार कीमत से कम कीमत निर्धारित करने के लिए कोई भी कारण नहीं है। दूसरे शब्दों में, यदि फर्म वस्तु की कुछ मात्रा का विक्रय करने की इच्छुक है, तो इसके द्वारा निर्धारित कीमत बाज़ार कीमत के बिल्कुल समान होती है।

एक फर्म अपने द्वारा उत्पादित वस्तु का बाज़ार में विक्रय करके संप्राप्ति अर्जित करती है। मान लीजिए वस्तु की एक इकाई की बाज़ार कीमत $p$ है। इसी प्रकार $q$ फर्म की उत्पादित तथा $p$ कीमत पर बेची जानेवाली वस्तु की मात्रा है। तब फर्म की कुल संप्राप्ति वस्तु के बाज़ार मूल्य $(p)$ तथा फर्म के निर्गत $(q)$ के गुणनफल के रूप में परिभाषित की जाती है। अतः

$$ \text { कुल संप्राप्ति }=p \times q $$

तालिका 4.1 कुल संप्राप्ति

इसे स्पष्टता से समझने के लिए निम्नलिखित संख्यात्मक उदाहरण पर ध्यान दें। मान लीजिए कि मोमबत्तियों का बाज़ार पूर्ण रूप से प्रतिस्पर्धात्मक है तथा मोमबत्तियों के एक डिब्बे का बाज़ार कीमत 10 रुपये है। एक मोमबत्ती उत्पादक के लिए कुल संप्राप्ति निर्गत से किस प्रकार संबंधित है, यह तालिका 4.1 दर्शाती है। ध्यान दीजिए कि जब किसी भी डिब्बे का उत्पादन नहीं होता है, तो कुल संप्राप्ति शून्य के बराबर होती है, यदि मोमबत्तियों के एक डिब्बे का उत्पादन होता है, तो कुल संप्राप्ति $1 \times 10$ रुपये $=10$ रुपये के बराबर होती है; यदि मोमबत्तियों के दो डिब्बों का उत्पादन होता है, तो कुल संप्राप्ति $2 \times 10$ रुपये $=20$ रुपये के बराबर होती है तथा इसी प्रकार आगे भी।

कुल संप्राप्ति वक्र : एक फर्म का कुल संप्राप्ति वक्र फर्म द्वारा अर्जित कुल संप्राप्ति तथा फर्म के निर्गत स्तर के बीच संबंध दर्शाती है। वक्र की प्रवणता $A q_{1} / O q_{1}$, बाज़ार कीमत है।

बेचे जाने वाली मात्रा में परिवर्तन से, कुल संप्राप्ति किस प्रकार परिवर्तित होती है को हम एक कुल संप्राप्ति वक्र द्वारा प्रदर्शित कर सकते हैं। कुल संप्राप्ति वक्र अंकित करने में बेची गई मात्रा अथवा निर्गत को $\mathrm{X}$ अक्ष पर और प्राप्त संप्राप्ति को $\mathrm{Y}$ अक्ष पर दिखाते हैं। रेखाचित्र 4.1 एक फर्म की कुल संप्राप्ति वक्र दर्शाती है। यहाँ पर तीन प्रेक्षण प्रासंगिक हैं। पहला, जब निर्गत शून्य हो, फर्म की कुल संप्राप्ति भी शून्य होती है। अतः कुल संप्राप्ति वक्र बिन्दु $\mathrm{O}$ से गुज़रती है। दूसरा, जैसे-जैसे निर्गत बढ़ता है कुल संप्राप्ति में वृद्धि होती है। वैसे भी समीकरण “कुल संप्राप्ति $=p \times q$ " एक सीधी रेखा दर्शाती है, क्योंकि $p$ स्थिर है। इससे अभिप्राय है कि कुल संप्राप्ति वक्र एक ऊपर की ओर जाती हुई सीधी रेखा है। तीसरा, इस सीधी रेखा की प्रवणता पर ध्यान दीजिए। जब निर्गत एक इकाई है (रेखाचित्र 4.1 में समस्तरीय दूरी $O q_{1}$ ) , कुल संप्राप्ति ( रेखाचित्र 4.1 में उर्ध्वस्तरीय ऊँचाई $\left.A q_{1}\right) p \times 1=$ $p$ है। अतः सीधी रेखा की प्रवणता $A q_{1}$ / $O q_{1}=p$ है।

एक फर्म की औसत संप्राप्ति की किसी फर्म की प्रति इकाई निर्गत कुल संप्राप्ति के रूप में परिभाषित किया जाता है। याद कीजिए, यदि किसी फर्म का निर्गत $q$ है तथा बाज़ार कीमत $p$ है, तो कुल संप्राप्ति $p \times q$ के बराबर है। अतः

$$ \text { औसत संप्राप्ति }=\frac{\text { कुल संप्राप्ति }}{q}=\frac{p \times q}{q}=p $$

कीमत रेखा : कीमत रेखा बाज़ार कीमत तथा एक फर्म के निर्गत स्तर के बीच संबंध को दर्शाती है। कीमत रेखा का उध्व्त्तरीय ऊँचाई बाज़ार कीमत, $p$ के बराबर है।

दूसरे शब्दों में, एक कीमत-स्वीकारक फर्म के लिए औसत संप्राप्ति बाज़ार कीमत के बराबर है।

अब रेखाचित्र 4.2 पर ध्यान दीजिए। यहाँ हम एक फर्म के विभिन्न मूल्यों वालें निर्गत ( $x$-अक्ष) के लिए बाज़ार कीमत ( $y$-अक्ष) अंकित करते हैं। चूँकि बाज़ार कीमत $p$ पर स्थिर है, हमें एक समस्तरीय सीधी रेखा प्राप्त होती है जो $y$-अक्ष को $p$ के बराबर ऊँचाई पर काटती है। यह समस्तरीय सीधी रेखा, कीमत रेखा कहलाती है। यहाँ हम औसत संप्राप्ति वक्र अथवा बाज़ार कीमत को ( $y$-अक्ष); फर्म के निर्गत के विभिन्न मूल्यों ( $x$-अक्ष) के लिये दर्शाते हैं। क्योंकि बाज़ार कीमत $p$ पर निश्चित है, हमें एक क्षैतिजीय सीधी रेखा उपलब्ध होती है जो अक्ष के बराबर ऊँचाई पर काटती है। इस क्षैतिजीय सीधी रेखा को कीमत रेखा कहा जाता है। यह पूर्ण स्पर्धा के अन्तर्गत फर्म का औसत वक्र भी होता है। कीमत रेखा, फर्म के माँग वक्र को भी प्रदर्शित करती है। ध्यान दीजिये कि मांग वक्र पूर्णतया लोचदार होता है। इसका अर्थ है कि एक फर्म $p$ कीमत पर वस्तु की जितनी मात्रा चाहे, बेच सकती है।

एक फर्म की सीमांत संप्राप्ति फर्म के निर्गत में प्रति इकाई वृद्धि के लिए कुल संप्राप्ति वृद्धि के रूप में परिभाषित की जाती है। तालिका 4.1 पर पुनः विचार कीजिये। मोमबत्तियों के 2 डिब्बों की बिक्री से कुल संप्राप्ति रु. 20 है। तीन डिब्बों की बिक्री से कुल संप्राप्ति रु. 30 है,

$$ \begin{aligned} \text { सीमांत संप्राप्ति } & =\frac{\text { कुल संप्राप्ति में परिवर्तन }}{\text { मात्रा में परिवर्तन }} \\ & =\frac{30-20}{3-2}=10 \end{aligned} $$

यह एक संयोग ही है कि यह (रु. 10) वही है जो कीमत है। वास्तव में ऐसा नहीं होता। उस स्थिति पर सोचिये, जब फर्म का निर्गत $q_{1}$ से $q_{2}$ हो जाता है। दी गई बाज़ार कीमत $p$ पर,

$$ \text { सीमांत संप्राप्ति,(MR) }=\frac{\left(\mathrm{pq} _{2}-\mathrm{pq} _{1}\right)}{\left(\mathrm{q} _{2}-\mathrm{q} _{1}\right)} $$

$$ \begin{aligned} & =\frac{p\left(q_{2}-q_{1}\right)}{\left(q_{2}-q_{1}\right)} \ & =p \end{aligned} $$

इस प्रकार, पूर्ण स्पर्धा वाली फर्म के लिये $M R=A R=p$

दूसरे शब्दों में, एक कीमत-स्वीकारक फर्म के लिए सीमांत संप्राप्ति बाज़ार कीमत के बराबर होती है।

बीजगणित को अलग रखते हुए, इस परिणाम से अंतर्जान काफी सरल है। जब एक फर्म अपना निर्गत एक इकाई बढ़ाता है, तो यह अतिरिक्त इकाई बाज़ार कीमत पर विक्रय की जाती है। अतः फर्म के द्वारा एक इकाई निर्गत के बढ़ाने से कुल संप्राप्ति में जो वृद्धि होती है, जिसे सीमांत संप्राप्ति कहा जाता है, विशेष रूप से बाज़ार कीमत कहलाती है।

4.3 लाभ अधिकतमीकरण

एक फर्म वस्तु की विशेष मात्रा का उत्पादन तथा विक्रय करती है। फर्म का लाभ जिसे $\pi^{1}$ द्वारा दर्शाया जाता है, इसकी कुल संप्राप्ति तथा इसका कुल उत्पादन लागत के बीच अंतर के रूप में परिभाषित किया जाता है। दूसरे शब्दों में,

$$ \pi=\text { कुल संप्राप्ति - कुल लागत } $$

स्पष्ट रूप से कुल संप्राप्ति तथा कुल लागत के मध्य में अंतर फर्म द्वारा अर्जित की गई निवल लागत है।

एक फर्म अधिकतम लाभ कमाना चाहती है। फर्म मात्रा $q_{0}$ को जिस पर उसके लाभ अधिकतम होते हैं को ज्ञात करना चाहेगी। परिभाषानुसार $q_{0}$ के अतिरिक्त किसी अन्य मात्रा पर, फर्म के लाभ $q_{0}$ की अपेक्षा कम है। समीक्षात्मक प्रश्न यह है: हम $q_{0}$ को किस प्रकार ज्ञात करें?

लाभ अधिकतम होने के लिए $q_{0}$ पर तीन शर्ते पूर्ण होनी चाहिए:

1. कीमत $p$, सीमांत लागत के बराबर हो।

2. $q_{0}$ पर सीमांत लागत ह्रासमान नहीं हो।

3. फर्म को उत्पादन करते रहने के लिए अल्पकाल में, कीमत, औसत परिवर्तनीय लागत से अधिक हो ( $\mathrm{p}>\mathrm{AVC}$ ) दीर्घकाल में कीमत औसत लागत से अधिक हो $(\mathrm{p}>\mathrm{AC})$ ।

4.3.1 स्थिति 1

लाभ, कुल संप्राप्ति तथा कुल लागत का अंतर होता है। जैसे निर्गत में वृद्धि होती है कुल संप्राप्ति तथा कुल लागत में भी वृद्धि होती है। जब तक कुल संप्राप्ति में वृद्धि कुल लागत में परिवर्तन से अधिक है, लाभ में लगातार वृद्धि होगी। याद करें कि निर्गत में प्रति इकाई वृद्धि के कारण, कुल संप्राप्ति, में परिवर्तन सीमांत लागत होती है। अतः हम इस निष्कर्ष पर पहुँचते हैं कि जब तक सीमांत संप्राप्ति, लागत से अधिक है, लाभ बढ़ते हैं। इसी तर्क के आधार पर, जब तक सीमांत संप्राप्ति, सीमांत लागत से कम है, लाभ कम होंगे। इसका अर्थ यह है कि, लाभों को अधिकतम होने के लिए, सीमांत संप्राप्ति, सीमांत लागत के बराबर होनी चाहिए।[^8]

दूसरे शब्दों में, लाभ, उत्पादन के उस स्तर पर (जिसे हमने $q_{0}$ कहा है) अधिकतम होते हैं। जिस पर $\mathrm{MR}=\mathrm{MC}$

हमने यह स्थापित कर दिया है कि एक पूर्ण तथा प्रतिस्पर्धात्मक फर्म के लिए MR=P इसलिए, फर्म का लाभ-अधिकतमीकरण निर्गत वह निर्गत है जिस पर $\mathrm{P}=\mathrm{MC}$ हो।

4.3.2 स्थिति 2

दूसरी स्थिति को लीजिए, जिसका लागू होना निर्गत स्तर का लाभ अधिकतमीकरण सकारात्मक होने के लिए आवश्यक है। ऐसी स्थिति क्यों है कि निर्गत स्तर पर लाभ अधिकतमीकरण सीमांत लागत वक्र की प्रवणता नीचे की ओर नहीं हो सकती? इस प्रश्न का उत्तर देने के लिए एक बार फिर रेखाचित्र 4.3 को देखें। ध्यान दीजिये कि $q_{1}$ तथा $q_{4}$ निर्गत स्तरों पर, बाजार कीमत, सीमांत लागत के बराबर है। जैसे, $q_{1}$ निर्गत स्तर, सीमांत लागत वक्र नीचे की ओर प्रवण है। हम कहते हैं कि $q_{1}$ निर्गत स्तर का लाभ अधिकतमीकरण नहीं हो सकता। क्यों?

लाभ अधिकतमीकरण के लिए स्थितियाँ 1 तथा 2 : यह चित्र यह दर्शाने के लिए उपयोग में लाया गया है कि जब बाज़ार कीमत $p$ है, तो एक लाभ-अधिकतमीकरण करने वाली फर्म का निर्गत स्तर $q_{1}$ (सीमांत लागत वक्र $M C$ की प्रवणता नीचे की और है)। $q_{2}$ और $q_{3}$ (बाज़ार कीमत सीमांत लागत से अधिक है) या $q_{5}$ और $q_{6}$ (सीमांत लागत बाज़ार कीमत से अधिक है) नहीं हो सकता।

प्रेक्षण कीजिए कि $q_{1}$ से थोड़ी-सी बायों ओर सभी निर्गत स्तरों के लिए बाज़ार कीमत सीमांत लागत की तुलना में कम है। परन्तु भाग 4.3 .1 की स्थिति 2 में दिए गए तर्क से निश्चित रूप से अभिप्राय है कि $q_{1}$ से थोड़े-से कम निर्गत स्तर पर, फर्म का लाभ समवर्ती निर्गत स्तर पर $q_{1}$ से आगे निकल जाता है। यह स्थिति होते हुए $q_{1}$ निर्गत स्तर का एक लाभ अधिकतमीकरण नहीं हो सकता।

लाभ अधिकतमीकरण के साथ कीमत, औसत परिवर्ती लागत के बीच संबंध (अल्पकाल): रेखाचित्र को यह दर्शाने के लिए उपयोग किया गया है कि एक लाभ-अधिकतमीकरण करने वाली फर्म अल्पकालिक स्थिति में शून्य निर्गत का उत्पादन करती है, जहाँ बाज़ार कीमत $p$ इसकी न्यूनतम औसत परिवर्ती लागत की तुलना में कम होती है। यदि फर्म का निर्गत स्तर $q_{1}$ है, तो फर्म को कुल परिवर्त्ती लागत इसकी संप्राप्ति से आयत PEBA के क्षेत्रफल के समान मात्रा में अधिक है।

4.3.3 स्थिति 3

उस तृतीय स्थिति पर ध्यान दीजिए, जिसका लाभ अधिकतमीकरण निर्गत स्तर के सकारात्मक होने की स्थिति में लागू होना आवश्यक है। ध्यान दीजिए कि तीसरी स्थिति के दो भाग हैं: एक भाग अल्पकालीन स्थिति में तथा दूसरा, दीर्घकालीन स्थिति में लागू होता है।

स्थिति 1: अल्पकालीन स्थिति में कीमत को औसत परिवर्ती लागत की तुलना में अधिक अथवा समान होनी चाहिए।

हम यह दर्शाएँगे कि स्थिति 1 (ऊपर देखिए) का वक्तव्य सही है, इस तर्क के साथ कि अल्पकालीन स्थिति में एक लाभ-अधिकतमीकरण करने वाली फर्म किसी ऐसे निर्गत स्तर पर उत्पादन नहीं करेगी, जहाँ बाज़ार कीमत औसत परिवर्ती लागत की तुलना में कम हो।

आइए, अब रेखाचित्र 4.4 की ओर रुख़ करें। निरीक्षण कीजिए कि निर्गत स्तर $q_{1}$ पर बाज़ार कीमत $p$, औसत परिवर्ती लागत की तुलना में कम है। हम यह दावा करते हैं कि $q_{1}$ निर्गत स्तर का एक लाभ-अधिकतमीकरण नहीं हो सकता। क्यों?

ध्यान दीजिए कि $q_{1}$ पर फर्म की कुल संप्राप्ति निम्नलिखित है :

कुल संप्राप्ति $=$ कीमत $\times$ मात्रा

$=$ उर्ध्वस्तरीय ऊँचाई $O_{\mathrm{P}} \times$ चौड़ाई $O q_{1}$

$=$ आयत $O p A q_{1}$ का क्षेत्रफल

समान रूप से, फर्म की कुल परिवर्त्री लागत $q_{1}$ पर निम्नलिखित है :

कुल परिवर्ती लागत $=$ औसत परिवर्त्री लागत $\times$ मात्रा

$$ \begin{aligned} & =\text { ऊर्ध्वस्तरीय ऊँचाई } O E \times \text { चौड़ाई } O q_{1} \ & =\text { आयत } O E B q_{1} \text { का क्षेत्रफल } \end{aligned} $$

अब याद कीजिए कि $q_{1}$ पर फर्म का लाभ कुल प्राप्ति - (कुल परिवर्ती लागत + कुल स्थिर लागत) है; अर्थात् [आयत $O p A q_{1}$ का क्षेत्रफल]-[आयत $O E B q_{1}$ का क्षेत्रफल]- कुल स्थिर लागत। यदि फर्म शून्य निर्गत का उत्पादन करती है, तो क्या होता है? क्योंकि निर्गत शून्य है, कुल संप्राप्ति तथा कुल परिवर्ती लागत भी शून्य हैं। अतः शून्य निर्गत पर फर्म का लाभ कुल स्थिर लागत के समान है। परंतु, आयत $O p A q_{1}$ का क्षेत्रफल आयत $O E B q_{1}$ के क्षेत्रफल से स्पष्ट रूप से कम है। अतः $\mathrm{q}_{1}$ पर फर्म का लाभ है (क्षेत्रफल EBAp) $\mathrm{TFC}$, जोकि नियमबद्ध रूप से उससे कम है जो वह कुछ भी उत्पादन न करने पर प्राप्त करती। अतः फर्म कुछ भी उत्पादन नहीं चाहेगी और बाज़ार से बर्हिगमन कर जायेगी।

स्थिति 2 : दीर्घकाल में कीमत को औसत लागत की तुलना में अधिक अथवा समान होना चाहिए।

दीर्घकाल में एक लाभ-अधिकतमीकरण करने वाली फर्म किसी ऐसे निर्गत स्तर पर उत्पादन नहीं करेगी, जहाँ बाज़ार कीमत औसत लागत की तुलना में कम हो।

आइए, रेखाचित्र 4.5 को देखें। निरीक्षण कीजिए कि निर्गत स्तर q_1 पर बाज़ार कीमत p (दीर्घकाल) औसत लागत की तुलना में कम है। हम दावा करते हैं कि $q_1$ एक लाभ-अधिकतमीकरण निर्गत स्तर नहीं हो सकता। क्यों?

कीमत-औसत लागत का कीमत अधिकतमीकरण (दीर्घकालीन) के साथ संबंधः रेखाचित्र का उपयोग यह दर्शाने के लिए किया गया है कि कीमत-अधिकतमीकरण करने वाली फर्म दीर्घकाल में शून्य निर्गत का उत्पादन करती है जब बाज़ार कीमत इसकी न्यूनतम दीर्घकालीन औसत लागत से कम है। यदि फर्म का निर्गत स्तर $q_{1}$ है, फर्म को कुल लागत इसकी संप्राप्ति से अधिक है एक ऐसी मात्रा में, जो आयत $p E B A$ के क्षेत्रफल के समान है।

ध्यान दीजिए कि फर्म की कुल संप्राप्ति, $q_{1}$ पर आयत $O p A q_{1}$ का क्षेत्रफल (कीमत तथा मात्रा का गुणनफल) जब तक कि फर्म की कुल लागत आयत $O E B q_{1}$ का क्षेत्रफल (औसत लागत तथा मात्रा का गुणनफल) है। चूंकि आयत $O E B q_{1}$ का क्षेत्रफल आयत $O p A q_{1}$ के क्षेत्रफल से अधिक है, निर्गत स्तर $q_{1}$ पर फर्म हानि उठाती है। परन्तु दीर्घकालीन स्थिति में एक फर्म, यदि उत्पादन बंदी कर देती है, शून्य लाभ प्राप्त करती है। इस स्थिति में फर्म पुनः बहिर्गमन करना पसंद करती है।

4.3.4 लाभ अधिकतमीकरण समस्याः आरेख द्वारा प्रदर्शन

आइए $3.1,3.2,3.3$ खंडों में दी गई सामग्री का उपयोग कर हम अल्पकाल में एक फर्म की लाभ अधिकतमीकरण समस्या को आरेख द्वारा प्रदर्शित करते हैं। रेखाचित्र 4.6 पर विचार कीजिए। इसमें बाज़ार कीमत $p$ है। बाज़ार कीमत को (अल्पकाल) सीमांत लागत के बराबर करके हमें $q_{0}$ निर्गत स्तर प्राप्त होता है। $q_{0}$ पर, अल्पकालीन सीमांत लागत की प्रवणता ऊपर की ओर जा रही है तथा $p$, औसत परिवर्ती लागत से अधिक है। क्योंकि $q_{0}$ पर $3.1,3.3$ खंडों में चर्चित शर्ते पूरी हो जाती हैं, हम यह कहेंगे कि फर्म का लाभ-अधिकतमीकरण निर्गत स्तर $q_{0}$ है।

लाभ-अधिकतमीकरण का आरेख द्वारा प्रदर्शन (अल्पकाल): दी हुई बाज़ार कीमत $p$ पर एक लाभ अधिकतम करने वाली फर्म का निर्गत स्तर $q_{0}$ है। $q_{0}$ पर फर्म का लाभ आयत EpAB के क्षेत्रफल के बराबर है।

$q_{0}$ पर क्या होता है? $q_{0}$ पर फर्म की कुल संप्राप्ति आयत $O P A q_{0}$ का क्षेत्रफल (कीमत तथा मात्रा का उत्पाद) है जबकि $q_{0}$ पर कुल लागत आयत $O E B q_{0}$ का क्षेत्रफल (अल्पकालीन औसत लागत तथा मात्रा का उत्पाद) है। अतः $q_{0}$ पर, फर्म आयत $E p A B$ के क्षेत्रफल के बराबर लाभ अर्जित करती है।

4.4 एक फर्म का पूर्ति वक्र

एक फर्म की ‘पूर्ति’ वह मात्रा है जो वह एक दी गई कीमत, प्रौद्योगिकी तथा उत्पादन कारकों की कीमतों पर बेचने का निर्णय लेती है। एक तालिका जो विभिन्न कीमतों पर प्रौद्योगिकी तथा कारकों की कीमतें अपरिवर्तित रहने पर, एक फर्म की बेचे जाने वाली मात्राओं का विवरण देती है, ‘पूर्ति सारणी’ कहते हैं। हम इसे ग्राफ पर भी प्रदर्शित कर सकते हैं जिसे ‘पूर्ति वक्र’ कहते हैं। एक फर्म का पूर्ति वक्र निर्गत के स्तरों ( $x$-अक्ष पर अंकित) को दर्शाता है जिनका संबंधित फर्म बाज़ार कीमत के विभिन्न मूल्यों पर ( $y$-अक्ष पर अंकित) उत्पादन के लिए चयन करती है, पुन: प्रौद्योगिकी और उत्पादन कारकों की कीमतों को दी हुई मानकर। एक दिए हुए बाज़ार के लिए, एक लाभ-अधिकतमीकरण फर्म का उत्पादन स्तर इस पर निर्भर करेगा कि हम अल्पकाल पर विचार कर रहे हैं अथवा दीर्घकाल पर। इसी के अनुसार, हम अल्पकालीन पूर्ति वक्र तथा दीर्घकालीन पूर्ति वक्र में भेद करते हैं।

4.4.1 एक फर्म का अल्पकालीन पूर्ति वक्र

रेखाचित्र 4.7 को देखते हैं तथा फर्म का अल्पकालीन पूर्ति वक्र व्युत्पन्न करते हैं। इसे हम दो भागों में विभाजित करेंगे। प्रथम, हम फर्म के निर्गत स्तर का लाभ-अधिकतमीकरण निर्धारण करते हैं जबकि बाज़ार कीमत न्यूनतम औसत परिवर्ती लागत से अधिक अथवा उसके बराबर है। इसके पश्चात् फर्म के निर्गत स्तर का लाभ-अधिकतमीकरण निर्धारण करते हैं, जबकि बाज़ार कीमत न्यूनतम औसत परिवर्ती लागत से कम है।

विभिन्न बाज़ार मूल्यों के लिए अल्पकाल में लाभअधिकतमीकरणः रेखाचित्र बाज़ार कीमत के दो मूल्यों $p_{1}$ तथा $p_{2}$ के लिए अल्पकाल में लाभ-अधिकतमीकरण फर्म द्वारा चयनित निर्गत स्तर को दर्शाता है। जब बाज़ार कीमत $p_{1}$ है, तो फर्म का निर्गत स्तर $q_{1}$ है तथा जब बाज़ार कीमत $p_{2}$ है, तो फर्म शून्य निर्गत का उत्पादन करती है।

स्थिति 1: कीमत न्यूनतम औसत परिवर्ती लागत से अधिक अथवा उसके बराबर मान लीजिए कि बाज़ार कीमत $p_{1}$ है जो न्यूनतम औसत परिवर्ती लागत से अधिक है। हम $p_{1}$ को अल्पकालीन कीमत वक्र के बढ़ते भाग की बराबरी से शुरू करते हैं; इससे हमें निर्गत स्तर $q_{1}$ प्राप्त होता है। यह भी ध्यान दें कि $q_{1}$ पर औसत परिवर्ती लागत बाज़ार कीमत $p_{1}$ से अधिक नहीं है। इस प्रकार खंड 3 में चर्चित तीनों शर्तें $q_{1}$ पर पूरी हो जाती हैं। अतः जब बाज़ार कीमत $p_{1}$ है, तो फर्म का अल्पकाल में निर्गत स्तर $q_{1}$ के बराबर है।

स्थिति 2 : कीमत न्यूनतम औसत परिवर्ती लागत से कम

मान लीजिए, बाज़ार कीमत $p_{2}$ है जो कि न्यूनतम औसत परिवर्ती लागत से कम है। हमने तर्क दिया है (खंड 3 में शर्त 3 को देखिए) कि यदि एक लाभ-अधिकतमीकरण फर्म अल्पकाल में एक सकारात्मक निर्गत का उत्पादन करती है, तो उस निर्गत स्तर पर बाज़ार कीमत $p_{2}$ औसत परिवर्ती लागत से अधिक अथवा बराबर होनी चाहिए। किंतु रेखाचित्र 4.7 में हम देखते हैं कि सभी सकारात्मक निर्गत स्तरों पर औसत परिवर्ती लागत स्पष्ट रूप से $p_{2}$ से अधिक है। दूसरे शब्दों में, यह संभव नहीं है कि फर्म एक सकारात्मक निर्गत की पूर्ति करे। अतः यदि बाज़ार कीमत $p_{2}$ है, तो फर्म शून्य निर्गत का उत्पादन करेगी।

एक फर्म का अल्पकालीन पूर्ति वक्रः एक फर्म का अल्पकालीन पूर्ति वक्र, जो इसके अल्पकालीन सीमांत लागत वक्र तथा औसत परिवर्त्ती लागत वक्र पर आधारित है, जिसे मोटी रेखा द्वारा प्रदर्शित किया गया है।

स्थिति 1 तथा 2 को मिलाकर हम एक महत्त्वपूर्ण निष्कर्ष पर पहुँचते हैं। एक फर्म का अल्पकालीन पूर्ति वक्र न्यूनतम औसत परिवर्ती लागत से ऊपर अल्पकालीन कीमत वक्र का बढ़ता हुआ भाग होता है तथा न्यूनतम औसत परिवर्ती लागत से कम सभी कीमतों पर निर्गत शून्य होता है। रेखाचित्र 4.8 में फर्म के अल्पकालीन पूर्ति वक्र को मोटी रेखा से दर्शाया गया है।

4.4.2 एक फर्म का दीर्घकालीन पूर्ति वक्र

आइए, रेखाचित्र 4.9 को देखते हैं तथा फर्म के दीर्घकालीन पूर्ति वक्र की व्युत्पत्ति करते हैं। अल्पकालीन स्थिति की भाँति, हम इस व्युत्पत्ति को दो भागों में विभाजित करते हैं। पहले हम फर्म के निर्गत स्तर का लाभअधिकतमीकरण निर्गत स्तर निर्धारित करते हैं, जब बाज़ार कीमत न्यूनतम (दीर्घकालीन) औसत लागत से अधिक अथवा उसके बराबर हो। तत्पश्चात्, हम फर्म वे निर्गत स्तर का लाभ-अधिकतमीकरण निर्धारण करेंगे, जब बाज़ार कीमत न्यूनतम (दीर्घकालीन) औसत लागत से कम हो।

विभिन्न बाज़ार कीमत के मूल्यों पर दीर्घकाल में लाभअधिकतमीकरण: रेखाचित्र एक लाभ-अधिकतमीकरण फर्म द्वारा चयनित निर्गत स्तरों को बाज़ार कीमत के दो विभिन्न मूल्यों $p_{1}$ तथा $p_{2}$ को दीर्घकाल में दर्शाता है। जब बाज़ार कीमत $p_{1}$ है, फर्म का निर्गत स्तर $q_{1}$ है; जब बाज़ार कीमत $p_{2}$ है, तो फर्म शून्य निर्गत का उत्पादन करती है।

स्थिति 1: कीमत न्यूनतम दीर्घकालीन औसत लागत से अधिक अथवा बराबर है। मान लीजिए, बाज़ार कीमत $p_{1}$ है जो न्यूनतम दीर्घकालीन औसत लागत से अधिक है। $p_{1}$ पर बराबर करके दीर्घकालीन सीमांत लागत के साथ दीर्घकालीन सीमांत लागत वक्र के बढ़ते हुए भाग को करने से हमें निर्गत स्तर $q_{1}$ प्राप्त होता है। यह भी ध्यान दीजिए कि $q_{1}$ पर दीर्घकालीन औसत लागत बाज़ार कीमत $p_{1}$ से अधिक नहीं होता। अतः सभी तीन शर्तें जिन पर खंड 3 में प्रकाश डाला गया है, $q_{1}$ पर संतुष्ट होती हैं। अतः जब बाज़ार कीमत $p_{1}$ है, तो फर्म दीर्घकाल में $q_{1}$ के बराबर निर्गत की पूर्ति करती है।

स्थिति 2 : कीमत न्यूनतम दीर्घकालीन औसत लागत से कम

मान लीजिए, बाज़ार कीमत $p_{2}$ है, जो न्यूनतम दीर्घकालीन औसत लागत से कम है। हमने तर्क दिया है (खंड 3 में शर्त 3 देखिए) कि यदि एक लाभ-अधिकतमीकरण फर्म दीर्घकालीन स्थिति में एक सकारात्मक निर्गत का उत्पादन करती है, तो बाज़ार कीमत $p_{2}$ उस निर्गत स्तर पर दीर्घकालीन औसत लागत से अधिक अथवा उसके बराबर होती है। परंतु रेखाचित्र 4.9 में देखिए कि सभी सकारात्मक निर्गत स्तरों के लिए दीर्घकालीन औसत लागत $p_{2}$ से स्पष्ट अधिक है। दूसरे शब्दों में, यह स्थिति संभव नहीं है कि फर्म एक सकारात्मक निर्गत की पूर्ति करे। अतः जब बाज़ार कीमत $p_{2}$ है, तो फर्म शून्य निर्गत का उत्पादन करती है।

स्थिति 1 तथा 2 को मिलाकर हम एक महत्त्वपूर्ण निष्कर्ष पर पहुँचते हैं। एक फर्म का दीर्घकालीन पूर्ति वक्र दीर्घकालीन औसत लागत के बराबर अथवा उससे ऊपर दीर्घकालीन सीमांत

लागत वक्र का बढ़ता हुआ भाग है, लेकिन न्यूनतम दीर्घकालीन औसत लागत से कम सभी कीमतों पर निर्गत शून्य है। रेखाचित्र 4.10 में दीर्घकालीन पूर्ति वक्र को मोटी रेखा से दर्शाया गया है।

एक फर्म का दीर्घकालीन पूर्ति वक्रः एक फर्म का दीर्घकालीन पूर्ति वक्र जो दीर्घकालीन सींमांत लागत वक्र तथा दीर्घकालीन औसत लागत वक्र पर आधारित है, मोटी रेखा द्वारा दर्शाया गया है।

4.4.3 उत्पादन बंदी बिंदु

इससे पूर्व पूर्ति वक्र ज्ञात करते समय हमने यह विवेचना की थी कि अल्पकाल में फर्म तब तक उत्पादन जारी रखती है, जब तक कीमत न्यूनतम औसत परिवर्ती लागत की तुलना में अधिक अथवा उसके बराबर होती है। हम पूर्ति वक्र पर जब नीचे की ओर चलते हैं, तो अंतिम कीमत-निर्गत संयोग जिस पर फर्म सकारात्मक निर्गत का उत्पादन करती है, वह न्यूनतम औसत परिवर्ती लागत बिंदु है, जहाँ अल्पकालीन सीमांत लागत वक्र औसत परिवर्ती लागत वक्र को काटता है। इसके नीचे, कोई उत्पादन नहीं होगा। यह बिंदु फर्म का अल्पकालीन उत्पादन बंदी बिंदु कहलाता है। तथापि, दीर्घकालीन स्थिति में, उत्पादन बंदी बिंदु न्यूनतम दीर्घकालीन औसत लागत वक्र है।

4.4.4 सामान्य लाभ तथा लाभ-अलाभ बिंदु

लाभ के न्यूनतम स्तर को जो एक फर्म को इसके वर्तमान व्यापार में बनाए रखने के लिए आवश्यक है, सामान्य लाभ कहकर परिभाषित करते हैं। एक फर्म जो सामान्य लाभ अर्जित नहीं करती, व्यापार में नहीं रह सकती। सामान्य लाभ, फर्म की कुल लागतों का एक भाग होता है। इन्हें उद्यमशीलता की अवसर लागत के रूप में समझना भी लाभदायक है। वह लाभ जो एक फर्म सामान्य लाभ से ऊपर अर्जित करती है, अधिसामान्य लाभ कहलाता है। दीर्घकालीन स्थिति में यदि फर्म सामान्य लाभ से कुछ भी कम अर्जित करती है, तो वह उत्पादन नहीं करती है। किंतु अल्पकाल में फर्म का लाभ यदि इस स्तर से कम है, तो भी उत्पादन कर सकती है। पूर्ति वक्र के जिस बिंदु पर एक फर्म केवल साधारण लाभ अर्जित करती है, वह फर्म का लाभ-अलाभ बिंदु कहलाता है। अतः न्यूनतम औसत लागत का वह बिंदु जिस पर पूर्ति वक्र दीर्घकालीन औसत वक्र (अल्पकाल में अल्पकालीन औसत लागत वक्र) को काटता है, फर्म का लाभ-अलाभ बिंदु है।

अवसर लागत

अर्थशास्त्र में अवसर लागत की संकल्पना का प्रयोग मिलता है। किसी कार्य की अवसर लागत दूसरे सर्वश्रेष्ठ कार्य से प्राप्त त्यागा गया लाभ है। मान लीजिए, आपके पास 1,000 रुपये हैं जिन्हें आप अपने पारिवारिक व्यवसाय में निवेश करने का निर्णय लेते हैं। आपके कार्य की अवसर लागत क्या है? यदि आप इस राशि का निवेश नहीं करते, तो आप या तो इसे घर की तिजोरी में रख सकते हैं, जिससे आपको शून्य प्रतिफल प्राप्त होगा अथवा आप इसे बैंक-1 या बैंक- 2 में जमा करा सकते हैं, जिस स्थिति में आपको क्रमशः 10 प्रतिशत अथवा 5 प्रतिशत ब्याज प्राप्त होता है। अतः वैकल्पिक क्रियाओं से जो अधिकतम लाभ आप अर्जित कर सकते हैं, वह बैंक 1 द्वारा दिया गया ब्याज है। परंतु यदि आप इस धन का अपने पारिवारिक व्यवसाय में निवेश करते हैं, तो यह विकल्प समाप्त हो जाएगा। अतः आपके पारिवारिक व्यवसाय में धन निवेश करने की अवसर लागत बैंक- 1 से प्राप्त ब्याज की राशि का त्याग है।

4.5 फर्म के पूर्ति वक्र के निर्धारक तत्त्व

पूर्व खंड में हमने देखा कि एक फर्म का पूर्ति वक्र उसके सीमांत लागत वक्र का भाग है। अतः कोई भी कारक, जो एक फर्म के सीमांत लागत वक्र को प्रभावित करता हो, इसके पूर्ति वक्र का निर्धारक होता है। इस भाग में, हम ऐसे तीन कारकों की चर्चा करेंगे।

4.5.1 प्रौद्योगिकीय प्रगति

मान लीजिए, एक फर्म निश्चित वस्तुओं के उत्पादन के लिए उत्पादन के दो कारकों-पूँजी तथा श्रम का उपयोग करती है- फर्म द्वारा संगठनात्मक नवप्रवर्तन के पश्चात्, पूँजी तथा श्रम के उसी स्तर से अब निर्गत की अधिक इकाइयों का उत्पादन होता है। दूसरे शब्दों में, एक निश्चित निर्गत स्तर का उत्पादन करने के लिए संगठनात्मक नव प्रवर्तन के कारण फर्म आगतों की कम इकाइयाँ उपयोग करती है। यह अपेक्षित है कि निर्गत के किसी भी स्तर पर यह फर्म की सीमांत लागत को कम करेगा। कुल सीमांत लागत वक्र की दाहिनी ओर (अथवा नीचे की ओर) शिफ्ट है। चूँकि फर्म का पूर्ति वक्र अनिवार्य रूप से सीमांत लागत वक्र का एक भाग है, प्रौद्योगिकीय प्रगति फर्म के पूर्ति वक्र को दाहिनी ओर शिफ्ट करती है। किसी भी दी हुई बाज़ार कीमत पर, फर्म अब निर्गत की अधिक इकाइयों की पूर्ति करती है।

4.5.2 आगत कीमतें

आगत कीमतों में परिवर्तन फर्म के पूर्ति वक्र को भी प्रभावित करता है। यदि एक आगत की कीमत (जैसे, श्रम की मज़दूरी दर) में वृद्धि होती है, उत्पादन लागत बढ़ जाती है। निर्गत के किसी भी स्तर पर फर्म की औसत लागत के परिणामस्वरूप वृद्धि, सामान्यतः निर्गत के किसी भी स्तर पर फर्म की सीमांत लागत में वृद्धि के साथ होती है, अर्थात् अब सीमांत लागत वक्र में बायों ओर (अथवा ऊपर की ओर) शिफ्ट करती है। इससे अभिप्राय है कि फर्म का पूर्ति वक्र बायों ओर शिफ्ट हो जाता है: किसी भी बाज़ार कीमत पर अब फर्म निर्गत की कम इकाइयों की पूर्ति करती है।

प्रति वक्र पर इकाई कर का प्रभाव

इकाई कर वह कर है जो सरकार निर्गत के प्रति इकाई विक्रय पर लगाती है। उदाहरण के लिए, मान लीजिए कि सरकार द्वारा लगाया गया इकाई कर 2 रुपये है, तो यदि फर्म वस्तु की 10 इकाइयों का उत्पादन तथा विक्रय करती है, तो कुल कर जो फर्म को सरकार को चुकाना पड़ेगा, $10 \times 2$ रुपये $=20$ रुपये है।

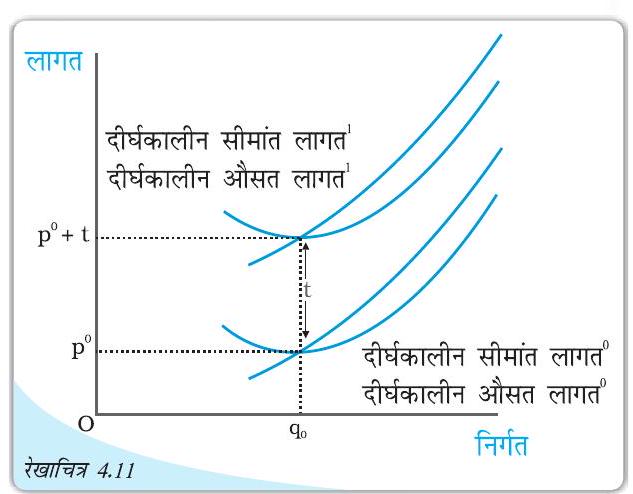
लागत वक्र तथा इकाई कर: दीर्घकालीन औसत लागत ${ }^{\circ}$ तथा दीर्घकालीन सीमांत लागत ${ }^{\circ}$, क्रमशः इकाई कर लगने से पूर्व एक फर्म के दीर्घकालीन औसत लागत वक्र तथा दीर्घकालीन सीमांत लागत वक्र हैं। $t$ रुपये प्रति इकाई कर लगने के पश्चात्, दीर्घकालीन औसत लागत ${ }^{1}$ तथा दीर्घकालीन सीमांत लागत ${ }^{\prime}$ क्रमशः एक फर्म के दीर्घकालीन औसत लागत वक्र तथा दीर्घकालीन सीमांत लागत वक्र हैं।

इकाई कर लगाने से एक फर्म के दीर्घकालीन पूर्ति वक्र में किस प्रकार परिवर्तन होता है? आइए, रेखाचित्र 4.11 को देखें। इकाई कर लगने से पूर्व दीर्घकालीन सीमांत लागत तथा

दीर्घकालीन औसत लागत क्रमशः फर्म की दीर्घकालीन सीमांत लागत वक्र ${ }^{0}$ तथा दीर्घकालीन औसत लागत वक्र ${ }^{0}$ हैं। अब, मान लीजिए कि सरकार $t$ रुपये इकाई कर लगा देती है। क्योंकि फर्म को आवश्यक रूप से वस्तु की प्रत्येक उत्पादित इकाई के लिए $t$ रुपये अतिरिक्त देने पड़ रहे हैं, फर्म की निर्गत के किसी भी स्तर पर, दीर्घकालीन औसत लागत तथा दीर्घकालीन सीमांत लागत $t$ रुपये बढ़ जाती है, रेखाचित्र 4.11 में, दीर्घकालीन सीमांत लागत ‘तथा दीर्घकालीन औसत लागत’ कर लगाने के पश्चात् फर्म की क्रमशः दीर्घकालीन सीमांत लागत वक्र तथा दीर्घकालीन औसत लागत वक्र हैं।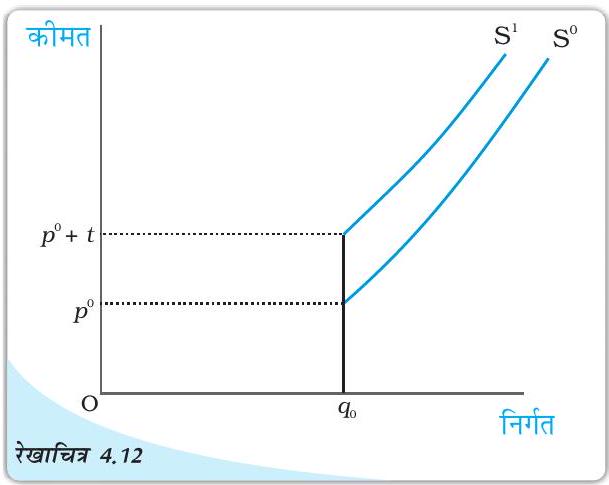

पूर्ति वक्र तथा इकाई कर: इकाई कर के लगने से पूर्व $S^{0}$ एक फर्म का पूर्ति वक्र है। इकाई कर $t$ रुपये लगने के पश्चात्, $\mathrm{S}^{l}$ फर्म के पूर्ति वक्र को दर्शाता है।

याद कीजिए कि फर्म का एक दीर्घकालीन पूर्ति वक्र दीर्घकालीन सीमांत लागत का बढ़ता हुआ भाग है, न्यूनतम दीर्घकालीन औसत लागत से तथा उससे ऊपर जब न्यूनतम दीर्घकालीन औसत लागत से कम सभी कीमतों पर निर्गत शून्य है। रेखाचित्र 4.12 से यह स्पष्ट है कि $s^{0}$ तथा $s^{1}$, क्रमशः इकाई कर लगने के पहले तथा बाद फर्म के दीर्घकालीन पूर्ति वक्र हैं; ध्यान दीजिए कि इकाई कर फर्म के दीर्घकालीन पूर्ति वक्र में बायीं ओर शिफ्ट होता है: किसी भी दी गई बाज़ार कीमत पर अब फर्म निर्गत की कम इकाइयों की पूर्ति करती है।

4.6 बाज़ार पूर्ति वक्र

बाज़ार पूर्ति वक्र वह निर्गत स्तर ( $x$-अक्ष पर अंकित) दर्शाता है जिसका बाज़ार में सभी फर्में समवर्ती विभिन्न बाज़ार मूल्यों ( $y$-अक्ष पर अंकित) पर सामूहिक रूप से उत्पादन करती हैं।

बाज़ार पूर्ति वक्र की किस प्रकार व्युत्पत्ति की जाती है? $n$ फर्मों वाला एक बाज़ार लीजिए: फर्म-1, फर्म- 2 , फर्म-3 तथा इसी प्रकार और भी। मान लीजिए बाज़ार कीमत $p$ पर स्थिर है, तब सामूहिक रूप से $n$ फर्मों द्वारा उत्पादित निर्गत (फर्म-1 की $p$ कीमत पर पूर्ति) + (फर्म-2 की $p$ कीमत पर पूर्ति),$+\ldots . .+$ (कीमत $p$ पर फर्म $n$ द्वारा पूर्ति) है। दूसरे शब्दों में, कीमत $p$ पर बाज़ार पूर्ति व्यक्तिगत फर्मों की दी हुई कीमत पर पूर्तियों का योग है।

आइए अब एक बाज़ार पूर्ति वक्र की ज्यामितीय रचना करें जब बाज़ार में केवल दो फर्में हैं: फर्म-1 तथा फर्म- 2 , दोनों फर्मों की विभिन्न लागत संरचनाएँ हैं। यदि बाज़ार कीमत $\bar{p} _{1}$ से कम है, तो फर्म-1 कुछ भी उत्पादन नहों करेगी और यदि बाज़ार कीमत $\bar{p} _{2}$ से कम है, तो फर्म 2 कुछ भी उत्पादन नहीं करेगी। यह भी मान लीजिए कि $\bar{p} _{2}, \bar{p} _{1}$ से अधिक है।

रेखाचित्र 4.13 की पैनल (a) में हमारे पास फर्म 1 का पूर्ति वक्र है जिसे $S _{1}$ द्वारा दर्शाया गया है; पैनल (b) में हमारे पास फर्म 2 का पूर्ति वक्र है जो $S _{2}$ द्वारा दर्शाया गया है। रेखाचित्र 4.13 की पैनल (c) बाज़ार पूर्ति वक्र दर्शाती है, जो $S _{m}$ द्वारा दर्शाया गया है। जब बाज़ार कीमत $\bar{p} _{1}$ से कम है, तो दोनों फर्में वस्तु की किसी भी मात्रा का उत्पादन नहीं करती हैं। अतः ऐसी सभी कीमत के लिए बाज़ार पूर्ति शून्य होगी। $\bar{p} _{1}$ की तुलना में अधिक अथवा समान बाज़ार कीमत पर परंतु $\bar{p} _{2}$ से कम बाज़ार कीमत पर केवल फर्म- 1 ही वस्तु की किसी सकारात्मक मात्रा का उत्पादन करेगी। अंतः, इस श्रेणी में बाज़ार पूर्ति वक्र, फर्म- 1 के पूर्ति वक्र के संपाती है। $\bar{p} _{2}$ के बराबर अथवा उससे अधिक बाज़ार कीमत पर दोनों फर्मों के पास सकारात्मक निर्गत स्तर होंगे। उदाहरण के लिए, एक ऐसी स्थिति को लेते हैं जहाँ बाज़ार कीमत $p _{3}$ मूल्य ग्रहण कर लेती है (देखिए $p _{3}, \bar{p} _{2}$ से अधिक है)। दी हुई $p _{3}$ पर, फर्म 1 निर्गत की $q _{3}$ इकाइयों की पूर्ति करती है, जबकि फर्म- 2 निर्गत की $q _{4}$ इकाइयों की पूर्ति करती है। अतः कीमत $p _{3}$ पर बाज़ार पूर्ति $q _{5}$ है जहाँ $q _{5}=q _{3}+q _{4}$ । ध्यान दीजिए कि बाज़ार पूर्ति वक्र $S _{m}$ की पैनल (c) में किस प्रकार रचना की गई है : हम बाज़ार की दो फर्मों के पूर्ति वक्रों $S _{1}$ तथा $S _{2}$ के समस्तरीय योग द्वारा $S _{m}$ प्राप्त करते हैं।

ध्यान रखिए कि बाज़ार पूर्ति वक्र, बाज़ार में फर्मों की एक स्थिर संख्या के लिए प्राप्त किया गया है। जैसे-जैसे फर्मों की संख्या में परिवर्तन आता है, बाज़ार पूर्ति वक्र में भी शिफ्ट होता है। विशेष रूप से, यदि बाज़ार में फर्मों की संख्या में वृद्धि (गिरावट) होती है, बाज़ार पूर्ति वक्र में दाहिनी (बायों) ओर शिफ्ट होता है।

अब हम उपर्युक्त ग्राफीय विश्लेषण को संबंधित संख्यात्मक उदाहरण से देखते हैं। दो फर्मों, फर्म-1 तथा फर्म-2 वाले एक बाज़ार को लीजिए। फर्म-1 का पूर्ति वक्र निम्नलिखित है:

$$ S_{1}(p)=\left\{\begin{array}{lr} 0 \qquad : p<10 \\ p-10: p \geq 10 \end{array}\right. $$

ध्यान दीजिए कि $S_{1}(p)$ इंगित करता है कि (1) फर्म- 1,0 निर्गत का उत्पादन करती है यदि बाज़ार कीमत $p, 10$ से स्पष्ट रूप से कम है, तथा (2) फर्म- $1,(p-10)$ निर्गत का उत्पादन करती है यदि बाज़ार कीमत $(p, 10)$ से अधिक अथवा उसके बराबर है।

मान लीजिए, फर्म- 2 का पूर्ति वक्र निम्नवत है:

$$ S_{2}(p)= \begin{cases}0 & : p<15 \\ p-15 & : p \geq 15\end{cases} $$

$S_{2}(p)$ का निर्वचन $S_{1}(p)$ के निर्वचन के समान है। अतः इसे छोड़ दिया गया है। अब बाज़ार पूर्ति वक्र $S_{m}(p)$, सरल रूप से दोनों फर्मों के पूर्ति वक्रों का योग है। दूसरे शब्दों में,

$$ S_{m}(p)=S_{1}(p)+S_{2}(p) $$

परंतु इससे अभिप्राय है कि $S_{m}(p)$ निम्नवत है:

$$ S_{m}(p)= \begin{cases}0 & : p<10 \\ p-10 & : p \geq 10 \text { and } p<15 \\ (p-10)+(p-15)=2 p-25 & : p \geq 15\end{cases} $$

4.7 पूर्ति की कीमत लोच

एक वस्तु की पूर्ति की कीमत लोच, वस्तु की कीमत में परिवर्तनों के कारण वस्तु की पूर्ति की मात्रा की अनुक्रियाशीलता को मापती है। अधिक स्पष्ट रूप में पूर्ति की कीमत लोच जिसे $e_{s}$ से दर्शाया गया है, निम्न प्रकार परिभाषित की जाती है।

पूर्ति की कीमत लोच $\left(e_{s}\right)=\frac{\text { पूर्ति की मात्रा में प्रतिशत परिवर्तन }}{\text { कीमत में प्रतिशत परिवर्तन }}$

$$ =\frac{\frac{\Delta Q}{Q} \times 100}{\frac{\Delta P}{P} \times 100}=\frac{\Delta Q}{Q} \times \frac{P}{\Delta P} $$

जहाँ $\Delta Q$ बाज़ार में आपूर्तित वस्तुओं की मात्रा है, जब बाज़ार में कीमत में $\Delta P$ के बराबर परिवर्तन है।

इसे और अधिक मूर्त बनाने के लिए निम्नलिखित संख्यात्मक उदाहरण पर ध्यान दीजिए। मान लीजिए कि क्रिकेट गेंदों के लिए बाज़ार पूर्ण प्रतिस्पर्धी है। जब एक क्रिकेट गेंद की कीमत 10 रुपये है, मान लीजिए कि बाज़ार फर्मों द्वारा कुल 200 क्रिकेट गेंदों का उत्पादन किया जाता है। जब क्रिकेट गेंदों की कीमत बढ़कर 30 रुपये हो जाती है, मान लीजिए बाज़ार में फर्मों द्वारा कुल 1000 क्रिकेट गेंदों का उत्पादन किया जाता है।

आपूर्तित मात्रा में तथा बाजार मूल्य में प्रतिशत परिवर्तन को निम्न तालिका में दी गई सूचना का उपयोग कर ज्ञात किया जा सकता है:

आपूर्तित मात्रा में प्रतिशत परिवर्तन $=\frac{\Delta Q}{Q_{1}} \times 100$

$$ \begin{aligned} & =\frac{Q_{2}-Q_{1}}{Q_{1}} \times 100 \\ & =\frac{1000-200}{200} \times 100 \\ & =400 \end{aligned} $$

बाज़ार कीमत में प्रतिशत परिवर्तन $=\frac{\Delta P}{P_{1}} \times 100$

$$ \begin{aligned} & =\frac{P_{2}-P_{1}}{P_{1}} \times 100 \\ & =\frac{30-10}{10} \times 100 \\ & =200 \\ & e_{s}=\frac{400}{200}=2 \end{aligned} $$

जब पूर्ति वक्र उध्ध्वस्तरीय है, कीमत के प्रति पूर्ति पूर्ण रूप से असंवेदनशील है तथा पूर्ति की लोच शून्य है। अन्य स्थितियों में जब पूर्ति वक्र सकारात्मक प्रवणता वाली होती है, कीमत में वृद्धि के साथ पूर्ति में भी वृद्धि होती है और इस प्रकार पूर्ति की लोच सकारात्मक होती है। माँग की कीमत लोच के समान, पूर्ति की कीमत लोच भी इकाइयों से स्वतंत्र है।

ज्यामितीय विधि

रेखाचित्र 4.14 को देखें, पैनल $(a)$ एक सीधी रेखा पूर्ति वक्र दर्शाती है। पूर्ति वक्र पर $S$ एक बिंदु है। यह कीमत-अक्ष को इसके धनात्मक भाग पर काटता है तथा जब हम सीधी रेखा को बढ़ाते हैं, यह मात्रा-अक्ष को $M$ बिंदु पर काटता है जो इसके ऋणात्मक भाग

सीधी रेखा पूर्ति वक्रों से संबंधित कीमत लोच का संबंध: पैनल (a) में $\mathrm{S}$ बिंदु पर कीमत लोच $\left(e_{s}\right) 1$ से अधिक है। पैनल (b) में $\mathrm{S}$ पर कीमत लोच (es) 1 के बराबर है। पैनल (c) में $\mathrm{S}$ पर कीमत लोच $\left(e_{\mathrm{s}}\right) 1$ से कम है।

पर है। बिंदु $S$ पर इस पूर्ति वक्र की कीमत लोच, $M q_{0} / O q_{0}$ के अनुपात द्वारा दर्शायी गई है। ऐसे पूर्ति वक्र पर किसी भी बिंदु $S$ के लिए $M q_{0}>O q_{0}$ है। अतः ऐसे पूर्ति वक्र के किसी भी बिंदु पर कीमत लोच 1 से अधिक होगी।

पैनल (c) में हम एक सीधी रेखा पूर्ति वक्र को लेते हैं तथा उस पर $S$ एक बिंदु है। यह मात्रा-अक्ष को $M$ पर काटता है, जो इसके धनात्मक भाग पर है। पुनः इस पूर्ति वक्र के बिंदु $\mathrm{S}$ पर कीमत लोच $M q_{0} / O q_{0}$ के अनुपात से प्राप्त होती है। अब $M q_{0}$ $<O q_{0}$ तथा इस प्रकार $e_{s}<1$ पूर्ति वक्र पर $S$ कोई भी बिंदु हो सकती है तथा इस प्रकार ऐसे पूर्ति वक्र पर सभी बिंदुओं के लिए $e_{s}<1$

अब हम पैनल (b) को देखते हैं। यहाँ पूर्ति वक्र उद्गम बिंदु से होकर जाती है। कोई भी यह सोच सकता है कि यहाँ बिन्दु $M$ तथा उद्गम बिंदु एक ही हैं अर्थात्, $M q_{0}, O q_{0}$ के बराबर हो गया है। बिंदु $S$ पर इस पूर्ति वक्र की कीमत लोच $O q_{0} / O q_{0}$ के अनुपात से प्राप्त होती है जो 1 के बराबर है। उद्गम से होकर जाने वाले सीधी रेखा पूर्ति वक्र के किसी भी बिंदु पर कीमत लोच 1 होगी।

4.8 सारांश

• एक पूर्ण प्रतिस्पर्धी बाज़ार में फर्म कीमत-स्वीकारक होती हैं।
• फर्म की कुल संप्राप्ति, फर्म की कुल निर्गत बाज़ार कीमत का गुणनफल होती है।
• कीमत-स्वीकारक फर्म की औसत संप्राप्ति बाज़ार कीमत के बराबर होती है।
• कीमत-स्वीकारक फर्म के लिए सीमांत संप्राप्ति बाज़ार कीमत के बराबर होती है।
• पूर्ण प्रतिस्पर्ीी बाज़ार में फर्म का माँग वक्र पूर्णतः लोचचदार होती है। यह बाज़ार कीमत पर एक सीधी समस्तरीय सीधी रेखा होती है।
• फर्म का लाभ, कुल संप्राप्ति जो वह अर्जित करती है तथा कुल लागत जो वह उठाती है, इनके बीच का अंतर होता है।
• यदि अल्पकाल में किसी फर्म के लाभ का अधिकतमीकरण निर्गत के किसी धनात्मक स्तर पर होता है, तो उस निर्गत स्तर पर तीन शर्ते पूरी होनी चाहिए:

(i) $p=$ अल्पकालीन सीमांत लागत

(ii) अल्पकालीन सीमांत लागत घट नहीं रही है।

(iii) $p \geq$ औसत परिवर्ती लागत

• यदि दीर्घकाल में किसी फर्म के लाभों का अधिकतमीकरण निर्गत के किसी सकारात्मक स्तर पर होता है, तो उस निर्गत पर तीन शर्ते पूरी होनी चाहिए:

(i) $p=$ दीर्घकालीन सीमांत लागत

(ii) दीर्घकालीन सीमांत लागत घट नही रही है।

(iii) $p \geq$ दीर्घकालीन औसत लागत

• किसी फर्म अल्पकालीन पूर्ति वक्र, अल्पकालीन सीमांत लागत वक्र का न्यूनतम औसत परिवर्ती लागत तथा उससे ऊपर उठता हुआ भाग होता है तथा न्यूनतम औसत परिवर्ती लागत से कम सभी कीमतों पर निर्गत स्तर शुन्य होता है।
• किसी फर्म का दीर्घकालीन पूर्ति वक्र, दीर्घकालीन सीमांत लागत वक्र का न्यूनतम दीर्घकालीन सीमांत लागत तथा उससे ऊपर, उठता हुआ भाग होता है तथा न्यूनतम दीर्घकालीन सीमांत लागत से कम, सभी कीमतों पर निर्गत स्तर शून्य होता है।
• प्रौद्योगिकीय प्रगति से फर्म का पूर्ति वक्र दाहिनी ओर शिफ्ट हो जाती है।
• आगतों की कीमतों में वृद्धि (कमी) से फर्म का पूर्ति वक्र बायों (दाहिनी) ओर शिफ्ट हो जाती है।
• प्रति इकाई कर लगाने से फर्म का पूर्ति वक्र बायों ओर शिफ्ट हो जाती है।
• बाज़ार पूर्ति वक्र सभी व्यक्तिगत फर्मों के पूर्ति वक्रों के समस्तरीय योग द्वारा प्राप्त होता है।
• वस्तु की पूर्ति की कीमत लोच वस्तु की बाज़ार कीमत में एक प्रतिशत परिवर्तन के फलस्वरूप पूर्ति की गई मात्रा में प्रतिशत परिवर्तन है।

4.9 मूल संकल्पनाएँ

4.10 अभ्यास

1. एक पूर्ण प्रतिस्पर्धी बाज़ार की क्या विशेषताएँ हैं?

2. एक फर्म की संप्राप्ति, बाज़ार कीमत तथा उसके द्वारा बेची गई मात्रा में क्या संबंध है?

3. कीमत रेखा क्या है?

4. एक कीमत-स्वीकारक फर्म का कुल संप्राप्ति वक्र, ऊपर की ओर प्रवणता वाली सीधी रेखा क्यों होती है? यह वक्र उद्गम से होकर क्यों गुजरती है?

5. एक कीमत-स्वीकारक फर्म का बाज़ार कीमत तथा औसत संप्राप्ति में क्या संबंध है?

6. एक कीमत-स्वीकारक फर्म की बाज़ार कीमत तथा सीमांत संप्राप्ति में क्या संबंध है?

7. एक पूर्ण प्रतिस्पर्धी बाज़ार में लाभ-अधिकतमीकरण फर्म की सकारात्मक उत्पादन करने की क्या शर्तें हैं?

8. क्या प्रतिस्पर्धी बाज़ार में लाभ-अधिकतमीकरण फर्म जिसकी बाज़ार कीमत सीमांत लागत के बराबर नहीं है, उसका निर्गत का स्तर सकारात्मक हो सकता है। व्याख्या कीजिए।

9. क्या एक प्रतिस्पर्धी बाज़ार में कोई लाभ-अधिकतमीकरण फर्म सकारात्मक निर्गत स्तर पर उत्पादन कर सकती है, जब सीमांत लागत घट रही हो। व्याख्या कीजिए।

10. क्या अल्पकाल में प्रतिस्पर्धी बाज़ार में लाभ-अधिकतमीकरण फर्म सकारात्मक स्तर पर उत्पादन कर सकती है, यदि बाज़ार कीमत न्यूनतम औसत परिवर्ती लागत से कम है। व्याख्या कीजिए।

11. क्या दीर्घकाल में स्पर्धी बाज़ार में लाभ-अधिकतमीकरण फर्म सकारात्मक स्तर पर उत्पादन कर सकती है? यदि बाज़ार कीमत न्यूनतम औसत लागत से कम है, व्याख्या कीजिए।

12. अल्पकाल में एक फर्म का पूर्ति वक्र क्या होती है?

13. दीर्घकाल में एक फर्म का पूर्ति वक्र क्या होती है?

14. प्रौद्योगिकीय प्रगति एक फर्म के पूर्ति वक्र को किस प्रकार प्रभावित करती है?

15. इकाई कर लगाने से एक फर्म के पूर्ति वक्र को किस प्रकार प्रभावित करता है?

16. किसी आगत की कीमत में वृद्धि एक फर्म के पूर्ति वक्र को किस प्रकार प्रभावित करती है?

17. बाज़ार में फर्मों की संख्या में वृद्धि, बाज़ार पूर्ति वक्र को किस प्रकार प्रभावित करती है?

18. पूर्ति की कीमत लोच का क्या अर्थ है? हम इसे कैसे मापते हैं?

19. निम्न तालिका में कुल संप्राप्ति, सीमांत संप्राप्ति तथा औसत संप्राप्ति का परिकलन कीजिए। वस्तु की प्रति इकाई बाज़ार कीमत 10 रुपये है।

20. निम्न तालिका में एक प्रतिस्पर्धी फर्म की कुल संप्राप्ति तथा कुल लागत सारणियों को दर्शाया गया है। प्रत्येक उत्पादन स्तर वे लाभ की गणना कीजिए। वस्तु की बाज़ार कीमत भी निर्धरित कीजिए।

21. निम्न तालिका में एक प्रतिस्पर्धी फर्म की कुल लागत सारणी को दर्शाया गया है। वस्तु की कीमत 10 रु० दी हुई है। प्रत्येक उत्पादन स्तर पर लाभ की गणना कीजिए। लाभ-अधिकतमीकरण निर्गत स्तर ज्ञात कीजिए।

22. दो फर्मों वाले एक बाज़ार को लीजिए। निम्न तालिका दोनों फर्मों के पूर्ति सारणियों को दर्शाती है: $\mathrm{SS}{1}$ कालम में फर्म- 1 की पूर्ति सारणी, कालम $\mathrm{SS}{2}$ में फर्म-2 की पूर्ति सारणी है। बाज़ार पूर्ति सारणी का परिकलन कीजिए।

23. एक दो फर्मों वाले बाज़ार को लीजिए। निम्न तालिका में कालम $\mathrm{SS}{1}$ तथा कालम $\mathrm{SS}{2}$, क्रमशः फर्म-1 तथा फर्म-2 के पूर्ति सारणियों को दर्शाते हैं। बाज़ार पूर्ति सारणी का परिकलन कीजिए।

24. एक बाज़ार में 3 समरूपी फर्म हैं। निम्न तालिका फर्म-1 की पूर्ति सारणी दर्शाती है। बाज़ार पूर्ति सारणी का परिकलन कीजिए।

25. 10 रु० प्रति इकाई बाज़ार कीमत पर एक फर्म की संप्राप्ति 50 रुपये है। बाज़ार कीमत बढ़कर 15 रु० हो जाती है और अब फर्म को 150 रु० की संप्राप्ति होती है। पूर्ति वक्र की कीमत लोच क्या है?

26. एक वस्तु की बाज़ार कीमत 5 रु० से बदलकर 20 रु० हो जाती है। फलस्वरूप फर्म पूर्ति की मात्रा 15 इकाई बढ़ जाती है। फर्म के पूर्ति वक्र की कीमत लोच 0.5 है। फर्म का आरंभिक तथा अंतिम निर्गत स्तर ज्ञात करें।

27. 10 रु० बाज़ार कीमत पर एक फर्म निर्गत की 4 इकाइयों की पूर्ति करती है। बाज़ार कीमत बढ़कर 30 रु० हो जाती है। फर्म की पूर्ति की कीमत लोच 1.25 है। नई कीमत पर फर्म कितनी मात्रा की पूर्ति करेगी?