पूर्व अध्याय में हमने उपभोक्ता के व्यवहार के संबंध में चर्चा की है। इस अध्याय तथा अगले अध्याय में हम उत्पादक के व्यवहार की जाँच करेंगे। एक उत्पादक अथवा फर्म विभिन्न आगतों जैसे- श्रम, मशीन, भूमि, कच्चा माल आदि को प्राप्त करता है। इन आगतों के मेल से वह निर्गत का उत्पादन करता है। उत्पादन वह प्रकिया है जिसके द्वारा आगतों को ‘निर्गत’ में परिवर्तित किया जाता है। उत्पादन, उत्पाद का अथवा फर्मो द्वारा किया जाता है। एक फर्म विभिन्न आगतों जैसे मशीनें, भूमि, कच्चा माल आदि को कम करती है। वह इन आगतों को ‘निर्गत’ उत्पन्न करने में उपयोग करती है। यह निर्गत उपभोगताओं द्वारा उपयोग किया जा सकता है, अथवा अन्य फर्मों द्वारा और आगे उत्पादन करने के लिये उपयोग किया जा सकता है। उदाहरणार्थ, एक दर्जी एक सिलाई मशीन, कपड़ा धागा और अपने स्वंय के श्रम को कमीजें बनाने के लिए उपयोग करता है। एक कृषक अपनी भूमि, श्रम, ट्रैक्टर, बीज, खाद, पानी आदि को गेंहू उत्पन्न करने में उपयोग करता है। एक कार निर्माता भूमि का फैक्टरी के लिये उपयोग करता है तथा मशीनों, श्रम और दूसरे विभिन्न आगतों (स्टील, एल्यूमीनियम, रबर आदि) का कारों के उत्पादक के लिये। एक रिक्शाचालक रिक्शे और स्वयं के श्रम का उपयोग करता है। एक घरेलू सहायक अपने श्रम का उपयोग सफाई सेवाएं उत्पन्न करने मे करता है।

प्रारम्भ करने के लिये हम कुछ सरल मान्यताएँ लेकर चलते हैं। उत्पादन तात्कालिक है: अपने सरल उत्पादन-मॉडल में, आगतों के संयोगों और निर्गतों के उत्पादन में कोई समय नहीं बीतता। हम ‘उत्पादन’ एवं ‘पूर्ति’ शब्दों को समानार्थी तथा बहुधा अंतर्परिवर्तनीय मानकर उपयोग करते हैं।

आगतों को प्राप्त करने के लिये एक फर्म को उनके लिए कुछ देना पड़ता है। इसे उत्पादन लागत कहते हैं। एक बार जब ‘निर्गत’ उत्पन्न हो जाता है, फर्म उसे बाज़ार में बेच देती है और ‘आगम’ प्राप्त करती है। ‘आगम’ तथा ‘लागत’ के बीच अन्तर को ‘फर्म का लाभ’ कहते है। हम यह मानते हैं कि एक फर्म का उद्देश्य अधिकतम लाभ, जितना वह कर सके, प्राप्त करना है।

इस अध्याय में, हम आगतों तथा निर्गतों के बीच संबंध की चर्चा करेगें। हम फर्म के लागत ढाँचे पर विचार करेगें हम ऐसा इस लिये करते हैं, ताकि हमें उस उत्पादन को ज्ञात कर सकें जिस पर फर्मों के लाभ अधिकतम होते हैं।

3.1 उत्पादन फलन

एक फर्म का उत्पादन फलन उपयोग में लाए गए आगतों तथा फर्म द्वारा उत्पादित निर्गतों के मध्य का संबंध है। उपयोग में लाए गए आगतों की विभिन्न मात्राओं के लिए यह निर्गत की अधिकतम मात्रा प्रदान कर सकता है, जिसका उत्पादन किया जा सकता है।

उस कृषक के बारे में विचार कीजिये जिसका हमने ऊपर जिक्र किया है। सरलता के लिए हम यह मान लेते हैं कि एक कृषक गेहूँ का उत्पादन करने के लिए केवल दो निर्गतो - भूमि तथा श्रम का उपयोग करता है। एक उत्पादन फलन हमें गेहूँ की उस अधिकतम मात्रा को बताता है जिसे वह दी गई भूमि की मात्रा का उपयोग तथा दिये गये श्रम घंटों में काम कर उत्पन्न कर सकता है। मान लीजिये वह अधिकतम दो टन गेहूँ उत्पन्न करने के लिए एक दिन में 2 घंटे काम करता है और एक हेक्टेयर भूमि का उपयोग करता है। अतः वह फलन जो इस संबंध को व्यक्त करता है, उत्पादन फलन कहलाता है।

इस संबंध के रूप का एक संभव उदाहरण यह हो सकता है:

$\mathrm{q}=\mathrm{K}\times \mathrm{L}$

यहाँ $\mathrm{q}$ उत्पन्न गेहूँ की मात्रा है, $\mathrm{K}$ हेक्टेयरो में भूमि का क्षेत्रफल है, $\mathrm{L}$ एक दिन में किये गए काम के घंटे हैं।

उत्पादन फलन का इस प्रकार वर्णन, हमें आगतों एवं निर्गतों के मध्य सही संबंध को बतलाता है। यदि $\mathrm{K}$ अथवा $\mathrm{L}$ किसी में भी वृद्धि होती है, तो $\mathrm{q}$ में भी वृद्धि होगी। किसी भी $\mathrm{K}$ के लिये केवल एक $\mathrm{q}$ होगा। परिभाषानुसार, हम निर्गतों के किसी भी स्तर पर, अधिकतम आगत को लेते हैं, एक उत्पादन फलन आगतों के कुशल उपयोग का अध्ययन करता है। कुशलता से यहाँ अभिप्राय है कि निर्गतों के उसी स्तर से और अधिक उत्पादन सम्भव नहीं हैं।

एक उत्पादन फलन, एक दी हुई प्रौद्योगिकों के लिए परिभाषित किया जाता है। यह प्रौद्योगिकीय ज्ञान है जो निर्गत के अधिकतम स्तरों को निर्धारित करता है, जिसका उत्पादन आगतों के विभिन्न संयोगों को उपयोग में लाकर किया जा सकता है। यदि प्रौद्योगिकी में सुधार होता है, तो विभिन्न आगत संयोगों में वृद्धि से प्राप्त होने वाले निर्गत के अधिकतम स्तरों को प्राप्त की जा सकती है। तब हमें एक नवीन उत्पादन फलन प्राप्त होता है।

उत्पदान प्रक्रिया में फर्म जिन आगतों का उपयोग करती है, वे उत्पादन का कारक कहलाते हैं। अपने अपने निर्गत के उत्पादन के क्रम में एक फर्म कितने ही विभिन्न आगतों का प्रयोग कर सकती है। इस समय हम एक ऐसी फर्म पर विचार करेंगे, जो केवल उत्पादन के 2 कारकों- श्रम एवं पूंजी। हमारा उत्पादन फलन, इसलिये, हमें उस अधिकतम उत्पादन की मात्रा (q) को बतलाता है

तालिका 3.1: उत्पादन फलन

जो इन दो उत्पादन के कारकों के श्रम (L)और पूँजी (K) के विभिन्न संयोगों के उपयोग करने से प्राप्त किया जा सकता है।

हम उत्पादन फलन को प्रकार व्यक्त कर सकते हैं:-

$$\begin{array}{}\text{(3.1)}& \mathrm{q}=f(\mathrm{L},\mathrm{K})\end{array}$$

जहाँ $\mathrm{L}$ श्रम है और $\mathrm{K}$ पूंजी है और $\mathrm{q}$ वह अधिकतम उत्पादन है जो उत्पन्न किया जा सकता है।

तालिका 3.1 में उत्पादन फलन का एक संख्यात्मक उदाहरण दिया गया है। बायाँ कॉलम श्रम की मात्रा दर्शाता है तथा ऊपर की पंक्ति पूंजी की मात्रा दर्शाती है। जैसे-जैसे हम किसी भी पंक्ति में दायीं तरफ जाते हैं, पूंजी में वृद्धि होती है तथा जैसे-जैसे हम किसी भी कॉलम में नीचे की तरफ जाते हैं तो श्रम में वृद्धि होती है। दोनों कारकों के विभिन्न मानों के लिए, तालिका तदुनुरूप निर्गत स्तर दर्शाती है। उदाहरण के तौर पर, श्रम की 1 इकाई तथा पूंजी की 1 इकाई के साथ फर्म अधिक से अधिक निर्गत की 1 इकाई, श्रम की 2 इकाई तथा पूंजी की 2 इकाई के साथ यह निर्गत की 10 इकाई का, श्रम की 3 इकाई तथा पूंजी की 2 इकाई के साथ अधिक से अधिक निर्गत की 18 इकाई तथा इसी तरह से आगे भी उत्पादन किया जाता है।

हमारे उदाहरण में उत्पादन के लिए दोनों आगत आवश्यक है। यदि कोई भी आगत शून्य हो जाता है, तो कोई भी उत्पादन नहीं होगा। दोनों सकारात्मक आगतों के साथ, निर्गत सकारात्मक होगा। जैसे-जैसे हम किसी आगत की मात्रा में वृद्धि करते जाते हैं, निर्गत में वृद्धि होती जाती है।

समान मात्रा

अध्याय 2 में हमने अनधिमान वक्र के विषय में जाना। यहाँ हमने इसी प्रकार की एक संकल्पना जिसे समान मात्रा कहा जाता है, का परिचय कराया है। यह केवल उत्पादन फलन का प्रतिनिधित्व करने का एक वैकल्पिक उपाय है। दो आगतों- कारक 1 तथा कारक 2 वाले एक उत्पादन फलन पर विचार कीजिए। एक समान मात्रा उन दो आगतों के संमाक संयोगों का सेट होता है, जोकि समान अधिकतम संभावित स्तर का निर्गत प्राप्त करता है। प्रत्येक समान मात्रा निर्गत के एक विशेष स्तर का प्रतिनिधित्व करती है तथा निर्गत की मात्रा को स्तर प्रदान करती है।

तालिका 3.1 को पुन: देखे। स्पष्ट है कि 10 इकाई उत्पादन तीन प्रकार प्राप्त किया जा सकता है $(4\mathrm{L},1\mathrm{K}),(2\mathrm{L},2\mathrm{K}),(1\mathrm{L},4\mathrm{K})$ । $\mathrm{L}$ तथा $\mathrm{K}$ के समस्त संयोग, एक ही समोत्पाद वक्र स्थित हैं जो निर्गत स्तर 10 को दिखाता है। क्या आप आगतों के उन सभी संयोगो की पहचान कर सकते हैं जो समोत्वाद रेखा $\mathrm{q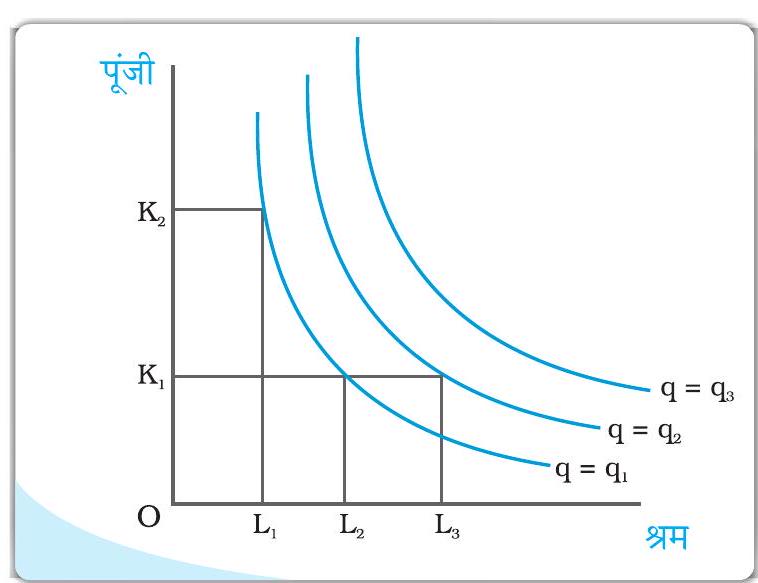}=50$ पर स्थित होंगे?

दिया गया चित्र इस संकल्पना का सामान्यीकरण करता है। हम $\mathrm{L}$ को $\mathrm{X}$ अक्ष पर और $\mathrm{K}$ को $\mathrm{Y}$ अक्ष पर दिखाते हैं। हमारे पास आगत समतल में तीन निर्गत स्तरों के लिए तीन समान मात्रा हैं- $q=q_1,q_{=}=q_2$, तथा $\mathrm{q}={\mathrm{q}}_3$ । दो आगत संयोग $({\mathrm{L}}_1,{\mathrm{K}}_2)$ तथा $({\mathrm{L}}_2,{\mathrm{K}}_1)$ हमें निर्गत ${\mathrm{q}}_1$ का समान स्तर देते हैं। यदि हम पूंजी को ${\mathrm{K}}_1$ पर स्थिर करें तथा श्रम को ${\mathrm{L}}_3$ तक बढ़ा दें, तो निर्गत में वृद्धि होती है तथा हम एक और ऊँचे समान मात्रा $\mathrm{q}={\mathrm{q}}_2$ पर पहुँच जाते हैं। जब सीमांत उत्पाद एक आगत की अधिक मात्रा से सकारात्मक होते हैं, समान स्तर के निर्गत का उत्पादन अन्य आगत की कम मात्रा उपयोग में लाकर हो सकती है। अतः समान मात्रा नकारात्मक प्रवणता वाले होते हैं।

3.2 अल्पकाल तथा दीर्घकाल

इससे पूर्व कि हम कोई अन्य विश्लेषण आरंभ करें, दो संकल्पनाएँ: अल्पकाल तथा दीर्घकाल का यहाँ चर्चा करना महत्त्वपूर्ण है।

अल्पकाल में कम से कम एक कारक, श्रम अथवा पूँजी में परितर्वन नहों किया जा सकता अतः वह स्थिर रहता है। निर्गत स्तर में परिवर्तन लाने के लिये, फर्म केवल दूसरे कारक में ही परिवर्तन कर सकती है। जो कारक स्थिर कारक कहलाता है जबकि दूसरा कारक जिसमें फर्म परिवर्तन कर सकती है, परिवर्ती कारक कहलाता है।

तालिका 3.1 में दर्शाए गए उदाहरण पर गौर कीजिए। मान लीजिए कि अल्पकाल में 4 इकाइयों पर पूंजी स्थिर रहता है। तब तद्नुरूप कॉलम निर्गत के विभिन्न स्तर दर्शाता है, जिनका फर्म उत्पादन अल्पकाल में श्रम की विभिन्न मात्राएँ उपयोग में लाकर कर सकती हैं।

दीर्घकाल में उत्पादन के सभी कारकों में परिवर्तन लाया जा सकता है। एक फर्म निर्गत के विभिन्न स्तरों का उत्पादन करने के लिए, दीर्घकाल में दोनों कारकों में साथ-साथ परिवर्तन ला सकती है। अतः दीर्घकाल में कोई भी स्थिर कारक नहीं है।

किसी भी विशेष उत्पादन प्रक्रम में दीर्घकाल साधारणतः अल्पकाल की तुलना में एक दीर्घ समय अंतराल को प्रकट करता है। विभिन्न उत्पादन प्रक्रमों के लिए दीर्घकाल कालावधि भिन्न हो सकती है। अल्पकाल तथा दीर्घकाल को दिनों, महीनों अथवा वर्षों के रूप में परिभाषित करना उचित नहीं है। हम दीर्घावधि तथा अल्पावधि को सामान्यतः इस दृष्टि को ध्यान में रखकर परिभाषित करते हैं कि सभी आगत परिवर्ती हैं अथवा नहीं।

3.3 कुल उत्पाद, औसत उत्पाद तथा सीमांत उत्पाद

3.3.1 कुल उत्पाद

मान लीजिये, हम एक आगत में परिवर्तन लाते हैं तथा अन्य आगतों को स्थिर रखते हैं। तब उस आगत के विभिन्न स्तरों से, हम निर्गत के विभिन्न स्तर प्राप्त करते हैं। परिवर्ती आगत तथा परिवर्ती निर्गत के मध्य संबंध को, अन्य सभी आगतों को स्थिर से रखते हुए, अक्सर परिवर्ती आगत के कुल उत्पाद $\mathrm{TP}$ के रूप में जाना जाता है।

तालिका 3.1 को पुन: देखें। मान लीजिये पूँजी, 4 इकाई पर निश्चित की जाती है। अब तालिका 3.1 में, उस कॉलम को देखें जहाँ पूँजी दिखाई गई है। जब हम कालम के नीचे की ओर जाते हैं, तो हम कारक श्रम के विभिन्न मूल्यों के लिये, निर्गत मूल्य प्राप्त करते हैं। यह कारक श्रम का कुल उत्पाद है जिसकी मान ${\mathrm{K}}_2=4$ है। इसे कभी-कभी कुल प्रतिफल (Total Return) अथवा परिवर्ती आगतों का कुल भौतिक उत्पाद (Total Physical Product) भी का जाता है। इसे तालिका 3.2 के द्वितीय कॉलम में पुनः दिखाया गया है।

एक बार जब हमने कुल उत्पाद को परिभाषित कर दिया, तो औसत उत्पाद तथा सीमांत उत्पाद की संकल्पना को परिभाषित करना उपयोगी होगा। उत्पादन प्रक्रिया में परिवर्ती आगतों के योगदान की व्याख्या करने के लिए ये उपयोगी हैं।

3.3.2 औसत उत्पाद

औसत उत्पाद निर्गत की प्रति इकाई परिवर्ती आगत के रूप में परिभाषित किया जाता है। हम इसकी गणना इस प्रकार करते हैं:

$$\begin{array}{}\text{(3.3)}& A{P}_L=\frac{T{P}_L}{L}\end{array}$$

तालिका 3.2 का अंतिम कॉलम श्रम की औसत उत्पाद (पूँजी 4 इकाइयों पर स्थिर रखकर) तालिका 3.1 में वर्णित उत्पादन फलन का एक संख्यात्मक उदाहरण है। इस कॉलम के मूल्यों को $\mathrm{TP}$ (कॉलम 2) को $\mathrm{L}$ से विभाजित करके (कॉलम 1) प्राप्त किया गया है।

3.3.3 सीमांत उत्पाद

एक आगत का सीमांत उत्पाद, प्रति इकाई आगत में परिवर्तन के कारण जो निर्गत में परिवर्तन होता है, जब सभी अन्य आगत स्थिर रखे गये हों, कहा जाता है।

जब पूँजी को स्थिर रखा जाता है, तो श्रम का सीमांत उत्पाद होता है-

$$\begin{array}{rl}\text{ सीमांत उत्पाद }& =\frac{\text{ निर्गत में परिवर्तन }}{\text{ आगत में परिवर्तन }}\\ \text{(3.4)}& & =\frac{\mathrm{\Delta }T{P}_L}{\mathrm{\Delta }L}\end{array}$$

जहाँ $\mathrm{\Delta }$ परिवर्त में परिवर्तन का सूचक है।

तालिका 3.2 का अंतिम कॉलम, श्रम की सीमान्त उत्पाद (पूँजी 4 इकाइयों पर स्थिर रख कर) तालिका 3.1 में वर्णित उत्पादन फलन का एक संख्यात्मक उदाहरण है। इस कॉलम के मूल्यों को $\mathrm{TP}$ में परिवर्तन को $\mathrm{L}$ में परिवर्तन से विभाजित करके प्राप्त किया गया है। उदाहरणार्थ, जब $\mathrm{L}$, 1 से 2 में परिवर्तित होता है जो $\mathrm{TP},10$ से 24 हो जाती है।

$$\begin{array}{}\text{(3.5)}& {\mathrm{MP}}_{\mathrm{L}}=(\mathrm{L}\text{ इकाइयों पर }\mathrm{TP})-(\mathrm{L}-1\text{ इकाई पर }\mathrm{TP})\end{array}$$

यहाँ $\mathrm{TP}$ में परिवर्तन $=24=(10=14)$

$\mathrm{L}$ में परिवर्तन $=1$

श्रम की दूसरी इकाई की सीमान्त उत्पाद $14/1=14$

तालिका 3.2: कुल उत्पाद, सीमांत उत्पाद तथा औसत उत्पाद

क्योंकि निर्गतों के मूल्य ऋणात्मक नहीं हो सकते, सीमांत उत्पाद पर आगत प्रयोग के शून्य स्तर अपरिभाज़ित रहता है। आगतों के किसी भी स्तर पर एक आगत का औसत उत्पाद उस स्तर तक सभी सीमान्त उत्पादों का औसत होता है। इस प्रकार कुल उत्पाद, सीमान्त उत्पादों का योग होता है।

प्रयोग के किसी भी स्तर पर एक आगत का औसत उत्पाद उस स्तर तक सभी सीमांत उत्पादों का औसत होता है। औसत तथा सीमांत उत्पाद अक्सर औसत तथा सीमांत प्रतिफल के रूप में क्रमशः परिवर्ती आगतों के लिए जाने जाते हैं।

3.4 ह्रासमान सीमांत उत्पाद नियम तथा परिवर्ती अनुपात नियम

श्रम को $\mathrm{X}$ अक्ष पर तथा निर्गत को $\mathrm{Y}$ अक्ष पर रख कर, यदि हम तालिका 3.2 को ग्राफ पर चित्रित करें, तो हमें चित्र में प्रदर्शित वक्र प्राप्त होते हैं। आइये देखते हैं कि $\mathrm{TP}$ का क्या हो रहा है? देखिये, श्रम आगत में वृद्धि के साथ TP बढ़ती है परन्तु जिस दर से यह बढ़ती है वह समान नहीं है। श्रम में 1 से 2 वृद्धि होने पर, TP में 10 की वृद्धि होती है। श्रम में 2 से 3 वृद्धि होने पर, TP में 12 की वृद्धि होती है।

TP में वृद्धि की दर MP द्वारा दिखाई गई है। देखिये, MP पहले बढ़ती है ( श्रम की 3 इकाइयों तक) और फिर गिरनी शुरू करती है। MP की इस प्रवृत्ति को यह पहले बढ़ती है, तथा फिर गिरती है, परिवर्तनीय अनुपातों का नियम है अथवा समान सीमान्त उत्पाद का नियम कहा जाता है। परिवर्ती उत्पादों का नियम बताता है कि एक आगत कारक का सीमान्त उत्पाद प्रारंभ में बढ़ता है और एक निश्चित रोजगार के स्तर पर पहुंचकर, गिरने लगता है।

ऐसे क्यों होता है? इसको समझने के लिये पहले हम कारक अनुपातों की संकल्पना को परिभाषित करते हैं। कारक अनुपात, उस अनुपात को बतलाता है जिसमें निर्गत उत्पन्न करने के लिये दो कारको को संयोजित किया जाता हैं।

जैसे हम एक कारक आगत को स्थिर रखते हैं तथा दूसरे में निरंतर वृद्धि करते हैं, तो कारक अनुपातों में परिवर्तन आ जाता है। प्रारंभ में, जैसे-जैसे हम परिवर्ती आगत की मात्रा में वृद्धि करते हैं, कारक अनुपात उत्पादन के लिए अधिकाधिक उपयुक्त होता जाता है तथा सीमांत उत्पाद में वृद्धि हो जाती है। परंतु प्रयोगकर्ता के एक विशेष स्तर के पश्चात् उत्पादन प्रक्रम परिवर्ती आगत के साथ अत्यंत अस्त-व्यस्त हो जाता है।

मान लीजिये तालिका 3.2 उस कृषक के निर्गत को दिखाती है जिसके पास 4 हेक्टेयर भूमि है, और वह यह तय कर सकता है कि वह कितना श्रम उपयोग करे, तो श्रमिक के पास अकेले ही जोतने के लिये अत्यधिक भूमि है। जैसे-जैसे वह श्रमिकों की संख्या में वृद्धि करता है, प्रति इकाई भूमि, श्रम की मात्रा बढ़ जाती है और प्रत्येक श्रमिक कुल निगति में अनुपात से अधिक वृद्धि करता है। इस स्थिति में सीमांत उत्पाद बढ़ जाता है जब चौथे श्रमिक को लगाया जाता है, तो भूमि पर भीड़ हो जाती है। प्रत्येक श्रमिक के पास कुशलता पूर्वक काम करने के लिये अपर्याप्त भूमि होती है। अतः प्रत्येक श्रमिक द्वारा उत्पादन में वृद्धि अनुपातन कम होती है। सीमांत उत्पाद में होना शुरू हो जाती है।

हम इन प्रेक्षणों को नीचे दिये अनुसार TP, MP तथा AP वक्रों को संभालने के लिये उपयोग कर सकते हैं।

3.5 कुल उत्पाद, सीमांत उत्पाद तथा औसत उत्पाद वक्र की आकृतियाँ

अन्य आगतों को स्थिर रखते हुए एक आगत की मात्रा में वृद्धि के परिणामस्वरूप सामान्यतः निर्गत में वृद्धि होती है। तालिका 3.2 दर्शाती है कि किस प्रकार कुल उत्पाद में परिवर्तन आता है, जैसे-जैसे श्रम की मात्रा में वृद्धि होती है। आगत-निर्गत समतल में कुल उत्पाद वक्र हर स्थिति में धनात्मक प्रवणता वाला वक्र होता है। रेखाचित्र 3.1 एक विशिष्ट फर्म के लिए कुल उत्पाद वक्र का आकार दर्शाती है।

कुल उत्पादः यह श्रम के लिए कुल उत्पाद वक्र है। जब अन्य सभी आगत स्थिर रखे जाते हैं, श्रम विभिन्न मात्राओं से प्राप्त किए जाने वाले विभिन्न निर्गत स्तरों को दर्शाता है।

हम श्रम की इकाइयाँ समस्तरीय अक्ष पर तथा निर्गत ऊर्र्वस्तर अक्ष पर मापते हैं। श्रम की $\mathrm{L}$ इकाइयों के साथ फर्म निर्गत की $q_1$ इकाइयों का अधिक-से-अधिक उत्पादन कर सकती है।

परिवर्ती अनुपात के नियम के अनुसार, एक आगत के सीमांत उत्पाद में आरंभ में वृद्धि होती है, इसके पश्चात् प्रयोग के एक विशेष स्तर पर पहुँचकर इसमें गिरावट प्रारंभ हो जाती है। अतः आगत निर्गत समतल में सीमांत उत्पाद वक्र दिखता है, एक उल्टे ’ $U$ ’ वक्र आकृति के रूप में। आइए, अब हम देखते हैं औसत उत्पाद वक्र कैसा दिखता है? परिवर्ती आगत की पहली इकाई के लिए कोई सरलता से जाँच सकता है कि सीमांत उत्पाद तथा औसत उत्पाद समान होते हैं। अब, जैसे-जैसे हम आगत की मात्रा में वृद्धि करते जाते हैं, सीमांत उत्पाद में वृद्धि होती जाती है। सीमांत उत्पादों के औसत होने के कारण औसत उत्पाद में भी वृद्धि होती है, परंतु सीमांत उत्पाद की तुलना में कम वृद्धि होती है। तब एक बिंदु के पश्चात् सीमांत उत्पाद में गिरावट आनी आरंभ हो जाती है। जब तक सीमांत उत्पाद का मूल्य प्रचलित औसत उत्पाद के मूल्य की तुलना में अधिक रहता है, औसत उत्पाद में वृद्धि होती रहती है। एक बार सीमांत उत्पाद में पर्याप्त रूप से गिरावट आ जाने पर, इसका मूल्य प्रचलित औसत उत्पाद की तुलना में कम हो जाता है और बाद में भी औसत उत्पाद में गिरावट आरंभ हो जाती है। अतः, औसत उत्पाद वक्र भी उल्टे ’ $U$ ’ की आकृति का होता है।

जब तक औसत उत्पाद में वृद्धि होती रहती है, इस स्थिति में सीमांत उत्पाद, औसत उत्पाद की तुलना में अधिक होता है। अन्यथा, औसत उत्पाद में वृद्धि नहीं हो सकती है। समान रूप से, जब औसत उत्पाद में गिरावट आती है, सीमांत उत्पाद को औसत उत्पाद की तुलना में आवश्यक रूप से कम होना चाहिए। इससे यह निष्कर्ष निकलता है कि सीमांत उत्पाद वक्र औसत उत्पाद वक्र को अधिकतम औसत उत्पाद के बिंदु से ऊपर से काटता है।

औसत तथा सीमांत उत्पादः यह श्रम का औसत तथा सीमांत उत्पाद वक्र है।

रेखाचित्र 3.2 एक विशिष्ट फर्म के औसत उत्पाद तथा सीमांत उत्पाद वक्रों की आकृति को दर्शाता है।

श्रम का औसत उत्पाद $L$ पर अधिकतम है। $L$ के बाईं ओर औसत उत्पाद में वृद्धि हो रही है तथा सीमांत उत्पाद, औसत उत्पाद की तुलना में अधिक है। $L$ के दाहिनी ओर औसत उत्पाद में गिरावट आ रही है तथा सीमांत उत्पाद, औसत उत्पाद की तुलना में कम है।

3.6 पैमाने का प्रतिफल

परिवर्तनीय अनुपातों का नियम इसलिये आविर्भूत होता है क्योंकि जब कारक अनुपातों में परिवर्तन होता है तक एक कारक स्थिर रखा जाता है तथा दूसरा बढ़ाया जाता है। यदि दोनों कारकों में परिवर्तन हो तो क्या होगा? ध्यान रखिये कि ऐसा दीर्घकाल में ही हो सकता है। दीर्घकाल में एक विशेष स्थिति होती है जब दोनों कारकों को समान अनुपात में बढ़ाया जाता है अथवा कारकों को ‘स्केल अप’ किया जाता है।

जब सभी आगतों मे समानुपातिक वृद्धि, निर्गत में उसी अनुपात में वृद्धि उत्पन्न करती है तो उत्पादन फलन पैमाने के स्थिर प्रतिफल को दर्शाता है (CRS) जब सभी आगतों में समानुपातिक वृद्धि, निर्गत में, अनुपात से अधिक वृद्धि उत्पन्न करती है, तो उत्पादन फलन पैमाने के वृद्धिमान उत्पादन फलन को दर्शाता है। (IRS) जब सभी आगतों के आनुपातिक वृद्धि की तुलना में, निर्गत में समानुपति वृद्धि कम होती है तो यह पैमाने के ह्रासमान प्रतिफल को दर्शाता है।

ह्रासमान पैमाने का प्रतिफल तब होता है, जब सभी आगतों के आनुपातिक वृद्धि की तुलना में निर्गत में समानुपाति वृद्धि कम होती है।

उदाहरण के लिए, मान लीजिए एक उत्पादन प्रक्रम में सभी आगत दोगुने हो जाते हैं। परिणामस्वरूप यदि निर्गत दोगुना हो जाता है, उत्पादन फलन स्थिर अनुमापी प्रतिफल को प्रदर्शित करता है। यदि निर्गत दोगुने की तुलना में कम है तो ह्रासमान अनुमापी प्रतिफल लागू होता है तथा यदि यह दोगुना से अधिक है तो वर्धमान अनुमापी प्रतिफल लागू होता है।

पैमाने का प्रतिफल

एक उत्पादन फलन पर विचार कीजिए

$$q=f(x_1,x_2)$$

जहाँ फर्म निर्गत की $q$ मात्रा का उत्पादन कारक 1 की $x_1$ मात्रा तथा कारक 2 के $x_2$ मात्रा का प्रयोग के द्वारा करती है। अब मान लीजिए कि फर्म दोनों कारकों के प्रयोग के स्तरों में $t(t>1)$ गुणा वृद्धि करने का निर्णय लेती है। गणितीय रूप में हम कह सकते हैं कि उत्पादन फलन प्रदर्शित करता है, स्थिर अनुमापी प्रतिफल को, यदि हमारे पास है।

$$f(t{x}_1,t{x}_2)=t.f(x_1,x_2)$$

उदाहरणार्थ, नया निर्गत स्तर $f(t{x}_1,t{x}_2)$ ठीक $t$ गुणा है, पूर्व निर्गत स्तर $f(x_1,x_2)$ की तुलना में।

समान रूप से, उत्पादन फलन प्रदर्शित करता है वर्धमान अनुमापी प्रतिफल को यदि

$$f(t{x}_1,t{x}_2)>t.f(x_1,x_2)$$

यह प्रदर्शित है ह्रासमान अनुमापी प्रतिफल को यदि

$$f(t{x}_1,t{x}_2)<t.f(x_1,x_2)$$

3.7 लागत

निर्गत का उत्पादन करने के लिए फर्म को आगतों का प्रयोग करने की आवश्यकता होती है। परंतु निर्गत के एक दिए गए स्तर का उत्पादन अनेक तरीकों से हो सकता है। एक से अधिक आगत संयोग हो सकते हैं, जिनसे एक फर्म निर्गत के इच्छित स्तर का उत्पादन कर सकती है। तालिका 3.1 में हम देख सकते हैं कि निर्गत की 50 इकाइयों का उत्पादन तीन भिन्न आगत संयोग $(\mathrm{L}=6,\mathrm{K}=3),(\mathrm{L}=4,\mathrm{K}=4)$ तथा $(\mathrm{L}=3,\mathrm{K}=6)$ द्वारा हो सकता है। प्रश्न है कि किस आगत संयोग का चयन फर्म करेगी? दिए गए आगत मूल्यों के साथ, वह चयन करेगी आगतों का वह संयोग, जो सबसे कम महंगा हो। अतः निर्गत के प्रत्येक स्तर के लिए एक न्यूनतम लागत फर्म के लिए होती है। इस प्रकार एक निश्चित उत्पादन कारक लागत एवं टेक्नोलोजी की दशा में लागत फलन, प्रत्येक स्तर पर उत्पादन की न्यूनतम लागत को बतलाता है।

कॉब-डगलस उत्पादन फलन

एक उत्पादन फलन पर विचार कीजिए

$$q=x_1{}^a{x}_2{}^b$$

जहाँ $\alpha$ तथा $\beta$ स्थिर है। फर्म निर्गत की $q$ मात्रा का उत्पादन कारक 1 की $x_1$ मात्रा तथा कारक 2 की $x_2$ मात्रा को प्रयोग में लाकर करती है। यह एक कॉब-डगलस उत्पादन फलन कहलाता है। मान लीजिए $x_1={\overline{x}}_1$ तथा $x_2={\overline{x}}_2$ के साथ हमारे पास निर्गत की $q_0$ इकाइयाँ हैं, अर्थात्

$$q_0={\overline{x}}_1{}^a{\overline{x}}_2{}^b.$$

यदि हम वृद्धि करते हैं $t(t>1)$ गुणा दोनों आगतों में, तो हमें नवीन निर्गत प्राप्त होता है:

$$\begin{array}{rl}{q}_1& ={\left(t{\overline{x}}_1\right)}^a{\left(t{\overline{x}}_2\right)}^b\\ & =t^{a+b}{\overline{x}}_1{}^a{\overline{x}}_2{}^b\end{array}$$

जब $\alpha +\beta =1$, हमारे पास है $q_1=t{q}_0$ इसका अभिप्राय है कि निर्गत में $t$ गुणा वृद्धि होती है। अतः उत्पादन फलन स्थिर पैमाना का प्रतिफल स्थिर अनुमापी प्रतिफल को प्रदर्शित करता है। इसी प्रकार से जब $\alpha +\beta >1$, उत्पादन फलन बढ़ते पैमाना का प्रतिफल को प्रदर्शित करता है। जब $\alpha +\beta <1$, उत्पादन फलन घटते पैमाना का प्रतिफल को प्रदर्शित करता है।

3.7.1 अल्पकालीन लागत

हमने पहले अल्पकाल तथा दीर्घकाल के विषय में चर्चा की है। अल्पकाल में उत्पादन के कुछ कारकों में परिवर्तन नहीं लाया जा सकता, अतः वे स्थिर रहते हैं। एक फर्म जो स्थिर लागतों का वहन करती है, उन्हें कुल स्थिर लागत कहते हैं। जितनी भी मात्रा का उत्पादन फर्म करती है, उसकी लागत फर्म के लिए स्थिर रहती है। किसी भी आवश्यक स्तर के निर्गत का उत्पादन करने

के लिए, अल्पकाल में फर्म केवल परिवर्ती आगतों को ही समायोजित कर सकती है। इसके अनुसार लागत जो एक फर्म इन परिवर्ती आगतों को प्रयोग करने के लिए वहन करती है, कुल परिवर्ती लागत कहलाती है। स्थिर तथा परिवर्ती लागतों को सम्मिलित करते हुए हमें एक फर्म की कुल लागत प्राप्त होती है।

$$\begin{array}{}\text{(3.5)}& \text{ कुल लागत = कुल परिवर्ती लागत + कुल स्थिर लागत }\end{array}$$

निर्गत के उत्पादन में वृद्धि करने के लिए फर्म को परिवर्ती आगतों में से अधिक प्रयोग करने की आवश्यकता होती है। परिणामस्वरूप, कुल परिवर्ती लागत तथा कुल लागत में भी वृद्धि होती है। अतः जब निर्गत में वृद्धि होती है, तो कुल परिवर्ती लागत एवं कुल लागत में वृद्धि होती है।

तालिका 3.3 में हमारे पास एक विशिष्ट फर्म के लागत फलन का उदाहरण है। प्रथम कॉलम निर्गत के विभिन्न स्तरों को दर्शाता है। निर्गत के सभी स्तरों के लिए कुल स्थिर लागत 20 रुपए हैं। जैसे-जैसे निर्गत में वृद्धि होती है, कुल परिवर्ती लागत में वृद्धि होती है। शून्य निर्गत के साथ कुल परिवर्ती लागत शून्य है। निर्गत की 1 इकाई के लिए कुल परिवर्ति लागत 10 रुपए है, निर्गत की दो इकाइयों के लिए कुल परिवर्ती लागत 18 रुपए है इत्यादि। जैसे कॉलम दो में कुल स्थिर लागत तथा कॉलम तीन में कुल परिवर्ती लागत के मूल्य को प्राप्त किया था, उसी प्रकार इसके जोड़ के रूप में हम कुल लागत को कॉलम चार में प्राप्त करते हैं। निर्गत के शून्य स्तर पर कुल लागत केवल स्थिर लागत होती है तथा इस प्रकार 20 रुपए के बराबर है। निर्गत की 1 इकाई के लिए कुल लागत 30 रुपए है, निर्गत की 2 इकाइयों के लिए कुल लागत 38 रुपए है इत्यादि।

अल्पकालीन औसत लागत फर्म द्वारा वहन की जाती है, जिसे निर्गत की प्रति इकाई मूल्य की कुल लागत के रूप में परिभाषित किया जाता है। इसकी गणना हम इस प्रकार करते हैं।

$$\begin{array}{}\text{(3.6)}& \text{ अल्पकालीन औसत लागत }=\frac{\text{ कुल लागत }}{q}\end{array}$$

तालिका 3.3 में हमें अल्पकालीन औसत लागत चतुर्थ कॉलम के मूल्य को प्रथम कॉलम के मूल्य से विभाजित करने के पश्चात् प्राप्त होती हैं। शून्य निर्गत पर अल्पकालीन औसत लागत अपरिभाषित है। प्रथम इकाई के लिए अल्पकालीन औसत लागत 30 रुपए है, निर्गत की 2 इकाइयों के लिए अल्पकालीन औसत लागत 19 रुपए है इत्यादि।

तालिका 3.3: लागत को विभिन्न संकल्पनाएँ

इसी प्रकार से, औसत परिवर्ती लागत परिभाषित होती है कुल परिवर्ती लागत, प्रति इकाई निर्गत के रूप में। हम इसकी गणना इस प्रकार करते हैं:

$$\begin{array}{}\text{(3.7)}& \text{औसत कुल परिवर्ती लागत}=\frac{\text{ कुल परिवर्ती लागत }}{q}\end{array}$$

इसके अलावा, औसत स्थिर लागत है।

$$\begin{array}{}\text{(3.8)}& \text{ औसत स्थिर लागत }=\frac{कुलस्थिरलागत}{q}\end{array}$$

स्पष्ट रूप से,

अल्पकालीन औसत लागत $=$ औसत परिवर्ती लागत + औसत स्थिर लागत

तालिका 3.3 में हम अल्पकालीन स्थिर लागत प्रथम कॉलम के अनुरूप मूल्य द्वारा द्वितीय कॉलम के मूल्य में भाग देकर समान रूप से प्राप्त करते हैं। इसी प्रकार से, हम तृतीय कॉलम के मूल्य को प्रथम कॉलम के मूल्य से विभाजित करके औसत परिवर्ती लागत कॉलम को प्राप्त करते हैं। निर्गत के 0 स्तर पर औसत स्थिर लागत और औसत परिवर्ती लागत अपरिभाषित होते हैं। निर्गत की प्रथम इकाई के लिए औसत स्थिर लागत 20 रुपए है तथा औसत परिवर्ती लागत 10 रुपए है। उन्हें जोड़कर हम अल्पकालीन औसत लागत 30 रुपए के बराबर प्राप्त करते हैं।

अल्पकालीन सीमांत लागत परिभाषित की जाती है कुल लागत में परिवर्तन प्रति इकाई निर्गत में परिवर्तन के रूप में।

$$\begin{array}{}\text{(3.10)}& \text{ अल्पकालीन सीमांत लागत }=\frac{\text{ कुल लागत में परिवर्तन }}{\text{ निर्गत में परिवर्तन }}=\frac{\mathrm{\Delta }\text{ कुल लागत }}{\mathrm{\Delta }q}\end{array}$$

जहाँ $\mathrm{\Delta }$ चर के मूल्य में परिवर्तन का प्रतिनिधित्व करता है।

तालिका 3.3 का अंतिम कॉलम, अल्पकालीन सीमांत लागत की गणना का एक संख्यात्मक उदाहरण प्रस्तुत करता है। इस कॉलम के मूल्यों की गणना प्रत्येक निर्गत पर कुल लागत मे परिवर्तन को, निर्गत में परिवर्तन से भाग देकर, प्राप्त की जाती हैं।

अत: $\mathrm{q}=5$ पर,

कुल सीमांत लागत में परिवर्तन $=(\mathrm{TC},\mathrm{q}=5$ पर $)-(\mathrm{TC},\mathrm{q}=4$ पर $)$

$$\begin{array}{}\text{(3.11)}& =(53)-(49)=4\end{array}$$

$\mathrm{q}\text{ में परिवर्तन }=1$

कुल सीमांत लागत $=4/1=4$

ठीक उसी प्रकार, सीमांत उत्पाद की तरह ही, सीमांत लागत भी निर्गत के शून्य स्तर पर अपरिभाषित है। यहाँ यह ध्यान देना महत्त्वपूर्ण है कि अल्पकाल में स्थिर लागत में परिवर्तन नहीं लाया जा सकता। जब हम निर्गत के स्तर में परिवर्तन करते हैं, तो जो भी परिवर्तन कुल लागत में होता है, वह पूरी तरह से कुल परिवर्ती लागत में परिवर्तन के कारण होता है। अतः निर्गत की एक अतिरिक्त इकाई के उत्पादन में वृद्धि के कारण जो कुल परिवर्ती लागत में वृद्धि होती है, वही अल्पकाल में सीमांत लागत है। निर्गत के किसी भी स्तर के लिए सीमांत लागतों का उस स्तर तक कुल जोड़, हमें उस स्तर पर कुल परिवर्ती लागत देता है। कोई भी इसे तालिका 3.3 में दर्शाए गए उदाहरण से समझ सकता है। निर्गत के किसी स्तर पर, औसत परिवर्ती लागतें, सभी सीमांत लागतों का औसत से ऊपर होती है। तालिका 3.3 में हम देखते हैं कि जब निर्गत शून्य है, तो अल्पकालीन सीमांत लागत अपरिभाषित है। निर्गत की प्रथम इकाई के लिए अल्पकालीन सीमांत लागत 10 रुपए है, द्वितीय इकाई के लिए अल्पकालीन सीमांत लागत 8 रुपए है तथा यह क्रम इसी प्रकार चलता रहता है।

अल्पकालीन लागत वक्र की आकृति

अब हम देखते हैं कि यह अल्पकालीन लागत वक्र कैसे दिखाई देते हैं? तालिका 3.3 में दिये गये समंको को, $\mathrm{X}$ अक्ष पर उत्पाद और $\mathrm{Y}$ अक्ष पर लागतों को दिखा सकते हैं।

पहले इसकी विवेचना की गई थी कि निर्गत के उत्पादन में वृद्धि करने के लिए फर्म को अधिक परिवर्ती आगतों के प्रयोग करने की आवश्यकता होती है। इसका परिणाम होता है कुल परिवर्ती लागत में वृद्धि तथा इसी प्रकार, कुल लागत में वृद्धि होती है। अतः जैसे-जैसे निर्गत में वृद्धि होती है, कुल परिवर्ती लागत तथा कुल लागत में वृद्धि होती जाती है। कुल स्थिर लागत यद्यपि स्वतंत्र है, उत्पादित निर्गत की मात्रा से तथा उत्पादन के सभी स्तरों पर यह स्थिर रहती है।

रेखाचित्र 3.3

लागतः यह कुल स्थिर लागत है। एक फर्म के लिए कुल परिवर्तो लागत तथा कुल लागत वक्र कुल लागत, कुल स्थिर लागत तथा कुल परिवर्ती लागत का उदग्र जोड़ है।

रेखाचित्र 3.3 दर्शाती है कुल स्थिर लागत, कुल परिवर्ती लागत तथा कुल लागत वक्र का आकार, एक विशिष्ट फर्म के लिए है। हम उत्पाद को $x$ अक्ष पर तथा लागतों को $y$ अक्ष पर दिखाते हैं। कुल स्थिर लागत स्थिर है, जो मूल्य $c_1$ लेता है तथा निर्गत में परिवर्तन के साथ परिवर्तित नहीं होता। अतः यह एक समस्तरीय सीधी रेखा है जो लागत अक्ष के बिंदु $c_1$ पर काटती है। $q_1$ पर कुल परिवर्ती लागत है $c_2$ तथा कुल लागत है $c_3$ ।

औसत स्थिर लागत कुल स्थिर लागत का अनुपात $q$ है। कुल स्थिर लागत स्थिर है। अतः जैसे-जैसे $q$ में वृद्धि होती है, औसत स्थिर लागत घटती जाती है। जब निर्गत शून्य के अत्यधिक निकट होता है, औसत स्थिर लागत मनमाने ढंग से बड़ा होता है तथा निर्गत जैसे-जैसे अनंत की ओर बढ़ता है, औसत स्थिर लागत शून्य की ओर बढ़ती है। औसत स्थिर लागत वक्र वास्तव में एक आयताकार अतिपरवलय है। यदि हम निर्गत के किसी भी मूल्य $q$ को उससे संबंधित औसत स्थिर लागत से गुणा करते हैं, तब हम सदैव एक स्थिर कुल स्थिर लागत प्राप्त करते हैं।

रेखाचित्र 3.4 एक विशिष्ट फर्म के लिए औसत स्थिर लागत वक्र का आकार दर्शाता है।

रेखाचित्र 3.4

औसत स्थिर लागतः औसत स्थिर लागत वक्र है एक आयताकार अतिपरवलय। आयत $OFC{q}_1$ हमें कुल स्थिर लागत का क्षेत्रफल देता है।

हम समस्तरीय अक्ष पर निर्गत मापते हैं तथा औसत स्थिर लागत ऊर्ध्वस्तर अक्ष पर। निर्गत के $q_1$ स्तर पर हम औसत स्थिर लागत $F$ पर प्राप्त करते हैं। कुल स्थिर लागत की गणना इस प्रकार की जा सकती है।

कुल स्थिर लागत $=$ औसत स्थिर लागत $\times$ मात्रा

$$\begin{array}{rl}& =OF\times O{q}_1\\ & =\text{ आयत }OFC{q}_1\text{ का क्षेत्रफल }\end{array}$$

हम कुल स्थिर लागत वक्र से भी औसत स्थिर लागत की गणना कर सकते हैं। रेखाचित्र 3.5 में समस्तरीय सीधी रेखा ऊध्र्वस्तर अक्ष को $F$ पर काटती है, वह कुल स्थिर लागत वक्र है। निर्गत के $q_0$ स्तर पर कुल स्थिर लागत $OF$ के समान है। $q_0$ पर कुल स्थिर लागत वक्र पर संबंधित बिंदु $A$ है। अब $\mathrm{\angle }AO{q}_0$ होगा $\theta$.

$q_0$ पर औसत स्थिर लागत है:

औसत स्थिर लागत $=$

$$\frac{\text{ कुल स्थिर लागत }}{\text{ मात्रा }}=\frac{A{q}_0}{O{q}_0}=\tan \theta$$

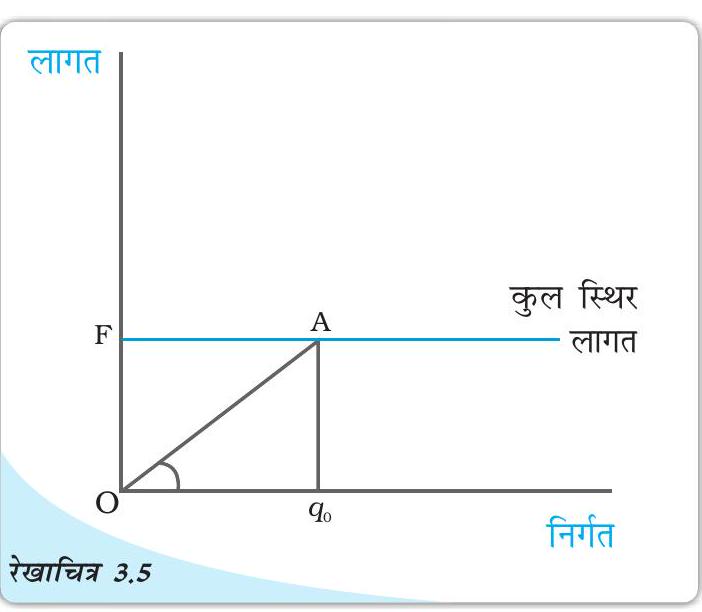
कुल स्थिर लागत वक्र $\mathrm{\angle }Aoqo$ का ढाल हमें $q_o$ पर औसत स्थिर लागत देता है।

आइए, अब दृष्टि डालते हैं अल्पकालीन सीमांत लागत वक्र पर। सीमांत लागत वह अतिरिक्त लागत है जो एक फर्म निर्गत की एक अतिरिक्त इकाई का उत्पादन करने के लिए अपने ऊपर वहन करती है। परिवर्ती अनुपात के नियम के अनुसार, आरंभ में एक कारक के सीमांत उत्पाद में वृद्धि होती है। जैसे-जैसे प्रयोग में वृद्धि होती जाती है, एक विशेष बिंदु पर पहुँचकर इसमें गिरावट आने लगती है। इससे अभिप्राय है कि आरंभ में निर्गत की प्रत्येक अगली इकाई का उत्पादन करने के लिए कारक की आवश्यकता न्यूनतम होती जाती है और तदुपरांत एक विशेष बिंदु पर पहुँचने के पश्चात् यह अधिकतम होती जाती है। परिणामस्वरूप, दिए गए कारक मूल्य के साथ आरंभ में अल्पकालीन सीमांत लागत में गिरावट आती है तथा उसके बाद एक विशेष बिंदु पर पहुँचकर इसमें वृद्धि होने लगती है। अतः अल्पकालीन सीमांत लागत वक्र $U$ आकार की होती है।

निर्गत के शून्य स्तर पर अल्पकालीन सीमांत लागत अपरिभाषित होती है। निर्गत के एक विशेष स्तर पर, कुल परवर्ती लागत, उस स्तर पर सभी सीमांत लागातों का योग होती है।

अब औसत परिवर्ती लागत वक्र किस प्रकार दिखता है? निर्गत की प्रथम इकाई के लिए यह जाँच करना सरल है कि अल्पकालीन सीमांत लागत तथा औसत परिवर्ती लागत एक ही हैं। अतः दोनों अल्पकालीन सीमांत लागत तथा औसत परिवर्ती लागत वक्र एक ही बिंदु से शुरू होते हैं। फिर जैसे-जैसे निर्गत में वृद्धि होती जाती है, अल्पकालीन सीमांत लागत में गिरावट आती है।

औसत परिवर्ती लागत सीमांत लागतों का औसत लागत होने के कारण उसमें गिरावट आने लगती है। परंतु, अल्पकालीन सीमांत लागत की तुलना में कम गिरावट आती है। तब एक बिंदु के बाद, अल्पकालीन सीमांत लागत में वृद्धि होने लगती है। औसत परिवर्ती लागत में निंरतर गिरावट आती है। जब तक अल्पकालीन सीमांत लागत का मूल्य प्रचलित औसत परिवर्ती लागत के मूल्य की तुलना में कम रहता है। एक बार, जब अल्पकालीन सीमांत लागत में पर्याप्त रूप से वृद्धि हो जाती है, इसका मूल्य औसत परितवर्ती लागत के मूल्य की तुलना में अधिक हो जाता है। तब औसत परिवर्ती लागत में वृद्धि आनी आरंभ हो जाती है। अतः औसत परिवर्ती लागत वक्र ‘U’ आकार का होती है।

जब तक औसत परिवर्ती लागत में गिरावट आती रहती है, अल्पकालीन सीमांत लागत को औसत परिवर्ती लागत की तुलना में आवश्यक रूप से कम होना ही चाहिए तथा जैसे-जैसे औसत परिवर्ती लागत में वृद्धि होती है, अल्पकालीन सीमांत लागत को औसत परिवर्ती लागत की तुलना में आवश्यक रूप से अधिक होना ही चाहिए। अतः अल्पकालीन सीमांत लागत वक्र, औसत परिवर्ती लागत वक्र को नीचे से औसत परिवर्ती लागत के न्यूनतम बिंदु पर काटता है।

औसत परिवर्ती लागत वक्र आयत $OVB{q}_0$ का क्षेत्रफल देता है कुल परिवर्तो लागत $q_0$ पर।

रेखाचित्र 3.6 में हम निर्गत को समस्तरीय अक्ष पर तथा औसत परिवर्ती लागत को ऊर्ध्रस्तर अक्ष पर मापते हैं। निर्गत के $q_0$ स्तर पर औसत परिवर्ती लागत, $\mathrm{OV}$ के समान है। $q_0$ पर कुल परिवर्ती लागत है:

कुल परिवर्ती लागत $=$ औसत परिवर्ती लागत $\times$ मात्रा

$$\begin{array}{rl}& =OV\times O{q}_0\\ & =\text{ आयत }\mathrm{OVB}{q}_0\text{ का क्षेत्रफल }\end{array}$$

रेखाचित्र 3.7 में हम समस्तरीय अक्ष पर निर्गत मापते हैं तथा ऊर्ध्वस्तर अक्ष पर कुल परिवर्ती लागत। निर्गत के $q_0$ स्तर पर $\mathrm{OV}$ कुल परिवर्ती लागत है। मान लीजिए कोण $\mathrm{\angle }{\mathrm{EOq}}_0,\theta$ के बराबर है। तब $q_0$ पर औसत परिवर्ती लागत की गणना निम्न रूप में की जा सकती है:

औसत परिवर्ती लागत $=\frac{\text{ कुल परिवर्ती लागत }}{\text{ निर्गत }}$

$$=\frac{E{q}_0}{O{q}_0}=\tan$$

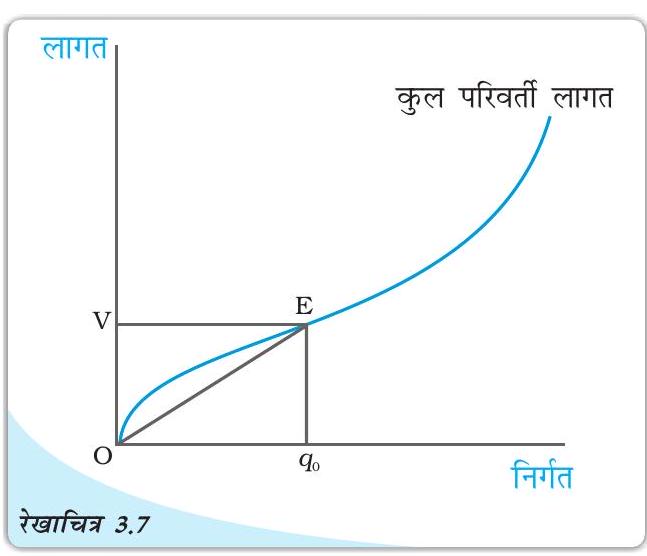
कुल परिवर्ती लागत वक्र: कोण $\mathrm{\angle }EO{q}_0$ की प्रवणता हमें $q_o$ पर औसत परिवर्ती लागत प्रदान करता है।

आइए, अब अल्पकालीन औसत लागत पर दृष्टि डालते हैं। अल्पकालीन औसत लागत औसत परिवर्ती लागत तथा औसत स्थिर लागत का जोड़ है। आरंभ में दोनों औसत परिवर्ती लागत तथा औसत स्थिर लागत में गिरावट आती है, जैसे-जैसे निर्गत में वृद्धि होती है। अतः अल्पकालीन औसत लागत में आरंभ में गिरावट आती है। $\mathrm{AVC}$ बढ़ने लगती है लेकिन $\mathrm{AFC}$ लगातार गिरती रहती है। प्रारंभ में $\mathrm{AFC}$ में गिरावट, $\mathrm{AVC}$ की वृद्धि की अपेक्षा अधिक होती है और $\mathrm{SAC}$ अभी भी गिर रही है। परन्तु उत्पादन के एक स्तर के पश्चात, $\mathrm{AVC}$ में वृद्धि, $\mathrm{AFC}$ की गिरावट की अपेक्षा अधिक है। इस बिन्दु के बाद से आगे, $\mathrm{SAC}$ बढ़ रही है। SAC वक्र इसलिए ’ $U$ ’ आकार का होता है।

यह औसत परिवर्ती अल्पकालीन लागत वक्र के ऊपर ऊर्ध्वस्तर भिन्नता के साथ स्थित होता है, जो औसत स्थिर लागत के मूल्य के समान है। अल्पकालीन औसत लागत वक्र का न्यूनतम बिंदु दाहिनी ओर स्थित है, औसत परिवर्ती लागत वक्र के न्यूनतम बिंदु से।

औसत परिवर्ती लागत तथा अल्पकालीन सीमांत लागत के स्थिति के समान ही, यहाँ पर भी जब तक अल्पकालीन औसत लागत में गिरावट आती है, अल्पकालीन औसत लागत की तुलना में अल्पकालीन सीमांत लागत कम होती है तथा जब अल्पकालीन औसत लागत में वृद्धि होती है, अल्पकालीन औसत लागत की तुलना में अल्पकालीन सीमांत लागत अधिक होती है। अल्पकालीन सीमांत लागत वक्र अल्पकालीन औसत लागत वक्र को अल्पकालीन औसत लागत के न्यूनतम बिंदु पर नीचे से काटता है,

अल्पकालीन लागतः अल्पकालीन सीमांत लागत, औसत परिवर्ती लागत तथा औसत लागत वक्र।

रेखाचित्र 3.8 एक विशिष्ट फर्म के लिए अल्पकालीन सीमांत लागत, औसत परिवर्ती लागत तथा अल्पकालीन औसत लागत वक्र की आकृति को दर्शाता है। औसत परिवर्ती लागत निर्गत की $q_1$ इकाइयों पर इसके न्यूनतम बिंदु पर पहुँचती है। $q_1$ के बायों ओर औसत परिवर्ती लागत में गिरावट आ रही है तथा अल्पकालीन सीमांत लागत, औसत परिवर्ती लागत की तुलना में कम है। $q_1$ के दाहिनी ओर औसत परिवर्ती लागत में वृद्धि हो रही है तथा अल्पकालीन सीमांत लागत औसत परिवर्ती लागत की तुलना में अधिक है। अल्पकालीन सीमांत लागत वक्र ’ $P$ ’ पर औसत परिवर्ती लागत वक्र को काटता है, जो औसत परिवर्ती लागत वक्र का न्यूनतम बिंदु है। न्यूनतम बिंदु अल्पकालीन औसत लागत वक्र का ’ $S$ ’ है, जो निर्गत $q_2$ को प्रदर्शित करता है। यह अल्पकालीन सीमांत लागत तथा अल्पकालीन औसत लागत वक्र के मध्य परिच्छेदन बिंदु है। $q_2$ के बायों ओर अल्पकालीन औसत लागत में गिरावट आ रही है तथा अल्पकालीन सीमांत लागत, अल्पकालीन औसत लागत की तुलना में कम है। $q_2$ से दाहिनी ओर अल्पकालीन औसत लागत में वृद्धि हो रही है तथा अल्पकालीन सीमांत लागत, अल्पकालीन औसत लागत की तुलना में अधिक है।

3.7.2 दीर्घकालीन लागत

दीर्घकाल में, सभी आगत परिवर्त होते हैं। कोई स्थिर लागतें नहीं होती। अतः कुल लागत तथा कुल परिवर्ती लागत दीर्घकाल में एक ही समय में घटित होते हैं। दीर्घकालीन औसत लागत पारिभाषित की जाती है, प्रति इकाई निर्गत लागत के रूप में अर्थात्

$$\begin{array}{}\text{(3.12)}& \text{ दीर्घकालीन औसत लागत }=\frac{\text{ कुल लागत }}{q}\end{array}$$

दीर्घकालीन सीमांत लागत कुल लागत में वह परिवर्तन है, जो प्राप्त इकाई निर्गत में परिवर्तन के फलस्वरूप होती है। जब विच्छिन्न इकाई में निर्गत बदलता है, तब यदि हम उत्पादन में वृद्धि करें $q_1-1$ से $q_1$ निर्गत इकाइयों तक, तो $q_1$ वीं इकाई का उत्पादन करने की सीमांत लागत इस प्रकार मापी जाएगी:

दीर्घकालीन सीमांत लागत $=(q_1$ इकाइयों पर कुल लागत $)-(q_1$ इकाइयों पर कुल लागत $)$

अल्पकाल के समान ही दीर्घकाल में सभी सीमांत लागत का कुल जोड़ कुछ निर्गत स्तर तक कुल लागत देता है।

दीर्घकालीन लागत वक्रों का आकार

हमने पहले पैमाने का प्रतिफल के विषय में विवेचन किया है। आइए, अब दीर्घकालीन औसत लागत वक्र पर उसके अकार को देखते हैं। वर्धमान पैमाना का प्रतिफल से अभिप्राय है कि यदि हम सभी आगतों में वृद्धि एक विशेष अनुपात से कर दें, तो निर्गत में उस अनुपात की तुलना में अधिक वृद्धि होती है। दूसरे शब्दों में, निर्गत में एक विशेष अनुपात की वृद्धि करने के लिए आगतों में उस अनुपात की तुलना में कम वृद्धि करने की आवश्यकता है। जब निर्गत की कीमत दिये हुए हों, लागत में भी कम अनुपात में वृद्धि होती है। उदाहरण के लिए, मान लीजिए हम निर्गत को दोगुना करने के इच्छुक हैं। ऐसा करने के लिए आगतों में दोगुना से कम वृद्धि की आवश्यकता है। लागत, जो फर्म अपने ऊपर लेती है, उन आगतों को किराए पर लेने के लिए भी, दोगुना से कम वृद्धि की आवश्यकता है। यहाँ औसत लागत पर क्या प्रभाव पड़ रहा है? निःसंदेह यह स्थिति तब होगी, जब तक वर्धमान पैमाना का प्रतिफल कार्य करेगा। जैसे-जैसे फर्म निर्गत में वृद्धि करती रहेगी, औसत लागत गिरता रहेगा।

ह्रासमान पैमाने का प्रतिफल से अभिप्राय है कि यदि हम निर्गत में वृद्धि एक विशेष अनुपात से करने के इच्छुक हैं, तो आगतों में उस अनुपात की तुलना में अधिक वृद्धि करने की आवश्यकता है। परिणामस्वरूप, लागत में भी वृद्धि उस अनुपात की तुलना में अधिक होती है। अतः जब तक ह्रासमान पैमाना का प्रतिफल कार्य करता है, औसत लागत में वृद्धि होनी चाहिए, जब भी फर्म निर्गत में वृद्धि करती है।

स्थिर पैमाने का प्रतिफल से अभिप्राय है, आगतों में एक आनुपातिक वृद्धि के परिणामस्वरूप निर्गत में एक आनुपातिक वृद्धि। अतः औसत लागत जब तक स्थिर रहता है, तब तक स्थिर पैमाना का प्रतिफल कार्य करता है।

ऐसा तर्क दिया जाता है कि एक विशिष्ट फर्म वर्धमान पैमाना का प्रतिफल में उत्पादन के आरंभिक स्तर पर दिखलाई पड़ता है। इसका अनुसरण स्थिर पैमाना का प्रतिफल द्वारा तथा फिर ह्रासमान पैमाना का प्रतिफल द्वारा होता है। इसके अनुसार दीर्घकालीन औसत लागत वक्र एक ‘U’

आकार का वक्र है। इसके नीचे की ओर प्रवण भाग संबद्ध रहता है। वर्धमान पैमाने का प्रतिफल से तथा ऊपर की ओर उठता हुआ भाग संबद्ध रहता है, ह्रासमान पैमाने का प्रतिफल से। दीर्घकालीन औसत लागत वक्र के न्यूनतम बिन्दु पर स्थिर पैमाने का प्रतिफल दिखलाई पड़ता है। आइए, अब जाँच करते हैं किस प्रकार दीर्घकालीन सीमांत लागत वक्र दिखता है। निर्गत की प्रथम इकाई के लिए दीर्घकालीन सीमांत लागत तथा दीर्घकालीन औसत लागत समान होता है। अब जब निर्गत में वृद्धि हो जाती है, तो दीर्घकालीन औसत लागत में आरंभ में गिरावट आती है और तदुपरांत एक विशेष बिंदु के पश्चात इसमें वृद्धि होने लगती है। जब तक औसत लागत में गिरावट आती है, सीमांत लागत आवश्यक रूप से औसत लागत की तुलना में कम होनी चाहिए। जब औसत लागत में वृद्धि हो रही हो, सीमांत लागत औसत लागत की तुलना में अधिक होगी। अत: दीर्घकालीन औसत लागत वक्र एक ’ $U$ ’ आकार का वक्र है। यह दीर्घकालीन औसत लागत वक्र को नीचे से दीर्घकालीन औसत लागत के न्यूनतम बिंदु पर काटता है। रेखाचित्र 3.9 एक विशिष्ट फर्म के

दीर्घकालीन लागतः दीर्घकालीन सीमांत लागत तथा औसत लागत वक्र। लिए दीर्घकालीन सीमांत लागत तथा दीर्घकालीन औसत वक्र का आकार दर्शांता है।

दीर्घकालीन औसत लागत $q_1$ पर अपने न्यूनतम पर पहुँचती है। $q_1$ के बायों ओर दीर्घकालीन औसत लागत में गिरावट आ रही है तथा दीर्घकालीन सीमांत लागत, दीर्घकालीन औसत लागत वक्र की तुलना में कम है। $q_1$ के दाहिनी ओर दीर्घकालीन औसत लागत में वृद्धि हो रही है तथा दीर्घकालीन सीमांत लागत, दीर्घकालीन औसत लागत की तुलना में ऊँची है।

3.8 सारांश

• आगतों के विभिन्न सम्मिश्रण के लिए उत्पादन फलन निर्गत की अधिकतम मात्रा दर्शाता है, जिस पर उत्पादन संभव है।
• अल्पकाल में कुछ आगतों में परिवर्तन नहीं किया जा सकता। दीर्घकाल में सभी आगतों में परिवर्तन किया जा सकता है।
• कुल उत्पाद, परिवर्ती आगत तथा निर्गत से संबंधित है, ऐसी स्थिति में जब अन्य सभी आगतों को स्थिर रखा जाए।
• एक आगत के प्रयोग के किसी भी स्तर के लिए, सीमांत उत्पादों का कुल जोड़, उस आगत की प्रति इकाई प्रयोग के स्तर पर, उस आगत के लिए कुल उत्पाद प्रदान करता है।
• सीमांत उत्पाद तथा औसत उत्पाद वक्र दोनों उल्टे ’ $\mathrm{U}$ ’ के आकार में है। सीमांत उत्पाद वक्र औसत उत्पाद वक्र को ऊपर से, औसत उत्पाद वक्र के अधिकतम बिंदु पर काटता है।
• निर्गत का उत्पादन करने के लिए फर्म सबसे कम लागत वाले आगत संयोग का चयन करती है।
• कुल लागत, कुल परिवर्ती लागत तथा कुल स्थिर लागत का जोड़ है।
• औसत लागत जोड़ है, औसत परिवर्ती लागत तथा औसत स्थिर लागत का।
• औसत स्थिर लागत वक्र नीचे की ओर प्रवणता वाली है।
• अल्पकालीन सीमांत लागत, औसत परिवर्ती लागत तथा अल्पकालीन औसत लागत वक्र ‘U’ आकार के होते हैं।
• अल्पकालीन सीमांत लागत वक्र, औसत परिवर्ती लागत वक्र को नीचे से औसत परिवर्ती लागत के न्यूनतम बिन्दु पर काटता है।
• अल्पकालीन सीमांत लागत वक्र, अल्पकालीन औसत लागत वक्र को नीचे से अल्पकालीन औसत लागत के न्यूनतम बिन्दु पर काटता है।
• निर्गत के किसी भी स्तर के लिए, अल्पकाल में सीमांत लागतों का कुल जोड़ हमें उस स्तर तक कुल परिवर्ती लागत प्रदान करता है। अल्पकालीन परिवर्ती लागत वक्र के अंदर का क्षेत्रफल निर्गत के किसी भी स्तर तक हमें उस स्तर तक के लिए कुल परिवर्ती लागत देता है।
• दीर्घकालीन औसत लागत तथा दीर्घकालीन सीमांत लागत दोनों वक्र ‘U’ आकार के होते हैं।
• दीर्घकालीन सीमांत लागत वक्र दीर्घकालीन औसत लागत वक्र को नीचे से दीर्घकालीन औसत लागत के न्यूनतम बिंदु पर काटता है।

3.9 मुख्य संकल्पनाएँ

3.10 अभ्यास

1. उत्पादन फलन की संकल्पना को समझाइए।

2. एक आगत का कुल उत्पाद क्या होता है?

3. एक आगत का औसत उत्पाद क्या होता है?

4. एक आगत का सीमांत उत्पाद क्या होता है?

5. एक आगत के सीमांत उत्पाद तथा कुल उत्पाद के बीच संबंध समझाइए।

6. अल्पकाल तथा दीर्घकाल के संकल्पनाओं को समझाइए।

7. ह्रासमान सीमांत उत्पाद का नियम क्या है?

8. परिवर्ती अनुपात का नियम क्या है?

9. एक उत्पादन फलन स्थिर पैमाना का प्रतिफल को कब संतुष्ट करता है?

10. एक उत्पादन फलन वर्धमान पैमाना का प्रतिफल को कब संतुष्ट करता है?

11. एक उत्पादन फलन ह्रासमान पैमाना का प्रतिफल को कब संतुष्ट करता है?

12. लागत फलन की संकल्पनाओं को संक्षिप्त में समझाइए।

13. एक फर्म का कुल स्थिर लागत, कुल परिवर्ती लागत तथा कुल लागत क्या है, वे किस प्रकार संबंधित है?

14. एक फर्म की औसत स्थिर लागत, औसत परिवर्ती लागत तथा औसत लागत क्या है, वे किस प्रकार संबंधित हैं?

15. क्या दीर्घकाल में कुछ स्थिर लागत हो सकती है? यदि नहीं तो क्यों?

16. औसत लागत वक्र कैसा दिखता है? यह ऐसा क्यों दिखता है?

17. अल्पकालीन सीमांत लागत, औसत परिवर्ती लागत तथा अल्पकालीन औसत लागत वक्र कैसे दिखाई देते हैं?

18. क्यों अल्पकालीन सीमांत लागत वक्र औसत परिवर्ती लागत वक्र को काटता है, औसत परिवर्ती लागत वक्र के न्यूनतम बिंदु पर?

19. किस बिंदु पर अल्पकालीन सीमांत लागत वक्र अल्पकालीन औसत लागत को काटता है। अपने उत्तर के समर्थन में कारण बताइए।

20. अल्पकालीन सीमांत लागत वक्र ’ $U$ ’ आकार का क्यों होता है?

21. दीर्घकालीन सीमांत लागत तथा औसत लागत वक्र कैसे दिखते हैं?

22. निम्नलिखित तालिका, श्रम का कुल उत्पादन अनुसूची देती है। तदनुरूप श्रम का औसत उत्पाद तथा सीमांत उत्पाद अनुसूची निकालिए।

23. नीचे दी हुई तालिका, श्रम का औसत उत्पाद अनुसूची बताती है। कुल उत्पाद तथा सीमांत उत्पाद अनुसूची निकालिए, जबकि श्रम प्रयोगता के शून्य स्तर पर यह दिया गया है कि कुल उत्पाद शून्य है,

24. निम्नलिखित तालिका श्रम का सीमांत उत्पाद अनुसूची देती है। यह $L$ सीमांत उत्पाद भी दिया गया है कि श्रम का कुल उत्पाद शून्य है। प्रयोग के शून्य स्तर पर श्रम के कुल उत्पाद तथा औसत उत्पाद अनुसूची की गणना कीजिए।

25. नीचे दी गई तालिका एक फर्म की कुल लागत अनुसूची दर्शाती है। इस फर्म का कुल स्थिर लागत क्या है। फर्म के कुल परिवर्ती लागत, कुल स्थिर लागत, औसत परिवर्ती लागत, अल्पकालीन औसत लागत तथा अल्पकालीन सीमांत लागत अनुसूची की गणना कीजिए।

26. निम्नलिखित तालिका एक फर्म के लिए कुल लागत अनुसूची देती है। यह भी दिया गया है कि औसत स्थिर लागत निर्गत की 4 इकाइयों पर 5 रुपए है। कुल परिवर्ती लागत, कुल स्थिर लागत, औसत परिवर्ती लागत, औसत स्थिर लागत, अल्पकालीन औसत लागत, अल्पकालीन सीमांत लागत अनुसूची फर्म के निर्गत के तद्नुरूप मूल्यों के लिए निकालिए,

27. एक फर्म का अल्पकालीन सीमांत लागत अनुसूची निम्नलिखित तालिका में दिया गया है। फर्म की कुल स्थिर लागत 100 रुपए है। फर्म के कुल परिवर्ती लागत, कुल लागत, औसत परिवर्ती लागत तथा अल्पकालीन औसत लागत अनुसूची निकालिए।

28. मान लीजिए, एक फर्म का उत्पादन फलन है,

$\mathrm{Q}=5L^{\frac{1}{2}}{K}^{\frac{1}{2}}$

निकालिए, अधिकतम संभावित निर्गत जिसका उत्पादन फर्म कर सकती है 100 इकाइयाँ $L$ तथा 100 इकाइयाँ $K$ द्वारा।

29. मान लीजिए, एक फर्म का उत्पादन फलन है,

$Q=2L^2{K}^2$

अधिकतम संभावित निर्गत ज्ञात कीजिए, जिसका फर्म उत्पादन कर सकती है, 5 इकाइयाँ

$L$ तथा 2 इकाइयाँ $K$ द्वारा। अधिकतम संभावित निर्गत क्या है, जिसका फर्म उत्पादन कर सकती है शून्य इकाई $L$ तथा 10 इकाई $K$ द्वारा?

30. एक फर्म के लिए शून्य इकाई $L$ तथा 10 इकाइयाँ $K$ द्वारा अधिकतम संभावित निर्गत निकालिए, जब इसका उत्पादन फलन है:

$Q=5L+2K$