इस अध्याय में हम एक व्यक्तिगत उपभोक्ता के व्यवहार का अध्ययन करेंगे। उपभोक्ता को यह निर्णय करना होता है कि वह अपनी आय को विभिन्न वस्तुओं पर किस प्रकार व्यय करें। अर्थशास्त्री इसे चुनाव की समस्या कहते हैं। अतः स्वाभाविक रूप से, कोई भी उपभोक्ता वस्तुओं के ऐसे संयोजन को प्राप्त करना चाहेगा जो उसे अधिकतम संतोष प्रदान करता है। यह ‘सर्वोत्तम संयोग’ क्या होगा? यह उपभोक्ता की रुचियों और वह कितना व्यय कर सकता है, वस्तुओं की कीमतों और उसकी आय पर निर्भर करता है। यह अध्याय, उपभोक्ता व्यवहार को समझाने वाले दो भिन्न सिद्धांतों को प्रस्तुत करता है।

प्रारंभिक संकेतन तथा अभिग्रह

उपभोक्ता सामान्य रूप से बहुत-सी वस्तुओं का उपभोग करता है, परंतु सरलीकरण के लिए हम उपभोक्ता की चयन समस्या पर ऐसी स्थिति में विचार करेंगे, जहाँ केवल दो ही वस्तुएँ हों। हम इन दोनों वस्तुओं को केला तथा आम कहेंगे। दोनों वस्तुओं की मात्राओं की कोई भी सम्मिलित राशि को उपभोक्ता बंडल अथवा संक्षेप में बंडल कह सकते हैं। सामान्यतः हम केले की मात्रा को व्यक्त करने के लिए $x_{1}$ परिवर्त का और आम की मात्रा को व्यक्त करने के लिए $x_{2}$ परिवर्त का उपयोग करेंगे। $x_{1}$ और $x_{2}$ धनात्मक या शून्य हो सकते हैं। $\left(x_{1}, x_{2}\right)$, का तात्पर्य होगा कि केला की $x_{1}$ मात्रा तथा आम की $x_{2}$ मात्रा। $x_{1}$ तथा $x_{2}$ के किसी विशेष मूल्य के लिए $\left(x_{1}, x_{2}\right)$, हमें एक विशेष बंडल प्रदान करती है। उदाहरणार्थ- बंडल $(5,10)$ में केले की 5 इकाइयाँ और आम की 10 इकाइयाँ हैं; बंडल $(10,5)$ में केले की 10 इकाइयाँ और आम की 5 इकाइयाँ हैं।

2.1 उपयोगिता

सामान्यतः एक उपभोक्ता किसी वस्तु के लिए अपनी माँग का अनुमान उस उपयोगिता (अथवा संतोष) के आधार पर लगाता है जो वह उससे प्राप्त करता है। उपयोगिता क्या है? एक वस्तु की उपयोगिता, उसकी किसी आवश्यकता को संतुष्ट करने की क्षमता है। वस्तु की जितनी ज्यादा आवश्यकता होती है अथवा उसको प्राप्त करने की जितनी ज़्यादा इच्छा होती है, उस वस्तु से उतनी ही अधिक उपयोगिता प्राप्त होती है।

उदाहरण के लिए, एक व्यक्ति जो चॉकलेट पसंद करता है उसे एक चॉकलेट से अधिक उपयोगिता प्राप्त होगी उस व्यक्ति को किसी वस्तु से मिलने वाली उपयोगिता, स्थान एवं समय के साथ भी बदल सकती है। जैसे एक ‘रूम हीटर’ से मिलने वाली उपयोगिता इस बात पर निर्भर करेगी कि वह व्यक्ति लद्दाख में है अथवा चेन्नई में (स्थान) अथवा वहाँ गर्मी का मौसम है या ठण्ड का मौसम।

2.1.1 गणनावाचक उपयोगिता विश्लेषण

गणनावाचक उपयोगिता विश्लेषण की मान्यता है कि उपयोगिता के स्तर को संख्याओं में व्यक्त किया जा सकता है। उदाहरण के लिए, एक कमीज़ से प्राप्त उपयोगिता को माप सकते है, और कहें कि यह कमीज़ मुझे 50 इकाई उपयोगिता प्रदान करती है। आगे चर्चा करने से पूर्व, यह उपयोगी होगा कि हम उपयोगिता के दो महत्वपूर्ण मापों को समझें।

उपयोगिता के उपाय

कुल उपयोगिता: कुल उपयोगिता (TU) एक वस्तु की एक निश्चित मात्रा से प्राप्त उपयोगिता का योग है जो किसी वस्तु $(\mathrm{X})$ की दी गई मात्रा को उपयोग करने से प्राप्त होती है। वस्तु $\mathrm{X}$ की अधिक मात्रा, उपभोक्ता को अधिक संतोष प्रदान करती है। अतः $\mathrm{TU}$ वस्तु की उपयोग की गई मात्रा पर निर्भर करती है। अतः $\mathrm{TU}_{\mathrm{n}}$ वस्तु $\mathrm{X}$ की $\mathrm{n}$ इकाइयों के उपभोग से प्राप्त कुल उपयोगिता होती है।

सीमांत उपयोगिता

सीमांत उपयोगिता (MU) कुल उपयोगिता में वह परिवर्तन है जो वस्तु की एक अतिरिक्त इकाई के उपभोग से होता है। उदाहरण के लिए, मान लीजिये 4 केलों से हमें 28 इकाई कुल उपयोगिता प्राप्त होती है और 5 केलों से कुल उपयोगिता 30 इकाई मिलती है। स्पष्ट है कि पाँचवे केले के उपभोग से कुल उपयोगिता 2 इकाई बढ़ गई ( 30 इकाइयाँ– 28 इकाइयाँ), इसलिए पाँचवे केले की सीमांत उपयोगिता 2 इकाई है।

$\mathrm{MU} _{5}=\mathrm{TU} _{5}-\mathrm{TU} _{4}=30-28=2$

साधारण रूप में, $\mathrm{MU} _{\mathrm{n}}=\mathrm{TU} _{\mathrm{n}}-\mathrm{TU} _{\mathrm{n}-1}$, जहाँ पर $\mathrm{n}$ का अर्थ है, वस्तु की $\mathrm{n}^{\text {th }}$ इकाई।

कुल उपयोगिता और सीमांत उपयोगिता को निम्न तरीके से भी सम्बन्धित किया जा सकता है:$\mathrm{TU} _{\mathrm{n}}=\mathrm{MU} _{1}+\mathrm{MU} _{2}+\ldots \ldots . .+\mathrm{MU} _{\mathrm{n}-1}+\mathrm{MU} _{\mathrm{n}}$ सरल रूप में इसका अर्थ है कि केलों की $\mathrm{n}$ इकाइयों के उपभोग से प्राप्त उपयोगिता, सीमांत उपयोगिता प्रथम केला $\left(\mathrm{MU} _{\mathrm{n}}\right)$, सीमांत उपयोगिता द्वितीय केले $\left(\mathrm{MU} _{2}\right)$ और इसी प्रकार $\mathrm{n}^{\text {th }}$ इकाई तक का कुल योग है।

तालिका संख्या 2.1 तथा रेखाचित्र 2.1, एक वस्तु की विभिन्न मात्राओं के उपभोग से मिलने वाली सीमांत तथा कुल उपयोगिता के मूल्यों का एक काल्पनिक उदाहरण को दिखाती है। सामान्यतः यह देखा जाता है कि सीमांत उपयोगिता, वस्तु के उपयोग में वृद्धि के साथ गिर जाती है। ऐसा इसलिए होता है क्योंकि एक वस्तु की कुछ मात्रा उपलब्ध हो जाने पर, उपभोक्ता की उस वस्तु को और अधिक प्राप्त करने की इच्छा कम हो जाती है। तालिका तथा रेखाचित्र में इसी को दिखाया गया है।

देखिये, कि $\mathrm{MU} _{3} \mathrm{MU} _{2}$ से कम है। आप यह भी देख सकते हैं कि कुल उपयोगिता में वृद्धि होती है लेकिन घटती हुई दर पर। किसी वस्तु के उपयोग की मात्रा में परिवर्तन के फलस्वरूप, कुल उपयोगिता में वृद्धि की दर, उसकी सीमांत उपयोगिता की आय है। यह सीमांत उपयोगिता,

तालिका 2.1: एक वस्तु की विभिन्न मात्राओं के उपभोग से प्राप्त सीमांत तथा कुल उपयोगिता के मूल्य

वस्तु की उपभोग मात्रा में वृद्धि के साथ गिरती जाती है- 12 से 6,6 से 4 और इसी प्रकार आगे। यह निष्कर्ष, ह्रासमान उपयोगिता नियम से निकलता है। ह्वासमान उपयोगिता नियम बताता है कि जैसे-जैसे अन्य वस्तुओं के उपयोग को स्थिर रखते हुए किसी वस्तु के उपभोग को बढ़ाया जाता है, वस्तु को हर अगली इकाई के उपभोग से प्राप्त सीमांत उपयोगिता गिरती जाती है।

किसी वस्तु की विभिन्न मात्राओं के उपभोग से प्राप्त सीमांत एवं कुल उपयोगिता के मूल्य वस्तु के उपभोग में वृद्धि के साथ सीमान्त उपयोगिता घटती जाती है।

$\mathrm{MU}$ उस बिन्दू पर शून्य हो जाती है जब $\mathrm{TU}$ स्थिर रहता है। दिये गये उदाहरण में पाँचवों इकाई के उपभोग पर $\mathrm{TU}$ अपरिवर्तित रहती है, अतः $\mathrm{MU}_{5}=0$ इसके पश्चात $\mathrm{TU}$ गिरने लगाती है और $\mathrm{MU}$ ॠणात्मक हो जाती है।

एकल वस्तु की दशा में मांग वक्र की उत्पत्ति (ह्वासमान उपयोगिता नियम)

किसी वस्तु के मांग वक्र का, गणनावाचक विश्लेषण के द्वारा बनाया जा सकता है। मांग क्या है तथा मांग वक्र क्या है? वस्तु की मात्रा जिसे एक उपभोक्ता दिये गये वस्तु मूल्यों और आय पर, खरीदने के लिये इच्छुक एवं समर्थ है को उस वस्तु की मांग कहते हैं। वस्तु $\mathrm{X}$ की मांग, $\mathrm{X}$ वस्तु की स्वयं की कीमत के अतिरिक्त, अन्य वस्तुओं की कीमतों, (प्रतिस्थानापन्न एवं पूरक वस्तुएं 2.4 देखें), उपभोक्ता की रुचियों और वरीयता जैसे कारकों पर निर्भर करती है। मांग वक्र, एक वस्तु की, विभिन्न कीमतों पर, मांगे जाने वाली मात्राओं की रेखीय प्रस्तुति है। जो एक उपभोक्ता किसी वस्तु की विभिन्न कीमतों पर खरीदने के लिये इच्छुक है, अन्य संबंधित वस्तुओं की कीमतों को और उपभोक्ता की आय को स्थिर रखते हुए।

चित्र 2.2, एक व्यक्ति का वस्तु $\mathrm{X}$ के लिए, विभिन्न कीमतों पर, उसके काल्पनिक मांग वक्र को प्रदर्शित करता है। मात्राओं को क्षैतिज अक्ष पर तथा कीमतों को उर्ध्वाधर अक्ष पर दिखाया गया है।

वस्तु $X$ के लिए एक व्यक्तिगत का माँग वक्र

नीचे की ओर ढलवा मांग वक्र प्रदर्शित करता है कि नीचे मूल्यों पर एक व्यक्ति $\mathrm{X}$ वस्तु की अधिक मात्रा खरीदने को इच्छुक है तथा ऊँचे मूल्यों पर, वह वस्तु की कीमत तथा माँगें जाने वाली मात्रा के बीच ॠणात्मक संबंध है। इसे मांग का नियम कहते हैं।

नीचे की ओर ढलवा मांग वक्र की स्पष्टीकरण, ह्रासमान सीमांत उपयोगिता के विचार पर आधारित है। ह्वासमान सीमांत उपयोगिता का नियम बताता है कि वस्तु की प्रत्येक अगली इकाई, कम सीमांत उपयोगिता प्रदान करती है। इसलिये, व्यक्ति प्रत्येक अगली इकाई के लिये उतना देने के लिये इच्छुक नहीं होगा और इसी कारण मांग वक्र नीचे की ओर ढलवा वक्र होता है। $\mathrm{X}$ वस्तु की रू. 40 प्रति इकाई कीमत पर, व्यक्ति की $\mathrm{x}$ वस्तु की पांच इकाइयों की मांग थी। वस्तु की छठवीं इकाई, पांचवी इकाई से कम महत्व की होगी। व्यक्ति छठी इकाई को तभी खरीदेगा जब कीमत रू. 40 प्रति इकाई से नीचे गिर जाए। अतः हासमान सीमांत उपयोगिता नियम, यह स्पष्ट करता है कि मांग वक्रों का ॠणात्मक दाम क्यों होता हैं।

2.1.2 क्रमवाचक उपयोगिता विश्लेषण

गणनावाचक उपयोगिता विश्लेषण समझने में सरल है, लेकिन उपयोगिता का संख्याओं के रूप में परिमाणन, इसका एक बड़ा दोष है। वास्तविक जीवन में, हम उपयोगिता को संख्याओं के रूप में कभी व्यक्त नहीं करते। अधिक से अधिक हम कम या अधिक उपयोगिता के आधार पर क्रम दे सकते हैं। दूसरे शब्दों में, उपभोक्ता उपयोगिता को संख्याओं में नहीं मापता है, यद्यपि वह विभिन्न उपभोक्ता बंडलों को क्रम देता है। यही, क्रमवाचक उपयोगिता विश्लेषण प्रसंग का प्रारंभिक बिन्दु है।

बंडलो के सेट में एक उपभोक्ता के अभिमानों को चित्र द्वारा भी प्रदर्शित किया जा सकता है। हम पहले ही देख चुके हैं, कि एक उपभोक्ता का उपलब्ध बंडलों को एक द्वितीय चित्र द्वारा दिखाया जा सकता है। बिन्दुओं जो उपभोक्ता का समान उपयोगिता है, प्रदान करने वाले बंडलों का प्रतिनिधित्व करते हैं, को रेखाचित्र 2.3 में दिखाये गये वक्र को प्राप्त करने के लिये सामान्यतः जोड़ा जा सकता है।

अनधिमान वक्र- एक अनधिमान वक्र उन सभी बिन्दुओं का प्रतिनिधित्व करने वाले बंडलो को जिनको उपभोक्ता तटस्थ समझाता है और उन्ही को जोड़ता है।

एक अनधिमान वक्र पर सभी बिन्दु जैसे $\mathrm{A}, \mathrm{B}$, $\mathrm{C}$ तथा $\mathrm{D}$ उपभोक्ता को समान स्तर का संतोष प्रदान करते हैं। यह स्पष्ट है कि जब उपभोक्ता को एक और केला प्राप्त होता है तो उसको कुछ आमों का त्याग करना पड़ता है ताकि उसकी उपयोगिता का स्तर वही रहे और वह उसी अनधिमान वक्र पर रहे।

एक अतिरिक्त केला प्राप्त करने के लिये, कुल उपयोगिता का स्तर समान रहते हुए, आमों की वह मात्रा, जिसका उपभोक्ता को त्याग करना पड़ता है, सीमांत प्रतिस्थापन दर कहते हैं। दूसरे शब्दों में, MRS, सरलरूप में वह दर है जिस पर उपभोक्ता आमों के स्थान पर केलों को प्रतिस्थापित करेगा। ताकि उसकी उपयोगिता समान रहे। अतः $M R S=|\Delta Y / \Delta X|^{3}$

तालिका 2.2: ह्रासमान सीमांत प्रतिस्थापना दर के नियम का प्रदर्शन

आप देख सकते हैं कि उपरोक्त तालिका में, जैसे हम केलों की संख्या को बढ़ाते हैं, केले की प्रत्येक अतिरिक्त इकाई के लिये त्याग किये जाने वाले आमों की मात्रा गिरती जाती है। अन्य शब्दों में, केलों की संख्या में वृद्धि के साथ MRS कम हो जाता है। उपभोक्ता के पास जैसे-जैसे केलों की संख्या बढ़ती है केले से प्राप्त MU गिरती जाती है। इसी भांति, आमों की संख्या में कमी से, आमों से प्राप्त सीमांत उपयोगिता बढ़ती जाती है। इस प्रकार, केलों की संख्या में वृद्धि होने से, उपभोक्ता की, कम और कम, आमों की मात्रा त्यागने की प्रवृति बढ़ेगी। केलों की मात्रा में वृद्धि के फलस्वरूप, MRS के गिरने की इस प्रवृति को, ह्रासमान सीमांत प्रतिस्थापना का नियम कहते हैं। इसे चित्र 2.3 में देखा जा सकता है। । $\mathrm{A}$ बिन्दु से $\mathrm{B}$ बिन्दु पर जाने में, उपभोक्ता 3 आमों का त्याग करता है, $\mathrm{B}$ बिन्दु से $\mathrm{C}$ बिन्दु पर जाने में, वह 2 आमों का त्याग करता है तथा $\mathrm{C}$ बिन्दु से $\mathrm{D}$ बिन्दु पर जाने में, वह एक आम का त्याग करता है। अतः यह स्पष्ट है कि प्रत्येक अगले क्रेता के लिये उपभोक्ता थोड़ी और थोड़ी, आमों की मात्रा का त्याग करता है।

अनधिमान वक्र की आकृति

उल्लेखनीय है, कि ह्रासमान सीमांत प्रतिस्थान का नियम, अनधिमान वक्र को उदूगम के प्रति उत्तल बना देता है, (क्यों? एक अनधिमान वक्र बनाकर इसकी जाँच कीजिये)। एक अनधिमान वक्र की यह अति सामान्य आकृति है। लेकिन पूर्ण स्थापन्न वस्तुओं में सीमांत प्रतिस्थापन्न दर नहीं गिरती है, यह समान रहती है। एक उदाहरण लेते हैं-

तालिका 2.3: ह्रासमान सीमांत प्रतिस्थापन दर का प्रदर्शन

यहां, इन सभी संयोगों के बीच, जब तक की पाँच रुपये के सिक्के तथा पाँच रुपये के नोटों का योग वही रहता है, उपभोक्ता तटस्थ है। उपभोक्ता के लिये, इससे कोई फर्क नहीं पड़ता कि उसे पाँच रुपये का एक सिक्का मिले अथवा पांच रुपये का एक नोट। इसलिये, इस बात का विचार किये बिना कि उसके पास पाँच रुपये के कितने नोट हैं, उपभोक्ता, पाँच रुपये के एक नोट के “सही विकल्प उन वस्तुओं के लिये है, जो एक दूसरे के स्थान पर प्रयोग किया जा सकता हे और उपभोक्ता को उसी तरह की उपयोगिता प्रदान करता है।

बदले, केवल एक पाँच रुपये का सिक्का त्याग करेगा। इसलिये उपभोक्ता के लिये यह दोनों वस्तुएं पूर्ण प्रतिस्थापन्न हैं और इनको प्रदर्शित करने वाला अनधिमान वक्र एक सीधी रेखा होगी।

पूर्ण प्रतिस्थापन्न के लिए अनधिमान वक्र: दो वस्तुओं का अनधिमान वक्र जो पूर्ण स्थानापन्न होती हैं, एक सीधी रेखा होती है।

चित्र 2.4 में यह देखा जा सकता है कि उपभोक्ता उतने ही पाँच रुपये के सिक्कों का त्याग करता है जब प्रत्येक बार उसके पास अतिरिक्त पाँच रुपये का नोट होता है। पूर्ण प्रतिस्थापन्न वस्तुओं का अनधिमान वक्र दो पूर्ण स्थापन्न वस्तुओं को प्रदर्शित करने वाली दो वस्तुओं की अनधिमान एक सीधी रेखा होती है।

एकदिष्ट अधिमान

उपभोक्ता अधिमानों के विषय में यह मान लिया जाता है कि अगर किन्हों दो बंडलों $\left(x_{1}, x_{2}\right)$ और $\left(y_{1}, y_{2}\right)$ में $\left(x_{1}, x_{2}\right)$ बंडल में कम से कम एक वस्तु हो और $\left(y_{1}, y_{2}\right)$ की तुलना में अन्य वस्तु की कम मात्रा न हो, तो उपभोक्ता $\left(y_{1}, y_{2}\right)$ के बजाए $\left(x_{1}, x_{2}\right)$ को अधिमान देता है। अधिमानों के इस प्रकार को एकदिष्ट अधिमान कहा जाता है, यदि उपभोक्ता किन्हीं दो बंडलों में से उस बंडल को अधिमान देता है जिसे इन वस्तुओं में से कम-से-कम एक वस्तु की अधिक मात्रा हो और दूसरे बंडल की तुलना में दूसरी वस्तु की भी कम मात्रा न हो।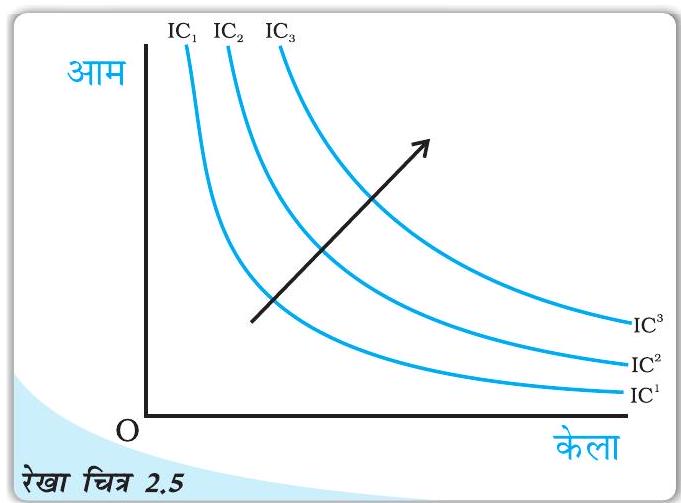

अनधिमान मानचित्र: अनधिमान वक्रों का एक परिवार ‘तीर’ दिखाता है कि उच्च अनधिमान वक्र पर बंडल, नीचे अनधिमान वक्र पर बंडलों की अपेक्षा पसंद किये जाते हैं।

अनधिमान मानचित्र

सभी बंडलों पर उपभोक्ता के अधिमानों को अनधिमान वक्र-समूहों द्वारा दर्शाया जा सकता है, जैसा कि रेखाचित्र 2.5 में दर्शाया गया है। इसे उपभोक्ता का अनधिमान मानचित्र कहते हैं। अनधिमान वक्र पर स्थित सभी बिन्दु उन बंडलों का प्रतिनिधित्व करते हैं जिन्हें उपभोक्ता तटस्थ मानता है। अधिमानों की एकदिष्टता का यह अभिप्राय है कि किन्हीं दो अनधिमान वक्रों के बीच ऊपर वाले बंडलों पर स्थित बंडलों को नीचे वाले वक्र पर स्थित बंडलों की अपेक्षा अधिमानता दी जाती है।

अनधिमान वक्रों के लक्षण/विशेषताएँ

1. अनधिमान वक्र दाएं से बाएं नीचे की ओर ढलवा होते हैं-

एक अनधिमान वक्र दाएं से बाएं नीचे की ओर ढलवा होता है जिसका अर्थ है कि अधिक $\mathrm{X}$ वस्तु प्राप्त करने के लिये, उपभोक्ता को $\mathrm{Y}$ वस्तु की कुछ मात्रा का त्याग करना पड़ता है। यदि उपभोक्ता $\mathrm{Y}$ वस्तु की कुछ मात्रा का, $\mathrm{X}$ वस्तु की मात्रा में वृद्धि होने पर, त्याग नहीं करता है तो इसका यह अर्थ होगा कि उपभोक्ता, $\mathrm{Y}$ की वस्तु वही अथवा अधिक मात्रा, $\mathrm{X}$ वस्तु के बदले प्राप्त करता है, और वह एक उच्च अनधिमान वक्र पर चला जाता है। अतः जब तक उपभोक्ता उसी अनधिमान वक्र पर स्थित है, केलों में वृद्धि को, आमों की मात्रा कम करके क्षतिपूर्ति की जानी चाहिये।

2. उच्च अनधिमान वक्र, उपयोगिता के उच्च स्तर को प्रदान करता है:

जब तक एक वस्तु की सीमांत उपयोगिता धनात्मक होती है, तब एक व्यक्ति सदैव ही उस वस्तु की अधिक मात्रा प्राप्त करना चाहेगा, क्योंकि वस्तु की अधिक मात्रा, संतोष के स्तर को बढ़ायेगी।

केले और आम के तीन विभिन्न संयोगों - A, $\mathrm{B}$ तथा $\mathrm{C}$ को देखिये जिन्हें तालिका 2.4 . और रेखाचित्र 2.7 में दिखाया गया हैं।

अनधिमान वक्र का ढ़ालः अनधिमान वक्र नीचे की ओर ढलवा होते हैं। अनधिमान वक्र केलों की मात्रा में वृद्धि, आमों की घटती हुई मात्राएं जुड़ी हुई हैं। यदि $\Delta x_{1}>0$

तालिका 2.4: उपयोगिता के विभिन्न स्तरों का प्रतिनिधित्व वस्तु के विभिन्न संयोजनों के रूप में होता है

संयोगों A, B तथा $\mathrm{C}$ में, आमों की समान मात्रा है, पस्तु केलों की मात्रा भिन्न हैं। संयोग $\mathrm{B}, \mathrm{A}$ को अपेक्षा उपयोगिता का उच्च स्तर प्रदान करेगा। इसलिये $\mathrm{B}, \mathrm{A}$ की अपेक्षा एक ऊँचे अनधिमान वक्र पर होगा, अधिक संतोष को व्यक्त करेगा। इसी भांति $\mathrm{C}$ में $\mathrm{B}$ की अपेक्षा अधिक केले है ( $\mathrm{B}$ और $\mathrm{C}$ दोनों में आमों की मात्रा समान है), इसलिये $\mathrm{C}, \mathrm{B}$ की अपेक्षा संतोष के उच्च स्तर को प्रदान करेगा और $\mathrm{B}$ की अपेक्षा, एक और ऊँचे अधिमान वक्र पर होगा।

सभी उच्च अनधिमान वक्र, उपयोगिता के उच्च स्तर को प्रदान करता हैं।

अधिक आम अथवा अधिक केले अथवा दोनों की अधिक मात्रा वाले संयोग, उच्च अनधिमान वक्र पर होंगे तथा उन संयोगों का प्रतिनिधित्व करेंगे जो संतोष के उच्च स्तर को प्रदान करेंगे।

3. दो अनधिमान वक्र कभी एक दूसरे को नहीं काटते हैं:

एक दूसरे को काटते हुए दो अनधिमान वक्र, परस्पर विरोधी परिणामों को दिखायेंगे। इसे समझने के लिये, हम चित्र 2.8 में दो अनधिमान वक्रों को एक दूसरे को काटने देते हैं। क्योंकि बिन्दु $\mathrm{A}$ तथा $\mathrm{B}$, एक ही अनधिमान वक्र $\mathrm{IC} _{1}$ पर स्थित हैं, संयोग $\mathrm{A}$ तथा $\mathrm{B}$ से समान संतोष का स्तर प्राप्त होगा। इसी प्रकार बिन्दु $\mathrm{B}$ तथा $\mathrm{C}$, एक ही अनधिमान वक्र $\mathrm{IC} _{2}$ पर स्थित हैं, संयोग $\mathrm{B}$ तथा $\mathrm{C}$ समान संतोष का स्तर प्रदान करेंगे।

इससे यह निष्कर्ष निकलता है, कि बिन्दु B तथा $\mathrm{C}$ से भी प्राप्त उपयोगिता समान है। लेकिन यह स्पष्ट है कि विसंगत निष्कर्ष है, क्योंकि केलों की उसी मात्रा से, जैसा बिन्दु $\mathrm{B}$ पर, उपभोक्ता आमों की अधिक मात्रा प्रदान करता है। इस प्रकार बिन्दु $\mathrm{B}$ पर, उपभोक्ता बिन्दु $\mathrm{C}$ की अपेक्षा अधिक अच्छी स्थिति में है। अतः एक दूसरे को काटते हुए अनधिमान वक्र, विसंगत निष्कर्ष प्राप्त करते हैं। अतः दो अनधिमान वक्र एक दूसरे को नहीं काट सकते।

रेखाचित्र 2.8

दो अनधिमान वक्र कभी एक दूसरे को नहीं काटते हैं।

2.2 उपभोक्ता का बजट

मान लीजिए किसी उपभोक्ता के पास केवल एक निश्चित मात्रा में पैसे (आय) ऐसी दो वस्तुओं पर व्यय करने के लिए हैं, जिनकी लागत बाज़ार में दी गयी हैं। उपभोक्ता दोनों वस्तुओं की अलग-अलग या मिली-जुली ऐसी मात्रा को नहीं खरीद सकता, जिनका वह उपभोग करना चाहता है। उपभोक्ता के लिए उपलब्ध उपभोग बंडल दोनों वस्तुओं की कीमत तथा उपभोक्ता की आय पर निर्भर करता है। निश्चित आय तथा दोनों वस्तुओं की कीमतों को देखते हुए उपभोक्ता केवल उन्हीं बंडलों को खरीद सकता है जिनका मूल्य उसकी आय से कम हो या बराबर हो।

2.2.1 बजट सेट एवं बजट रेखा

मान लीजिए उपभोक्ता की आय $M$ है तथा दोनों वस्तुओं की कीमतें क्रमशः $p_{1}$ तथा $p_{2}$ हैं। यदि उपभोक्ता केले की $x_{1}$ इकाइयाँ खरीदना चाहता है तो उसे कुल मिलाकर $p_{1} x_{1}$ धन व्यय करना पड़ेगा। इसी प्रकार से, अगर उपभोक्ता आम की $x_{2}$ इकाइयाँ खरीदना चाहता है, तो उसे $p_{2} x_{2}$ धन व्यय करना होगा। इसलिए यदि उपभोक्ता केले की $x_{1}$ इकाइयों और आम की $x_{2}$ इकाइयों का बंडल खरीदना चाहता है, तो उसे $p_{1} x_{1}+p_{2} x_{2}$ धन राशि व्यय करनी होगी। वह यह बंडल तभी खरीद पायेगी, जब उसके पास कम-से-कम $p_{1} x_{1}+p_{2} x_{2}$ धन राशि हो। वस्तुओं की विद्यमान कीमतों तथा अपनी आय के अनुसार उपभोक्ता ऐसा कोई भी बंडल उसी सीमा तक खरीद सकता है, जब तक उसकी कीमत उसकी आय के बराबर या उससे कम रहे। दूसरे शब्दों में, उपभोक्ता कोई $\left(x_{1} x_{2}\right)$ बंडल निम्न स्थिति में खरीद सकता है:

$$ \begin{equation*} p_{1} x_{1}+p_{2} x_{2} \leq M \tag{2.1} \end{equation*} $$

यह असमानता (2.1) उपभोक्ता का बजट प्रतिबंध कहलाती है। उपभोक्ता के लिए उपलब्ध बंडलों के सेट को बजट सेट कहा जाता है। इस प्रकार, बजट सेट उन सभी बंडलों का संग्रह है, जिसे उपभोक्ता विद्यमान बाज़ार कीमतों पर अपनी आय से खरीद सकता है।

उदाहरण 2.1

एक ऐसे उपभोक्ता का उदाहरण लें, जिसके पास 20 रुपए हैं तथा मान लीजिए दोनों वस्तुओं की लागत 5 रुपए रखी गयी है और ये समाकलित इकाइयों के रूप में ही उपलब्ध हैं। जो बंडल उपभोक्ता खरीद सकता है, वे हैं: $(0,0),(0,1),(0,2),(0,3),(0,4),(1,0)$, $(1,1),(1,2),(1,3),(2,0),(2,1),(2,2),(3,0),(3,1)$ तथा $(4,0)$ । इन बंडलों में से $(0,4),(1,3),(2,2),(3,1)$ तथा $(4,0)$ की लागत ठीक 20 रुपए है तथा अन्य बंडलों की लागत 20 रुपए से कम है। उपभोक्ता $(3,3)$ तथा $(4,5)$ बंडलों को खरीद नहीं सकता, क्योंकि प्रचलित लागतों पर उनकी कीमत 20 रुपए से अधिक है।

यदि दोनों वस्तुएँ पूर्णतः विभाज्य ${ }^{6}$ हों तो उपभोक्ता के बजट सेट में सभी बंडल $\left(x_{1} x_{2}\right)$ समाहित होंगे, जबकि $x_{1}$ तथा $x_{2}$ ऐसी संख्याएँ हैं जो शून्य $(0)$ और $p_{1} x_{1}+p_{2} x_{2} \leq M$ से बड़ी या उसके बराबर है। इस बजट सेट को रेखाचित्र 2.1 में एक आरेख के द्वारा दर्शाया गया है।

धनात्मक चतुर्थांश के वे सभी बंडल जो रेखा के नीचे या उस पर स्थित हैं, बजट सेट में शामिल हैं। रेखा का समीकरण है:

$$ \begin{equation*} p_{1} x_{1}+p_{2} x_{2}=M \tag{2.2} \end{equation*} $$

इस रेखा में वे सभी बंडल शामिल हैं, जिनकी लागत $M$ के बराबर है। यह रेखा बजट रेखा कहलाती है। बजट रेखा के नीचे के बिन्दु उन बंडलों को प्रदर्शित करते हैं, जिनका लागत $M$ से बिल्कुल कम हो।

बजट सेट: केले की मात्रा क्षैतिज अक्ष तथा आम की मात्रा उर्ध्वाधर अक्ष पर मापी जा रही है। इस आरेख में कोई भी बिन्दु दोनों वस्तुओं के एक बंडल को प्रदर्शित करता है। इस बजट सेट में दर्शायी गई सीधी रेखा के ऊपर या नीचे स्थित सभी बिन्दु आ जाते हैं। इसका समीकरण है: $p_{1} x_{1}+p_{2} x_{2}=M$.

समीकरण (2.2) को इस प्रकार भी लिखा जा सकता है।

$$ \begin{equation*} x_{2}=\frac{M}{p_{2}}-\frac{p_{1}}{p_{2}} x_{1} \tag{2.3} \end{equation*} $$

बजट रेखा एक सीधी रेखा है जिसका समस्तरीय अंतःखंड $\frac{M}{p_{1}}$ तथा उर्ध्वाधर अंतःखंड $\frac{M}{p_{2}}$ है। समस्तरीय अंतःखंड उस बंडल का प्रतिनिधित्व करता है जिसको उपभोक्ता उसी स्थिति में खरीद सकता है, यदि वह अपनी सारी आय केले पर व्यय कर दे। इसी तरह उर्ध्वाधर अंतःखंड उस बंडल का प्रतिनिधित्व करता है जिसे उपभोक्ता उस स्थिति में खरीद सकता है, जब वह अपनी सारी आय आम पर व्यय कर दे। बजट रेखा की प्रवणता है $-\frac{p_{1}}{p_{2}}$

मूल्य अनुपात तथा बजट रेखा की प्रवणता

बजट रेखा पर किसी भी बिन्दु के विषय में सोचिए। यह बिन्दु एक ऐसे बंडल को दर्शाता है, जिस पर उपभोक्ता का पूरा बजट व्यय हो जाता है। मान लीजिए कि अब उपभोक्ता केले की 1 इकाई अधिक लेना चाहता है, तब वह ऐसा तभी कर सकता है जब वह दूसरी वस्तु की कुछ मात्रा को छोड़ दे। यदि उसे केले की एक अतिरिक्त इकाई की चाहत है, तो उसे आम की कितनी मात्रा छोड़नी पड़ेगी? यह दोनों वस्तुओं की कीमतों पर निर्भर करेगा। केले की एक इकाई का लागत $p_{1}$ है। अतः उसे आम पर $p_{1}$ मात्रा के बराबर अपना व्यय घटाना पड़ेगा। $p_{1}$ से वह वस्तु 2 की $\frac{p_{1}}{p_{2}}$ इकाइयाँ खरीद सकता है। अतः यदि उपभोक्ता केले की एक अतिरिक्त इकाई चाहती है और वह अपनी संपूर्ण आय को व्यय करती है, तो उसे आम की $\frac{p_{1}}{p_{2}}$ इकाइयाँ छोड़नी पड़ेंगी। दूसरे शब्दों में, दी गई बाज़ार की स्थितियों में उपभोक्ता वस्तु 1 को वस्तु 2 की जगह $\frac{p_{1}}{p_{2}}$ की दर पर प्रतिस्थापित कर सकता है। बजट रेखा की प्रवणता का निरपेक्ष मूल्य ${ }^{8}$ उस दर को मापती है जिस पर उपभोक्ता आम के बदले केले खरीदती है, जब वह अपना संपूर्ण बजट खर्च कर देती है।

बजट रेखा की प्रवणता की व्युत्पत्ति

बजट रेखा की प्रवणता पूरी बजट रेखा पर केले के प्रति इकाई परिवर्तन की स्थिति में आम में हुए परिवर्तन की मात्रा का मापन करती है। बजट रेखा पर किन्हीं दो बिन्दुओं $\left(x_{1} x_{2}\r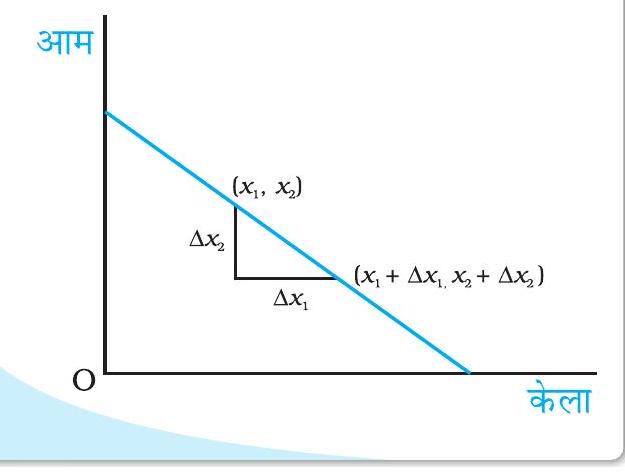ight)$ तथा $\left(x_{1}+\Delta x_{1}, x_{2}+\Delta x_{2}\right)$ पर विचार करें:

ऐसी स्थिति में,

$$\begin{equation*} p_{1} x_{1}+p_{2} x_{2}=M \tag{2.4} \end{equation*}$$

तथा $$\begin{equation*}p_{1}\left(x_{1}+\Delta x_{1}\right)+p_{2}\left(x_{2}+\Delta x_{2}\right) =M \tag{2.5}\end{equation*}$$
(2.5) में से (2.4) को घटाने पर

$$\begin{equation*} p_{1} \Delta x_{1}+p_{2} \Delta x_{2}=0 \tag{2.6} \end{equation*} $$

(2.6) में पदों का पुनर्योजन करके हमें प्राप्त होता है

$$ \begin{equation*} \frac{\Delta x_{2}}{\Delta x_{1}}=-\frac{p_{1}}{p_{2}} \tag{2.7} \end{equation*}$$

2.2.2 बजट सेट में बदलाव

उपलब्ध बंडलों का सेट दोनों वस्तुओं की कीमत तथा उपभोक्ता की आय पर निर्भर करता है। जब दोनों में से किसी भी वस्तु की कीमत अथवा उपभोक्ता की आय बदलती है, तो उपलब्ध बंडल का सेट भी बदल सकता है। मान लीजिए कि उपभोक्ता की आय $M$ से बदल कर $M^{\prime}$ हो जाती है, परन्तु दोनों वस्तुओं की कीमतें नहीं बदलतीं। नई आय होने पर उपभोक्ता सभी बंडल $\left(x_{1}, x_{2}\right)$ खरीद सकता है, जिसके होने पर $p_{1} x_{1}+p_{2} x_{2} \leq M^{\prime}$ अब बजट रेखा का समीकरण है

$$ \begin{equation*} p_{1} x_{1}+p_{2} x_{2}=M^{\prime} \tag{2.8} \end{equation*} $$

समीकरण (2.8) निम्न रूप में भी लिखा जा सकता है

$$ \begin{equation*} x_{2}=\frac{M^{\prime}}{p_{2}}-\frac{p_{1}}{p_{2}} x_{1} \tag{2.9} \end{equation*} $$

ध्यान दीजिए कि नई बजट रेखा की प्रवणता वही है जो उपभोक्ता की आय में परिवर्तन होने से पहले की बजट रेखा की प्रवणता थी। तथापि, आय में बदलाव के बाद ऊर्ध्वाधर अंतःखंड बदल गया है। यदि आय में वृद्धि होती है, अर्थात् यदि $M^{\prime}>M$, तब ऊर्ध्वाधर अंतःखंड बढ़ता है बजट रेखा के समानांतर बाहय विस्थापन होता है। यदि आय बढ़ती है, तो उपभोक्ता विद्यमान बाज़ार कीमतों पर अधिक वस्तुएँ खरीद सकता है। इसी प्रकार, यदि आय घटती है, अर्थात् यदि $M^{\prime}<M$, तो ऊर्ध्वाधर अंतःखंड घटता है तथा इस प्रकार बजट रेखा में समानांतर आवक स्थानापन्न होता है। यदि आय कम होती है, तो वस्तुओं की उपलब्धता भी घटती जाती है। दोनों वस्तुओं की कीमतें समान रहने पर उपभोक्ता की आय में बदलाव के परिणामस्वरूप उपलब्ध बंडलों में होने वाले परिवर्तनों को रेखाचित्र 2.10 में दर्शाया गया है।

वस्तुओं के उपलन्ध बंडल के सेट में वह बदलाव जो उपभोक्ता की आय में बदलावों के परिणास्वरूप होता है: आय में कमी हो जाने से बजट रेखा में समानांतर आवक स्थानापन्न होता है, जैसा कि पैनल (a) में है। आय में वृद्धि से बजट रेखा में समांनातर जावक शिफ्ट होता है, जैसा कि पैनल (b) में हैं।

अब मान लीजिए, कि वस्तु 1 का कीमत $p_{1}$ से बदलकर $p_{1}^{\prime}$ हो जाती है, परन्तु वस्तु 2 की कीमत तथा उपभोक्ता की आय नहीं बदलती। अब वस्तु 1 की नई कीमत पर उपभोक्ता सभी बंडल $\left(x_{1} x_{2}\right)$ खरीद सकता है अर्थात् $p_{1}^{\prime} x_{1}+p_{2} x_{2} \leq M$ बजट रेखा का समीकरण होगा।

$$ \begin{equation*} p_{1}^{\prime} x_{1}+p_{2} x_{2}=M \tag{2.10} \end{equation*} $$

समीकरण (2.10) को निम्न रूप में भी लिखा जा सकता है

$$ \begin{equation*} x_{2}=\frac{M}{p_{2}}-\frac{p_{1}^{\prime}}{p_{2}} x_{1} \tag{2.11} \end{equation*} $$

ध्यान दीजिए कि नई बजट रेखा का ऊर्ध्वाधर अंतःखंड वैसा ही है, जैसा कि केले की कीमत में बदलाव आने से पहले बजट रेखा के ऊर्ध्वाधर अंतःखंड का था। किन्तु, बजट रेखा की प्रवणता तथा क्षैतिज अंतःखंड, कीमत में बदलाव के पश्चात बदल गयी है। यदि केला की कीमत बढ़ती है, अर्थात् यदि $p^{\prime}>p_{1}$ तो बजट रेखा की प्रवणता का निरपेक्ष मूल्य बढ़ता जाता है और इस प्रकार बजट रेखा अधिक प्रवण हो जाती है (यह ऊध्र्वाधर अंतःखंड के आस-पास आवक की ओर हो जाती है तथा क्षैतिजीय अंतःखंड गिर जाता है)। यदि केले की कीमत घटती है अर्थात् $p_{1}^{\prime}<p_{1}$, बजट रेखा की प्रवणता का निरपेक्ष मूल्य घटता है तथा इस प्रकार बजट रेखा अधिक सपाट हो जाती है (यह उर्ध्वाधर अंतःखंड के आस-पास जावक की ओर हो जाती है तथा क्षैतिजीय अंतःखंड बढ़ जाता है)। केले की कीमत में बदलाव के परिणामस्वरूप उपलब्ध बंडल के सेट में बदलाव, जबकि आम की कीमत तथा उपभोक्ता की आय समान रहती है। रेखाचित्र 2.11 में दर्शाया गया है।

वस्तुओं के उपलब्ध बंडलों के सेट में बदलाव के परिणामस्वरूप केले की कीमत में बदलावः केले की कीमत में वृद्धि बजट रेखा को अधिक प्रवण बना देती है जैसा कि पैनल (a) में दर्शाया गया है। केले की कीमत में कमी बजट रेखा को अधिक सपाट बना देती है, जैसा कि पैनल (b) में दर्शाया गया है।

2.3 उपभोक्ता का इष्टतम चयन

बजट सेट में वे सभी बंडल शामिल हैं, जो कि उपभोक्ता के लिए उपलब्ध होते हैं। उपभोक्ता अपने बजट सेट में से उपभोग बंडल का चयन कर सकता है। परन्तु वह उपलब्ध बंडलों में से अपने लिए उपभोग बंडल का चयन किस आधार पर करता है? अर्थशास्त्र में यह मान लिया जाता हे कि उपभोक्ता उपलब्ध सभी बंडलों में से अपने उपभोग बंडल का चयन अपनी रुचि तथा अधिमान के अनुसार बजट सेट के बंडलों के आधार पर करता है। यह सामान्य रूप से मान लिया जाता है कि उपभोक्ता के पास सभी बंडलों के सेट के विषय में अच्छी तरह स्पष्ट अधिमान हैं। वह किन्हीं दो बंडलों की तुलना कर सकती है। दूसरे शब्दों में, वह दो बंडलों में से किसी एक को अधिमान दे सकता है या तटस्थ रहता है।

पिछले दो भागों में, हमने उपभोक्ता के लिए उपलब्ध बंडलों के सेट के विषय में चर्चा की थी और उसके इन बंडलों की अधिमानता के विषय में भी बताया था कि किस बंडल का वह चुनाव करती है? अर्थशास्त्र में साधारणतः यह मान लिया जाता है कि उपभोक्ता युक्तिशील व्यक्ति होता है। युक्तिशील व्यक्ति को स्पष्टतः यह जानकारी होती है कि उसके लिए क्या अच्छा और क्या बुरा, तथा किसी भी दी हुई स्थिति में वह सदा इसका प्रयास करता है कि अपने लिए सबसे अच्छे को ही प्राप्त करे। अतः उपलब्ध बंडलों के सेट के लिए न केवल एक उपभोक्ता के पास सुस्पष्ट अधिमान होता है, अपितु वह अपने अधिमानों के अनुसार कार्यवाई भी करता है। युक्तिशील उपभोक्ता अपने लिए उपलब्ध बंडलों में से सदा वही बंडल चुनता है, जिसे वह सर्वाधिक अधिमानता देता है।

पिछले भागों में यह देखा गया था कि बजट सेट उन बंडलों के बारे में बताता है, जो उपभोक्ता को उपलब्ध हैं तथा उपलब्ध बंडलों के बारे में उसके अधिमान प्रायः अनधिमान मानचित्र द्वारा प्रदर्शित किए जा सकते हैं। अतः उपभोक्ता की समस्या को निम्न रूप में भी वर्णित किया जा सकता है; युक्तिशील उपभोक्ता की समस्या यह होती है कि वह अपने उपलब्ध बजट सेट को देखते हुए संभावित उच्चतम अनधिमान वक्र के बिन्दु पर कैसे पहुँचे।

विस्थापन की सीमांत दर तथा कीमतों के अनुपात में समानता

उपभोक्ता का इष्टतम बंडल ऐसे बिन्दु पर स्थित होता है, जहाँ बजट रेखा किसी एक अनधिमान वक्र को स्पर्श करती है। यदि बजट रेखा अनधिमान वक्र के किसी बिन्दु को स्पर्श करती हो, तो अनधिमान वक्र की प्रवणता का निरपेक्ष कीमत और बजट रेखा (कीमत अनुपात) का निरपेक्ष कीमत उस बिन्दु पर एक समान होंगे। हम पहले यह विचार कर चुके हैं कि अनधिमान वक्र की प्रवणता उस दर को व्यक्त करती है, जिस पर उपभोक्ता एक वस्तु के स्थान पर दूसरी वस्तु को लेने के लिए तैयार है। बजट रेखा की प्रवणता वह दर है, जिस पर उपभोक्ता बाज़ार में एक वस्तु के स्थान पर दूसरी वस्तु को लेने में सक्षम होता है। इष्टतम बिन्दु पर दोनों दर एक जैसी होनी चाहिए। इसका कारण जानने के लिए एक ऐसे बिन्दु को लें, जहाँ ऐसा नहीं है। मान लीजिए, ऐसे बिन्दु पर प्रतिस्थापन की सीमांत दर 2 है और यह भी मानते हैं कि दोनों वस्तुओं की कीमत एक जैसी है। इस बिन्दु पर यदि उपभोक्ता को केले की एक अतिरिक्त इकाई दे दी जाए, तो वह उसके बदले आम की दो इकाइयाँ छोड़ देने के लिए तैयार है। लेकिन, वह बाज़ार में आम की केवल एक इकाई देकर ही केले की एक अतिरिक्त इकाई खरीद सकती है। इसलिए, अगर वह केले की एक अतिरिक्त इकाई खरीद लेती है, तो वह इस बिन्दु द्वारा प्रदर्शित बंडल की तुलना में दोनों वस्तुओं की अधिक मात्रा प्राप्त कर सकती है और इस प्रकार अपने अधिमानित बंडल को प्राप्त करने की ओर प्रवृत्त हो सकती है। अतः जिस बिन्दु पर विस्थापन की सीमांत दर अधिक हो, तो कीमत अनुपात इष्टतम बिन्दु नहीं ले सकता। विस्थापन की सीमांत दर जिस-जिस बिन्दु पर कीमत अनुपात से कम हो उसके विषय में ही तर्क स्वीकार किया जा सकता है।

यदि ऐसा बिन्दु कोई है, तो वह कहाँ स्थित होगा? इष्टतम बिन्दु बजट रेखा पर स्थित होगा। बजट रेखा से नीचे स्थित बिन्दु इष्टतम नहीं हो सकता। बजट रेखा से नीचे स्थित बिन्दु की तुलना में बजट रेखा पर हमेशा कोई ऐसा बिन्दु होता है, जिसमें दोनों वस्तुओं में से कम से कम एक की मात्रा अधिक होती है तथा दूसरी की मात्रा भी कम नहीं होती अतः उपभोक्ता एकदिष्ट अधिमानों वाले इसी बिन्दु को अधिमानता देता है। अतः यदि उपभोक्ता के अधिमान एकदिष्ट हों तो बजट रेखा से नीचे किसी भी बिन्दु पर कोई ऐसा बिन्दु होता है, जिसे उपभोक्ता अधिमानता देता है। बजट रेखा के ऊपर स्थित बिन्दु उपभोक्ता को उपलब्ध नहीं होते। इसलिए, उपभोक्ता का इष्टतम बंडल (सबसे अधिक अधिमान वाला बंडल) बजट रेखा पर स्थित होता है।

बजट रेखा पर इष्टतम बंडल कहाँ स्थित होगा? जिस बिन्दु पर बजट रेखा केवल अनधिमान वक्रों में से किसी एक को स्पर्श करती है, वही इष्टतम ${ }^{9}$ होगा। यह देखने के लिए कि ऐसा क्यों है, ध्यान दीजिए कि बजट रेखा पर कोई भी बिन्दु (उस बिन्दु को छोड़कर जिस पर वह अनधिमान वक्र को छूता है) किसी नीचे वाले अनधिमान वक्र पर स्थित होता है और इस प्रकार निम्नस्तरीय होता है। अतः, ऐसा एक बिन्दु उपभोक्ता का इष्टतम नहीं हो सकता। इष्टतम बंडल बजट रेखा के ऐसे बिन्दु पर स्थित होता है, जहाँ बजट रेखा अनधिमान वक्र पर स्पर्श रेखीय हो।

उपभोक्ता का इष्टतम बिन्दुः बिन्दु $\left(x _{1}^{*}, x _{2}^{*}\right)$, जहाँ पर बजट रेखा किसी अनधिमान वक्र पर स्पर्श रेखीय है, उपभोक्ता का इष्टतम बंडल दर्शाती है।

रेखाचित्र 2.12 में उपभोक्ता के इष्टतम को प्रदर्शित किया गया है। $\left(x _{1}^{*}, x _{2}^{*}\right)$ पर बजट रेखा काले रंग वाले अनधिमान वक्र पर स्पर्श रेखीय हैं। ध्यान देने वाली जो पहली बात है वह यह है कि जो अनधिमान वक्र, बजट रेखा को केवल स्पर्श करता है, वह उपभोक्ता के लिए उपलब्ध बजट सेट की दृष्टि से सर्वोच्च अनधिमान वक्र है। इससे ऊपर के अनधिमान वक्रों पर स्थित बंडल, स्लेटी वाले की तरह, उपभोक्ता की सामर्थ्य से बाहर हैं। इससे नीचे के अनधिमान वक्रों पर स्थित बंडल, नीले वाले की तरह उन बिन्दुओं से निश्चित रूप से निम्नस्तरीय होते हैं, जो बजट रेखा को स्पर्श करने वाले अनधिमान वक्रों पर स्थित हैं। बजट रेखा का दूसरा कोई भी बिन्दु निचले अनधिमान वक्र पर स्थित होता है और इस कारण $\left(x _{1}^{*}, x _{2}^{*}\right)$ से निम्नस्तरीय है। इसलिए $\left(x _{1}^{*}, x _{2}^{*}\right)$ उपभोक्ता का इष्टतम बंडल है।

2.4 माँग

पूर्व खंड में हमने उपभोक्ता की चयन समस्या को पढ़ा तथा वस्तुओं की कीमतों, उपभोक्ता की आय और उसके अधिमानों की दी हुई स्थिति में उपभोक्ता के इष्टतम बंडल की व्युत्पत्ति की हमने देखा कि वस्तु की मात्रा जिसका चयन उपभोक्ता इष्टतम रूप में करता है, वस्तु की अपनी कीमत, अन्य वस्तुओं की कीमतों, उपभोक्ता की आय, उसकी रुचि तथा अधिमानों पर निर्भर करता है। किसी वस्तु की मात्रा जो एक उपभोक्ता वस्तुओं की कीमतों, रुचियों एवं अनधिमानों को निश्चित रखते हुए खरीदने को तैयार है और क्षमता रखता है, को वस्तु की मांग कहते हैं। इनमें से एक या एक से अधिक परिवर्तों में परिवर्तन होता है, तो उपभोक्ता द्वारा चयनित वस्तु की मात्रा में भी परिवर्तन आने की संभावना हो जाती है। यहाँ हम इनमें से एक समय एक परिवर्त को बदल कर अध्ययन करते हैं कि कैसे उपभोक्ता द्वारा चयनित वस्तु की मात्रा उस परिवर्त से संबद्ध है।

2.4.1 माँग वक्र तथा माँग का नियम

यदि दूसरी वस्तुओं की कीमत, उपभोक्ता की आय तथा उसकी अभिरुचि और अधिमान अपरिवर्तित रहते हैं, तो किसी वस्तु की मात्रा जिसका उपभोक्ता इष्टतम रूप से चयन करता है, पूरी तरह से उसकी कीमत पर निर्भर हो जाती है। किसी वस्तु की मात्रा के लिए उपभोक्ता का इष्टतम चयन तथा उसकी कीमत में संबंध अत्यंत महत्त्वपूर्ण है तथा यह संबंध माँग फलन कहलाता है। इस प्रकार, किसी वस्तु के लिए उपभोक्ता का माँग फलन वस्तु की वह मात्रा दर्शाता है, जब अन्य वस्तुओं के पूर्ववत् रहने पर उपभोक्ता कीमत के विभिन्न स्तरों पर उसका चयन करता है। उपभोक्ता की माँग इसकी कीमत के एक फलन के रूप में इस प्रकार लिखी जा सकती है:

$$ \begin{equation*} X=f(p) \tag{2.12} \end{equation*} $$

जहाँ $X$ मात्रा को इंगित करता है तथा $p$ वस्तु की कीमत इंगित करता है।

माँग वक्रः किसी उपभोक्ता द्वारा चुनी गई वस्तु की मात्रा और उस वस्तु की कीमत के बीच के संबंध को माँग वक्र कहा जाता है। स्वतंत्र परिवर्त (कीमत) की माप उर्ध्वस्तर अक्ष पर की जाती है तथा परतंत्र परिवर्त की माँग समस्तर अक्ष पर को जाती है। माँग वक्र प्रत्येक कीमत पर उपभोक्ता द्वारा माँग की गई वस्तु की मात्रा को दर्शाता है।

फलन

फलन किन्हीं दो परिवर्तीं $x$ और $y$ के संबंध में विचार करें।

$y=f(x)$

दो परिवर्तों $x$ और $y$ के बीच इस प्रकार संबंध है कि $x$ के प्रत्येक मूल्य के लिए परिवर्त $y$ का एक अद्वितीय मूल्य है। दूसरे शब्दों में, $f(x)$ एक नियम है जो $x$ के प्रत्येक मूल्य के लिए $y$ एक अद्वितीय मूल्य निर्धारित करता है, क्योंकि $y$ का मूल्य $x$ के मूल्य पर निर्भर करता है। अतः $y$ को परतंत्र परिवर्त तथा $x$ को स्वतंत्र परिवर्त कहा जाता है।

उदाहरण 1

एक ऐसी स्थिति के संबंध में विचार करें, जिसमें $x$ के मूल्य $0,1,2,3$ हो सकते हैं और मान लें कि उसके अनुरूप $y$ के मूल्य क्रमशः $10,15,18$ और 20 हैं। यहाँ फलन $y=f(x)$ के द्वारा $y$ और $x$ के बीच संबंध है, जिसे इस तरह परिभाषित किया जाता है: $f(0)=10 ; f(1)=15 ; f(2)=18$ और $f(3)=20$

उदाहरण 2

एक दूसरी स्थिति के संबंध में विचार करें, जिसमें $x$ के मूल्य $0,5,10$ और 20 हो सकते हैं और मान लीजिए कि उसके अनुरूप $y$ के मूल्य क्रमशः $100,90,70$ और 40 है। यहाँ फलन $y=(f x)$ के द्वारा $y$ और $x$ के बीच संबंध है, जिसे इस तरह परिभाषित किया जाता है: $f(0)=100 ; f(10)=90 ; f(15)=70$ और $f(20)=40$

दो परिवर्तों के बीच के फलन संबंध को प्रायः बीजगणितीय रूप में अभिव्यक्त किया जाता है। उदाहरणार्थ:

$$y=5+x \text { और } y=50-x$$

---

यह $x$ के मूल्य के बढ़ने पर $y$ का मूल्य नहीं घटता तो फलन $y=f(x)$ वर्धमान फलन है। यदि $x$ के मूल्य के बढ़ने पर $y$ का मूल्य नहीं बढ़ता, तो यह ह्रासमान प्रतिफल होता है। उदाहरण 1 में दर्शाया गया वर्धमान फलन है। इसी प्रकार फलन $y=x+5$ भी वर्धमान फलन है। उदाहरण 2 में दिया गया फलन ह्रासमान फलन है। फलन $y=50-x$ भी ह्रासमान फलन है।

किसी फलन का ग्राफीय प्रस्तुतीकरण

फलन $y=f(x)$ का ग्राफ उस फलन का ग्राफीय प्रस्तुतीकरण होता है। ऊपर दिए गए उदाहरणों में फलनों के ग्राफ को नीचे दिया गया है।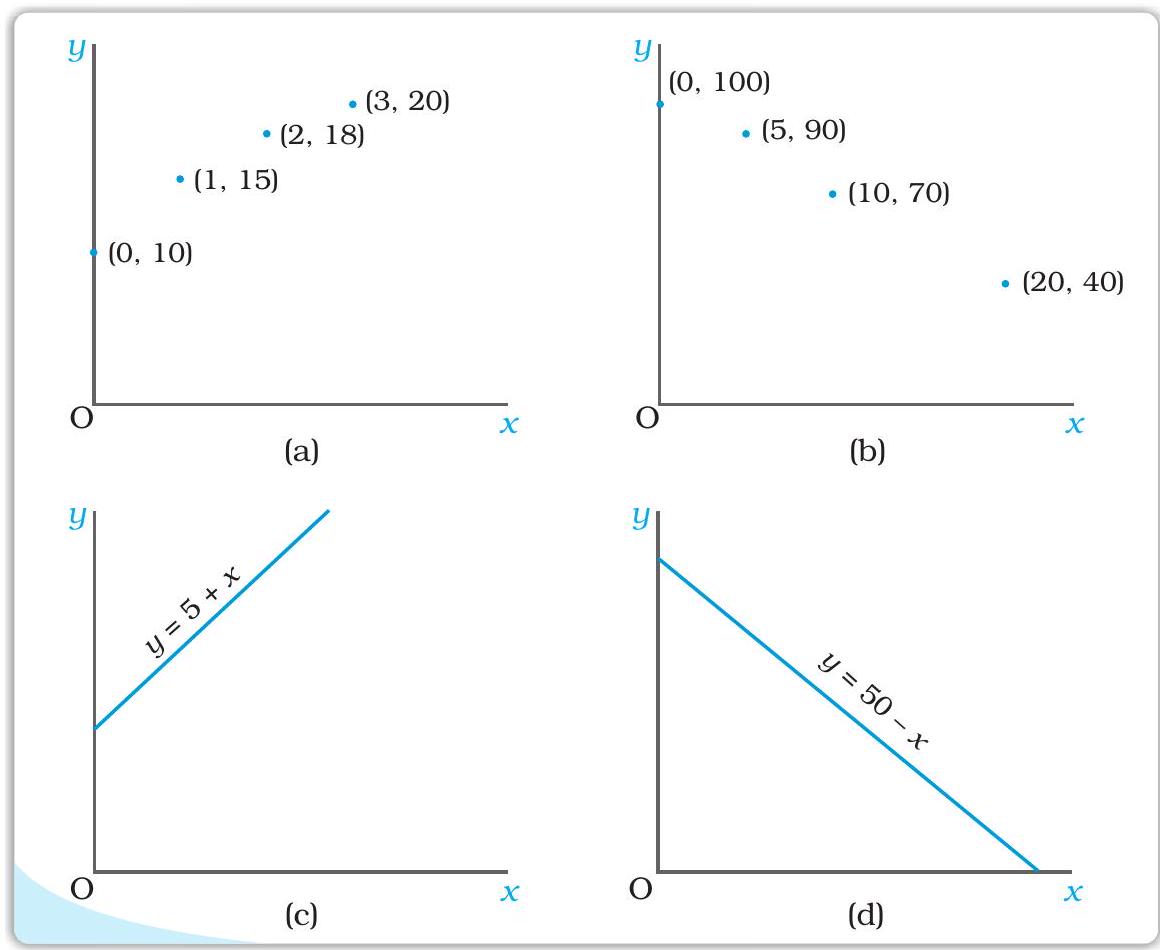

सामान्यतः किसी ग्राफ में स्वतंत्र परिवर्त की माप समस्तर अक्ष पर की जाती है और परतंत्र परिवर्त की माप उर्ध्वस्तर अक्ष पर की जाती है। परन्तु अर्थशास्त्र में कभी-कभी इसके विपरीत भी किया जाता है। उदाहरणार्थ, माँग वक्र को स्वतंत्र परिवर्त (कीमत) को उर्ध्वस्तर अक्ष पर लेकर बनाया जाता है और परतंत्र परिवर्त (मात्रा) को समस्तर अक्ष पर लेकर बनाया जाता है। वर्धमान परिवर्त का ग्राफ ऊपर की ओर बढ़ता हुआ प्रवणता वाला अथवा उर्ध्वस्तरीय होता है और ह्रासमान फलन का ग्राफ नीचे की ओर घटता हुआ प्रवणता वाला अथवा समस्तरीय होता है। जैसा कि हम ऊपर के आरेखों में देख सकते हैं $y=5+x$ का ग्राफ ऊपर की ओर प्रवणता वाला और $y=50-x$ का ग्राफ नीचे की ओर प्रवणता वाला है।

माँग फलन को ग्राफीय रूप में भी दर्शाया जा सकता है जैसे कि रेखाचित्र 2.13 में दर्शाया गया है। माँग फलन का ग्राफीय चित्रण माँग वक्र कहलाता है।

उपभोक्ता का किसी वस्तु के लिए माँग तथा उस वस्तु की कीमत के बीच संबंध साधारणतः नकारात्मक होता है। दूसरे शब्दों में, वस्तु की मात्रा जो उपभोक्ता का इष्टतम चयन होगा, वह वस्तु की कीमत गिरने से संभावित रूप से बढ़ सकता है तथा यह वस्तु की कीमत में वृद्धि होने पर संभावित रूप से घट सकता है।

2.4.2 अनधिमान वक्रों तथा बजट बाध्यताओं से माँग वक्र की व्युत्पत्ति

एक व्यक्ति का विचार कीजिये जो केले $\left(\mathrm{X} _{1}\right)$ तथा आम $\left(\mathrm{X} _{2}\right)$ का उपभोग करता है, जिसकी आम $\mathrm{M}$ हैं, $\mathrm{X} _{1}$ एवं $\mathrm{X} _{2}$ की बाजार कीमतें क्रमशः $\mathrm{P} _{1}^{\prime}$ और $\mathrm{P} _{2}^{\prime}$ हैं। चित्र (a), $\mathrm{C}$ बिन्दू पर उसके उपयोग संतुलन को दिखाता है, जब वह केले और आमों की क्रमशः $\mathrm{X} _{1}^{\prime}$ तथा $\mathrm{X} _{2}^{\prime}$ मात्राएँ खरीदता हैं। चित्र 2.14 के पैनल (b), हम $\mathrm{P} _{1}^{\prime}$ को, $\mathrm{X} _{1}$ के साथ दिखाते हैं जो $\mathrm{X} _{1}^{\prime}$ के माँग वक्र पर प्रथम बिन्दु हैं।

अनधिमान वक्रों तथा बजट बाध्यताओं से माँग वक्र की व्युत्पित्ति

मान लीजिये $\mathrm{X} _{1}$ की कीमत $\overline{\mathrm{P}} _{1}$ तक गिर जाती है और $\mathrm{P} _{2}^{\prime}$ तथा $\mathrm{M}$ स्थिर रहता है। पैनल (a) में बजट सेट विस्तृत हो जाता है और नया उपभोग संतुलन, एक ऊँचे अनधिमान वक्र D पर होता है, जहाँ वह अधिक केले खरीदता है $\left(\overline{\mathrm{X}} _{1}>\mathrm{X} _{1}{ } _{1}\right)$ । इस प्रकार केलों की माँग बढ़ जाती है, और इसकी कीमत गिर जाती है। हम 2.14 के पैनल (b) में, $\overline{\mathrm{P}} _{1}$ को $\overline{\mathrm{X}} _{1}$ के साथ दिखाते हैं, तो हमको माँग वक्र पर दूसरा बिन्दु $\mathrm{X} _{1}$ प्राप्त होता है। इसलिए, केलों की कीमते $\hat{\mathrm{P}} _{1}$ तक और भी कम की जा सकती हैं, जिसके फलस्वरूप केलों के उपभोग में $\hat{\mathrm{X}} _{1}$ तक वृद्धि हो जाती हैं। $\hat{\mathrm{P}} _{1}$ जिसे $\hat{\mathrm{X}} _{1}$ के साथ दिखाया गया है, हमको वक्र पर तृतीय बिन्दु देता है। इस प्रकार, हम देखते हैं कि केलों की कीमतों मे कमी, एक व्यक्ति द्वारा खरीदे गये केलों की मात्रा में वृद्धि करती है, जो अपनी उपयोगिता को अधिकतम कर लेता है। अतः केलों की माँग वक्र ऋणात्मक रूप से ढलवा होता है।

माँग वक्र के ऋणात्मक ढाल के, प्रतिस्थापन एवं आम प्रभाव के आधार पर भी समझाया जा सकता है, जो वस्तुओं की कीमतों में परिवर्तन से क्रियाशील होते हैं।

जब केले सस्ते हो जाते हैं, तो उपभोक्ता अपनी उपयोगिता को केलों के स्थान पर आमों का प्रतिस्थापत कर, अधिकतम कर लेते हैं, ताकि उन्हें कीमत परिवर्तन से वही संतोष प्राप्त हो जाए। फलस्वरूप केलों को मांग मे वृद्धि हो जाती हैं।

इसके अतिरिक्त, जब केलों की कीमत गिरती है, उपभोक्ता की क्रयशक्ति बढ़ जाती है, जो केलों (और आमों) की मांग को और बढ़ा देती है। यह मुख्य परिवर्तत का आय प्रभाव है, जिसके फलस्वरूप केलों की मांग और बढ़ जाती है।

माँग का नियम: यदि किसी वस्तु के लिए किसी उपभोक्ता की माँग उसी दिशा में है जिस दिशा में उपभोक्ता की आय है तो उस वस्तु के लिए उपभोक्ता की माँग का उसकी कीमत के साथ विपरीत संबंध होता है।

रैखिक माँग

रैखिक माँग वक्रः यह चित्र समीकरण 2.13 में दिये गये रैखिक माँग को दर्शाता है।

रैखिक माँग वक्र को साधारणतः इस प्रकार दर्शाया जा सकता है।

$$ \begin{align*} d(p) & =a-b p ; 0 \leq p \leq \frac{a}{b} \\ & =0 ; \quad p>\frac{a}{b} \tag{2.13} \end{align*} $$

जहाँ $a$ उर्ध्वस्तर अंत:खंड है, $-b$ माँग वक्र की प्रवणता है। 0 कीमत पर माँग $a$ है

तथा $\frac{a}{b}$ के बराबर कीमत पर माँग 0 है। माँग वक्र की प्रवणता उस दर की माप करती है, जिस पर कीमत के संदर्भ में माँग में परिवर्तन हो जाती है। वस्तु की कीमत में एक इकाई वृद्धि के लिए माँग $b$ इकाइयाँ गिरती हैं। रेखाचित्र 2.15 में रैखिक माँग वक्र को दर्शाया गया है।

2.4.3 सामान्य और निम्नस्तरीय वस्तुएँ

माँग फलन, उपभोक्ता की वस्तु के लिए माँग तथा इसकी कीमत के बीच का संबंध है, जब अन्य वस्तुएँ दी हुई हों। किसी वस्तु की माँग तथा इसकी कीमत के बीच संबंध के अध्ययन के स्थान पर हम उपभोक्ता की किसी वस्तु के लिए माँग तथा उपभोक्ता की आय के संबंध का भी अध्ययन कर सकते हैं। उपभोक्ता की आय में वृद्धि होने पर किसी वस्तु के लिए उपभोक्ता की माँग बढ़ या घट सकती है और यह वस्तु के स्वरूप पर निर्भर करता है। अधिकतर वस्तु, जिनका चयन उपभोक्ता करता है उसकी मात्रा में वृद्धि होती है, जब उपभोक्ता की आय में वृद्धि होती है तथा वस्तु की मात्रा में कमी आती है जब उपभोक्ता की आय में कमी आती है। ऐसी वस्तुएँ सामान्य वस्तुएँ कहलाती हैं। अतः एक उपभोक्ता की माँग सामान्य वस्तु के लिए उसी दिशा में गति करती है, जिस दिशा में उपभोक्ता की आय। लेकिन, कुछ ऐसी भी वस्तुएँ हैं जिनके लिए माँग उपभोक्ता की आय के विपरीत दिशा में जाती है। ऐसी वस्तुओं को निम्नस्तरीय वस्तुएँ कहा जाता है। उपभोक्ता की आय जैसे-जैसे बढ़ती है, निम्नस्तरीय वस्तुओं के लिए माँग घटती जाती है और आय जैसे-जैसे घटती है निम्नस्तरीय वस्तुओं की माँग बढ़ जाती है। निम्नस्तरीय वस्तुओं के उदाहरण हैं, जैसे-निम्नस्तरीय खाद्य पदार्थ, मोटे अनाज।

उपभोक्ता की क्रय शक्ति (आय) में वृद्धि कभी-कभी उपभोक्ता को वस्तुओं के उपभोग में कमी लाने को प्रेरित कर सकती है। ऐसी स्थिति में प्रतिस्थापन्न प्रभाव तथा आय प्रभाव एक दूसरे के विपरीत दिशा में कार्य करते हैं। ऐसे वस्तुओं की माँग सकारात्मक अथवा नकारात्मक रूप से कीमतों से संबद्ध हो सकती है, जो कि इन दो विपरीत प्रभावों वाले शक्तियों से संबंधित है। यदि प्रतिस्थापन्न प्रभाव, आय प्रभाव से अधिक है, तो इस दशा में वस्तु की माँग तथा वस्तु की कीमत विपरीत रूप से संबद्ध होंगे। यद्यपि, यदि आय प्रभाव ज़्यादा प्रभावकारी है, प्रतिस्थापन्न प्रभाव से तो वस्तु की माँग उसकी कीमत से सकारात्मक रूप से संबद्ध होगी। इस तरह की वस्तु को ‘गिफिन वस्तु’ कहा जाता है।

कुछ वस्तुएँ किसी उपभोक्ता के लिए आय के कुछ स्तरों पर सामान्य वस्तु हो सकती है तथा अन्य स्तरों पर निम्नस्तरीय वस्तु हो सकती है। उपभोक्ता की आय यदि अत्यंत नीचे के स्तर पर है, तो उसकी आय के बढ़ने पर निम्न कोटि के खाद्यान्नों के लिए उसकी माँग बढ़ जाएगी। लेकिन एक स्तर के बाद उपभोक्ता की आय, यदि बढ़ जाती है तो ऐसे खाद्यान्रों के लिए उसकी माँग घट सकती है, जैसे ही वह बेहतर गुणवत्ता वाले खाद्य पदार्थों को खरीदना प्रारंभ कर देता है।

2.4.4 स्थानापन्न तथा पूरक

हम उपभोक्ता द्वारा चुनी जाने वाली वस्तु की मात्रा तथा किसी संबद्ध वस्तु की कीमत के बीच संबंध का भी अध्ययन कर सकते हैं। एक वस्तु की मात्रा जिसका चयन उपभोक्ता करता है, किसी संबद्ध वस्तु को मूल्य में वृद्धि के साथ बढ़ सकती है अथवा घट सकती है। ऐसा होना इस पर निर्भर करता है कि दोनों वस्तुएँ स्थानापन्न हैं अथवा एक-दूसरे के पूरक हैं। जिन वस्तुओं का साथ-साथ उपयोग किया जाता है, उन्हें पूरक वस्तुएँ कहा जाता है। इनके उदाहरण हैं, चाय तथा चीनी, जूते तथा जुराब, कलम तथा स्याही आदि। क्योंकि चाय तथा चीनी एक साथ उपयोग में लाए जाते हैं, संभव है कि चीनी की कीमत में वृद्धि चाय के लिए माँग घटाएगी तथा चीनी की कीमत में गिरावट संभवतः चाय की माँग को बढ़ाएगी। अन्य पूरकों के साथ भी ऐसा ही होता है। समान्यत: किसी वस्तु के लिए माँग की गति उसको पूरक वस्तुओं की कीमत के विपरीत दिशा में होती है।

पूरकों के विपरीत चाय व कॉफी जैसी वस्तुओं का एक साथ उपभोग नहीं होता। वास्तव में वे एक-दूसरे के लिए स्थानापन्न होती है। क्योंकि चाय कॉफी का स्थानापन्न है, अतः यदि कॉफी की कीमत में वृद्धि होती है, तो उपभोक्ता चाय की ओर जा सकते हैं और इस प्रकार चाय का उपभोग संभवतः अधिक हो सकता है। दूसरी ओर, यदि कॉफी को कीमत घटती है, तो चाय का उपभोग संभवतः नीचे जा सकता है। साधातणतः किसी वस्तु की माँग उसके स्थानापन्न वस्तु की कीमत की दिशा में गति करती है।

2.4.5 माँग वक्र में शिफ्ट

माँग वक्र यह मानकर बनाया गया था कि उपभोक्ता की आय, अन्य वस्तुओं की कीमतें तथा उपभोक्ता का अधिमान दिया गया है। यदि इनमें से कोई वस्तु बदलती है, तो माँग वक्र में किस प्रकार का परिवर्तन होता है?

(a)

(b)

रेखाचित्र 2.16

माँग में शिफ्ट: पैनल (a) में माँग वक्र का शिफ्ट बाईं ओर होता है और पैनल (b) में शिफ्ट दाईं ओर होता है।

अन्य वस्तुओं की कीमतों और किसी उपभोक्ता के अधिमान दिए हुए होने पर, यदि उसकी आय में वृद्धि होती है, तो प्रत्येक कीमत पर वस्तु के लिए माँग में परिवर्तन होता है और इस प्रकार माँग वक्र शिफ्ट हो जाता है। सामान्य वस्तुओं के लिए माँग वक्र का शिफ्ट दाईं ओर तथा निम्नस्तरीय वस्तुओं के लिए माँग वक्र का शिफ्ट बाईं ओर होता है।

उपभोक्ता की आय और उसके अधिमान के दिए होने की स्थिति में, यदि संबंधित वस्तु की कीमत में परिवर्तन होता है तब किसी वस्तु की कीमत के प्रत्येक स्तर पर उस वस्तु के लिए माँग में परिवर्तन हो जाता है और इस प्रकार माँग वक्र शिफ्ट हो जाता है। यदि स्थानापन्न वस्तु की कीमत बढ़ती है, तब माँग वक्र दाईं ओर शिफ्ट होता है। इसके विपरीत यदि पूरक वस्तु की कीमत बढ़ती है, तो माँग वक्र का शिफ्ट बाईं ओर होता है।

उपभोक्ता की रुचियों और अधिमानों में परिवर्तन के कारण भी माँग वक्र का शिफ्ट हो सकता है। उपभोक्ता का अधिमान में परिवर्तन यदि किसी वस्तु के पक्ष में होता है, तब ऐसी वस्तु के लिए माँग वक्र का शिफ्ट दाईं ओर होगा। इसके विपरीत उपभोक्ता के अधिमान में परिवर्तन यदि प्रतिकूल होता है, तब माँग वक्र का शिफ्ट बाईं ओर होता है। उदाहरणार्थ, गर्मी के मौसम में आइसक्रीम के माँग वक्र का दाईं ओर शिफ्ट होगा, क्योंकि इस मौसम में आइसक्रीम को लोग अधिक पसंद करते हैं। इस तथ्य का लोगों के सामने आना कि शीतल पेय स्वास्थ्य के लिए हानिकारक हो सकते हैं, शीतपेयों के प्रति अधिमानों को बुरे तरीके से प्रभावित करेगा। इसके फलस्वरूप शीतल पेय के लिए माँग वक्र का बाईं ओर शिफ्ट होने की संभावना होती है।

रेखाचित्र 2.16 माँग वक्र में शिफ्ट को दर्शाया गया है। यह बताना जरूरी है, कि मांग वक्र में शिफ्ट तब होता है, जब कीमत के अलावा किसी अन्य कारक में परिवर्तन होता है।

2.4.6 माँग वक्र की दिशा में गति और माँग वक्र में शिफ्ट

जैसा कि हमने पहले देखा है कि कोई उपभोक्ता किसी वस्तु की कितनी मात्रा का चयन करता है, यह वस्तु की कीमत, अन्य वस्तुओं की कीमतें, उपभोक्ता की आय तथा उसकी रुचियों और अधिमानों पर निर्भर करता है। माँग फलन वस्तु की मात्रा और उसकी कीमत के बीच का उस समय का संबंध होता है, जब अन्य वस्तुएँ अपरिवर्तित रहती है। माँग वक्र माँग फलन का ग्राफीय चित्रण होता है। ऊँची कीमतों पर माँग कम होती है और कम कीमतों पर माँग अधिक होती है। अतः कीमत में कोई भी परिवर्तन होने के फलस्वरूप माँग वक्र की दिशा में गति होती है। इसके विपरीत, किन्हीं अन्य वस्तुओं में परिवर्तनों के फलस्वरूप माँग वक्र शिफ्ट हो जाता है। रेखाचित्र 2.17 में माँग वक्र की दिशा में गति और माँग वक्र के शिफ्ट को दर्शाया गया है।

माँग वक्र की दिशा में गति और माँग वक्र का शिफ्ट: पैनल (a) माँग वक्र की दिशा में गति को चित्रित करता है और पैनल (b) माँग वक्र के शिफ्ट को चित्रित करता है।

2.5 बाज़ार माँग

पूर्व खण्ड में हमने किसी उपभोक्ता की चयन की समस्या का अध्ययन किया और उपभोक्ता का माँग वक्र प्राप्त किया। परन्तु बाज़ार में एक ही वस्तु के लिए अनेक उपभोक्ता होते हैं। किसी वस्तु के लिए बाज़ार माँग को जानना महत्त्वपूर्ण होता है। किसी वस्तु के लिए एक विशेष कीमत पर बाज़ार माँग सभी उपभोक्ताओं की सम्मिलित माँग का जोड़ होती है। किसी भी वस्तु के लिए बाज़ार माँग व्यक्ति विशेष के माँग वक्रों से प्राप्त की जा सकती है। मान लीजिए, एक वस्तु के लिए बाज़ार में केवल दो ही उपभोक्ता है: मान लीजिए, कीमत $p^{\prime}$ पर, उपभोक्ता 1 की माँग

बाज़ार माँग वक्र की व्युत्पत्ति: बाज़ार माँग वक्र विशिष्ट माँग वक्रों के समस्तरीय संकलन से प्राप्त किया जा सकता है।

$q _{1}^{\prime}$ है तथा उपभोक्ता 2 की माँग $q _{2}^{\prime}$ है। तब कीमत $p^{\prime}$ पर वस्तु की बाज़ार माँग $q _{1}^{\prime}+q _{2}^{\prime}$ है। उसी प्रकार कीमत $\hat{p}$ पर यदि उपभोक्ता 1 की माँग $\hat{q} _{1}$ है तथा उपभोक्ता 2 की माँग $\hat{q} _{2}$ है तब कीमत $\hat{p}$ पर वस्तु की बाज़ार माँग $\hat{q} _{1}+\hat{q} _{2}$ है। अतः किसी वस्तु के लिए प्रत्येक कीमत पर दो उपभोक्ताओं की माँगों को उस मूल्य पर जोड़ कर बाज़ार माँग निकाली जा सकती है। यदि किसी वस्तु के लिए बाज़ार में दो से अधिक उपभोक्ता हैं, तो बाज़ार माँग उसी प्रकार प्राप्त की जा सकती है।

जैसा कि रेखाचित्र 2.18 में दर्शाया गया है, अलग-अलग व्यक्तियों के समस्तरीय माँग वक्रों का ग्राफीय रूप में चित्रण करके भी बाज़ार माँग वक्र प्राप्त किया जा सकता है। इसके लिए अलग-अलग व्यक्तियों के समस्तरीय माँग वक्रों को जोड़ना होगा। दो वक्रों को जोड़ने की इस विधि को समस्तरीय संकलन कहा जाता है।

दो रैखिक माँग वक्रों का जोड़

उदाहरण के लिए एक ऐसा बाज़ार लेते हैं जहाँ दो उपभोक्ता हैं और इन दोनों के माँग समीकरण नीचे दिए गए हैं।

$$ \begin{align*} d _{1}(p)=10-p \tag{2.14} \\ \text { तथा } \quad d _{2}(p)=15-p \tag{2.15} \end{align*} $$

इसके अतिरिक्त 10 से अधिक किसी भी कीमत पर उपभोक्ता वस्तु 1 की 0 इकाइयों की माँग करता है तथा उसी प्रकार 15 से अधिक किसी भी कीमत पर उपभोक्ता वस्तु 2 की 0 इकाइयों की माँग करता है तथा बाज़ार माँग समीकरणों (2.14) तथा (2.15) को जोड़कर निकाली जा सकती है।

किसी भी कीमत पर जो 10 के बराबर हो अथवा उससे कम हो बाज़ार माँग $25-2 p$ द्वारा दी जाएगी तथा किसी भी कीमत पर जो 15 इकाइयों से अधिक हो, बाज़ार माँग 0 होगी तथा किसी भी कीमत पर जो 10 से अधिक है और 15 से कम है या उसके बराबर है, बाज़ार माँग $15-p$ होगी।

2.6 माँग की लोच

किसी भी वस्तु के लिए माँग उसकी कीमत के विपरीत दिशा में जाती है। परन्तु कीमत में परिवर्तन का प्रभाव सदैव समान नहीं रहता। कभी-कभी छोटे से कीमत परिवर्तनों के कारण भी माँग में अत्यधिक परिवर्तन हो जाती है। इसके विपरीत, कुछ वस्तुएँ ऐसी भी हैं जिनके लिए माँग, कीमत परिवर्तनों के कारण अधिक प्रभावित नहीं होती। कुछ वस्तुओं के लिए माँग कीमत परिवर्तनों के प्रति अत्यधिक अनुक्रियात्मक होती है जबकि अन्य वस्तुओं के लिए कीमत परिवर्तनों के कारण माँग इतनी अधिक अनुक्रियात्मक नहीं होती। माँग की कीमत-लोच वस्तु के कीमत परिवर्तन के कारण इसकी माँग की अनुक्रियात्मकता की माप है। माँग की कीमत लोच की परिभाषा इस प्रकार दी जा सकती है: किसी वस्तु की माँग में प्रतिशत परिवर्तन को उस वस्तु की कीमत में प्रतिशत परिवर्तन से भाग देने पर प्राप्त भागफल किसी वस्तु के लिए माँग की कीमत लोच है। एक वस्तु के लिए माँग की कीमत लोच,

$$\begin{align*} e _{D} & =\frac{\text { वस्तु के लिए माँग में प्रतिशत परिवर्तन }}{\text { वस्तु की कीमत में प्रतिशत परिवर्तन }} \tag{2.16a}\\ & =\frac{\frac{\Delta Q}{Q} \times 100}{\frac{\Delta P}{P} \times 100} \tag{2.16b}\\ & =\left(\frac{\Delta Q}{Q}\right) \times\left(\frac{P}{\Delta P}\right) \end{align*}$$

जहाँ $\Delta P$ वस्तु की कीमतों में परिवर्तन है और $\Delta Q$ वस्तु की मात्रा में परिवर्तन है।

उदाहरण 2.2

मान लीजिये रु 5 प्रति केले के भाव पर, एक उपभोक्ता 15 केले खरीदता हैं। जब कीमत रु 7 प्रति केले हो जाती है, तो उसकी मांग घटकर 12 केले रह जाती हैं।

उसकी केलों के लिये माँग की लोच ज्ञात करने लिये, हम माँगी जाने वाली मात्रा और इसकी

कीमत में प्रतिशत परिवर्तन को तालिका में दी गई संरचना का उपयोग करते हुए निकालते हैं।

ध्यान दीजिये, माँग की कीमत लोच एक ऋणात्मक संख्या होती हैं, क्योंकि वस्तु की माँग, वस्तु के मूल्य से ऋणात्मक रूप से संबंधित होती है। फिर भी, सरलता के लिए हम लोच के निरपेक्ष मान को ही लेते हैं।

मांगी जाने वाली मात्रा में प्रतिशत परिवर्तन $=\frac{\Delta Q}{\Theta_{1}} \times 100$

$$ \begin{aligned} & =\left(\frac{\mathcal{Q} _{2}-\mathcal{Q} _{1}}{\mathcal{G} _{1}}\right) \times 100 \\ & =\frac{12-15}{15} \times 100=-20 \end{aligned} $$

बाज़ार कीमत में प्रतिशत परिवर्तन $=\frac{\Delta P}{P_{1}} \times 100$

$$ \begin{aligned} & =\left(\frac{P _{2}-P _{1}}{P _{1}}\right) \times 100 \\ & =\frac{7-5}{5} \times 100=40 \end{aligned} $$

इसलिये उदाहरण में, जब केलों की कीमतें 40 प्रतिशत बढ़ती है, तो केलों की माँग 20 प्रतिशत घट जाती है। मांग की कीमत लोच $\left|e_{D}\right|=\frac{20}{40}=0.5$ है। स्पष्टतः, केलों की मांग, केलों की कीमतों की अपेक्षा अधिक खर्चीली नहीं है। जब मांगे जाने वाली मात्रा में प्रतिशत परिवर्तन, कीमतों में प्रतिशत परिवर्तनों से कम होते हैं, तो $\left|e_{D}\right|$ को 1 से कम अनुमानित किया जाता है और उस कीमत पर वस्तु की मांग बेलोचदार कही जाती हैं। अनिवार्य वस्तुओं की माँग बहुधा बेलोचदार पाई जाती है।

जब माँगे जाने वाली मात्रा में प्रतिशत परिवर्तन, बाज़ार मूल्य में प्रतिशत परिवर्ततों से अधिक होते हैं, तो माँग बाज़ार मूल्य में परिवर्तनों के काफी अनुक्रियात्मक होती है और $\left|e_{D}\right|$ को 1 से अधिक अनुमानित किया जाता हैं। दी गई कीमत पर, वस्तु की माँग लोचदार होती है। विलासिता की वस्तुओं की मांग, बाज़ार मूल्यों के परिवर्तनों के काफी अनुक्रियाशील होते हैं और उसकी माँग की लोच 1 से अधिक $\left(\left|e_{D}\right|>1\right)$ होती है।

जब मांगे जाने वाली मात्रा में प्रतिशत परिवर्तन, बाजार मूल्य में प्रतिशत परिवर्तन के बराबर होते हैं, तो को 1 के बराबर अनुमानित किया जाता है और वस्तु के लिये मांग की लोच इकाई के बराबर होती हैं। ध्यान रखिये कि कुछ वस्तुओं के लिये मांग की लोच, लोचदार, इकाई के बराबर लोचदार अथवा बेलोचदार हो सकती हैं। वास्तव में (अगले परिच्छेद में) एक रेखीय मांग वक्र के साथ, मांग की लोच विभिन्न कीमतों पर अनुमानित की जाती हैं और नीचे की ओर ढलवा मांग वक्र के प्रत्येक बिन्दु पर अलग अलग दिखाई जाती है।

2.6.1 रैखिक माँग वक्र की दिशा में लोच

आइए, एक रैखिक माँग वक्र $q=a-b p$ का विश्लेषण करें। ध्यान दीजिए कि माँग वक्र की किसी भी बिन्दु पर माँग में परिवर्तन प्रति इकाई कीमत परिवर्तन है $\frac{\Delta q}{\Delta p}=-b$ (2.16b) में $\frac{\Delta q}{\Delta p}$ के मान को स्थानापन्न करने पर हमें प्राप्त होता है $=-b \frac{p}{q}$

$q$ का मूल्य रखने पर,

$$ \begin{equation*} e_{D}=-\frac{b p}{a-b p} \tag{2.17} \end{equation*} $$

**2.**17 से यह स्पष्ट है कि एक रैखिक माँग वक्र के विभिन्न बिन्दुओं पर माँग की लोच भिन्न होती है। $p=0$ पर लोच 0 है तथा $q=0$ पर लोच $\infty$ है। $p=\frac{a}{2 b}$ पर लोच 1 है; किसी भी कीमत पर जो 0 से अधिक हो परन्तु $\frac{a}{2 b}$ की

रेखाचित्र 2.19

माँग वक्र की दिशा में लोच: 1 माँग की कीमत लोच रैखिक माँग वक्र पर अलग-अलग बिन्दुओं पर भिन्न है। तुलना में कम हो, लोच 1 से कम है तथा किसी भी मूल्य पर लोच 1 से अधिक है जब कीमत $\frac{a}{2 b}$ की तुलना में अधिक है। रेखाचित्र 2.19 में एक रैखिक वक्र पर माँग की कीमत लोच को, जिसे समीकरण में दर्शाया गया है।

रैखिक माँग वक्र की दिशा में लोच की ज्यामितीय माप

एक रैखिक माँग वक्र की लोच आसानी से ज्यामितीय पद्धति से मापी जा सकती है। एक सीधी रेखा रूपी माँग वक्र के किसी भी बिन्दु पर माँग की लोच माँग वक्र के नीचे वाले खंड में तथा ऊपर वाले खंड के बीच उस बिन्दु पर अनुपात के रूप में दी जाती है। ऐसा क्यों है, यह देखने के लिए नीचे दिए गए रेखाचित्र पर गौर कीजिए जो दर्शाती है एक सीधी रेखा रूपी माँग वक्र $q=a-b p$.

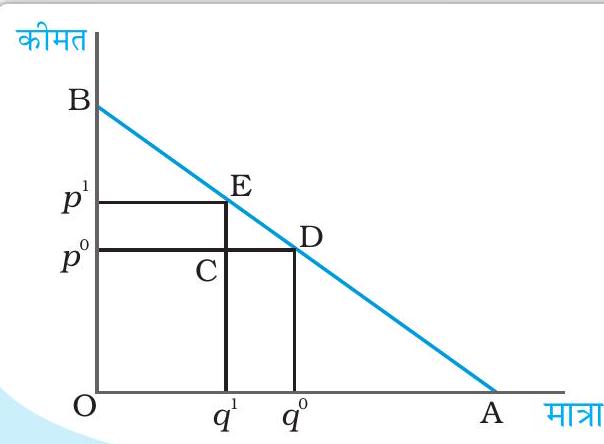
मान लीजिए, कीमत $p^{0}$ पर वस्तु के लिए माँग $q^{0}$ है। अब एक छोटे से कीमत परिवर्तन पर गौर कीजिए। नई कीमत $p^{1}$ है तथा उस कीमत पर वस्तु के लिए $q^{1}$ माँग है। $\Delta q=q^{1} q^{0}=C D$ तथा $\Delta p=p^{1} p^{0}=C E$.

अत: $e_{D}=\frac{\Delta q / q^{0}}{\Delta p / p^{0}}=\frac{\Delta q}{\Delta p} \times \frac{p^{0}}{q^{0}}=\frac{q^{1} q^{0}}{p^{1} p^{0}} \times \frac{O p^{0}}{O q^{0}}=\frac{C D}{C E} \times \frac{O p^{0}}{O q^{0}}$

क्योंकि $E C D$ तथा $B p^{0} D$ समान त्रिकोण हैं, $\frac{C D}{C E}=\frac{p^{0} D}{p^{0} B}$ परन्तु $\frac{p^{0} D}{p^{0} B}=\frac{O q^{0}}{p^{0} B}$

$e_{D}=\frac{O p^{0}}{P^{0} B}=\frac{q^{0} D}{P^{0} B}$

क्योंकि $B p^{0} d$ तथा $B O A$ समान त्रिकोण हैं $\frac{q^{0} D}{p^{0} B}=\frac{D A}{D B}$.

अत: $e_{D}=\frac{D A}{D B}$

माँग की लोच एक सीधी रेखा रूपी माँग वक्र के विभिन्न बिन्दुओं पर, इस ज्यामितीय तरीके से प्राप्त की जा सकती है। उस बिन्दु पर लोच 0 है जहाँ माँग वक्र समस्तरीय अक्ष से मिलता है तथा यह उस बिन्दु पर $\infty$ है जहाँ माँग वक्र ऊर्ध्वस्तर अक्ष से मिलता है। माँग वक्र के मध्य बिन्दु पर लोच 1 है, तथा बायों ओर किसी भी बिन्दु पर यह 1 से अधिक है तथा दायीं ओर किसी भी बिन्दु पर यह 1 से कम है। ध्यान दीजिए कि समस्तरीय अक्ष पर $p=0$, उर्ध्वस्तर अक्ष पर $q=0$ तथा माँग वक्र के मध्य बिन्दु पर $p=\frac{a}{2 b}$

स्थिर लोच माँग वक्र

रैखिक माँग वक्र पर विभिन्न बिन्दुओं पर, माँग की लोच 0 से $\infty$ तक परिवर्तित हुए भिन्न है। परन्तु कभी-कभी माँग वक्र ऐसा हो सकता है कि माँग की लोच पूरी तरह से स्थिर रहे। उदाहरण के लिए, एक

स्थिर लोच माँग वक्र: जैसा कि पैनल (a) में दर्शाया गया है उर्ध्वस्तरीय माँग वक्र को दिशा में सभी बिन्दुओं पर माँग की लोच 0 है। पैनल (b) में क्षैतिजीय माँग वक्र के समस्त बिन्दुओं पर माँग की लोच $\infty$ है। पैनल (c) में माँग वक्र के सभी बिन्दुओं पर लोच 1 है।

उर्ध्वस्तर माँग वक्र लीजिए जैसा कि रेखाचित्र 2.20 (a) में दर्शाया गया है। जो भी कीमत हो, स्तर $\bar{q}$ पर माँग दी गई है। ऐसे माँग वक्र के लिए कीमत में परिवर्तन भी कभी माँग में परिवर्तन का कारण नहीं बनता तथा सदा ही $\left|e_{D}\right|=0$ अतः एक ऊर्ध्वस्तर माँग वक्र पूर्ण रूप से लोचहीन होता है।

रेखाचित्र 2.20 (b) एक क्षैतिजीय मांग वक्र को दिखाता है जहाँ बाजार मूल्य $\overline{\mathrm{P}}$ पर स्थिर रहता है, चाहे वस्तु के लिये मांग की स्तर कुछ भी हो। किसी अन्य बिन्दु पर, मांगी जाने वाली मात्रा शून्य हो जाती है, इसलिये $\left|e_{D}\right|=\infty$, एक क्षैतिजीय मांग वक्र पूर्णतया लोचदार होता हैं।

रेखाचित्र 2.20 (c) एक माँग वक्र दर्शाता है, जिसकी आकृति एक समकोणीय अतिपरवलय की है। इस माँग वक्र में यह गुण है कि माँग वक्र की दिशा में कीमत में प्रतिशत परिवर्तन, मात्रा में सदा समान प्रतिशत परिवर्तन लाता है। अतः इस माँग वक्र के प्रत्येक बिन्दु पर $\left|e_{D}\right|=1$ इस माँग वक्र को इकाई लोचदार माँग कहा जाता है।

2.6.2 किसी वस्तु के लिए माँग की कीमत लोच को निर्धारित करने वाले कारक

किसी वस्तु के लिए माँग की कीमत लोच वस्तु की प्रकृति और वस्तु के निकटतम स्थानापन्न वस्तु की उपलब्धता पर निर्भर करती है। उदाहरण के लिए, खाद्य पदार्थों जैसे आवश्यक वस्तुओं के संबंध में विचार करें। ऐसी वस्तुएँ जीवन के लिए आवश्यक होती हैं तथा उनकी कीमतों में परिवर्तन होने पर उनके लिए माँग में बहुत परिवर्तन नहीं होता। खाद्यान्नों की कीमतों के बढ़ने पर भी उनके लिए माँग में बहुत परिवर्तन नहीं होता। इसके विपरीत, विलासिता की वस्तुओं की माँग पर उनकी कीमत में परिवर्तन का अत्यधिक प्रभाव पड़ता है। सामान्यतः आवश्यक वस्तुओं के लिए माँग की कीमत लोचहीन होने की संभावना होती है जब कि विलासिता की वस्तुओं के लिए माँग की कीमत लोचदार होने की संभावना होती है।

यद्यपि खाद्य पदार्थों के लिए माँग लोचहीन होती है परन्तु कुछ विशेष प्रकार के खाद्य पदार्थों के लिए माँग लोचदार हो सकती है। जैसे कि कुछ विशेष किस्म की दालों को ही ले लीजिए। यदि किसी विशेष किस्म की दाल की कीमत बढ़ जाती है, तो लोग किसी अन्य दाल का उपभोग करने लगेंगे, जो उसका निकट का स्थानापन्न है। उस वस्तु की माँग लोचदार होती है, जिसकी निकट की स्थानापन्न वस्तुएँ सरलतापूर्वक उपलब्ध है। इसके विपरीत, यदि निकट की स्थानापन्न वस्तुएँ सरलतापूर्वक उपलब्ध नहीं हैं, तो ऐसी वस्तु के लिए माँग लोचहीन होगी।

2.6.3 लोच तथा व्यय

किसी वस्तु पर व्यय उस वस्तु की माँग के बराबर होता है, जो उस वस्तु की कीमत का गुणक है। प्राय: यह जानना महत्त्वपूर्ण होता है कि किसी वस्तु की कीमत में बदलाव से उस पर होने वाले खर्च में कैसे परिवर्तन आता है। वस्तु की कीमत तथा उस वस्तु के लिए माँग एक-दूसरे से प्रतिलोमतः संबद्ध हैं। कीमतों में परिवर्तन के फलस्वरूप उस वस्तु पर किए जाने वाले व्यय में वृद्धि होती है अथवा कमी, यह इस बात पर निर्भर करता है कि कीमत में परिवर्तन के प्रति उस वस्तु की माँग कितनी अनुक्रियात्मक है।

किसी एक वस्तु की कीमत में वृद्धि को लीजिए। यदि मात्रा में प्रतिशत गिरावट कीमत में प्रतिशत वृद्धि की तुलना में अधिक है, तो वस्तु पर होने वाला व्यय कम हो जाएगा। उदाहरण के लिए, तालिका 2.5 में पंक्ति 2 को देखें, जो दिखाती है कि जैसे ही वस्तु की कीमत $10 %$ बढ़ती है, इसकी माँग $12 %$ गिर जाती है, जिसके फलस्वरूप वस्तु पर होने वाला कुल व्यय गिर जाता है। दूसरी ओर, यदि मात्रा में प्रतिशत गिरावट कीमत में प्रतिशत वृद्धि की तुलना में कम हो, तो वस्तु पर व्यय अधिक होगा (तालिका 2.5 में पंक्ति 1 को देखें) और यदि प्रतिशत मात्रा में कमी कीमत में प्रतिशत वृद्धि के बराबर हो, तो वस्तु पर व्यय अपरिवर्तित रहेगा (तालिका 2.5 में पंक्ति 3 को देखें)।

अब वस्तु की कीमत में गिरावट पर विचार करें। यदि मात्रा में प्रतिशत वृद्धि कीमत में प्रतिशत गिरावट की तुलना में अधिक है, तो वस्तु पर व्यय में वृद्धि हो जाएगी (तालिका 2.5 में पंक्ति 4 को देखें)। इसके विपरीत, यदि मात्रा में प्रतिशत वृद्धि कीमत में प्रतिशत गिरावट की तुलना में कम है, तो वस्तु पर किये गये व्यय में गिरावट आ जाएगी (तालिका 2.5 में पंक्ति 5 को देखें)। और यदि मात्रा में प्रतिशत वृद्धि कीमत में प्रतिशत गिरावट के समान है, तो वस्तु पर व्यय अपरिवर्तित रहेगा (तालिका 2.5 में पंक्ति 6 को देखें)।

कीमत में परिवर्तन होने पर वस्तु पर व्यय में परिवर्तन तभी विपरीत दिशा में जाएगा, जब मात्रा में प्रतिशत परिवर्तन कीमत में प्रतिशत परिवर्तन से अधिक है अर्थात्, यदि वस्तु की कीमत लोचदार है (तालिका 2.5 में पंक्ति 2 और 4 को देखें)। वस्तु पर व्यय में परिवर्तन तथा कीमत में परिवर्तन तभी समान दिशा में होगा जब केवल मात्रा में प्रतिशत परिवर्तन कीमत में प्रतिशत परिवर्तन की तुलना में कम हो अर्थात्, यदि वस्तु की कीमत लोचहीन है (तालिका 2.5 में पंक्ति 1 और 5 को देखें)। वस्तु पर व्यय तभी अपरिवर्तित रहेगा यदि केवल मात्रा में प्रतिशत परिवर्तन कीमत में प्रतिशत परिवर्तन के समान है, अर्थात् यदि वस्तु इकाई लोच वाली है (तालिका 2.5 में पंक्ति 3 और 6 को देखें)।

तालिका 2.5: कीमत वृद्धि एवं ह्रास के कुछ काल्पनिक उदाहरणों से, निम्न तालिका किसी वस्तु पर व्यय तथा लोच के बीच संबंध को स्पष्ट करती है।

आयताकार अतिपरवलय

इसका समीकरण है

$x y=c $

जहाँ $x$ तथा $y$ तो चर है तथा $c$ स्थिर है, हमें एक वक्र प्रदान करता है, जिसे आयताकार अतिपरवलय कहा जाता है। यह नीचे की ओर प्रवणता वाला $x-y$ समतल पर स्थित एक वक्र है, जिसे रेखाचित्र में दर्शाया गया है। वक्र पर किसी भी दो बिन्दुओं $p$ तथा $q$ दो आयताकारों $\mathrm{O} y_{1} p x_{1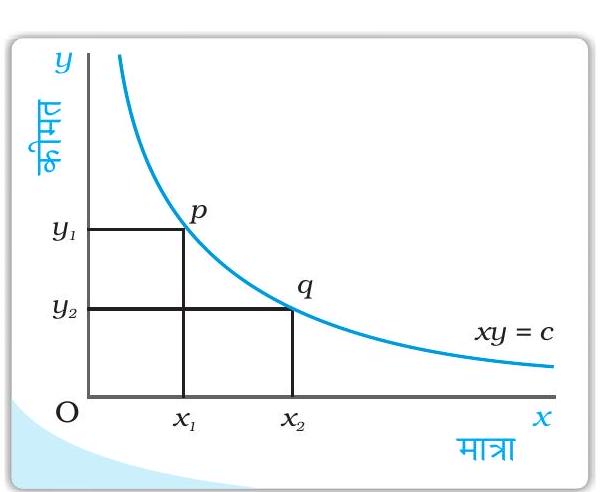}$ तथा $\mathrm{O} y_{2} q x_{2}$ समान है तथा $c$ के बराबर हैं।

यदि माँग वक्र का समीकरण $p q=e$ का स्वरूप ग्रहण करता है, जहाँ $e$ स्थिर है, तब वह एक आयताकार अतिपरवलय होगा। यहाँ कीमत गुणा मात्रा स्थिर है, ऐसे माँग वक्र में यह कोई मायने नहीं रखता कि उपभोक्ता किस बिंदु का उपभोग करता है। उसका खर्च हमेशा समान तथा $e$ के बराबर होगा।

किसी वस्तु पर व्यय और लोच में परिवर्तन के बीच संबंध

मान लीजिए, कीमत $p$ पर किसी वस्तु के लिए माँग $q$ है तथा कीमत $p+\Delta p$ पर वस्तु के लिए माँग $q+\Delta q$ है।

कीमत $p$ पर वस्तु पर सम्पूर्ण व्यय $p q$ है तथा कीमत $p+\Delta p$ पर वस्तु पर सम्पूर्ण व्यय $(p+\Delta p)(q+\Delta q)$ है।

यदि कीमत में परिवर्तन $p$ से $(p+\Delta p)$ होता है, तो वस्तु पर व्यय में परिवर्तन है $(p+$ $\Delta p)(q+\Delta q)-p q$

$=q \Delta p+p \Delta q+\Delta p \Delta q$

$\Delta p$ तथा $\Delta q$ के छोटे मानों के लिए $\Delta p \Delta q$ पद का मूल्य नगण्य है तथा उस स्थिति में वस्तु पर व्यय में सन्निकट परिवर्तन $q \Delta p+p \Delta q$ द्वारा दिया जा सकता है।

व्यय में सन्निकट परिवर्तन $=\Delta E=q \Delta p+p \Delta q=\Delta p\left(q+p \frac{\Delta q}{\Delta p}\right)$

$=\Delta p\left[q\left(1+\frac{\Delta q}{\Delta p} \frac{p}{q}\right)\right]=\Delta p\left[q\left(1+e_{D}\right)\right]$

ध्यान दीजिए कि

यदि $e_{D}<-1$ तो $q\left(1+e_{D}\right)<0$ तथा इस प्रकार $\Delta E$ का विपरीत चिह्न $\Delta p$ है, यदि $\mathrm{e} _{\mathrm{D}}>-1$ तो $q\left(1+e _{D}\right)>0$ तथा इस प्रकार $\Delta E$ का समान चिन्न $\Delta p$ है।

यदि $\mathrm{e} _{\mathrm{D}}=-1$ तो $q\left(1+e _{D}\right)=0$ तथा इस प्रकार $\Delta E=0$

2.7 सारांश

• बजट सेट उन वस्तुओं के सभी बंडलों का संग्रह है, जिन्हें उपभोक्ता प्रचलित बाज़ार कीमत पर अपनी आय से खरीद सकता है।
• बजट रेखा उन सभी बंडलों का प्रतिनिधित्व करती है जिन पर उपभोक्ता की सम्पूर्ण आय व्यय हो जाती है। बजट रेखा की प्रवणता ॠणात्मक होती है। यदि कीमतों या आय दोनों में से किसी एक में परिवर्तन आता है, तो बजट सेट में परिवर्तन आ जाता है।
• सभी संभावित बंडलों के संग्रह के विषय में उपभोक्ता के सुस्पष्ट अधिमान हैं। वह उन पर अपनी अधिमानता के अनुसार उनका श्रेणीकरण कर सकता है।
• उपभोक्ता के अधिमान एकदिष्ट मानी जाती है।
• अनधिमान वक्र सभी बिन्दुओं का बिन्दुपथ है जो उन बंडलों को प्रदर्शित करते हैं, जिनके बीच उपभोक्ता तटस्थ है।
• अधिमान की एकदिष्टता से अभिप्राय है कि अनधिमान वक्र की प्रवणता नीचे की ओर है।
• उपभोक्ता का अधिमान सामान्यतः अनधिमान मानचित्र द्वारा दर्शाया जा सकता है।
• उपभोक्ता का अधिमान सामान्यतः उपयोगिता फलन द्वारा भी दर्शाया जा सकता है।
• एक युक्तिशील उपभोक्ता सदा बजट सेट में से अपने सर्वाधिक अधिमानता बंडल का चयन करता है।
• उपभोक्ता का इष्टतम बंडल बजट रेखा तथा अनधिमान वक्र के बीच स्पर्शिता बिन्दु पर स्थित होता है।
• उपभोक्ता का माँग वक्र वस्तु की उस मात्रा को प्रदर्शित करता है, जिसका चयन उपभोक्ता कीमत के विभिन्न स्तरों पर ऐसी स्थिति में करता है, जब अन्य वस्तुओं की कीमत, उपभोक्ता की आय तथा उसकी रुचियाँ और अधिमान अपरिवर्तित रहते हैं।
• माँग वक्र की प्रवणता साधारणतः नीचे की ओर रहती है।
• किसी सामान्य वस्तु की माँग में वृद्धि (गिरावट) उपभोक्ता की आय में वृद्धि (गिरावट) के साथ होती है।
• उपभोक्ता की आय में वृद्धि (गिरावट) होने के साथ-साथ निम्नस्तरीय वस्तु की माँग में गिरावट (वृद्धि) होती है।
• बाज़ार माँग वक्र बाज़ार में सभी उपभोक्ताओं की माँग को वस्तु की कीमत के विभिन्न स्तरों पर समग्र दृष्टि से देखकर माँग को प्रदर्शित करता है।
• किसी वस्तु की माँग की कीमत लोच, किसी वस्तु की माँग के प्रतिशत में परिवर्तन को इसकी कीमत के प्रतिशत-परिवर्तन से भाग देकर प्राप्त किया जाता है।
• माँग की लोच एक शुद्ध संख्या है।
• किसी वस्तु के लिए माँग की लोच और उस वस्तु पर सम्पूर्ण व्यय का आपस में गहरा संबंध है।

2.8. आधारभूत संकल्पनाएँ

2.9 अभ्यास

1. उपभोक्ता के बजट सेट से आप क्या समझते हैं?

2. बजट रेखा क्या है?

3. बजट रेखा की प्रवणता नीचे की ओर क्यों होती है? समझाइए।

4. एक उपभोक्ता दो वस्तुओं का उपभोग करने के लिए इच्छुक हैं। दोनों वस्तुओं की कीमत क्रमशः 4 रुपए तथा 5 रुपए हैं। उपभोक्ता की आय 20 रुपए है:

(i) बजट रेखा के समीकरण को लिखिए।

(ii) उपभोक्ता यदि अपनी सम्पूर्ण आय वस्तु 1 पर व्यय कर दे, तो वह उसकी कितनी मात्रा का उपभोग कर सकता है?

(iii) यदि वह अपनी सम्पूर्ण आय वस्तु 2 पर व्यय कर दे, तो वह उसकी कितनी मात्रा का उपभोग कर सकता है?

(iv) बजट रेखा की प्रवणता क्या है?

प्रश्न 5,6 तथा 7 प्रश्न 4 से संबंधित है।

5. यदि उपभोक्ता की आय बढ़कर 40 रुपए हो जाती है, परन्तु कीमत अपरिवर्तित रहती है तो बजट रेखा में क्या परिवर्तन होता है?

6. यदि वस्तु 2 की कीमत में एक रुपए की गिरावट आ जाए परन्तु वस्तु 1 की कीमत में तथा उपभोक्ता की आय में कोई परिवर्तन नहीं हो, तो बजट रेखा में क्या परिवर्तन आएगा?

7. अगर कीमतें और उपभोक्ता की आय दोनों दुगुनी हो जाए, तो बजट सेट कैसा होगा?

8. मान लीजिए कि कोई उपभोक्ता अपनी पूरी आय का व्यय करके वस्तु 1 की 6 इकाइयाँ तथा वस्तु 2 की 8 इकाइयाँ खरीद सकता है। दोनों वस्तुओं की कीमतें क्रमशः 6 रुपए तथा 8 रुपए हैं। उपभोक्ता की आय कितनी है?

9. मान लीजिए, उपभोक्ता दो ऐसी वस्तुओं का उपभोग करना चाहता है जो केवल पूर्णांक इकाइयों में उपलब्ध हैं। दोनों वस्तुओं की कीमत 10 रुपए के बराबर ही है तथा उपभोक्ता की आय 40 रुपए है।

(i) वे सभी बंडल लिखिए, जो उपभोक्ता के लिए उपलब्ध है।

(ii) जो बंडल उपभोक्ता के लिए उपलब्ध हैं, उनमें से वे बंडल कौन से हैं जिन पर उपभोक्ता के पूरे 40 रुपए व्यय हो जाएँगे।

10. ‘एकदिष्ट अधिमान’ से आप क्या समझते हैं?

11. यदि एक उपभोक्ता के अधिमान एकदिष्ट हैं, तो क्या वह बंडल $(10,8)$ और बंडल $(8,6)$ के बीच तटस्थ हो सकता है?

12. मान लीजिए, कि उपभोक्ता के अधिमान एकदिष्ट हैं। बंडल $(10,10),(10,9)$ तथा $(9,9)$ पर उसके अधिमान श्रेणीकरण के विषय में आप क्या बता सकते हैं?

13. मान लीजिए कि आपका मित्र, बंडल $(5,6)$ तथा $(6,6)$ के बीच तटस्थ है। क्या आपके मित्र के अधिमान एकदिष्ट हैं?

14. मान लीजिए कि बाज़ार में एक ही वस्तु के लिए दो उपभोक्ता हैं तथा उनके माँग फलन इस प्रकार हैं:

$d_{1}(p)=20-p$ किसी भी ऐसी कीमत के लिए जो 20 से कम या बराबर हो तथा $d_{1}(p)=0$ किसी ऐसी कीमत के लिए जो 20 से अधिक हो।

$d_{2}(p)=30-2 p$ किसी भी ऐसी कीमत के लिए जो 15 से कम या बराबर हो और $d_{1}(p)=0$ किसी ऐसी कीमत के लिए जो 15 से अधिक हो।

बाज़ार माँग फलन को ज्ञात कीजिए।

15. मान लीजिए, वस्तु के लिए 20 उपभोक्ता हैं तथा उनके माँग फलन एक जैसे हैं:

$d(p)=10-3 p$ किसी ऐसी कीमत के लिए जो $\frac{10}{3}$ से कम हो अथवा बराबर हो तथा $d_{1}(p)=0$ किसी ऐसी कीमत पर $\frac{10}{3}$ से अधिक है। बाज़ार माँग फलन क्या है?

16. एक ऐसे बाज़ार को लीजिए, जहाँ केवल दो उपभोक्ता हैं तथा मान लीजिए वस्तु के लिए उनकी माँगें इस प्रकार हैं:

वस्तु के लिए बाज़ार माँग की गणना कीजिए।

17. सामान्य वस्तु से आप क्या समझते हैं?

18. निम्नस्तरीय वस्तु को परिभाषित कीजिए। कुछ उदाहरण दीजिए।

19. स्थानापन्न को परिभाषित कीजिए। ऐसी दो वस्तुओं के उदाहरण दीजिए जो एक-दूसरे के स्थानापन्न हैं।

20. पूरकों को परिभाषित कीजिए। ऐसी दो वस्तुओं के उदाहरण दीजिए, जो एक-दूसरे के पूरक हैं।

21. माँग की कीमत लोच को परिभाषित कीजिए।

22. एक वस्तु की माँग पर विचार करें। 4 रुपये की कीमत पर इस वस्तु की 25 इकाइयों की माँग है। मान लीजिए वस्तु की कीमत बढ़कर 5 रुपये हो जाती है तथा परिणामस्वरूप वस्तु की माँग घटकर 20 इकाइयाँ हो जाती है। कीमत लोच की गणना कीजिए।

23. माँग वक्र $D(p)=10-3 p$ को लीजिए। कीमत $\frac{5}{3}$ पर लोच क्या है?

24. मान लीजिए किसी वस्तु की माँग की कीमत लोच -0.2 है। यदि वस्तु की कीमत में $5 %$ की वृद्धि होती है, तो वस्तु के लिए माँग में कितनी प्रतिशत कमी आएगी?

25. मान लीजिए, किसी वस्तु की माँग की कीमत लोच -0.2 है। यदि वस्तु की कीमत में $10 %$ वृद्धि होती है, तो उस पर होने वाला व्यय किस प्रकार प्रभावित होगा?

26. मान लीजिए कि किसी वस्तु की कीमत में $4 %$ की गिरावट होने के परिणामस्वरूप उस पर होने वाले व्यय में $2 %$ की वृद्धि हो गई। आप माँग की लोच के बारे में क्या कहेंगे?