Introduction
Light is a form of energy which enables human beings and creatures to ‘see’ things. When light emitted from an object or reflected from the object enters our eyes we are able to see the object. We can’t see an object in dark even if we are in light because there is no light coming from the object to our eyes.
Light is an electromagnetic radiation which exhibits properties like a wave as well as a particle. It always propagates in a straight line and reflects, refracts or shows total internal reflection at an interface separating two media in different conditions. This chapter is an attempt to provide sufficient information to make us understand what is light, how does it propagate, how does it show reflection, refraction and total internal reflection, how does it behave with mirrors and lenses, etc.
WHAT IS LIGHT ?
Light is electromagnetic radiation, such as that emitted by the Sun, which acts like a wave in a frequency range that the human eye can perceive. At the same time, light also acts like a stream of particles, which are called photons (hence the expression “beam of light”). Electrons can be shot out of atoms and molecules can be split simply by the impact of a photon striking them. A film in a camera is exposed in this way; the light splits the silver bromide into silver and bromine. The silver darkens the-film and a negative is created. Light is a combination of electric and magnetic oscillations in mutually perpendicular directions as shown in Fig. 1.1. But the light wave itself propagates in a direction perpendicular to both the oscillations.

Look at fig. Which line do you think is the langer? Measure the twa lines ta prove that they are, in fact, equal in length. Why da you think the lower line ’looks’ langer than the upper line?

OPTICS
The branch of physics which deals with the propagation, nature and behavior of light is known as optics. The different branches of optics and the behavior of light falling under that branch can best be illustrated by the following diagram.
PROPERTIES OF LIGHT
(1) Light travels along a straight line in a medium or vacuum. The path of light changes only when the medium changes. This is also called the rectilinear propagation of light.
(2) Light travels with a speed nearly equal to
(3) Light shows different behavior such as reflection, refraction, interference, diffraction, polarization etc. some of which we will deal with subsequently in this book and some in higher classes.
RAY OF LIGHT
Let us consider a source of light(s). Also consider the light which passes from the point A to the point 
Fig. 1.2 AB is a ray of light in a medium
BEAM OF LIGHT
A bundle of light rays is called a beam of light. The following figure shows a parallel beam of light.
Fig. 1.3 A parallel beam of light.
CHECK POINT
A person in a dark room looking through a window can clearly see a person outside in the daylight, whereas the person outside cannot see the person inside. Explain.
Show Answer
SOLUTION
When a person inside a darkroom is looking through a window to another person outside in broad daylight, then enough reflected rays come inside to the eye of the observer from the person outside. So he can be seen clearly. But if the person in daylight, looks through the same window to the person inside the dark room, there is hardly any reflected rays coming from the body of the person inside the dark room to the eyes of the observer outside. So the outside observer can’t see the person inside the room.
REFLECTION AND REFRACTION OF LIGHT
Most of the things we see around us do not emit their own light. They are visible because they reemit light reaching their surface from a primary source, such as the sun or a lamp, or from a secondary source, such as the illuminated sky. When light falls on the surface of a material, it is usually either reemitted without change in frequency or is absorbed into the material and turned into heat. Usually, both of these processes occur in varying, degrees. When the reemitted light is returned into the medium from which it came, it is reflected, and the process is referred to as reflection. When the reemitted light bends from its original course and proceeds in straight lines from molecule to molecule into a transparent material, it is refracted, and the process is referred to as refraction.
REFLECTION
When this page is illuminated by sunlight or lamplight, electrons in the atoms of the paper vibrate more energetically in response to the oscillating electric fields of the illuminating light. The energized electrons reemit the light by which we see the page. When the page is illuminated by white light, it appears white, which reveals the fact that the electrons reemit all the visible frequencies. Very little absorption occurs. The ink on the page is a different story. Except for a bit of reflection, the ink absorbs all the visible frequencies and therefore appears black. The following figure shows reflection of a building in the sea.

Fig. 1.4 Image of a building in the sea due to reflection of light
LAWS OF REFLECTION
Anyone who has played pool or billiards knows that, when a ball bounces from a surface, the angle of incidence is equal to the angle of rebound. The same is true of light. This is the law of reflection, and it holds for all angles:
The angle of reflection equals the angle of incidence.
The law of reflection is illustrated with to s representing light rays in Fig. 1.5 Instead of measuring the angles of incident and reflected rays from the reflecting surface, it is customary to measure them from a line perpendicular to the plane of the reflecting surface. This imaginary line is called the normal. The incident ray, the normal, and the reflected ray all lie in the same plane.
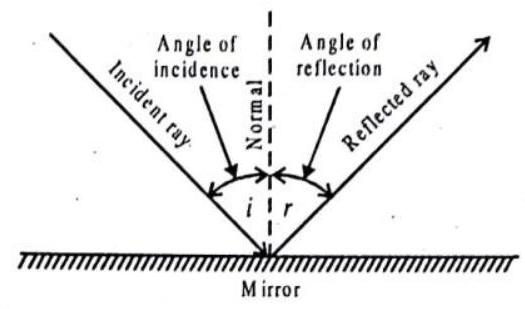
Fig.1.5 According to the law of reflection
So, we can summaries the laws of reflection as below :
1. The angle of incidence
2. The incident ray, the normal, and the reflected ray all lie in the same plane.
1. Law of reflection are applicable for plane surfaces as well as curved surfaces.

2. Most people are surprised by the fact that light can be reflected back from a less dense medium. For instance, if you are diving and you look up at the surface of the water, you will see a reflection of yourself.
CHECK POINT
- Each of these diagrams numbered 1,2 and 3 is supposed to show two different rays being reflected irom the same point on the same mirror. Which are correct, and which are incorrect ?

SOLUTION
Only 1 is correct. Draw the normal that bisects the solid ray, it also bisects the dashed ray.
SPECULAR AND DIFFUSE REFLECTIONS
When light is incident on a smooth surface it is reflected in the first medium. This reflection on a smooth surface is called specular reflection. When light is incident on a rough surface, it is reflected in many directions. This is called diffuse reflection. If the surface is so smooth that the distances between successive elevations on the surface are less than about one-eighth the wavelength of the light, there is very little diffuse reflection, and the surface is said to be polished. A surface therefore may be polished for radiation of long wavelengths but rough for light of short wavelengths. The wire-mesh “dish” shown in fig. 1.7 is very rough for light waves and is hardly mirror like. But, for long-wavelength radio waves, it is “polished” and is an excellent reflector.
Light reflecting from this page is diffusion. The page may be smooth to a radio wave, but, to a light wave, it is rough. Smoothness is relative to the wavelength of the illuminating waves. Rays of light striking this page encounter millions of tiny flat surfaces facing in all directions. The incident light, therefore, is reflected in all directions.
This is a desirable circumstance. It enables us to see objects from any direction or position. You can see the road ahead of your car at night, for instance because of diffuse reflection by the rough road surface. When the road is wet, however, it is smoother with less diffuse reflection, and therefore more difficult to see. Most of our environment is seen by diffuse reflection.
Fig. 1.6 Diffuse reflection. Although reflection of each single ray obeys the law of reflection, the many different surface angles that light rays encounter in striking a rough surface produce reflection in many directions.

Fig. 1.7 The open-mesh parabolic dish is a diffuse reflector for short-wavelength light but a polished reflector for long-wavelength radio waves.
ILLUSTRATION-1.1
Twn mirrors make an angle of
Show Answer
SOLUTION:
From the law of reflection, we know that the first reflected ray also makes an angle of

Fig. 1.8 Mirrors
CHECK POINT
An observer on the west-facing beach of a large lake is watching the beginning of a sunset. The water is very smooth except for some areas with small ripples. The observer notices that some areas of the water appear blue and some appear pink. Why does the water appear to be different colors in different areas?
Show Answer
SOLUTION
The different colors arise from specular and diffuse reflection. The smooth areas of the water specularly reflect the light from the west, which is the pink light from the sunset. The areas with small ripples reflect the light diffusely. Thus, light from all parts of the sky is reflected into the observers’ eyes. Because most of the sky is still blue at the beginning of the sunset, these areas appear to be blue.
REVERSIBILITY OF LIGHT RAYS:
The fact that specular reflection displays equal angles of incidence and reflection means that there is a symmetry: if the ray had come in from the right instead of the left in the figure above, the angles would have looked exactly the same. This is not just a pointless detail about specular reflection.
It’s a manifestation of a very deep and important fact about nature, which is that the laws of physics do not distinguish between past and future. Cannonballs and planets have trajectories that are equally natural in reverse, and so do light rays. This type of symmetry is called time-reversal symmetry. Typically, time-reversal symmetry is a characteristic of any process that does not involve heat. For instance, the planets do not experience any friction as they travel through empty space, so there is no frictional heating.
We should thus expect the time-reversed versions of their orbits to obey the laws of physics, which they do. In contrast, a book sliding across a table does generate heat from friction as it slows down, and it is therefore not surprising that this type of motion does not appear to obey time-reversal symmetry. A book lying still on a flat table is never observed to spontaneously start sliding, sucking up heat energy and transforming it into kinetic energy.
Similarly, the only situation we’ve observed so far where light does not obey time-reversal symmetry is absorption, which involves heat. Your skin absorbs visible light from the sun and heats up, but we never observe people’s skin to glow, converting heat energy into visible light. People’s skin does glow in infrared light, but that doesn’t mean the situation is symmetric. Even if you absorb infrared, you don’t emit visible light, because your skin isn’t hot enough to glow in the visible spectrum.
REFLECTION AT A PLANE MIRROR
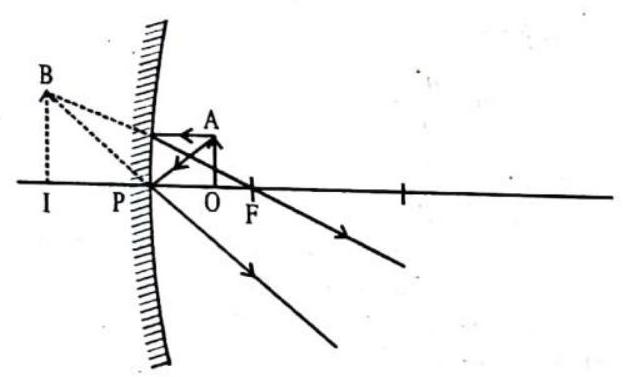
Let’s apply ray-diagram methods to the case of an object in front of a plane mirror in order to determine the position of the image of that object. Here’s the configuration.
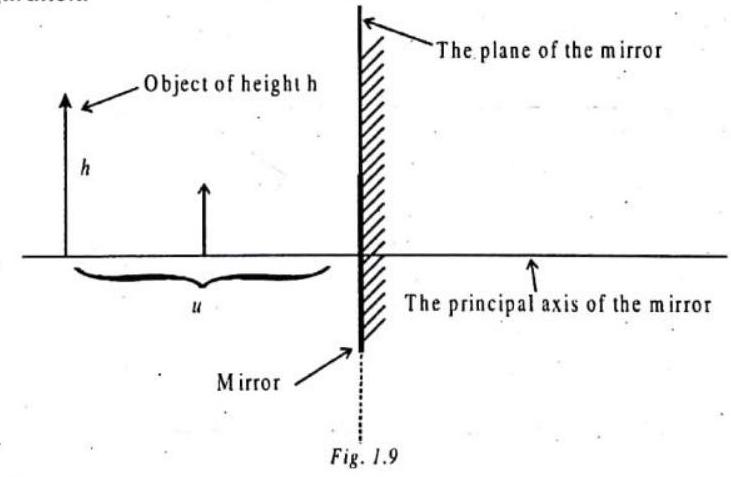
We have an object of height h, a distance
We use the method of principal rays to determine the position of the image of the object. In the method of principal rays, we consider only a few incident rays for which the reflected rays are particularly easy to determine. Experimentally, we find that the position of the image is independent of the size of the mirror, so we consider the mirror to be as large as it needs to be for the principal rays to hit it. In particular, if a principal ray appears to miss the mirror in our diagram, we show the ray as reflecting off the plane of the mirror nevertheless. Our Principal Ray I for the case at hand is one that approaches the plane of the mirror along a line that is parallel to the principal axis of the mirror.

According to the law of reflection. Principal ray

Principal ray II hits the mirror right where the principal axis of the mirror intersects the mirror. In accord with the Law of Reflection, with, for the ray in question, the principal axis of the mirror being the normal, the reflected ray makes the same angle with the principal axis of the mirror as the incident ray does.
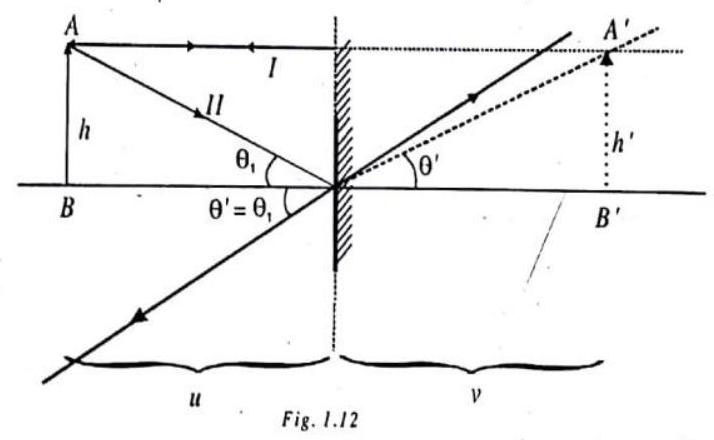
Tracing back the second reflected ray, to the point where it intersects the first reflected ray traceback line, yields the position of the image of the tip of the to. The image height
Thus the right triangle of side
Hence, since corresponding sides of congruent triangles are equal, we have
Characteristics of image formed by plane mirror :
1. Distance of object from mirror
2. The image is laterally inverted (better word perversion).
3. The line joining the object point with its image is normal to the reflecting surface.
4. The size of the image is the same as that of the object.
(i) For a real object the image is virtual and for a virtual object the image is real.

(ii) If keeping the incident ray fixed, the mirror is rotated by an angle

1. If two plane mirrors are kept inclined to each other at angle
All this is given below in a tabular form :
| S.No. | No. of images formed if object is placed | ||||
|---|---|---|---|---|---|
| 1 | 0 | ||||
| 2 | 30 | 12 | 11 | 11 | |
| 3 | 45 | 8 | 7 | 7 | |
| 4 | 60 | 6 | 5 | 4 | |
| 5 | 72 | 5 | 4 | 4 | |
| 6 | 75 | 4.8 | 3 | 3 | |
| 7 | 90 | 4 | 3 | 3 | |
| 8 | 112.5 | 3.2 | 3 | 2 | |
| 9 | 120 | 3 |
(a) If an object is placed between two parallel mirrors
(b) The number of images formed by two mutually perpendicular mirrors
(c) Two mirrors inclined to each other at different angles may provide same number of images, e.g., for any value of
(d) The number of images seen may be different from the number of images formed and depends on the position of observer relative to object and mirrors - e.g., if
2. If an object moves towards (or away from) a plane mirror at speed
3. To locate the image of an object from an inclined mirror, see the perpendicular distance of the object from the mirror.

4. If angle between two mirrors is

Fig. 1.76
CHECK POINT
We see the bird and its reflection. Why do we not see the bird’s feet in the reflection?
Show Answer
SOLUTION
The bird’s feet are on the reflecting surface so the image of feet is formed at the same place where actually the feet are. So the image of the feet cannot be distinguished from the actual feet. This is so because the distance of the object from the reflecting surface is equal to that of the image from same surface.

ILLUSTRATION-1.2
Find the minimum height of a mirror where one can see his full image.
Show Answer
SOLUTION:
Let
we have,
Now,
So the required height of the mirror be half of the height of the person.

ILLUSTRATION-1.3
Two plane mirrors are inclined at an angle
Show Answer
SOLUTION:
The situation is illustrated in fig. 1.19.
Then from
or
Thus if the angle of incidence is

ILLUSTRATION-1.4
Find the

Show Answer
SOLUTION:
Image of
REFLECTION AT CURVED SURFACES
Mirrors : Mirrors can be found in every home, office, and public place. Without these simple instruments, doing many activities would be difficult or impossible. Mirrors can take on various forms depending on the purpose for which they are designed. For example, the rearview mirror of a vehicle does not provide much detail. Of more importance is that it indicates the position of other cars in as large an area as possible.
Types of Mirrors : In a bathroom mirror, we normally see ourselves in actual size, and the surface is flat. In a mirror that is sometimes used for shaving, the face appears very large. If we back up, though, after a moment of confusion, we appear small and in a reversed position. The surface is a spherical shape seen from the inside (concave). In automobile rearview mirrors, the images often appear small, but you can see over a large area. Their surface is also curved, but the image is seen from the outside (convex).
Flat Mirrors
When we place in object in front of a flat mirror, we see it as if it were located behind the mirror and in specular symmetry. This means that the image produced is the same as the object but with left and right reversed. As they are reflected, the light rays reach our eyes and we see the object in the prolongation of these rays.
Concave Mirrors
Imagine a sphere of hollow glass. If we cut out a spherical cap and plate it with silver on the outside, we have a concave mirror if we look at it from the hollow side. These mirrors, a spherical cap and plat convergent mirrors, concentrate the light rays, causing them to arrive parallel to the main axis onto a point known as the focal point. Concave mirrors form real images that can be projected onto a screen if the object is farther away than the focal point. The image obtained is large if formed near the focal point or small if formed far away from the focal point. In both cases, the image is reversed. If we place the object closer than the focal point, the image is formed upright and large but virtual (i.e., it cannot be projected).
Convex Mirrors
If we plate the inner surface of a concave mirror with silver and look at it toward the outward bulge, we have a convex mirror. Mirrors of this type are also called divergent mirrors because the light beams that reach their surface and are parallel to their main axis are diverted in such a way that they separate, but their extensions come back together again in a point known as the focal point. The images produced by a convex mirror are always virtual, upright, and small.
TERMS RELATED TO SPHERICAL MIRROR
Centre of Curvature
Radius of Curvature
Pole
Principal Axis : It is the straight line joining the centre of curvature to the pole.
Focus
Focal Length (f): It is the distance the pole and the principal focus. For spherical mirrors,
RULES FOR RAY DIAGRAMS
(i) When a ray falls in the direction of centre of curvature of mirror then it reflects back along the same path.
(ii) A ray, parallel to the principal axis will after reflection, pass through the focus.
(iii) A ray, passing through the focus is reflected parallel to the principal axis.
Observe the following diagrams to draw ray diagrams.

REFLECTION THROUGH CONCAVE MIRROR
When a narrow beam of light trayelling parallel to the principal axis is incident on the reflecting surface of the concave mirror, the beam after reflection converge at a point on the principal axis.
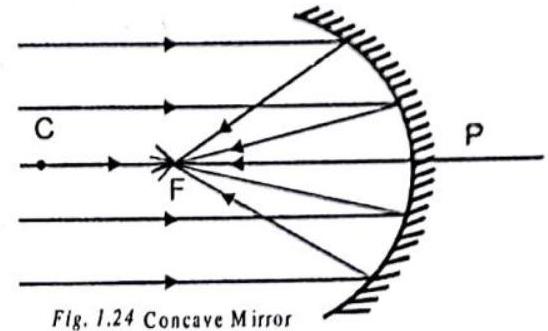
IMAGE FORMED BY THE CONCAVE MIRROR
| Position of object | Position of image | Nature | Figure |
|---|---|---|---|
| At infinity | At the focus | Real, inverted & diminished | |
| Between infinity & Centre of Curvature | Between focus & centre of curvature | Real, inverted & small in size | |
| At centre of curvature | At centre of curvature | Real, inverted and of the same size | |
| Between Focus & centre of curvature | Beyond centre of curvature | Real, inverted and enlarged | |
| At Focus | At infinity | Real, inverted and very large | |
| Between Focus & Pole | Behind the mirror | Erect, virtual & enlarged |
Makeup and shaving mirrors are concave mirrors. When you place your face between the mirror and its focal point, you see an enlarged virtual image of yourself. Concave mirrors are also used in a new method for displaying the speed of a car.
REFLECTION THROUGH CONVEX MIRROR
When a narrow beam of light travelling parallel to the principal axis is incident on the reflecting surface of the mirror, the beam after reflection appear to diverge from a point on the principal axis. When a ray incident on convex mirror in the direction of centre of curvature after reflection comes back along the same path. When a ray incident on convex mirror parallel to the principal axis, after reflection, appears to come from the focus. A ray appearing to pass through the focus is reflected parallel to the principal axis.
IMAGE FORMED BY CONVEX MIRROR
A convex mirror forms only virtual images for all positions of the real object. The image is always virtual, erect, smaller than the object and is located between the pole & the focus. The image becomes smaller and moves closer to the focus as the object is moved away from the mirror.

The virtual image is diminished in size and upright, relative to the object. A convex mirror form a virtual image of the object, no matter where in front of the mirror the object is placed. Because of the shape of convex mirrors, they give a wider field of view than do other types of mirrors. Therefore, they are often used for security purposes, as in figure.

Fig. 1.27 : Security mirror
A mirror with a wide field of view is also needed to give a driver a good rear view. Thus, the outside mirror on the passenger side is often a convex mirror. Printed on such a mirror is usually the warning “vehicles in mirror are closer than they appear.”

Fig. 1.28 : Rear view mirror
The reason for the warning is that the virtual image in figure is reduced in size and therefore looks smaller, just as a distant object would appear in a plane mirror. An unwary driver, thinking that the side-view mirror is a plane mirror, would appear in a plane mirror. An unwary driver, thinking that the side-view mirror is a plane mirror, might incorrectly deduce from the small size of the image that the car behind is far enough away to ignore.
COMPARING THE FIELDS OF VIEW OF A PLANE MIRROR AND A CONVEX MIRROR
For a fair comparison to be made the two mirrors must be the same size and the eye must be placed at the same distance from each of them. The maximum angle of view is obtained when the angle of reflection at the mirror is a maximum, i.e., when the normal to the mirror are drawn at the extreme edges of the mirror.
The normals to the convex mirror are lines which are continuations of the radii at the edges of the mirror. Once the angles of reflection have been drawn, equal angles must be drawn on the other side of the normals to give the position of the incident rays. The angle of incidence for the convex mirror is much greater than the angle of incidence for the plane mirror, hence the convex mirror has a greater field of view that the plane mirror.

Fig. 1.29
SIGN CONVENTION
(1) All distances are measured from the pole.
(2) The distance measured along the direction of propagation of light are taken as positive and the direction opposite to the propagation of light is taken as negative.
(3) The distances (heights) measured above the principal axis i.e. along positive
Note that in this convention, the focal length
The sign convention can be summarized in the following figure.

Note : Many Students get confused in applying sign convention and a small error in sign of one variable will throw all your calculation. Please study 3 points carefully ( put known quantities with proper sign unknown quantity will come automatically with proper sign).
In following situations, the sign convention has been applied.
1. Consider the mirror shown in Fig. 1.31 (a). Here, the object is on the left and image is also on the left. The mirror is a concave mirror. The incident ray is directed from left to right and so the positive
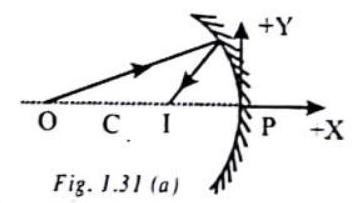
2. Consider the mirror shown in Fig. 1.31 (b). Here, the object is on the left and image is on the right and the mirror concave. The incident ray is once again from left to right and so the positive
Here, Object distance

3. Consider the mirror shown in Fig. 1.31 (c). Here, the object is virtual and on the left, image is also on the right and the mirror is a convex. The incident ray is from the right and the positive
Focal length

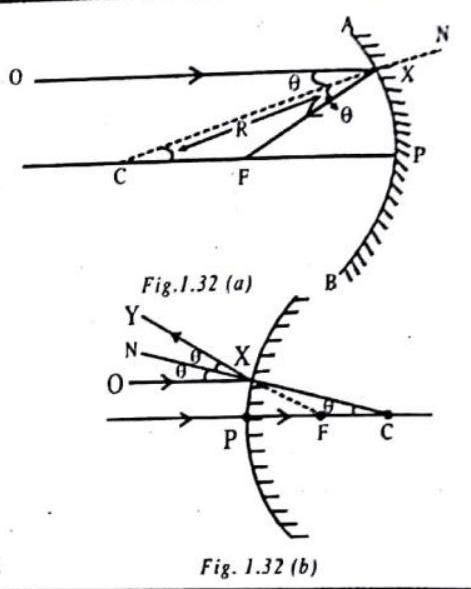
RELATION BETWEEN FOCAL LENGTH (
4. Proof : In Fig. 1.32, incident ray
For concave mirror (Fig.1.32 (a) (because
But
For convex mirror (Fig. 1.32 (b)
But
and
Hence (in both cases),
For mirror of small aperture,
Hence,
CHECK POINT
Her eye at point
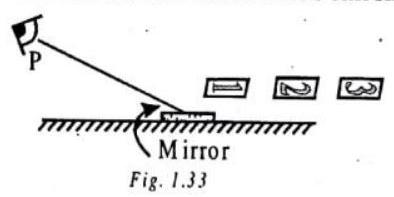
Show Answer
SOLUTION
Card number 2, she can see through the mirror. According to law of reflection, angle of incidence is equal to angle of reflection. Light ray coming from card number 2 makes the same angle with the normal at the point of incidence as the light ray going to eye makes with the normal.
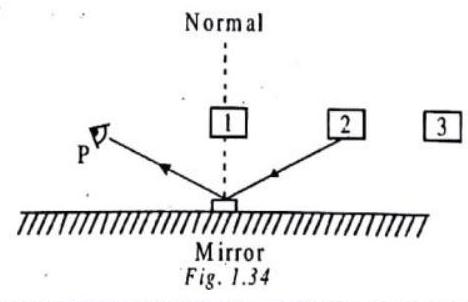
ILLUSTRATION-1.5
The radius of curvature of a spherical mirror is
Show Answer
SOLUTION:
MIRROR FORMULA
A relationship among the object distance
Proof: Take an object
Draw
In
In
But
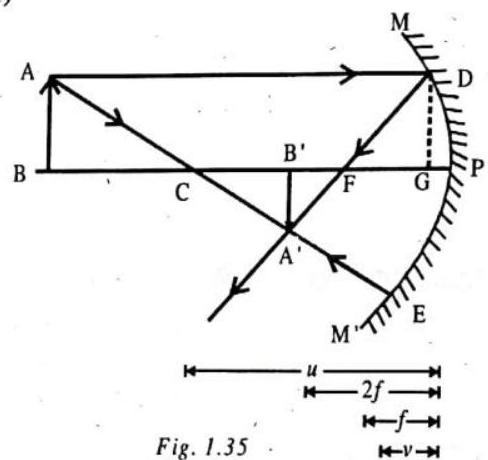
From (1) and (2), we get,
Let us assume that mirror is very small,
From (3),
Dividing both sides by
ILLUSTRATION-1.6
An object is placed at a distance of
Show Answer
SOLUTION:
Given
Using the mirror formula
Hence, the image is formed at a distance of
ILLUSTRATION- 1.7
We wish to obtain an erect image of an object, using a concave mirror of focal length
Show Answer
SOLUTION:
For getting an erect image using a concave mirror the object should be placed at a distance less than the focal length (i.e.)

ILLUSTRATION-1.8
A concave mirror and a convex mirror are placed co-axially, their reflecting surfaces facing each other. Their focal lengths are 15 and
Show Answer
SOLUTION:
In a concave mirror for the image to be formed at the object itself, the latter must be at the centre of curvature. But here, it is at a distance of
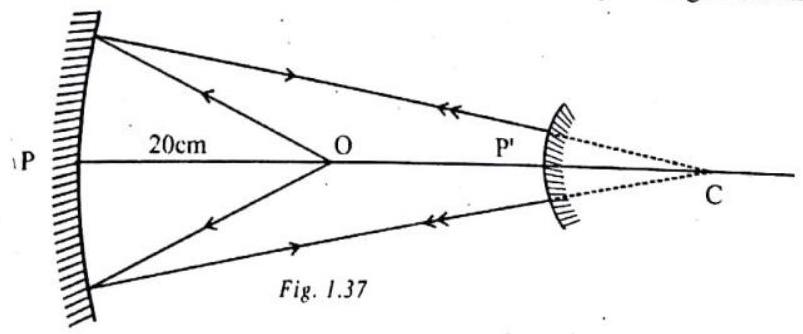
The reflected rays from concave mirror are reflected back by convex mirror.
But we want
Now
MAGNIFICATION
If the mirror is plane, the size of the image is always equal to the size of the object. But the case is different for a curved mirror. The size of the image is different from the size of the object is such a ‘mirror’. Image may be greater or smaller in size than the object depending upon the nature of the mirror or the location of the object.
Let
Here
OTHER FORMULAE OF MAGNIFICATION
We have
By mirror formula,
Dividing both sides, of (2) by
From(1)&(3),
Dividing both sides of (2) by
From(1) and (5),
ILLUSTRATION-1.9
An object,
Show Answer
SOLUTION:
Object-size,
Image-distance,
From
or
The screen should be placed at
Also, magnification,
Height of the image,
The image is inverted and enlarged.
ILLUSTRATION-1.10
A convex mirror used for rear-view on an automobile has a radius of curvature of
Show Answer
SOLUTION:
Radius of curvature,
Focal length,
Since
The image is
Magnification,
The image is virtual, erect and smaller in size by a factor of 0.23 .
ILLUSTRATION-1.11
An object of size
Show Answer
SOLUTION:
Using,
Using
Since
Since
ILLUSTRATION-1.12
A concave makeup mirror is designed so the virtual image is twice the size of the object, when the distance between the object
and mirror is
Show Answer
SOLUTION:
The magnification is,
Therefore, the focal length is found from
ILLUSTRATION-13
The image of an object viewed in a concave mirror of focal length
Show Answer
SOLUTION:
We have,
The magnification is,
ILLUSTRATION-1.14
A concave mirror of focal length
Show Answer
SOLUTION:
ILLUSTRATION-1.15
The focal length of a concave mirror is
Show Answer
SOLUTION:
Here image can be real or virtual. If the image is real
If the image is virtual
ILLUSTRATION-1.16
The sun (diameter
Show Answer
SOLUTION:
Since the sun is very distant,
The image of sun will be formed at the focus and will be real, inverted and diminished
POWER OF A MIRROR
The power of a mirror is defined as its capacity to converge or diverge. Mathematically, it is defined as inverse of focal length. For concave mirror power is positive as it is a converging mirror and for convex it is negative as it is a diverging mirror.
The unit of power is diopter.
In sign convention,
NEWTON’S FORMULA
This formula provides a relationship among the focal length (f), the distance of the object from focus
This can be expressed as
Note that here the object distance and the image distance are measured from the focus of the mirror not from the pole.
IDENTIFICATION OF MIRROR BY THE SIZE AND NATURE OF THE IMAGE
(i) If object and image are of same nature (i.e. both on the same side of the mirror) then they will be inverted.
(ii) If the object and image are on the opposite sides of the mirror then image is erect relative to object.
For real extended object if the image formed by a single mirror is erect it is always virtual (i.c.
| Smaller than object, the mirror is convex | Equal to object, the mirror is plane | Larger than object, the mirror is concave |
So, by observing the size of erect imaye in a mimor we can devide the nature of the mimor i.e. Whether it is convex, concave or plane. For real extended object if the image formed by a single mimor is inverted it is always real (i.e.,
| Smaller than object, object is between the image is between |
Equal to object. object is at and image is at |
Larger than object, object is between between |
as every part of a mirror forms complete image, if a part of mirror (say half) is abstracted (say covered with Mack paper) full image will be formed fut intensity will be reduced.

REFRACTION AT PLANE SURFACES
The bending of the light ray from its path in passing from one medium to the other medium is called refraction of light.
If the refracted ray bends towards the normal relative to the incident ray, then the second medium is said to be denser than the first medium. But if the refracted ray bends away from the normal, then the second medium is suid to be rarer than the first medium.

To gain a better understanding of the bending of light in refraction. look at the pair of toy cart wheels in Fig. 1.40 (c). The wheels roll from a smooth sidewalk onto a grass lawn. If the wheels meet the grass at an angle, as the Fig. 1.40 (c), shows they are deflected from their straightline course. Note that the left wheel slows first when it interacts with the grass on the lawn. The right wheel maintains its higher speed while on the sidewalk. It pivots about the slower-moving left wheel because it travels farther in the same time. So the direction of the rolling wheels is bent tow ard the “normal,” the black dashed line perpendicular to the grass-sidewalk border in figure.

Fig. 1.41 (a) shows how a light wave bends in a similar way. Note the direction of light, indicated by the \to (the light ray). Also note the wave fronts drawn at right angles to the ray. (If the light source were close, the wave fronts would appear circular; but, if the distant sun is the source, the wave fronts are practically straight lines.) The wave fronts are everywhere at right angles to the light rays. In the Fig. 1.41 (b), the wave meets the water surface at an angle. This means that the left portion of the wave slows down in the water while the remainder in the air travels at the full speed of light, 
Fig.1.41. The direction of the light waves changes when one part of the wave slows down before the other part.
Fig. 1.42, shows a beam of light entering water at the left and exiting at the right. The path would be the same if the light entered from the right and exited at the left. The light paths are reversible for both reflection and refraction. If you see someone’s eyes by way of a reflective or refractive device, such as a mirror or a prism, then that person can see you by way of the device also.
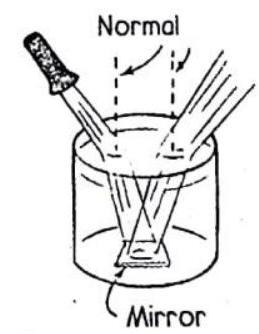
Fig.1.42. When light slows down in going from one medium to another, as it does in going from air to water it bends toward the normal. When it speeds up in traveling from one medium to another.
Refraction causes many illusions. One of them is the apparent bending of a stick that is partially submerged in water. The submerged part appears closer to the surface than it actually is. The same is true when you look at a fish in water. The fish appears nearer to the surface and closer than it really is (Fig. 1.43). If we look straight down into water, an object submerged 4 meters beneath the surface appears to be only 3 meters deep. Because of refraction, submerged objects appear to be magnified.
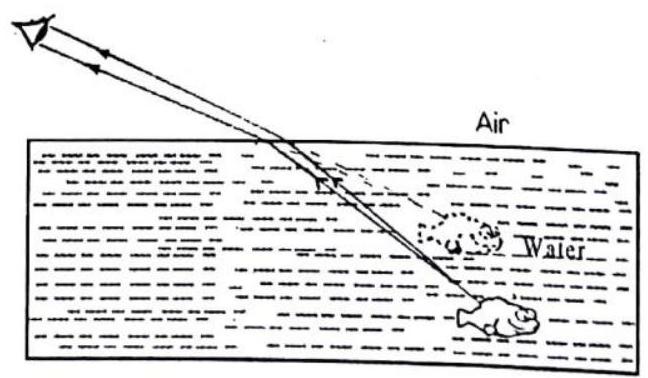
Fig.1.43 Because of refraction, a submerged object appears to be nearer to the surface than it actually is
Refraction occurs in the earth’s atmosphere. Whenever we watch a sunset, we see the sun for several minutes after it has sunk below the horizon (Fig. 1.44). The earth’s atmosphere is thin at the top and dense at the bottom. Because light travels faster in thin air than in dense air, parts of the wave fronts of sunlight at high altitude travel faster than parts closer to the ground. Light rays bend. The density of the atmosphere changes gradually, so light rays bend gradually and follow a curved path. So we gain additional minutes of daylight each day. Furthermore, when the sun (or moon) is near the horizon, the rays from the lower edge are bent more than the rays from the upper edge. This shortens the vertical diameter, causing the sun to appear elliptical figure).
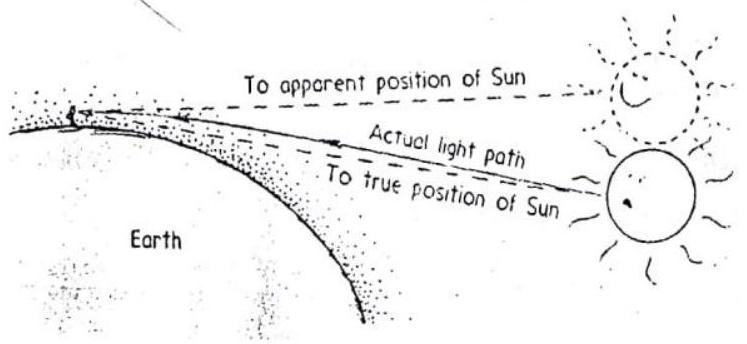
Fig. 1.44. Because of atmospheric refraction, when the sun is near the horizon it appears to be higher in the sky.

Fig. 1.45. The sun is distorted by differential refraction.
REFRACTIVE INDEX
Light travels through a vacuum at a speed
To describe the extent to which the speed of light in a material medium differs from that in a vacuum, we use a parameter called the index of refraction (or refractive index).
ABSOLUTE REFRACTIVE INDEX
It is defined as the ratio of speed of light in free space
i.e.
It is a scalar and has no units and dimensions.
As in vacuum or free space, speed of light of all wavelengths is maximum and equal to
For a given light, denser is the medium, lesser will be the speed of light and so greater will ie the refractive index, e.g. as
i.e. for a given light refractive index depends on nature of medium [i.e.,
For a given medium (other than free- space), the speed of light of different wavelengths is different, i.e.,,
As for light in free space
i.e., for a given light and medium refractive index is equal to the ratio of wavelength of light in firee space to that in the medium. Refractive index decreases with the increase in temperature.
RELATIVE REFRACTIVE INDEX
When light passes from one medium to the other, the refractive index of medium 2 relative to 1 is written as
while using the concept of relative
Usually ’
In lens theory
CHECK POINT
If, while standing on the bank of a stream, you wished to spear a fish swimming in the water out in front of you, would you aim above, below, or directly at the observed fish to make a direct hit? If you decided instead to zap the fish with a laser, would you aim above, below, or directly at the observed fish? Defend your answer.
Show Answer
SOLUTION
When you try to hit the fish with a spear, you need to aim below as the fish is actually at a lower depth than that observed by you from outside the water due to refraction of light.
When you aim with a laser light then also you should aim much below as the path of laser will change as it enters in water. Since it is going from rarer to denser medium, it bends towards the normal and deviates from the original path.
If
ILLUSTRATION-1.17
Light waves of
Show Answer
SOLUTION:
If velocity of light in vacuum is
wavelength of light in medium is
ILLUSTRATION-1.18
The refractive index of water is
Show Answer
SOLUTION:
Let the 3 media be 1,2 and 3, 1 for air, 2 for water, 3 for glass in that order.
Given :
Now using the formula,
CAUCHY’S RELATION
It gives relation between refractive index (u) and wavelength (
where A and B are constants. Thus
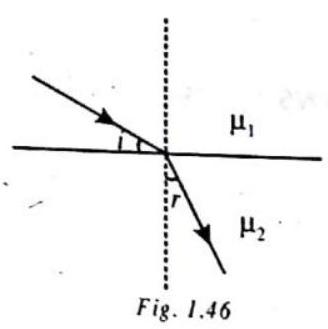
LAWS OF REFRACTION
1. The incident ray, the refracted ray and the normal to the refracting surface at the point of incidence are in the same plane.
2. The angle of incidence and the angle of refraction satisfy the equation (you can refer to Fig. 1.46)
If the speed of light were the same in all media, refraction would not accur whien light passes fram ane medium to another
CHECK POINT
If you place a glass test tube in water, you will be able to see the tube. If you place it in clear soybean oil, you may not be able to see it. What does this tell you about the speed of light in the oil and in the glass?
Show Answer
SOLUTION
If a glass test tube is placed in water and it can be seen, this indicates the speed of light in glass and water is different. So refraction takes place.
When the same glass tube is placed in soyabean oil, it cannot be seen that means the speed of light is same in both oil and glass. So no refraction takes place between the two media.
ILLUSTRATION-1.19
The refractive index of a material is 1.33 . If velocity of light in vacuum is
Show Answer
SOLUTION:
ILLUSTRATION-1.20
The angle of incidence in air for a ray of light is
Show Answer
SOLUTION:
SNELL’S LAW
For any two media and for light of a given wavelength, the ratio of the sine of the angle of incidence to the sine of the angle of refraction is a constant.
APPLICATION OF SNELL’S LAW
When light passes from rarer to denser medium it bends toward the normal. Using Snell’s Law
Thus, if

When light passes from denser to rarer medium it bends away from the normal.
Thus, if
When light propagates through a series of layers of different medium, then according to Snell’s law 
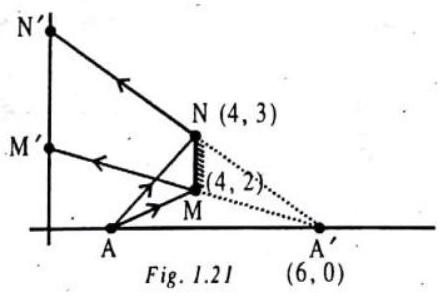
ILLUSTRATION-1.21
Light reflected from a fish strikes the surface of the water at an angle of
Show Answer
SOLUTION:
Snell’s law gives,
ILLUSTRATION-1.22
A laser beam is directed at an angle
Show Answer
SOLUTION:
Snell’s law gives for the refraction into the block
If the beam is totally internally reflected at the adjacent face, the incident angle on that face must be at least
Since the block is rectangular,
The sine function cannot be greater than one, so the angle,
ILLUSTRATION-1.23
Light strikes an interface between two materials of refractive indices
Show Answer
SOLUTION:
Snell’s law gives for any light ray
If
If
ILLUSTRATION-1.24
One light wave is incident upon a plate of refractive index
Show Answer
SOLUTION:
Angle between refractive & reflective waves
Conditions of no refraction
If light is incident normally on a boundary i.e.,
If the refractive indices of two media are equal i.e., if,
Then from Snell’s law
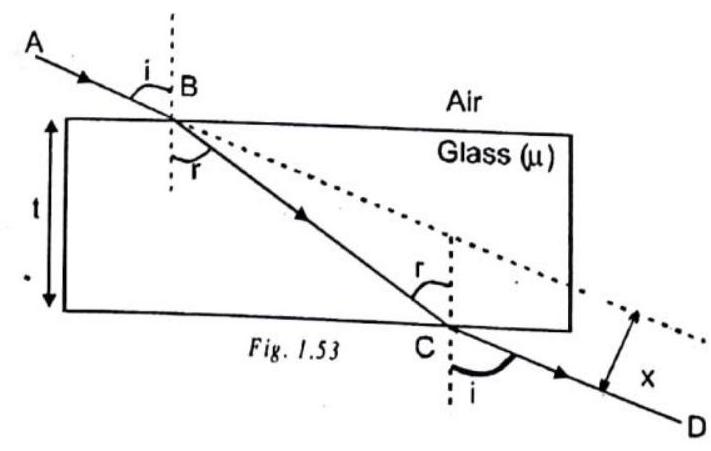
REFRACTION THROUGH A GLASS SLAB
Let us consider a glass slab of thickness
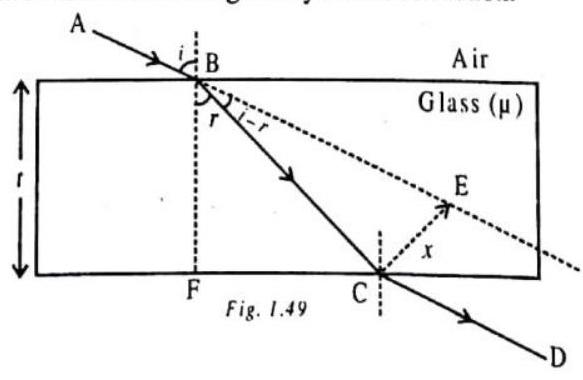
From
Also, from
| Physics |.
Equating
Lateral displacement depends an the following factors.
(i) Refractive index of the medium
(ii) Shickness of the medium (
(iii) Angle of incidence (i)
(iv) Wavelength of light
ILLUSTRATION-1.25
Figure 1.50, shows the path of ray of light passing through a glass slab. By geometrical construction calculate the refractive index of glass applying Snell’s law.
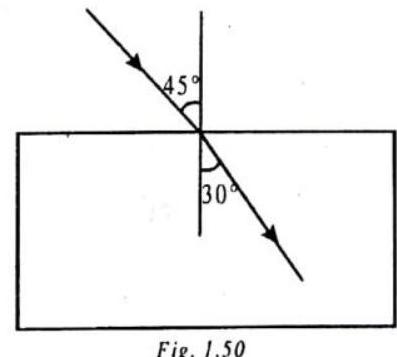
Show Answer
SOLUTION:
Refractive index
REAL AND APPARENT DEPTHS
When an object is seen from other medium, we don’t see its actual depth or height. The depth we see is called apparent depth and the actual depth is called the real depth.

Let us consider an object
Two rays
If
Let us now calculate the shift
If
By Snell’s law,
Clearly,
Case I: If
Now, shift in image
where
NOTE : If the object is placed in a medium which consists of a number of media of refractive indices
Virtual displacement
Case II : If
Case III : When object & observer both are in rarer medium.
Let observer is in air & object is at a point
Virtual displacement
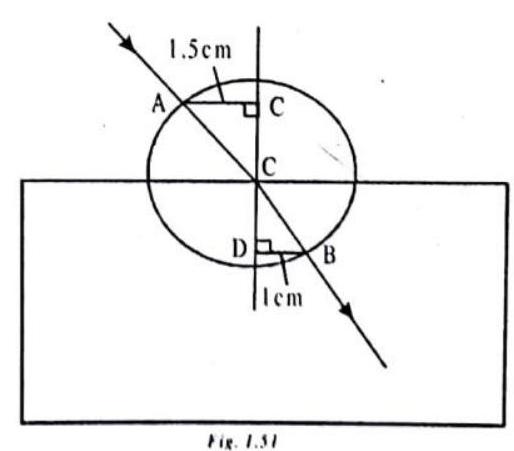
ILLUSTRATION-1.26
When a glass slab is placed on a dot on a paper, it appears displaced by
Show Answer
SOLUTION
We know that Displacement
LENS
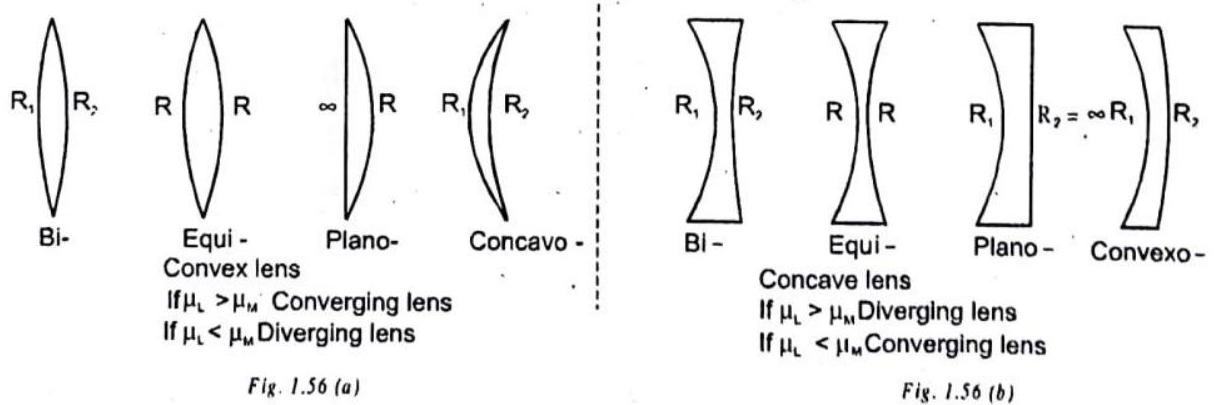
A lens is a piece of transparent material with two refracting surfaces such that at least one is curved and refractive index of used material is different from that of the surroundings.
A thin spherical lens with refractive index greater than that of surrounding behaves as a convergent or convex lens i.e. converges parallel rays. Its central (i.e. paraxial) portion is thicker than marginal one.
However if the central portion of a lens (with
TERMS RELATED TO THIN SPHERICAL LENS
Optical centre
Principal Axis

Principal Focus
A lens has two surfaces and hence two focal points first focal point is an object on the principal axis for which image is at infinity while

Second focal point is an image point on the principal axis for which object is at infinity.

Focal Length
It is defined as the distance between optical centre of a lens and the point where the parallel beam of light converges or appear to converge i.e., focus.
Aperture
In reference to lens, aperture means to effective diameter of its light transmitting area so that brightness i.e. intensity of image formed by a lens which depends on the light passing through the lens will depend on the square of aperture i.e.
SIGN - CONVENTION
1. Whenever and where possible, rays of light are taken to travel from left to right.
2. Transverse distances are measured from optical centre and are taken to be positive while those below it negative.
3. Longitudinal distances are measured from optical centre and are taken to be positive if in the direction of light propagation and
negative if opposite to it e.g., according to our convention the sign of

While using the sign convention it must be kept in mind that -
(i) To calculate an unknown quantity the known quantities are substituted with sign in a given formula.
(ii) In the result, sign must be interpreted as there are number of sign conventions and same sign has different meaning in different conventions.
RULES FOR IMAGE FORMATION
In order to locate the image formed by a lens graphically following rules are adopted -
1. A ray passing through optical centre proceeds undeviated through the lens (by definition of optical centre).
2. A ray passing through first focus or directed towards it, after refraction from the lens becomes parallel to the principal axis (by definition of

3. A ray passing parallel to the principal axis after refraction through the lens passes or appear to pass through
4. Only two rays from the same point of an object are needed for image formation and the point where the rays after refraction through the lens intersect or appear to intersect is the image of the object. If they actually intersect each other the image is real and if they appear to intersect the image is said to be virtual.
CHECK POINT
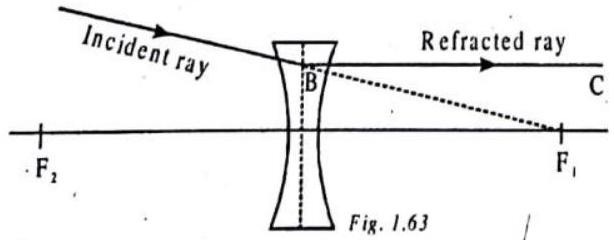
The diagram below shows the refracted ray

Show Answer
SOLUTION
Figure shows the refracted ray parallel to the principal axis. Therefore the incident ray must be travelling towards the first focus
CHECK POINT
The diagram shows an object

Show Answer
SOLUTION
To complete the diagram. The completed ray diagram is given below.

Since the image is inverted and magnified, the lens is convex.
IMAGE FORMATION BY A LENS
(a) For convergent or Convex Lens
| Position of object | Details of Image | Figure |
|---|---|---|
| At infinity | Real, inverted, diminished (m « 1), At F | |
| Between infinity and 2F | Real, inverted, diminished (m < 1), Between Fand 2F | |
| At 2F | Real, inverted, equal in size, (m-1) At 2F | |
| Between 2F and F | Real, inverted, enlarged |
|
| At F | Real, inverted, enlarged (m » 1), At infinity | |
| Between Focus & Pole | Virtual, erect, enlarged |
(b) For Divergent or Concave lens
If object is at infinity image will be formed at focus.
If object is, in front of lens, image will be virtual and erect.

LENS FORMULA
If an object is placed at a distance
Proof : Consider an object
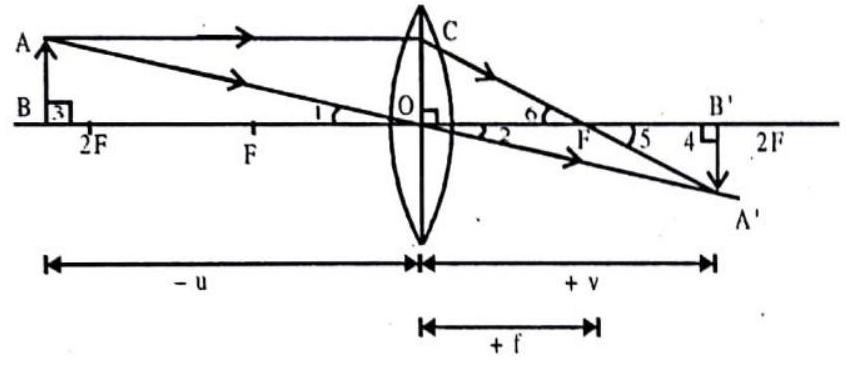
Fig. 1.67
(object distance)
(Image distance)
(Focal Length)
In
Therefore,
Now
In particular,
But
Since All distances are measured from optical centre, therefore,
Now comparing eq. (1) and (2),
Dividing both sides by
Similarly, we can prove the lens formula for a concave lens.
ILLUSTRATION-1.27
Two converging lenses with focal lengths
Show Answer
SOLUTION:
Find the image location for the first lens using the thin lens equation.
This image forms the object of the second lens located
The final image lies
ILLUSTRATION-1.28
A converging lens is used to read the small print in a contract. The lens is held
Show Answer
SOLUTION:
The fine print serves as the object for the lens
The thin lens equation gives
so
POWER OF A LENS
If focal length of a lens is measured in metre
The unit of power is diopter
CHECK POINT
Diving masks often have lenses built into the glass for divers who do not have perfect vision. This allows the individual to dive without the necessity for glasses, because the lenses in the faceplate perform the necessary refraction to provide clear vision. Normal glasses have lenses that are curved on both the front and rear surfaces. The lenses in a diving mask faceplate often only have curved surfaces on the inside of the glass. Why is this design desirable?
Show Answer
SOLUTION
The main reason for curving only the inner surface of the lenses in the diving mask faceplate is so that the diver can see clearly when looking at objects straight ahead while underwater and in the air. Consider light rays approaching the mask along a normal to the plane of the faceplate. If curved surfaces were on both the front and the back of the diving lens on the faceplate, refraction would occur at each surface. The lens could be designed so that these two refractions would give clear vision while the diver is in air. When the diver is underwater, however, the refraction between the water and the glass at the first interface is now different because the index of refraction of water is different from that of air. Thus, the vision would not be clear underwater. By making the outer surface of the lens flat, light is not refracted at normal incidence to the faceplate at the outer surface in either air or water-all of the refraction occurs at the inner glass-air surface. Thus, the same refractive correction exists in water and in air, and the diver can see clearly in both environments.
ILLUSTRATION-1.29
A convex lens of
Show Answer
SOLUTION:
(a) Power of convex lens
power of concave lens
(b) Power of combination
(c) Focal length of combination
(d) As power of combination is positive, therefore, combination behaves like a convex lens.
ILLUSTRATION-1.30
A doctor has prescribed a corrective lens of power +1.5 D. Find the focal length of the lens. Is the prescribed lens diverging or converging?
Show Answer
SOLUTION:
So the focal length is
Magnification produced by a lens.
If a thin object of linear size
Negative magnification implies that image is inverted with respect to object while positive magnification means that image is erect with respect to object.
Other formulae of magnification
For real extended object, if the image formed by a single lens in inverted (i.e.,
ILLUSTRATION-1.31
An object is placed at a distant of
Show Answer
SOLUTION:
The information given in the question ray diagram. It is given that
Let lens is placed at a distance of x from the object. Then
using m=
the focal length is 0.24 m(or 24cm)
ILLUSTRATION 1.32
A lens placed at a distance of 20 cm from an object produces a virtual image 2/3 the size of the object. Find the position of the image, kind of lens and its focal length.
Show Answer
SOLUTION:
Virtual image means, I is positive a and it t is given that I=
Further because u=-20 cm (given) using m=
we get
The f is negative thus the lens is a concave lens. Again using
we ger
the virtual image is on the same side of the object
LENS MAKER FORMULA
This formula gives a relation among the focal length
where,
If lens is placed in air, then
Sign convention for

In case of sun-goggles, the radii of curvature of two surfaces are equal with centre on same side i.e.,
ie.,
This is why sun-goggles have no power or infinite focal length. Same is true for a transparent sheet with the difference that here
COMBINATION OF LENSES
Case I: When two thin lenses are in contact.
In case of two thin lenses in contact if the first lens of focal length fi forms the image I₁ (of an object) at a distance v₁ from it
now the image
Adding above equations
i.e. the combination behaves as a single lens of equivalent focal length
Case II : When two thin lenses are separated by a certain distance.
If the two thin lens are separated by a distance
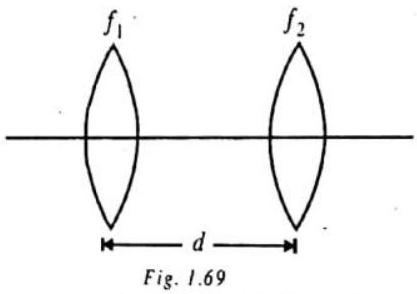
NOTE: (1) If two thin lenses of equal focal length but of opposite nature (i.e. one convergent and other divergent) are put in contact, the resultant focal length of the combination will be
(2) If two thin lens of same nature are put in contact then as
i.e. the resultant focal length will be lesser than smallest individual.
(3) If two thin lenses of opposite nature with different focal lengths are put in contact the resultant focal length will be of same nature as that of the lens of shorter focal length but its magnitude will be more than that of shorter focal length. If
each part has a focal length
i.e. each part have focal length

ILLUSTRATION-1.33
A convex lens of focal length
Show Answer
SOLUTION:
For combination of lenses
Therefore,
ILLUSTRATION-1.34
Ten identical converging thin lenses, each of focal length
Show Answer
SOLUTION:
For thin lenses in contact
SILVERING OF LENS
A lens has two surfaces. If one of the surfaces is silvered, the lens behaves as a mirror. The mechanism of the image formation can be understood in brief as given below.
Light from the object falls on the lens which produces a virtual image
Thus, on silvering the lens behaves as a mirror of focal length
where
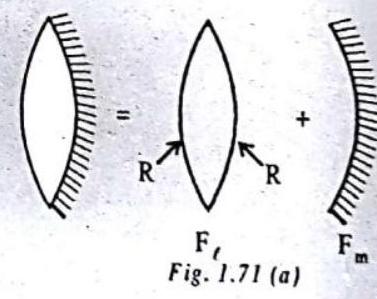
Case I: When a double convex lens is silvered.
Also, by lens maker formula,
Putting the values of
Case II : When a planes convex lens is silvered.
(i) If curved surface is silvered
In this case,
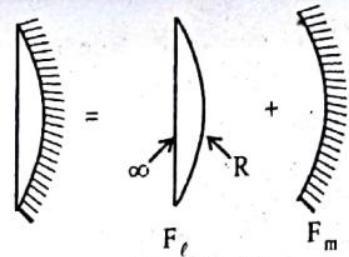
Fig. 1.71 (b)
(ii) If plane surface is silvered.
In this case,

ILLUSTRATION-1.35
The radius of curvature of a thin plano-convex lens is
Show Answer
SOLUTION:
(a) The silvered plano convex lens behaves as a concave mirror; whose focal length is given by
If plane surface is silvered

Here,
ILLUSTRATION-1.36
A luminous object is placed at a distance of
Show Answer
SOLUTION:
(c) For the lens,
Coincidence is possible when the image is formed at the centre of curvature of the mirror. Only then the rays refracting through the lens will fall normally on the convex mirror and retrace their path to form the image at
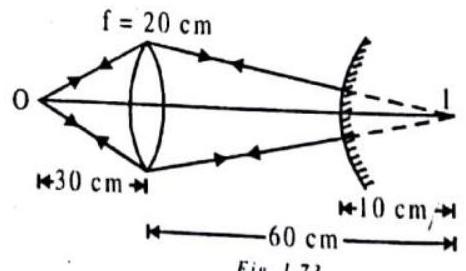
Fig. 1.73
CHROMATIC ABERRATION
The image of a white object (or illuminated by white light) formed by a lens is usually coloured and blurred, This defect of the image produced by a lens is called ‘chromatic aberration’. This defect arises because the refractive index of the material of the lens and lience the focal length of the lens, is different for different colors of light for a thin lens. Smaller the focal length of a lens (i,e, preater the power), smaller is the chromatic aberration in the lens.
SOME OTHER PROPERTIES OF LIGHT
As we know light shows dual nature - the nature of a particle in some cases and the nature of a wave in some other, When light behaves as a wave, it shows the following characteristics -
(i) Interference
(ii) Diffraction
(iii) Polarisation etc.
When light behaves as a particle, it performs phenomenon like photoelectric effect.
INTERFERENCE OF LIGHT
The colours in soap bubbles and oil slicks are due to this property of light. When two light waves of exactly same frequency travels in a medium, in the some direction simultaneously then due to their superposition, the intensity of light is maximum at some points while the intensity is minimum at some other points. This phenomenon is called interference of light. It is of two types:
(i) Constructive interference and
(ii) Destructive interference
When the waves meet a point with same phase, constructive interference is obtained at that point. Hence, at that point bright spot of light is seen.
But when the waves meet a point with opposite phase, destructive interference is obtained at that point. Hence, at that point dark spot of light is seen.
YOUNG’S DOUBLE SLIT EXPERIMENT
Fringes are produced by interference, which we discussed. Constructive and destructive interference is reviewed in fig. 1.74. We see that the addition, or superposition, of a pair of identical waves in phase with each other produces a wave of the same frequency but with twice the amplitude. If the waves are exactly one-half wavelength out of phase, their superposition results in complete cancellation. If they are out of phase by order nether amount narial cancellation occurs

In 1801, the wave nature of light was convincingly demonstrated when the British physicist and physician Thomas Young performed his now famous interference experiment. Young found that light directed through two closely spaced pinholes recombined to produce fringes of brightness and darkness on a screen behind. The bright fringes of light resulted from light waves

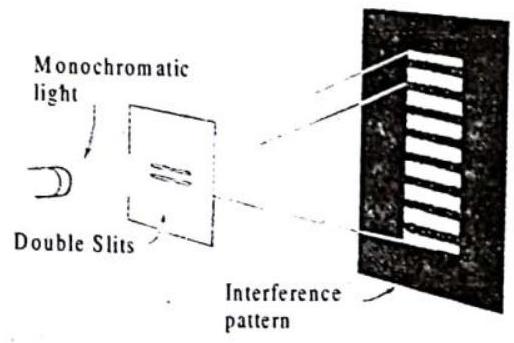
Fig.1.76: When monochromatic light passes through two closely spaced slits, a striped interference pattern is produced.
We see in figures and how the series of bright and dark lines results from the different path lengths from the slits to the screen. For the central bright fringe, the paths from each slit are the same length, and the waves arrive in phase and reinforce each other. The dark fringes on either side of the central fringe result from one path being longer (or shorter) by one-half a wavelength where the wave arrive half a wavelength where the wave arrive half a wavelength where the wave arrive half a wavelenght out of phase. The other sets of dark fringes occur where the paths differ by odd multiples of one-half wavelength :

Fig.I. 77 (a). Bright fringes occur when waves from both slits arrive in phase; dark areas result from the overlapping of waves that are out of phase.
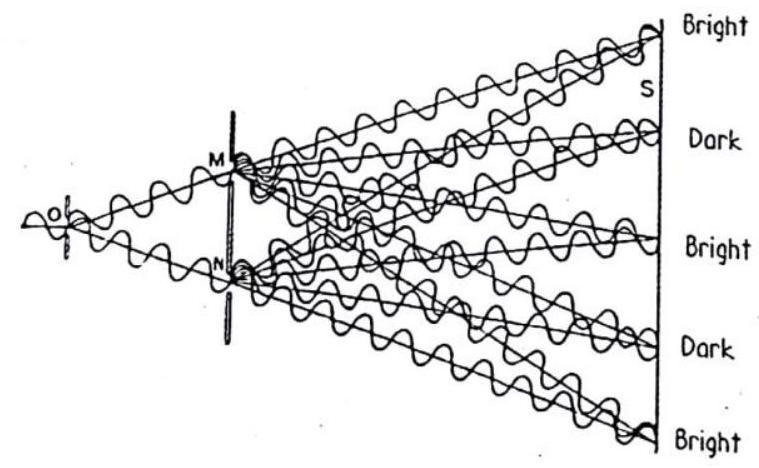
Fig.1.77(b) : Light from
CHECK POINT
If the double slits were illuminated with monochromatic red light, would the fringes be more widely or more closely spaced than if they were illuminated with monochromatic blue light? Why is it important that monochromatic (single-frequency) light be used ?
Show Answer
SOLUTION
They would be more widely spaced. Can you see in Fig.1.77 (b), that a slightly longer path- and therefore a slightly more displaced path- from the entrance slit to the screen would result for the longer waves of red light ? If light of various wavelengths were diffracted by the slits, dark fringes for one wavelength would be filled in with bright fringes for another, resulting in no distinct fringe pattern. If you haven’t seen this, be sure to ask your instructor to demonstrate it.
DIFFRACTION OF LIGHT
The wavelength of light is of the order of angstroms. So, when light waves encounter obstacles of very small sizes, the light waves 年 shadow of an object cannot be obtained on any screen placed behind it. Due to diffraction, light bends and travels into the region of geometrical shadow of the object and thus complete darkness is not found in the shadow. The brightness of light gradually decreases towards complete darkness as we go gradually into the geometrical shadow of the obstacle.
POLARISATION OF LIGHT
An ordinary source of light such as bulb consists of a large number of waves emitted by atoms or molecules in all directions symmetrically. Such light is called unpolarized light (Fig. 1.78 (a))

If we confine the direction of wave vibration of electric vector in one direction (with the help of polaroids or Nicol prism) perpendicular to the direction of wave propagation, then such type of light is called plane polarised or linearly polarised. The phenomenon by which, we restrict the vibrations of wave in a particular direction (fig.1.78 (b). Perpendicular to direction of wave propagation is called polarisation.
MISCELLANEOUS SOLVED EXAMLES
1. An object is situated at a distance of
Show Answer
Solution. For a spherical lens,
For convex lens,
2. An object of length
Show Answer
Solution. Given
3. A biconvex lens whose both the surfaces have same radii of curvature has a power of
Show Answer
Solution.
For an equiconvex lens
4. A lens placed at a distance of
Show Answer
Solution. Virtual image means,
Further because
we get,
The
we get
The virtual image is on the same side of the object.
5. Find the number of images formed by two mutually perpendicular mirrors.
Show Answer
Solution. Here,
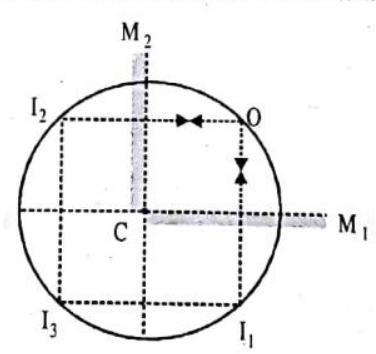
Thus, number of images formed
6. Two plane mirrors are inclined at an angle of

Show Answer
Solution.
The image of object
7. The focal length of a concave mirror is
Show Answer
Solution. Here image can be real or virtual. If the image is real
If the image is virtual
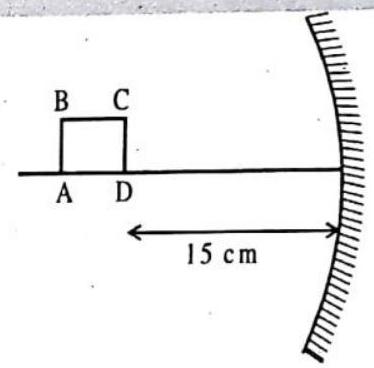
8. A square
Show Answer
Solution.
Now
9. A convex mirror has its radius of curvature
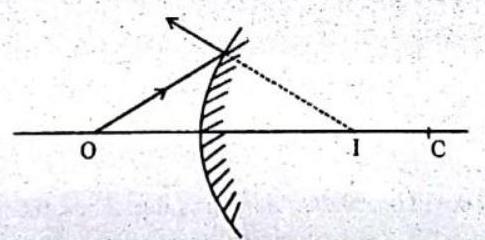
Show Answer
Solution. The situation is shown in figure.
Here
10. An object of length
Show Answer
Solution. The given situation is shown in figure. The focal length
or
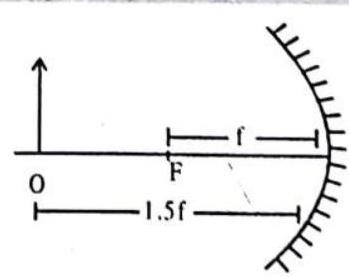
Now
or
The image is
11. Consider the situation shown in figure. Find maximum angle for which the light suffers total internal reflection at the vertical surface.
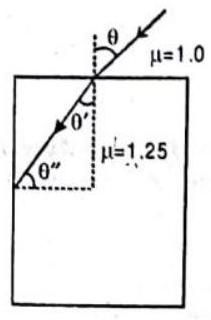
Show Answer
Solution. The critical angle for this case is
Since
From Snell’s law,
or
If
12. A converging lens has a focal length of
Show Answer
Solution.
or
13. Locate the image of the point

Show Answer
Solution. The net shift from one slab is
14. A lens has a power of +5 diopter in air. What will be its power if completely immersed in water? Given
Show Answer
Solution. Let
Using lensmaker’s formula
Dividing equation (ii) by equation (i), we get,
EXERCISE-1
Fill in the blank
DIRECTIONS : Complete the following statements with an appropriate word / term to be filled in the blank space(s).
1. The power of a convex lens is …………………… and that of a concave lens is ……………………
Show Answer
Answer: positive, negative.2. Light seems to travel in ……………………
Show Answer
Answer: straight lines.3. A light ray travelling obliquely from a denser medium to a rarer medium bends …………………… the normal. A light ray bends …………………… the normal when it travels obliquely from a rarer to a denser medium.
Show Answer
Answer: away from, towards4. In case of a rectangular glass slab, the refraction takes place at both …………………… interface and …………………… interface. The emergent ray is …………………… to the direction of incident ray.
Show Answer
Answer: air-glass, glass-air, parallel5. Power of a lens is the reciprocal of its. ……………………
Show Answer
Answer: focal length6. The SI unit of power of a lens is ……………………
Show Answer
Answer: dioptre7. The angle of incidence is . …………………… to the angle of reflection.
Show Answer
Answer: equal8. The reflecting surface of a spherical mirror may be curved
…………………… or ……………………
Show Answer
Answer: inwards, outwards.9. The surface of the spoon can be approximated to a …………………… mirror.
Show Answer
Answer: concave10. The centre of the reflecting surface of a spherical mirror is a point called the …………………… . a point called the …………….
Show Answer
Answer: pole11. The centre of curvature of a concave mirror lies in …………………… of it.
Show Answer
Answer: front12. Line passing through the pole and the centre of curvature of a spherical mirror is called the ……………………
Show Answer
Answer: principal axis13. A ray parallel to the principal axis, after reflection, will pass through the ……………………
Show Answer
Answer: principal focus14. The dentists use …………………… mirrors to see large images of the teeth of patients.
Show Answer
Answer: concave15. A transparent material bound by two surfaces, of which one or both sürfaces are spherical, forms a ……………………
Show Answer
Answer: lens.16. The degree of …………………… of light rays achieved by a lens is expressed in terms of its power.
Show Answer
Answer: convergence or divergence17. An object is placed in front of a spherical mirror. The image is found to be virtual for all positions of the object. The spherical mirror is ……………………
Show Answer
Answer: convex18. Two immiscible transparent liquids
Show Answer
Answer:True / False :
DIRECTIONS : Read the following statements and write your answer as true or false.
1. The reflecting surfaces, of all types, obey the laws of reflection.
Show Answer
Answer: True2. The magnification produced by a spherical mirror is the ratio of the height of the image to the height of the object.
Show Answer
Answer: True3. Light travels in vacuum with an enormous speed of
Show Answer
Answer: True4. The speed of light is different in different media.
Show Answer
Answer: True5. The refractive index of a transparent medium is the ratio of the speed of light in vacuum to that in the medium.
Show Answer
Answer: True6. The incident ray, the normal to the mirror at the point of incidence and the reflected ray, all lie in the same plane.
Show Answer
Answer: True7. Centre of curvature is not a part of the mirror.
Show Answer
Answer: True8. Image formed by a plane mirror is always virtual and erect.
Show Answer
Answer: False. Many books says plane mirror always form virtual image but plane mirror can form real image as shown.
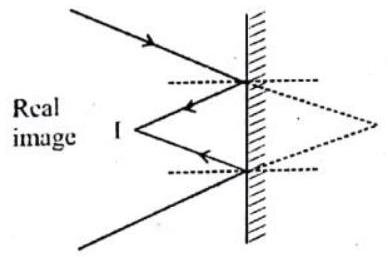
9. The principal focus of a spherical mirror lies midway between the pole and centre of curvature.
Show Answer
Answer: True10. Convex mirrors enable the driver to view much larger area than would be possible with a plane mirror.
Show Answer
Answer: True11. A concave lens will always give a virtual, erect and diminished image.
Show Answer
Answer: True12. A ray of light passing through the optical centre of a lens will emerge without any deviation.
Show Answer
Answer: True13. A plane mirror can form virtual images.
Show Answer
Answer: True14. An object is placed in front of a mirror and an image of it is formed at the object itself. The mirror mentioned in question is a convex mirror.
Show Answer
Answer: False15. A concave mirror can produce both real and virtual images.
Show Answer
Answer: True16. Light travels faster in glass than in air.
Show Answer
Answer: FalseMatch the following.
DIRECTIONS : Each question contains statements given in two columns which have to be matched. Statements
1. Match the following:
Show Answer
Answer:2. The graphs given apply to convex lens of focal length
| Column I | Column II |
|---|---|
| (A) |
 |
| (B) |
 |
| (C) |
 |
| (D) |
 |
Show Answer
Answer: (A)Very Short Answer Questions:
DIRECTIONS : Give answer in one word or one sentence.
1. If you want to see an enlarged image of your face, state whether you will use a concave mirror or a convex mirror?
Show Answer
Answer: Concave mirror2. In case of a spherical mirror, do both the sides act as reflecting surfaces?
Show Answer
Answer: No, only one side of the mirror acts as a reflecting surface and the other side is opaque.3. For driving a car, what type of mirror would you prefer to see the traffic at your back?
Show Answer
Answer: We prefer convex mirror for observing the traflic behind us because its field of view is much larger than the plane mirror. However, it gives erroneous idea about the speed of the vehicles behind us.4. A ray of light passes through the optical centre of a lens. Does it suffer any deviation?
Show Answer
Answer: A ray of light passing through the optical centre of a lens does not suffer any deviation.5. Will the focal length of the lens change when it is put in water?
Show Answer
Answer: Yes, the power of the lens will decrease or the focal length of the lens will increase when it is put in water.6. Define the principal focus of a concave mirror.
Show Answer
Answer: The point on the principal axis at which all the rays parallel and close to the principal axis meet after reflection from the concave mirror.7. What is a ray?
Show Answer
Answer: The path of light is called a ray.8. What is the radius of a plane mirror?
Show Answer
Answer: The radius of a plane mirror is infinity.9. Why does a convex mirror has a virtual principal focus ?
Show Answer
Answer: In a convex mirror, the reflected rays do not actually pass through the focus (F). So, a convex mirror has a virtual principal focus, which is situated behind the mirror.10. What is the nature of light?
Show Answer
Answer: Light is an electromagnetic wave which does not require a material medium for propagation.11. What is spherical mirror?
Show Answer
Answer: A spherical mirror is the mirror whose reflecting surface is a part of a hollow sphere.12. For what position of an object, a concave mirror forms a virtual and magnified image?
Show Answer
Answer: Between13. What type of mirror is formed when a mercury drop falls on the earth?
Show Answer
Answer: Convex mirror14. Define refraction.
Show Answer
Answer: The bending of light when it passes from one medium to another is called refraction.15. What is a rarer medium?
Show Answer
Answer: A medium, in which the speed of light is more, is known as optically rarer medium.16. What is a lens?
Show Answer
Answer: A lens is a piece of transparent glass bound by two surfaces out of which atleast one is curved.17. Define one dioptre.
Show Answer
Answer: One dioptre is the power of a lens whose focal length is Im18. Write down the magnification formula for a lens in terms of object distance and image distance. How does it differ from the corresponding formula for a mirror?
Show Answer
Answer: The linear magnification produced by a lens is equal to the ratio of image distance to the object distance.19. Differentiate between virtual image of a concave mirror and of a convex mirror.
Show Answer
Answer: The virtual image of a concave mirror is always magnified whereas the virtual image of a convex mirror is diminished.20. How does the frequency of a beam of ultra violet light change when it goes from air into glass?
Show Answer
Answer: Frequency remains same on change of medium.21. When light undergoes refraction at the surface of separation of two media, what happens to its wavelength?
Show Answer
Answer: Wavelength decreases on entering a denser medium and wavelength increases on entering a rarer medium.22. How does a focal length of convex lens change if monochromatic red light is used instead of monochromatic blue light?
Show Answer
Answer: Refractive index is more for blue light than red light. So the focal length is less for blue light.Short Answer Questions:
DIRECTIONS : Give answer in two to three sentences.
1. A person is in a room whose ceiling and two adjacent walls are mirrors. (a) How many images are formed? (b) How many images of himself can he see ? (c) Are all the images virtual and erect?
2. A high flying bird does not cast shadow on the ground. Why?
3. What is the difference between the images formed by a large and a small mirror?
4. For a plane mirror what is the focal length and the magnification?
5. The level of clear water in a clear colourless glass can be seen easily, but that of liquid helium cannot be. Why?
6. Why is convex mirror preferred as rear-view mirror in cars?
7. What do you mean by a normal to the reflecting surface?
Show Answer
Answer: A normal is the line drawn perpendicular to the reflecting surface at the point of incidence.8. What do you mean by a focal plane ?
Show Answer
Answer: A focal plane is an imaginary plane perpendicular to the principal axis and passes through the focus of the lens.9. A concave mirror produces three times magnified (enlarged) real image of an object placed at
Show Answer
Answer: Magnification,
Object distance,
Image distance,
We know that magnification for the mirror
10. Light enters from air to glass having refractive index 1.50 , What is the speed of light in the glass? The speed of light in vacuum is
Show Answer
Answer: Refractive index of glass
or
or Speed of light in glass
The speed of light in glass is
11. The refractive index of diamond is 2.42 . What is the meaning of this statement.
Show Answer
Answer: Diamond has a very high refractive index of 2.42. Larger the refractive index of a medium, greater is the bending of light when it enters the medium from air obliquely.12. Find the power of a concave lens of focal length
Show Answer
Answer: Focal length,
Power,
13. Find the focal length of a lens of power
Show Answer
Answer: The power of this lens has negative (-) sign, so it is a concave lens.
Power,
or
14. In what way is the word AMBULANCE printed infront of the hospital vans? Why is it printed this way?
Show Answer
Answer: The word AMBULANCE on the hospital vans is written in the form of its mirror image as because any vehicle, which is ahead of ambulance van, we can see the laterally inverted alphabets correctly from his rear-view mirror and make way for it to pass through and enable it to reach the hospital quickly.15. A convex lens is of focal length
Show Answer
Answer: Here, the focal length of the lens is given in
Now,
So, focal length,
Now,
We get,
Thus, power
The plus sign with the power indicates what it is a converging lens (or convex lens)
16. You read a newspaper because of the light that it reflects. Then why do you not see even a faint image of yourself in the newspaper?
17. The wall of a room is covered with a perfect plane mirror. Two movie films are made, one recording the movement of a man and the other of his image. From viewing the films later, can an outsider tell which is which?
18. Under what condition will a concave mirror produce an erect image? A virtual image ? An image smaller than the object? An image larger than the object?
Show Answer
Answer: The image will be virtual and erect if19. The image of an object formed by a lens on the screen is not in sharp focus. Suggest a method to get clear focussing of the image on the screen without disturbing the position of the object, the lens or the screen.
Show Answer
Answer: Put a block either to the rays of light coming along the edge or the middle of the lens.20. Refractive index of glass for light of yellow, green and red colours are
Show Answer
Answer:21. Give the ratio of velocities of light rays of wavelengths
Show Answer
Answer:22. An object is placed at a distance of
Show Answer
Answer: Given : Object distance
Magnification
We know that,
So, image is formed at a distance of
23. With respect to air, the refractive index of ice is 1.31 arid that of rock salt is 1.54 . Calculate the refractive index of rock salt with respect to ice.
Show Answer
Answer:24. Light enters from air into glass plate which has a refractive index of 1.50. Calculate the speed of light in glass. The speed of light in air is
Show Answer
Answer:
25. A concave mirror and a convex lens are held separately in water. What changes, if any, do you expect in the focal length of either?
Show Answer
Answer: Convex lens increases its focal length, while the focal length of concave mirror remains same.Long Answer Questions
DIRECTIONS : Give answer in four to five sentences.
1. Prove the mirror formula for reflection of light from a concave mirror.
2. An object
Show Answer
Answer: Radius of curvature of convex mirror,
Now
Using the mirror formula
Thus, image is formed at a distance of
3. A truck uses a convex mirror as view finder whose radius of curvature is
Show Answer
Answer: For convex mirror, we have given
So,
Using the mirror formula,
We get
or
Thus, the car would appear at
ror. We know that
Thus, size of the image of the car will be
4. An object is placed
Show Answer
Answer: Actual size of the car through the convex mirror.
According to cartesian sign convention,
We have the formula
Negative sign means that a real image is formed
5. Two thin converging lenses of focal lengths
Show Answer
Answer: 10D, 0.16. What is the focal length of a convex lens of focal length
Show Answer
Answer: 60 cm7. Two thin lenses of focal lengths
Show Answer
Answer: -10 cm,-10 D8. If the wavelength of incident light on a (i) concave mirror and (ii) convex lens is increased, how will the focal length of each of these change?
Show Answer
Answer: (i) Focal length of concave mirror remains same, since it is independent of the wavelength of light.
(ii) When wavelength is increased, refractive index of glass for the particular colour decreases. Since focal length depends on
9. Use the mirror formula to show that for an object lying between the pole and focus of a concave mirror, the image formed is always virtual in nature.
Show Answer
Answer: Mirror formula is,
Focal length and object distance are both
It is given
10. A concave lens has focal length of
Show Answer
Answer:
Using
Since
Image is enlarged and virtual.
(MCQ) Multiple Choice Questions
DIRECTIONS : This section contains multiple choice questions. Each question has 4 choices (a), (b), (c) and (d) out of which ONLY ONE is correct.
1. Where should an object be placed in front of a convex lens to get a real image of the size of the object?
(a) At the principal focus of the lens
(b) At twice the focal length
(c) At infinity
(d) Between the optical centre of the lens and its principal focus.
Show Answer
Answer: (b)2. A spherical mirror and a thin spherical lens have each a focal length of
(a) both concave.
(b) both convex.
(c) the mirror is concave and the lens is convex.
(d) the mirror is convex, but the lens is concave.
Show Answer
Answer: (a)3. Which of the following lenses would you prefer to use while reading small letters found in a dictionary?
(a) A convex lens of focal length
(b) A concave lens of focal length
(c) A convex lens of focal length
(d) A concave lens of focal length
Show Answer
Answer: (c)4. One light wave is incident upon a plate of refracting index
(a)
(b)
(c)
(d)
Show Answer
Answer: (d)5. An object is situated at a distance of
(a)
(c)
(b)
(d)
Show Answer
Answer: (d)6. An object is placed
(a) +2
(c) +0.5
(b) -2
(d) -0.5
Show Answer
Answer: (d)7. Two plane mirrors are set at right angle and a flower is placed in between the mirrors. The number of images of the flower which will be seen is
(a) One
(b) Two
(c) Three
(d) Four
Show Answer
Answer: (c)8. A man is
(a)
(b)
(c)
(d)
Show Answer
Answer: (a)9. An object is placed
(a) +2
(b) -2
(c) +0.5
(d) -0.5
Show Answer
Answer: (c)10. Light rays
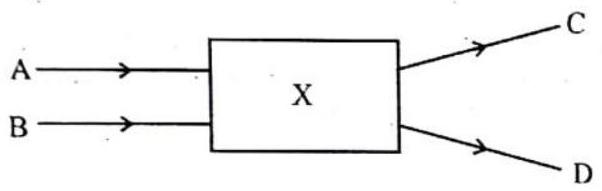
The optical component is a
(a) concave lens
(b) convex lens
(c) convex mirror
(d) prism
Show Answer
Answer: (a)11. An object is placed
(a) +5.0
(b) -5.0
(c) +0.20
(d) -0.20
Show Answer
Answer: (a)12. An object is placed at the radius of curvature of a concave spherical mirror. The image formed by the mirror is
(a) located at the focal point of the mirror.
(b) located between the focal point and the radius of curvature of the mirror.
(c) located at the center of curvature of the mirror.
(d) located out beyond the center of curvature of the mirror.
Show Answer
Answer: (c)13. If the refractive indices for water and diamond relative to air are 1.33 and 2.4 respectively, then the refractive index of diamond relative to water is -
(a) 55
(b) 1.80
(c) 3.19
(d) None of these
Show Answer
Answer: (b)14. There is an equiconvex lens of focal length of
(a)
(b)
(c)
(d)
Show Answer
Answer: (c)15. An object is placed
(a)
(b)
(c)
(d)
Show Answer
Answer: (b)16. When viewed vertically a fish appears to be 4 meter below the surface of the lake. If the index of refraction of water is 1.33, then the true depth of the fish is
(a) 5.32 metres
(b) 3.32 metres
(c) 4.32 metres
(d) 6.32 metres
Show Answer
Answer: (a)17. Light waves
(a) Require air or another gas to travel through
(b) Require an electric field to travel through
(c) Require a magnetic field to travel through
(d) Can travel through perfect vacuum
Show Answer
Answer: (d)18. An object is placed
(a)
(b)
(c)
(d)
Show Answer
Answer: (d)19. Morning sun is not so hot as the mid day sun because
(a) Sun is cooler in the morning
(b) Heat rays travel slowly is the morning
(c) It is God gift
(d) The sun’s rays travel a longer distance through atmosphere in the morning
Show Answer
Answer: (d)20. The layered lens shown below is made of two different transparent materials.
A point object is placed on its axis. The object will form
(a) one image
(b) infinite images
(c) no image
(d) two images
Show Answer
Answer: (d)21. An object is placed in front of a concave mirror of focal length
(a)
(b)
(c)
(d)
Show Answer
Answer: (d)22. A number of images of a candle flame can be seen in a thick mirror. The brightest image is
(a) Fourth
(b) Second
(c) Last
(d) First
Show Answer
Answer: (b)23. A ray from air enters water, then through a thick layer of glass placed below water. After passing through glass, it again comes out in air medium. Then final emergent ray will
(a) Bend towards the normal
(b) Bend away from the normal
(c) Suffer lateral displacement
(d) Have the same path as if it had not passed through glass and water.
Show Answer
Answer: (c)24. A concave spherical mirror has a radius of curvature of 100
(a)
(c)
(b)
(d)
Show Answer
Answer: (a)25. Light is incident on an air-water interface at an angle of
(a)
(b)
(c)
(d)
Show Answer
Answer: (a)26. Light reflected from a boundary between an unknown substance and air is seen to become
(a) 1.88
(c) 2.14
(b) 1.13
(d) 0.532
Show Answer
Answer: (a)27. An object is placed
(a)
(c)
(b)
(d)
Show Answer
Answer: (d)28. Under what conditions does a diverging lens form a virtual image of a real object
(a) Only if
(b) Only if
(c) Only if
(d) A diverging lens always forms a virtual image of a real object.
Show Answer
Answer: (d)29. A convex lens of focal length
(a)
(c) At infinity
(b)
(d)
Show Answer
Answer: (a)30. A lens produces a enlarged, virtual image. What kind of lens is it?
(a) converging
(b) diverging
(c) It could be either diverging or converging.
(d) None
Show Answer
Answer: (a)31. A camera lens focuses light from a
(a)
(b)
(c)
(d)
Show Answer
Answer: (a)32. In an experiment to determine the focal length of a concave lens, a student obtained the image of a distant window on the screen. To determine the focal length of the lens, she/he should measure the distance between the
(a) lens and the screen only
(b) lens and the window only
(c) screen and the window only
(d) screen and the lens and also between the screen and the window
Show Answer
Answer: (a)33. On the basis of experiment ’to trace the path of a ray of light passing through a rectangular glass slab’ four students ar. rived at the following interpretations :
I. Angle of incidence is greater than the angle of emergence.
II. Angle of emergence is less than the angle of refraction.
III. Emergent ray is parallel to the incident ray.
IV. Emergent ray is parallel to the refracted ray.
The correct interpretation is that of the student.
(a) I
(b) II
(c) III
(d) IV
Show Answer
Answer: (c)34. Light waves
(a) are mechanical waves
(b) are electromagnetic waves
(c) travel with the same velocity in all media
(d) requires a material medium for their propagation
Show Answer
Answer: (b)35. Virtual images of object of the same size are formed by
(a) a concave mirror
(b) a convex mirror
(c) a plane mirror
(d) all the above
Show Answer
Answer: (c)36. Two plane inclined mirrors form 5 images by multiple reflection. The angle of inclination is
(a)
(b)
(c)
(d)
Show Answer
Answer: (b)37. A bright
(a)
(b)
(c)
(d)
Show Answer
Answer: (c)38. The critical angle of a transparent medium denser than air
(a) increases with its refractive index
(b) decreases with its refractive index
(c) is independent of its refractive index
Show Answer
Answer: (b)39. Orange, blue and yellow are 3 of the colours formed by prism. Their order according to increasing deviation is
(a) blue, orange, yellow
(b) yellow, blue, orange
(c) blue, yellow, orange
(d) orange, yellow, blue
Show Answer
Answer: (d)40. Images formed by an object placed between two plane mirrors whose reflecting surfaces make an angle of
(a) Straight line a
(b) Zig-zag curve
(c) Circle
(d) Ellipse
Show Answer
Answer: (c)41. A diver in a swimming (d) Ellipse person lying on the pool wants to signal his distress to a proof torch
(a) He must direct the beat
(b) He must direct the beam of light vertically upwards
(c) He must direct beam horizontally which is slightly lesser than an angle to the vertical
(d) He must direct lhe ber than the critical angle which is slightly geater at an angle to the vertical which is slightly greater than the critical angle
Show Answer
Answer: (c)42. Two plane mirrors are inclined at an angle
(a)
(b)
(c) between
(d)
Show Answer
Answer: (b)43. In comparison to the case when a ray of light travels from glass to air, the critical angle for total internal reflection of light when a ray of light travels from glass to water is
(a) greater
(b) smaller
(c) same
(d) nothing can be predicted
Show Answer
Answer: (a)44. A glass slab is placed in the path of a beam of convergent light, then the point of convergence of light
(a) moves towards the glass slab
(b) moves away from the glass slab
(c) remains at the same point
(d) undergoes a lateral shift
Show Answer
Answer: (b)45. A real image is formed by a convex mirror when the object is placed at
(a) infinite
(b) between center of curvature and focus
(c) between focus and pole
(d) none of the above
Show Answer
Answer: (d)46. A virtual image is formed by a concave mirror when the object is placed between
(a) infinity and center of curvature
(b) center of curvature and focus
(c) focus and the pole
(d) All of the above
Show Answer
Answer: (c)47. Which of the following are used in a Kaleidoscope
(a) plane mirrors
(b) concave
(c) convex mirrors
(d) all of the above
Show Answer
Answer: (a)48. When a spherical convex lens made up of glass is immersed in water, its focal length
(a) decreases
(b) does not change
(c) increases
(d) none of the above
Show Answer
Answer: (c)49. Out of the following
(a) pole
(b) focus
(c) radius of curvature
(d) principal axis
for a spherical mirror, the quantities that do not depend on whether the rays are paraxial or not, are
(a) a, b, c and d
(b) only a, b and c
(c) only a, c and d
(d) only a and d
Show Answer
Answer: (c)50. A person standing at some distance from a mirror finds his image erect, virtual and of the same size. Then the mirror is possibly
(a) plane mirror
(b) concave mirror
(c) plane or concave mirror
(d) plane or concave or convex mirror
Show Answer
Answer: (d)More than One Correct:
DIRECTIONS : This section contains multiple choice questions. Each question has 4 choices (a), (b), (c) and (d) out of which ONE OR MORE may be correct.
1. Which of the following materials be used to make a lens?
(a) Water
(b) Glass
(c) Plastic
(d) Clay
Show Answer
Answer: ( a,b,c)2. The image formed by a concave mirror is observed to be virtual, erect and larger than the object. Where should not be the position of the object?
(a) Between the principal focus and the centre of curvature :
(b) At the centre of curvature
(c) Beyond the centre of curvature
(d) Between the pole of the mirror and its principal focus.
Show Answer
Answer: (a,b,c)3. No matter how far you stand from a mirror, your image appears erect. The mirror may be
(a) plane
(b) concave
(c) convex
(d) none of these
Show Answer
Answer: (a,c)4. A lens behaves as a converging lens in air and diverging lens in water. The refractive index of the material of the lens can’t be
(a) 1
(b) between 1 and 1.33
(c) 1.33
(d) greater than 1.33
Show Answer
Answer: (a,c,d)5. On passing through a glass slab, red light doesn’t suffer a change of
(a) wavelength
(b) frequency
(c) amplitude
(d) velocity
Show Answer
Answer: (b,c)6. The focal length of a concave mirror doesn’t depend upon
(a) The radius of curvature of the mirror
(b) The object distance from the mirror
(c) The image distance from the mirror
(d) The material of mirror
Show Answer
Answer: (b,c)7. The radius of curvature of a plane mirror can’t be
(a) zero
(b) infinite
(c) negative
(d) finite
Show Answer
Answer: (a,c,d)8. Tick out the correct statements in the following
(a) Light travels with a speed greater than that of sound
(b) Light cannot travel through vacuum
(c) Light travels in a straight line
(d) Light has no weight
Show Answer
Answer: (a,c,d)9. Choose the wrong statements regarding the image formation in a convex spherical mirror
(a) Images are always larger than the actual object
(b) Images are always smaller than the actual object
(c) Images are always of the same size as the actual object
(d) Images are always half of the actual object
Show Answer
Answer: (a,c,d)10. The image formed by a convex spherical mirror is
(a) virtual
(b) erect
(c) real
(d) inverted
Show Answer
Answer: (a,b)11. When light passes from air into glass it experiences a change of
(a) Speed
(c) Frequency
(b) Wavelength and speed
(d) amplitude
Show Answer
Answer: (a,b)12. If a real object is placed inside the focal point of a concave mirror, the image is
(a) upright
(b) real
(c) virtual
(d) inverted
Show Answer
Answer: (a,c)13. A person standing infront of a mirror finds his image smaller than himself and erect. This implies the mirror must not be
(a) plane
(b) concave
(c) convex
(d) None of the above
Show Answer
Answer: (a,b,d)14. Choose the wrong statements regarding refraction of light
(a) The bending of light rays when they enter from one medium to another medium
(b) Splitting of white light into seven colours when it passes through the prism
(c) Bending of light round corners of obstacles and apertures
(d) Coming back of light from a bright smooth surface
Show Answer
Answer: (b,c,d)15. A converging lens has a focal length of
(a) upright
(b) inverted
(c) virtual
(d) enlarged
Show Answer
Answer: (a,c,d)16. Four students reported the following observation tables for the experiment, to trace the path of a ray of light passing through a glass slab for different angles of incidence. The observations, likely to be wrong are those of student.
I
II
III
(a) I
(b) II
(c) III
(d)
Show Answer
Answer: (a,c,d)17. The absolute refractive index of a medium depends on
(a) nature of the medium only
(b) wavelength of light only
(c) temperature of the medium only
(d) the angle of incidence
Show Answer
Answer: (a,b,c,d)18. Mark the correct statements
(a) Refractive indey decreases with increase in temperature
(b) Refractive index depends on the angle of incidence
(c) Foucault demonstrated experimentally that the speed of light in air is more than that in water
(d) Polarization of light was discovered by Malus
Show Answer
Answer: (a,c,d)19. Mark the correct statements about a virtual image
(a) A virtual image can be photographed
(b) A virtual image can be seen
(c) A virtual image can be photographed by exposing a film at the location of the image
(d) A virtual image may be diminished or enlarged in size in comparison to an object.
Show Answer
Answer: (a,b,d)20. Mark the correct statements
(a) A convex mirror produces an erect image
(b) A convex mirror always produces an erect image of an erect object
(c) A convex mirror always produces a diminished in size image
(d) A convex mirror is used as a shaving mirror
Show Answer
Answer: (a,b,c)21. In vacuum the speed of light does not depend on
(a) Wavelength
(b) Frequency
(c) Intensity
(d) Speed of observer
Show Answer
Answer: (a,b,c)22. When light passes from air to water which of the following changes
(a) Wavelength
(b) Velocity
(c) Frequency
(d) Colour
Show Answer
Answer: (a,b)23. In case of reflection by a plane-mirror, which of the following statements are not correct
(a) It can never give real image
(b) It can never give inverted image
(c) It changes left into right
(d) It changes front into back
Show Answer
Answer: (a,b,c)24. If two mirrors are inclined to each other at
(a) One
(b) Two
(c) Three
(d) Four
Show Answer
Answer: (a,b)25. In case of three plane-mirrors meeting at a point to form a corner of a cube, if incident light suffers one reflection on each mirror
(a) The emergent ray is antiparallel to incident one
(b) The emergent ray is perpendicular to incident one
(c) The emergent ray is in phase with incident one
(d) The emergent ray is in opposite phase with incident one
Show Answer
Answer: (a,d)26. A plane mirror, reflecting a ray of incident light, is rotated through an angle
(a) the reflected ray does not rotate
(b) the reflected ray rotates an angle 0
(c) the reflected ray rotates an angle
(d) the incident ray is fixed
Show Answer
Answer: (c,d)27. Five images are formed, if two plane-mirrors are inclined to cach other at an angle of
(a) 6
(c)
(b)
(d) 9
Show Answer
Answer: (a,b,c)28. Out of the following which statements are correct?
(a) Two plane mirrors are inclined to each other at an angle of
(b) A bird flying high up in the air does not cast a shadow on the ground because layers of atmosphere are dense.
(c) If a ray reflected successively from two plane mirrors inclined at a certain angle undergoes a deviation of
(d) A clock indicates a time of 3.25 . On seeing it in a plane mirror, the time appears as 8.35 .
Show Answer
Answer: (a,c,d)Fill In The Passage :
DIRECTIONS : Fill in the blanks in the following passage(s) from the words given inside the box.
I.
When a ray of light passes from denser to rarer medium, the refracted ray bends ………1………. from the normal. Hence the angle of refraction is ………2……….. the angle of incidence. Gradually if the angle of incidence increases, angle of refraction also increases. At a particular angle of incidence, the refracted ray just grazes the refracting surface or the angle of refraction is equal to ……….3……… . This angle of incidence in the denser medium is called ……….4………. If the angle of incidence is further increased the rays do not undergo refraction, it gets ………5………. into the same optically denser medium. This is known as ……..6………….
Show Answer
Answer:
-
away
-
greater than
-
-
critical angle
-
reflected
-
total internal reflection
II.
A lens is a transparent material which is bounded by ………1………. spherical surfaces or one spherical surface and one plane surface. Lens are of two types, namely ……….2……… and ……..3………… A convex lens has one or two spherical surfaces, such that it is ……………….4……………. at the centre than at the edges. A concave lens has one or two spherical surfaces, such that it is ………5……….. at the centre than at its edge.
Show Answer
Answer:
-
Two
-
convex lens
-
concave lens
-
thicker
-
thinner
III.
Cartesian sign convention is used now-a-days. According to this convention, all distances are measured from ………..1……… Distances measured in the direction of incident light is taken as ……….2……………. and distance measured against incident light is taken as ……………3….. . According to sign convention, ………..4……… of a couvex lens is positive and that of the …….5…………. is negative.
Show Answer
Answer:
1. optical centre
2. positive
3. negative
4. focal length
5. concave lens
Passage Based Questions:
DIRECTIONS : Study the given passage(s) and answer the following questions.
Passage-I
Inside a substance such as glass or water, light travels more slowly than it does in a vacuum. If
Table : Indices of refraction of Custon glass
| Approximately colour | Wavelength in vacuum (nm) | Indices |
|---|---|---|
| yellow | 580 | 1.5 |
| yellow orange | 600 | 1.498 |
| orange | 620 | 1.496 |
| orange red | 640 | .1 .494 |
1. Inside Custon glass
(a) Orange light travels faster than yellow light
(b) Yellow light travels faster than orange light
(c) Orange and Yellow light travels equally fast
(d) We cannot determine which color of light travels faster
Show Answer
Answer: (a)2. For blue-green of wavelength
(a) 1.49
(b) 1.50
(c) 1.51
(d) 1.52
Show Answer
Answer: (c)3. Which of the following phenomena happens because
(a) A lens focuses light
(b) A prism breaks sunlight into different colors
(c) Total internal reflections ensures that light travels down a fiber optic cable
(d) Light rays entering a pond change direction at the pond’s surface
Show Answer
Answer: (b)Passage-II
A convex lens of focal length
1. The power of the convex lens is
(a)
(b)
(c)
(d)
Show Answer
Answer: (a) Power of convex lens2. The power of the concave lens is
(a) +5D
(b)
(c)
(d)
Show Answer
Answer: (c) Power of concave lens3. The focal length of the combination of lenses is
(a)
(b)
(c)
(d)
Show Answer
Answer: (b) Power of combination
Passage-III
A
1. What is the distance of image from the pole of lens?
(a)
(b)
(c)
(d)
Show Answer
Answer: Object size
Since,
(a)
Then
Positive sign of
Therefore image is real and inverted.
2. The size of the image formed by the lens is
(a) 1 twice the object size
(b) halved the object size
(c) one-fourth the object size
(d) one -third the object size
Show Answer
Answer:
So, size of image is twice the size of object.
3. What is the power of the used lens?
(a)
(b)
(c)
(d)
Show Answer
Answer: (a) PowerAssertian & Reason:
DIRECTIONS : Each of these questions contains an Assertion followed by Reason. Read them carefully and answer the question on the basis of following options. You have to select the one that best describes the two statements.
(a) If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
(b) If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
(c) If Assertion is correct but Reason is incorrect.
(d) If Assertion is incorrect but Reason is correct.
1. Assertion : A point object is placed at a distance of
Reason : For above given system the equation
Show Answer
Answer: (c)2. Assertion : When a concave mirror is held under water, its focal length will increase.
Reason : The focal length of a concave mirror is independent of the medium in which it is placed.
Show Answer
Answer: (d)3. Assertion : A convex mirror is used as a driver’s mirror.
Reason : Because convex mirror’s field of view is large and images formed are virtual, erect and diminshed.
Show Answer
Answer: (a)4. Assertion : In visible light
Reason: This follows from Cauchy’s formula
Show Answer
Answer: (a)5. Assertion : Keeping a point object fixed, if a plane mirror is moved, the image will also move.
Reason : In case of a plane mirror, distance of object and Its image is equal from any point on the mirror.
Show Answer
Answer: (d)6. Assertion : When the object moves with a velocity
Reason : The minimum height of the mirror to be required to see the full image of man of height
Show Answer
Answer: (b)7. Assertion : If both plane mirror and object are moved through a distance
Reason : When the object is fixed and plane mirror is moved through a distance
Show Answer
Answer: (c)8. Assertion : As the temperature of a medium increases the refractive index decreases.
Reason : When a ray travels from vacuum to a medium, then
Show Answer
Answer: (b)9. Assertion : If a spherical mirror is dipped in water, its focal length remains unchanged.
Reason : A laser light is focused by a converging lens. There will be a significant chromatic aberration.
Show Answer
Answer: (c)10. Assertion : A virtual image cannot be photographed.
Reason : Only real objects are photographed.
Show Answer
Answer: (c) An image is a plane mirror is virtual and it can be photographed.11. Assertion : The small object, to be seen in a microscope, is kept within the two foci of its objective.
Reason : In this case, the image formed by the objective is nearer to the eyepiece.
Show Answer
Answer: (c) Object is placed between12. Assertion : A point source of light is placed at a distance of
Reason: In chromatic aberration the rays of different colours fail to converge at a point after going through a converging lens.
Show Answer
Answer: (b)13. Assertion : Light rays retrace their path when their direction is reversed (Law of reversibility of light rays)
Reason : For the refraction light, water is denser than air, but for the refraction of sound, water is rarer than air.
Show Answer
Answer: (b)14. Assertion : If the angle between the two plane mirror is
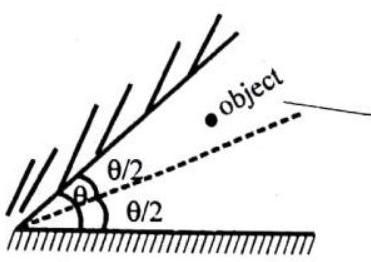
Reason : For given system of mirror the total number of images formed due to successive reflection is equal to either
Show Answer
Answer: (a)15. Assertion : Red light travels faster in glass than green light.
Reason : The refractive index of glass is less for red light than for green light.
Show Answer
Answer: (a)16. Assertion : Speed of light in glass of
Reason : According to dual theory, light has particle nature and wave nature simultaneously.
Show Answer
Answer: (c)17. Assertion : As light travels from one medium to another, the frequency of light does not change.
Reason : Because frequency is the characteristic of source.
Show Answer
Answer: (a)Muliple Matching Questions
DIRECTIONS : Each question has four statements
1. A convex lens
Show Answer
Answer: (A)2. In the followoing columns, the positon of an object is given is column
Show Answer
Answer: (A)HOTS Subjective Questions:
DIRECTIONS : Answer the following questions.
1. A truck uses a convex mirror as view finder whose radius of curvature is
Show Answer
Answer: For convex mirror, we have given
So,
Using the mirror formula.
We get
or
Thus, the car would appear at
We know that
Thus, size of the image ois car will be
2. An object is placed at a distance of
Show Answer
Answer:
The mirror formula is,
Substituting the values of
have
3. A monochromatic ray of light strikes the surface of a transparent medium at an angle of incidence
Show Answer
Answer: Here, sine of angle of incidence
Now, we have
Hence, the refractive index of the medium is 1.22 .
4. An object
Show Answer
Answer: Since lens is convex, therefore
Given
Since formula for a lens is
Since ’
Since
Thus the image is
5. A real image,
Show Answer
Answer: Since the image is real and diminshed, the lens must be convex and the object must be placed beyond
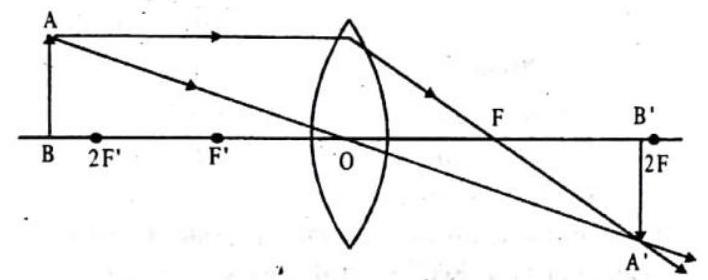
Given :
We have,
Now focal length is given by :
6. A concave lens has focal length of
Show Answer
Answer: A concave lens always forms a virtual, erect image on the same side of the object.
Image distance
Focal length
Object distance
Thus, the object distance is
Magnification,
7. A man standing in front of a spherical mirror, finds his image having a very small head, a fat body and legs of normal size. What types of mirrors are used in the small parts?
Show Answer
Answer: A very small head
A fat body
Legs of normal size
8. A glass block
Show Answer
Answer:
9. A postage stamp placed under a glass, appears raised by
Show Answer
Answer: Let real thickness of glass
We know
10. A
Show Answer
Answer: Let the scale be
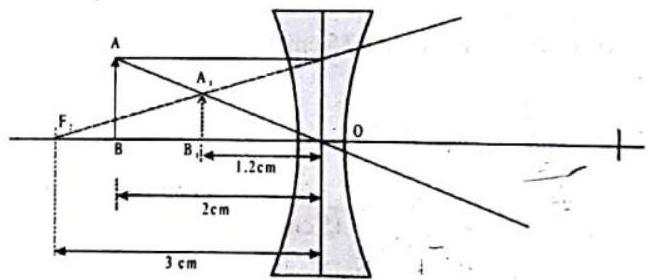
On constructing the ray diagram, it is found
Distance of the image from lens
Nature : Image is virtual, erect and diminished.
11. An image
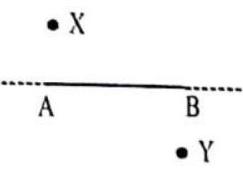
12. A concave spherical mirror has a radius of curvature of
Show Answer
Answer:
(a) real inverted reduced
(b) real, inverted, same size
(c) no image is formed
(d) virtual, erect, enlarged
13. In previous question instead of concave if convex mirror (same radius of curvature) is used what will be the answer
Show Answer
Answer:
(a) virtual, erect, reduced
(b) virtual, erect, reduced
(c) virtual, erect, reduced
(d) virtual, erect, reduced
14. A beam of light converges to a point
(b) a concave lens of focal length
Show Answer
Answer: (a)15. (a) Determine the ’effective focal length’ of the combination of a convex lens of focal length
(b) An object
Show Answer
Answer: (a) (i)16. An object
Show Answer
Answer:
Using
With sign convention,
Using
17. An object
Show Answer
Answer:
Using
18. An object
Show Answer
Answer:
Using
Using
19. An object
(i) distance at which the object is placed and
(ii) size and nature of the image formed.
Show Answer
Answer: Here
(ii)
From (i) and (ii), it is clear that image is formed on the same side of object placed at a distance of
20. An object
Show Answer
Answer: For a concave mirror
Given :
From mirror equation, we know that
Also
Position of image is
Nature of image : Real, inverted, same size (
21. A convex lens has a focal length of
Show Answer
Answer: Focal length of convex lens,
From lens formula
Negative sign shows that image is real.
22. A convex lens has a focal length of
Show Answer
Answer: Given : For convex lens
From lens formula
So, the object should be placed at a distance of
Magnification produced by lens,
Hence, real, inverted and same size image is obtained.
23. An object
Show Answer
Answer: For a concave mirror,
From mirror equation
i.e., image is formed behind the mirror at a distance of
Also, magnification
So, image is erect and twice the size of object.
24. An object
Show Answer
Answer: Given :
Also,
Therefore, Position of image :
Size of image : enlarge
25. Find the position, nature and size of the image of an object
Show Answer
Answer:
Mirror formula:
Position : image is formed behind the mirror at a distance of
Nature : virtual, erect, enlarged Size of image : Twice the size of object.
26. Where should an object be placed from a converging lens of focal length
Show Answer
Answer:
Using,
we get,
27. Find the position of the object which when placed in front of a convex mirror produces a virtual image, which is half the size of the object.
Show Answer
Answer: Convex mirror,
Image is virtual,
Therefore from
Object has to be at a distance equal to focal length.
28. Find the position of an object which when placed in front of a concave mirror of focal length
Show Answer
Answer:
Using
we get
29. An object is kept in front of a concave mirror of focal length
Show Answer
Answer:
For Real Image,
using
For Virtual Image,
using
we get,
The two possible positions are
30. Monochromatic light of wavelength
Show Answer
Answer:
Refractive index of water
(a) Reflected light will have same wavelength, frequency and velocity.
70 Lb) The frequency is sament
(b) The frequency is same with refracted light. But, velocity and wavelength vary.
Since,
velocity in water
Since,
wavelength in water is
31. An object
Show Answer
Answer:
using
Image formed is real and is at a distance of
Image is inverted since
32. (a) State the relation between object distance, image distance and focal length of a spherical mirror.
(b) A concave mirror of focal length
(c) Draw a ray diagram to show the image formed by a concave mirror when an object is placed between pole and focus of the mirror.
Show Answer
Answer: (a) The relation between object distance, image distance and focal length of a spherical mirror is given by
where
From mirror equation
Also, Magnification,
Hence, the image is formed at a distance of
Nature of image : Virtual, erect.
Size of image : Magnified, i.e., thrice the size of object.
(c) Position of object : Between pole and focus Mirror: Concave.
Position of image : Behind the mirror.
Nature of image : Virtual, enlarged and erect.