अध्याय 07 त्रिभुज
7.1 भूमिका
आप पिछली कक्षाओं में, त्रिभुजों और उनके विभिन्न गुणों के बारे में अध्ययन कर चुके हैं। आप जानते हैं कि तीन प्रतिच्छेदी रेखाओं द्वारा बनाई गई एक बंद आकृति (closed figure) एक त्रिभुज (triangle) कहलाती है (‘त्रि’ का अर्थ है ‘तीन’)। एक त्रिभुज की तीन भुजाएँ, तीन कोण और तीन शीर्ष होते हैं। उदाहरणार्थ, आकृति 7.1 में दिए त्रिभुज
7.2 त्रिभुजों की सर्वांगसमता

आकृति 7.1
आपने यह अवश्य ही देखा होगा कि आपकी फोटो की एक ही साइज की दो प्रतियाँ सर्वसम (identical) होती हैं। इसी प्रकार, एक ही माप की दो चूड़ियाँ और एक ही बैंक द्वारा जारी किए गए दो एटीएम (ATM) कार्ड सर्वसम होते हैं। आपने देखा होगा कि यदि एक ही वर्ष में ढले (बने) दो एक रुपए के सिक्कों में से एक को दूसरे पर रखें, तो वे एक दूसरे को पूर्णतया ढक लेते हैं।
क्या आपको याद है कि ऐसी आकृतियों को कैसी आकृतियाँ कहते हैं? निःसंदेह ये सर्वांगसम आकृतियाँ (congruent figures) कहलाती हैं (‘सर्वांगसम’ का अर्थ है ‘सभी प्रकार से बराबर’, अर्थात् वे आकृतियाँ जिनके समान आकार और समान माप हैं)।
अब एक ही त्रिज्या के दो वृत्त खींचिए और एक को दूसरे पर रखिए। आप क्या देखते हैं? ये एक दूसरे को पूर्णतया ढक लेते हैं और हम इन्हें सर्वांगसम वृत्त कहते हैं।
इसी क्रियाकलाप की एक ही माप की भुजाओं वाले दो वर्गों को खींच कर और फिर एक वर्ग को दूसरे वर्ग पर रखकर (देखिए आकृति 7.2) अथवा बराबर भुजाओं वाले दो समबाहु त्रिभुजों को एक दूसरे पर रखकर, पुनरावृत्ति कीजिए। आप देखेंगे कि वर्ग सर्वांगसम हैं और समबाहु त्रिभुज भी सर्वांगसम हैं।

आकृति 7.2
आप सोच सकते हैं कि हम सर्वांगसमता का अध्ययन क्यों कर रहे हैं। आपने अपने रेफ्रीजरेटर में बर्फ की ट्रे (ice tray) अवश्य ही देखी होगी। ध्यान दीजिए कि बर्फ जमाने के लिए बने सभी खाँचे सर्वांगसम हैं। ट्रे में (खाँचों के लिए प्रयोग किए गए साँचों की गहराइयाँ भी सर्वांगसम होती हैं (ये सभी आयताकार या सभी वृत्ताकार या सभी त्रिभुजाकार हो सकते हैं)। अतः, जब भी सर्वसम (एक जैसी) वस्तुएँ बनानी होती हैं, तो साँचे बनाने के लिए सर्वांगसमता की संकल्पना का प्रयोग किया जाता है।
कभी-कभी आपको अपने पेन के रिफिल (refill) बदलने में भी कठिनाई हो सकती है, यदि नया रिफिल आपके पेन के साइज का न हो। स्पष्टतः रिफिल तभी पेन में लग पाएगा, जबकि पुरानी रिफिल और नया रिफिल सर्वांगसम होंगे।
इस प्रकार, आप दैनिक जीवन की स्थितियों में ऐसे अनेक उदाहरण ज्ञात कर सकते हैं, जहाँ वस्तुओं की सर्वांगसमता का उपयोग होता है।
क्या आप सर्वांगसम आकृतियों के कुछ और उदाहरण सोच सकते हैं?
अब, निम्न में से कौन-कौन सी आकृतियाँ आकृति 7.3 (i) में दिए वर्ग के सर्वांगसम नहीं हैं?

आकृति 7.3
(ii) और आकृति 7.3 (iii) में दिए बड़े वर्ग स्पष्टतः आकृति 7.3 (i) के वर्ग के सर्वांगसम नहीं हैं। परन्तु आकृति 7.3 (iv) में दिया हुआ वर्ग आकृति 7.3 (i) में दिए वर्ग के सर्वांगसम है।
आइए अब दो त्रिभुजों की सर्वांगसमता की चर्चा करें।
आप पहले से यह जानते हैं कि दो त्रिभुज सर्वांगसम होते हैं, यदि एक त्रिभुज की भुजाएँ और कोण दूसरे त्रिभुज की संगत भुजाओं और कोणों के बराबर हों।
अब, निम्न में से कौन-कौन से त्रिभुज आकृति 7.4 (i) में दिए त्रिभुज

आकृति 7.4
आकृति 7.4 (ii) से आकृति 7.4 (v) तक के प्रत्येक त्रिभुज को काट कर उसे पलट कर
यदि
ध्यान दीजिए कि जब
अर्थात् भुजा
ध्यान दीजिए कि इस संगतता के अंतर्गत,
इसी प्रकार, आकृति 7.4 (iii) के लिए,
तथा
आकृति 7.4 (iv) के त्रिभुज और
अतः, त्रिभुजों की सर्वांगसमता को सांकेतिक रूप में लिखने के लिए, उनके शीर्षों की संगतता को सही प्रकार से लिखना आवश्यक है।
ध्यान दीजिए कि सर्वांगसम त्रिभुजों में संगत भाग बराबर होते हैं और ‘सर्वांगसम त्रिभुजों के संगत भागों के लिए’ हम संक्षेप में ’
7.3 त्रिभुजों की सर्वांगसमता के लिए कसौटियाँ
पिछली कक्षाओं में, आप त्रिभुजों की सर्वांगसमता के लिए चार कसौटियाँ (criteria) या नियम (rules) पढ़ चुके हैं। आइए इनका पुनर्विलोकन करें।
एक भुजा

आकृति 7.5
अब दो त्रिभुज खींचिए जिनमें एक भुजा

आकृति 7.6
देखिए कि ये दोनों त्रिभुज सर्वांगसम नहीं हैं।
इस क्रियाकलाप को त्रिभुजों के कुछ और युग्म खींच कर दोहराइए।
अतः, भुजाओं के एक युग्म की समता अथवा भुजाओं के एक युग्म और कोणों के एक युग्म की समता हमें सर्वांगसम त्रिभुज देने के लिए पर्याप्त नहीं है।
उस स्थिति में क्या होगा जब बराबर कोणों की भुजाओं का अन्य युग्म भी बराबर हो जाए?
आकृति 7.7 में
पिछली कक्षाओं से याद कीजिए कि इस स्थिति में, दोनों त्रिभुज सर्वांगसम होते हैं। आप इसका सत्यापन,

आकृति 7.7
यह त्रिभुजों की सर्वांगसमता की पहली कसौटी (criterion) है।
अभिगृहीत 7.1 (SAS सर्वांगसमता नियम): दो त्रिभुज सर्वांगसम होते हैं, यदि एक त्रिभुज की दो भुजाएँ और उनका अंतर्गत कोण दूसरे त्रिभुज की दो भुजाओं और उनके अंतर्गत कोण के बराबर हों।
इस परिणाम को इससे पहले ज्ञात परिणामों की सहायता से सिद्ध नहीं किया जा सकता है और इसीलिए इसे एक अभिगृहीत के रूप में सत्य मान लिया गया है (देखिए परिशिष्ट 1)।
आइए अब कुछ उदाहरण लें।
उदाहरण 1 : आकृति 7.8 में
(i)
(ii)
हल : (i)

आकृति 7.8
साथ ही, क्योंकि
इसलिए,
(ii) सर्वांगसम त्रिभुजों
अतः,
उदाहरण 2 :
हल :
अतः,
इसलिए,

आकृति 7.9
आइए अब दो त्रिभुजों की रचना करें जिनकी दो भुजाएँ 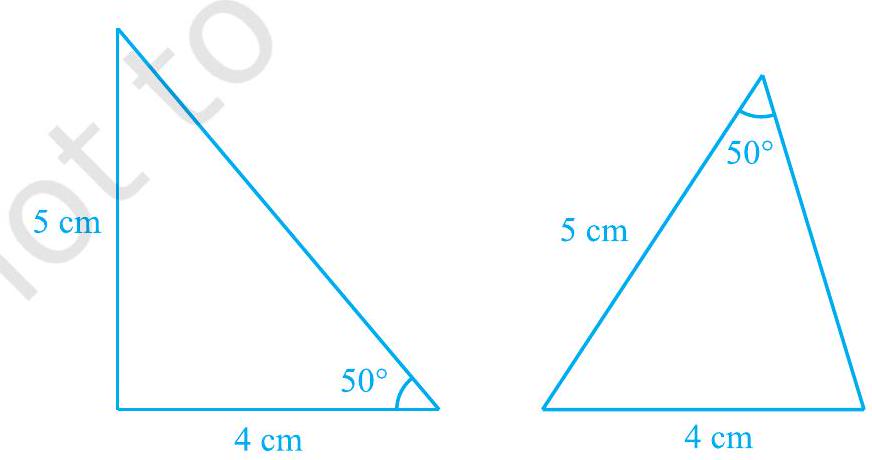
आकृति 7.10
ध्यान दीजिए कि ये दोनों त्रिभुज सर्वांगसम नहीं हैं।
त्रिभुजों के कुछ अन्य युग्म लेकर इस क्रियाकलाप को दोहराइए। आप देखेंगे कि दोनों त्रिभुजों की सर्वांगसमता के लिए यह आवश्यक है कि बराबर कोण बराबर भुजाओं के अंतर्गत कोण हो।
अतः, SAS नियम तो सत्य है, परन्तु ASS या SSA नियम सत्य नहीं है।
अब, ऐसे दो त्रिभुजों की रचना करने का प्रयत्न करिए, जिनमें दो कोण 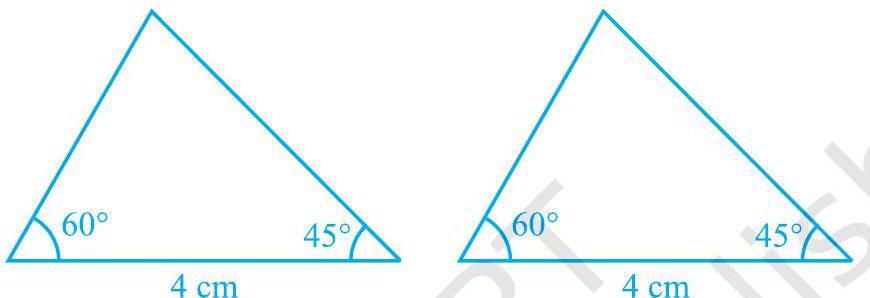
आकृति 7.11
इन दोनों त्रिभुजों को काटिए और एक त्रिभुज को दूसरे के ऊपर रखिए। आप क्या देखते हैं? देखिए कि एक त्रिभुज दूसरे त्रिभुज को पूर्णतया ढक लेता है, अर्थात् दोनों त्रिभुज सर्वांगसम हैं। कुछ और त्रिभुजों को लेकर इस क्रियाकलाप को दोहराइए। आप देखेंगे कि त्रिभुजों की सर्वांगसमता के लिए, दो कोणों और उनकी अंतर्गत भुजा की समता पर्याप्त है।
यह परिणाम कोण-भुजा-कोण (Angle-Side-Angle) कसौटी है और इसे ASA सर्वांगसमता कसौटी लिखा जाता है। आप पिछली कक्षाओं में, इसकी सत्यता की जाँच कर चुके हैं। आइए इस परिणाम को सिद्ध करें।
चूँकि इस परिणाम को सिद्ध किया जा सकता है, इसलिए इसे एक प्रमेय (theorem) कहा जाता है। इसे सिद्ध करने के लिए, हम SAS सर्वांगसमता नियम का प्रयोग करेंगे।
प्रमेय 7.1 (ASA सर्वांगसमता नियम) : दो त्रिभुज सर्वांगसम होते हैं, यदि एक त्रिभुज के दो कोण और उनकी अंतर्गत भुजा दूसरे त्रिभुज के दो कोणों और उनकी अंतर्गत भुजा के बराबर हों।
उपपत्ति : हमें दो त्रिभुज
जिनमें
और
हमें
दोनों त्रिभुजों की सर्वांगसमता के लिए देखिए कि यहाँ तीन स्थितियाँ संभव हैं।
स्थिति (i) : मान लीजिए
अब आप क्या देखते हैं? आप देख सकते हैं कि
अतः,
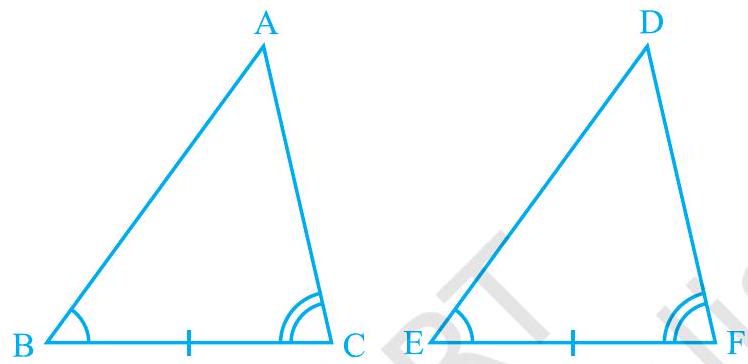
आकृति 7.12
स्थिति (ii) : मान लीजिए, यदि संभव है तो, 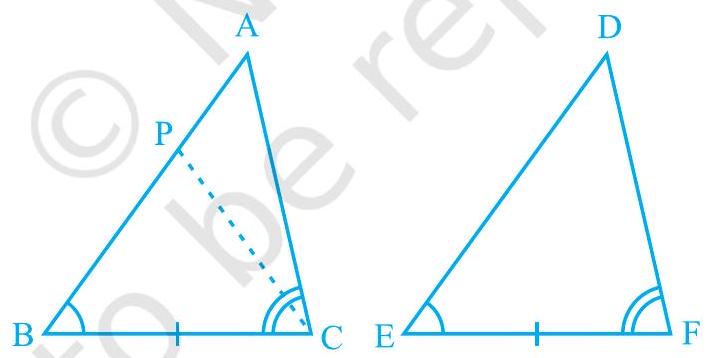
आकृति 7.13
अब
अतः, हम निष्कर्ष निकाल सकते हैं कि
चूँकि दोनों त्रिभुज सर्वांगसम हैं, इसलिए इनके संगत भाग बराबर होने चाहिए।
अतः,
परन्तु हमें दिया है कि
अतः,
परन्तु क्या यह संभव है?
यह तभी संभव है, जब
या
अतः,
स्थिति (iii) : यदि
अब मान लीजिए कि दो त्रिभुजों में दो कोणों के युग्म और संगत भुजाओं का एक युग्म बराबर हैं, परन्तु ये भुजाएँ बराबर कोणों के युग्मों की अंतर्गत भुजाएँ नहीं हैं। क्या ये त्रिभुज अभी भी सर्वांगसम हैं? आप देखेंगे कि ये त्रिभुज सर्वांगसम हैं। क्या आप इसका कारण बता सकते हैं?
आप जानते हैं कि त्रिभुज के तीनों कोणों का योग
अतः, दो त्रिभुज सर्वांगसम होते हैं, यदि इन त्रिभुजों के दो कोणों के युग्म बराबर हों और संगत भुजाओं का एक युग्म बराबर हो। हम इसे AAS सर्वांगसमता नियम कह सकते हैं।
आइए अब निम्नलिखित क्रियाकलाप करें :
आप ऐसे कितने त्रिभुज खींच सकते हें? वास्तव में, भुजाओं की विभिन्न लंबाइयाँ लेकर हम ऐसे जितने चाहे उतने त्रिभुज खींच सकते हैं (देखिए आकृति 7.14)।
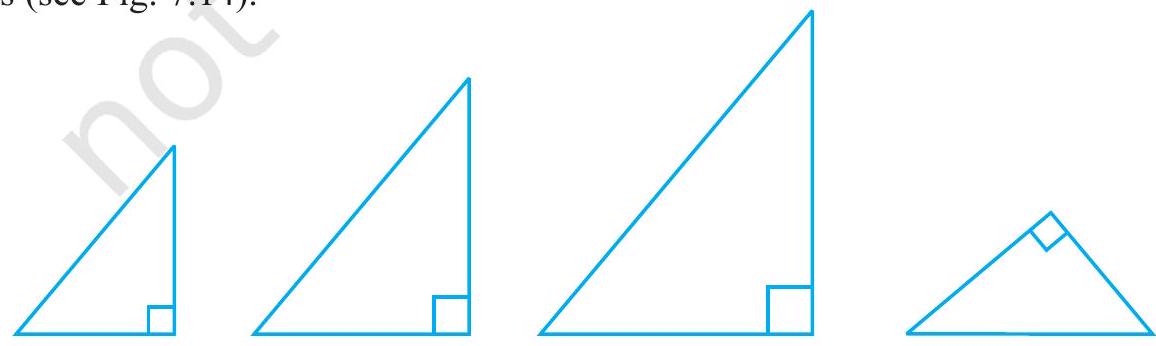
आकृति 7.14
देखिए कि ये त्रिभुज सर्वांगसम हो भी सकते हैं और नहीं भी हो सकते हैं।
अतः, तीन कोणों की समता त्रिभुजों की सर्वांगसमता के लिए पर्याप्त नहीं है। इसलिए, त्रिभुजों की सर्वांगसमता के लिए, तीन बराबर भागों में से एक बराबर भाग भुजा अवश्य होना चाहिए।
आइए अब कुछ और उदाहरण लें।
उदाहरण 3 : रेखाखंड
हल : (i)

आकृति 7.15
अत:,
(ii)
अर्थात्
प्रश्नावली 7.1
1. चतुर्भुज
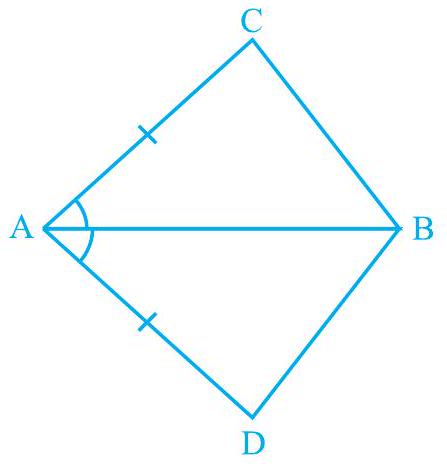
आकृति 7.16
Show Answer
Missing2.
(i)
(ii)
(iii)
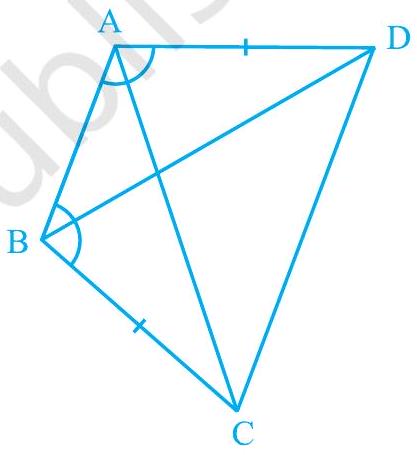
Show Answer
Missing3. एक रेखाखंड
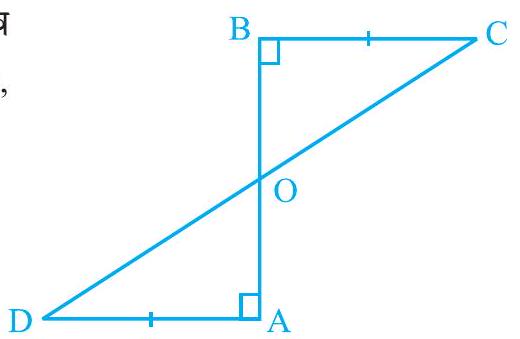
Show Answer
Missing4.
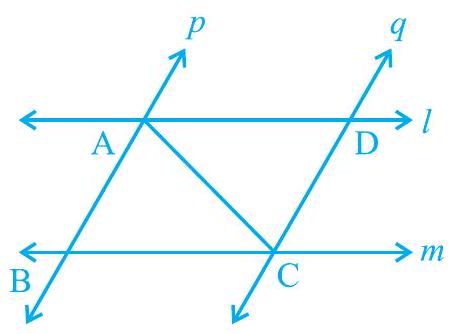
आकृति 7.19
Show Answer
Missing5. रेखा
(i)
(ii)

आकृति 7.20
Show Answer
Missing6. आकृति 7.21 में,

आकृति 7.21
Show Answer
Missing7.
(i)
(ii)
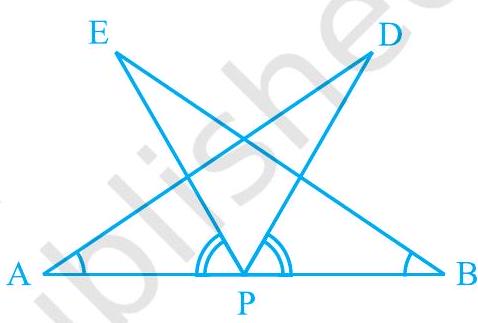
आकृति 7.22
Show Answer
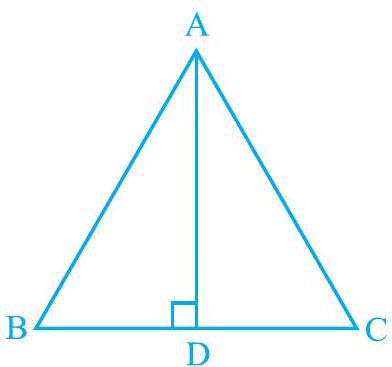
Missing8. एक समकोण त्रिभुज
(i)
(ii)
(iii)
(iv)
आकृति 7.23
Show Answer
Missing7.4 एक त्रिभुज के कुछ गुण
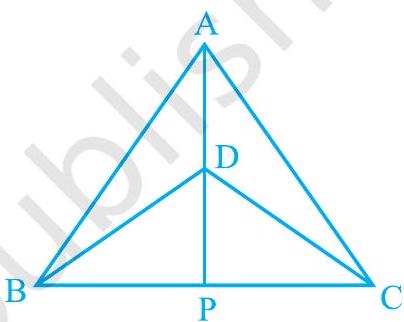
पिछले अनुच्छेद में, आपने त्रिभुजों की सर्वांगसमता की दो कसौटियों का अध्ययन किया है। आइए इन परिणामों का एक ऐसे त्रिभुज के कुछ गुणों का अध्ययन करने में प्रयोग करें जिसकी दो भुजाएँ बराबर होती हैं।
नीचे दिया गया क्रियाकलाप कीजिए:
एक त्रिभुज की रचना कीजिए जिसकी दो भुजाएँ बराबर हों। मान लीजिए दो भुजाएँ

आकृति 7.24
क्या आपको याद है कि इस त्रिभुज को क्या कहते हैं?
एक त्रिभुज जिसकी दो भुजाएँ बराबर हों समद्विबाहु त्रिभुज (isosceles triangle) कहलाता है। अतः, आकृति 7.24 का
अब
विभिन्न भुजाओं वाले अन्य समद्विबाहु त्रिभुज लेकर इस क्रियाकलाप को दोहराइए। आप देख सकते हैं कि ऐसे प्रत्येक त्रिभुज में बराबर भुजाओं के सम्मुख (सामने के) कोण बराबर हैं।
यह एक अति महत्वपूर्ण परिणाम है और प्रत्येक समद्विबाहु त्रिभुज के लिए सत्य है। इसे नीचे दशाई विधि के अनुसार सिद्ध किया जा सकता है:
प्रमेय 7.2 : एक समद्विबाहु त्रिभुज की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं। इस परिणाम को कई विधियों से सिद्ध किया जा सकता है। इनमें से एक उपपत्ति नीचे दी जा रही है।
उपपत्ति : हमें एक समद्विबाहु

आकृति 7.25
क्या इसका विलोम भी सत्य है? अर्थात्
यदि किसी त्रिभुज के दो कोण बराबर हों, तो क्या हम निष्कर्ष निकाल सकते हैं कि उनकी सम्मुख भुजाएँ भी बराबर होंगी?
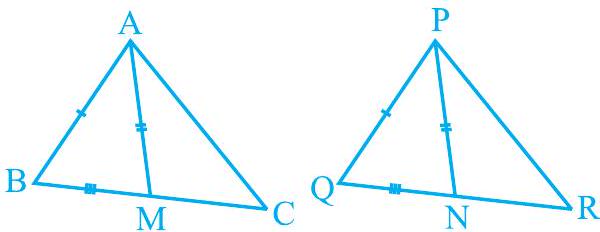
नीचे दिया क्रियाकलाप कीजिए :
एक

आकृति 7.26
त्रिभुज
देखिए कि
अतः,
इसी क्रियाकलाप को ऐसे ही कुछ अन्य त्रिभुज लेकर दोहराइए। प्रत्येक बार आप देखेंगे कि एक त्रिभुज के बराबर कोणों की सम्मुख भुजाएँ बराबर हैं। अतः, हम निम्न प्रमेय प्राप्त करते हैं :
प्रमेय 7.3 : किसी त्रिभुज के बराबर कोणों की सम्मुख भुजाएँ बराबर होती हैं।
यह प्रमेय 7.2 का विलोम है।
आप इस प्रमेय को ASA सर्वांगसमता नियम का प्रयोग करके सिद्ध कर सकते हैं। आइए इन परिणामों को स्पष्ट करने के लिए कुछ उदाहरण लें।
उदाहरण 4 :

आकृति 7.27
हल :
इसी कारण
उदाहरण 5 :

आकृति 7.28
हल :
उदाहरण 6 : एक समद्विबाहु त्रिभुज

आकृति 7.29
हल :
साथ ही,
इसलिए,
अर्थात्,
अतः,
इससे प्राप्त होता है:
प्रश्नावली 7.2
1. एक समद्विबाहु त्रिभुज
(i)
(ii)
Show Answer
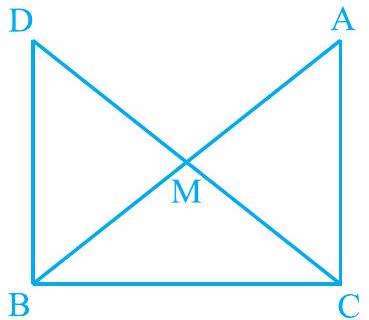
Missing2.
आकृति 7.30
Show Answer
Missing3.
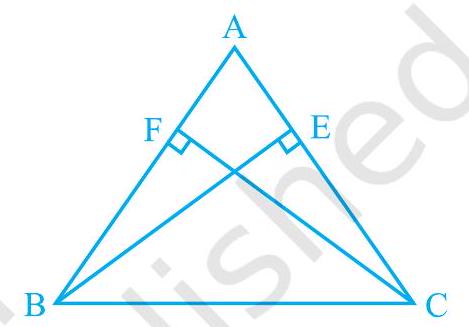
आकृति 7.31
Show Answer
Missing4.
(i)
(ii)
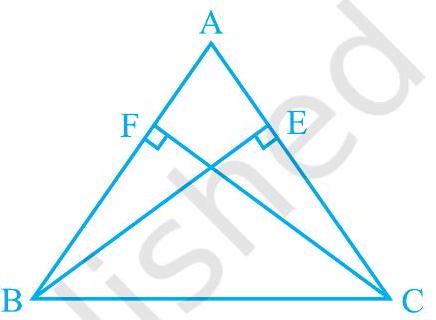
आकृति 7.32
Show Answer
Missing5.
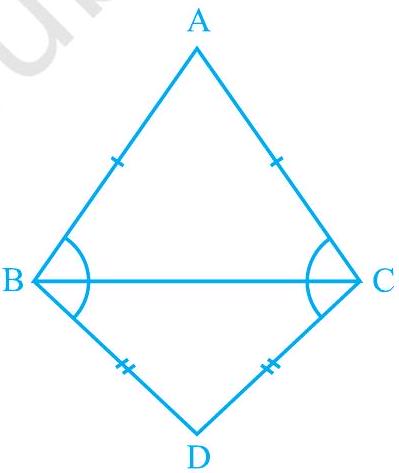
आकृति 7.33
Show Answer
Missing6.
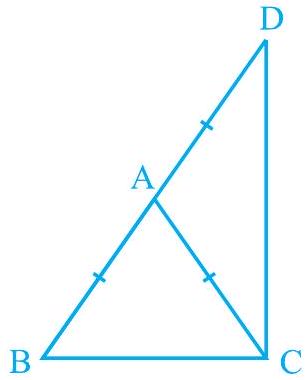
आकृति 7.34
Show Answer
Missing7.
Show Answer
Missing8. दर्शाइए कि किसी समबाहु त्रिभुज का प्रत्येक कोण
Show Answer
Missing7.5 त्रिभुजों की सर्वांगसमता के लिए कुछ और कसौटियाँ
आप इस अध्याय में, पहले यह देख चुके हैं कि एक त्रिभुज के तीनों कोणों के दूसरे त्रिभुज के तीनों कोणों के बराबर होने पर दोनों त्रिभुजों का सर्वांगसम होना आवश्यक नहीं है। आप सोच सकते हैं कि संभवतः एक त्रिभुज की तीनों भुजाओं के दूसरे त्रिभुज की तीनों भुजाओं के बराबर होने पर त्रिभुज सर्वांगसम हो जाएँ। आप यह पिछली कक्षाओं में पढ़ चुके हैं कि ऐसी स्थिति में त्रिभुज नि:संदेह सर्वांगसम होते हैं।
इस धारणा को निश्चित करने के लिए, 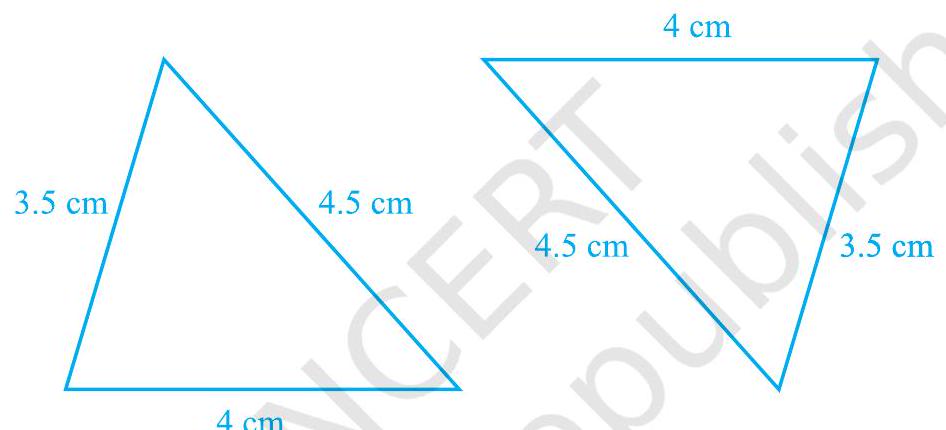
आकृति 7.35
इस क्रियाकलाप को कुछ अन्य त्रिभुज खींचकर दोहराइए। इस प्रकार, हम सर्वांगसमता के एक और नियम पर पहुँच जाते हैं:
प्रमेय 7.4 (SSS सर्वांगसमता नियम) : यदि एक त्रिभुज की तीनों भुजाएँ एक अन्य त्रिभुज की तीनों भुजाओं के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं।
एक उपयुक्त रचना करके, इस प्रमेय को सिद्ध किया जा सकता है।
आप SAS सर्वांगसमता नियम में पहले ही देख चुके हैं कि बराबर कोणों के युग्म संगत बराबर भुजाओं के युग्मों के बीच में (अंतर्गत) होने चाहिए और यदि ऐसा नहीं हो, तो दोनों त्रिभुज सर्वांगसम नहीं भी हो सकते हैं।
इस क्रियाकलाप को कीजिए :
दो समकोण त्रिभुज ऐसे खींचिए जिनमें प्रत्येक का कर्ण 5 सेमी और एक भुजा

आकृति 7.36
इन्हें काटिए और एक दूसरे पर इस प्रकार रखिए कि इनकी बराबर भुजाएँ एक दूसरे पर आएँ। यदि आवश्यक हो, तो त्रिभुजों को घुमाइए। आप क्या देखते हैं?
आप देखते हैं कि दोनों त्रिभुज एक दूसरे को पूर्णतया ढक लेते हैं और इसीलिए ये सर्वांगसम हैं। यही क्रियाकलाप समकोण त्रिभुजों के अन्य युग्म लेकर दोहराइए। आप क्या देखते हैं?
आप पाएँगे कि दोनों समकोण त्रिभुज सर्वांगसम होंगे, यदि उनके कर्ण बराबर हों और भुजाओं का एक युग्म बराबर हो। आप इस तथ्य की जाँच पिछली कक्षाओं में कर चुके हैं। ध्यान दीजिए कि इस स्थिति में समकोण अंतर्गत कोण नहीं है।
इस प्रकार, आप निम्नलिखित सर्वांगसमता नियम पर पहुँच गए हैं:
प्रमेय 7.5 (RHS सर्वांगसमता नियम ) : यदि दो समकोण त्रिभुजों में, एक त्रिभुज का कर्ण और एक भुजा क्रमशः दूसरे त्रिभुज के कर्ण और एक भुजा के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं।
ध्यान दीजिए कि यहाँ RHS समकोण (Right angle) - कर्ण (Hypotenuse) - भुजा (Side) को दर्शाता है।
आइए अब कुछ उदाहरण लें।
उदाहरण 7 :
हल : आपको

आकृति 7.37
इन त्रिभुजों में,
अत:,
इसलिए,
अब
अत:,
इसलिए,
और
(1) और (2) से, आप निष्कर्ष निकाल सकते हैं कि रेखा
[ध्यान दीजिए कि
यह इस कारण है कि इनसे हमें SSA नियम प्राप्त होता है, जो त्रिभुजों की सर्वांगसमता के लिए सदैव मान्य नहीं है। साथ ही, कोण बराबर भुजाओं के अंतर्गत नहीं है।]
आइए कुछ और उदाहरण लें।
उदाहरण 8 : बिंदु
हल : आपको दिया है कि रेखाएँ
आपको दर्शाना है कि
अब,

आकृति 7.38
अत:
इसलिए,
ध्यान दीजिए कि यह परिणाम प्रश्नावली 7.1 के प्रश्न 5 में सिद्ध किए गए परिणाम का विलोम है।
प्रश्नावली 7.3
1.
(i)
(ii)
(iii)
(iv)
आकृति 7.39
Show Answer
Missing2.
(i)
(ii)
Show Answer
Missing3. एक त्रिभुज
(i)
(ii)
आकृति 7.40
Show Answer
Missing4.
Show Answer
Missing5.
Show Answer
Missing7.6 सारांश
इस अध्याय में, आपने निम्न बिंदुओं का अध्ययन किया है:
1. दो आकृतियाँ सर्वांगसम होती हैं, यदि उनका एक ही आकार हो और एक ही माप हो।
2. समान त्रिज्याओं वाले दो वृत्त सर्वांगसम होते हैं।
3. समान भुजाओं वाले दो वर्ग सर्वांगसम होते हैं।
4. यदि त्रिभुज
5. यदि एक त्रिभुज की दो भुजाएँ और अंतर्गत कोण दूसरे त्रिभुज की दो भुजाओं और अंतर्गत कोण के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं (SAS सर्वांगसमता नियम)।
6. यदि एक त्रिभुज के दो कोण और अंतर्गत भुजा दूसरे त्रिभुज के दो कोणों और अंतर्गत भुजा के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं (ASA सर्वांगसमता नियम)।
7. यदि एक त्रिभुज के दो कोण और एक भुजा दूसरे त्रिभुज के दो कोणों और संगत भुजा के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं (AAS सर्वांगसमता नियम)।
8. त्रिभुज की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।
9. त्रिभुज के बराबर कोणों की सम्मुख भुजाएँ बराबर होती हैं।
10. किसी समबाहु त्रिभुज का प्रत्येक कोण
11. यदि एक त्रिभुज की तीनों भुजाएँ दूसरे त्रिभुज की तीनों भुजाओं के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं (SSS सर्वांगसमता नियम)।
12. यदि दो समकोण त्रिभुजों में, एक त्रिभुज का कर्ण और एक भुजा क्रमशः दूसरे त्रिभुज के कर्ण और एक भुजा के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं (RHS सर्वांगसमता नियम)।










