अध्याय 06 रेखाएँ और कोण
6.1 भूमिका
अध्याय 5 में, आप पढ़ चुके हैं कि एक रेखा को खींचने के लिए न्यूनतम दो बिंदुओं की आवश्यकता होती है। आपने कुछ अभिगृहीतों (axioms) का भी अध्ययन किया है और उनकी सहायता से कुछ अन्य कथनों को सिद्ध किया है। इस अध्याय में, आप कोणों के उन गुणों का अध्ययन करेंगे जब दो रेखाएँ परस्पर प्रतिच्छेद करती हैं और कोणों के उन गुणों का भी अध्ययन करेंगे जब एक रेखा दो या अधिक समांतर रेखाओं को भिन्न-भिन्न बिंदुओं पर काटती है। साथ ही, आप इन गुणों का निगमनिक तर्कण (deductive reasoning) द्वारा कुछ कथनों को सिद्ध करने में भी प्रयोग करेंगे (देखिए परिशिष्ट 1)। आप पिछली कक्षाओं में इन कथनों की कुछ क्रियाकलापों द्वारा जाँच (पुष्टि) कर चुके हैं।
आप अपने दैनिक जीवन में समतल पृष्ठों के किनारों (edges) के बीच बने अनेक प्रकार के कोण देखते हैं। समतल पृष्ठों का प्रयोग करके, एक ही प्रकार के मॉडल बनाने के लिए, आपको कोणों के बारे में विस्तृत जानकारी की आवश्यकता होती है। उदाहरणार्थ, आप अपने विद्यालय की प्रदर्शिनी के लिए बाँसों का प्रयोग करके एक झोंपड़ी का मॉडल बनाना चाहते हैं। सोचिए, आप इसे कैसे बनाएँगे। कुछ बाँसों को आप परस्पर समांतर रखेंगे और कुछ को तिरछा रखेंगे। जब एक आर्किटेक्ट (architect) एक बहुतलीय भवन के लिए एक रेखाचित्र खींचता है, तो उसे विभिन्न कोणों पर प्रतिच्छेदी और समांतर रेखाएँ खींचनी पड़ती हैं। क्या आप सोचते हैं कि वह रेखाओं और कोणों के ज्ञान के बिना इस भवन की रूपरेखा खींच सकता है?
विज्ञान में, आप प्रकाश के गुणों का किरण आरेख (ray diagrams) खींच कर अध्ययन करते हैं। उदाहरणार्थ, प्रकाश के अपवर्तन (refraction) गुण का अध्ययन करने के लिए, जब प्रकाश की किरणें एक माध्यम (medium) से दूसरे माध्यम में प्रवेश करती हैं, आप प्रतिच्छेदी रेखाओं और समांतर रेखाओं के गुणों का प्रयोग करते हैं। जब एक पिंड पर दो या अधिक बल कार्य कर रहे हों, तो आप इन बलों का उस पिंड पर परिणामी बल ज्ञात करने के लिए, एक ऐसा आरेख खींचते हैं जिसमें बलों को दिष्ट रेखाखंडों (directed line segments) द्वारा निरूपित किया जाता है। उस समय, आपको उन कोणों के बीच संबंध जानने की आवश्यकता होगी जिनकी किरणें (अथवा रेखाखंड) परस्पर समांतर या प्रतिच्छेदी होंगी। एक मीनार की ऊँचाई ज्ञात करने अथवा किसी जहाज की एक प्रकाश पुंज (light house) से दूरी ज्ञात करने के लिए, हमें क्षैतिज और दृष्टि रेखा (line of sight) के बीच बने कोण की जानकारी की आवश्यकता होगी। प्रचुर मात्रा में ऐसे उदाहरण दिए जा सकते हैं जहाँ रेखाओं और कोणों का प्रयोग किया जाता है। ज्यामिति के आने वाले अध्यायों में, आप रेखाओं और कोणों के इन गुणों का अन्य उपयोगी गुणों को निगमित (निकालने) करने में प्रयोग करेंगे।
आइए पहले हम पिछली कक्षाओं में रेखाओं और कोणों से संबंधित पढ़े गए पदों और परिभाषाओं का पुनर्विलोकन करें।
6.2 आधारभूत पद और परिभाषाएँ
याद कीजिए कि एक रेखा का वह भाग जिसके दो अंत बिंदु हों एक रेखाखंड कहलाता है और रेखा का वह भाग जिसका एक अंत बिंदु हो एक किरण कहलाता है। ध्यान दीजिए कि रेखाखंड
यदि तीन या अधिक बिंदु एक ही रेखा पर स्थित हों, तो वे संरेख बिंदु (collinear points) कहलाते हैं, अन्यथा वे असंरेख बिंदु (non-collinear points) कहलाते हैं।
याद कीजिए कि जब दो किरणें एक ही अंत बिंदु से प्रारम्भ होती हैं, तो एक कोण (angle) बनता है। कोण को बनाने वाली दोनों किरणें कोण की भुजाएँ (arms या sides) कहलाती हैं और वह उभयनिष्ठ अंत बिंदु कोण का शीर्ष (vertex) कहलाता है। आप पिछली कक्षाओं में, विभिन्न प्रकार के कोणों जैसे न्यून कोण (acute angle), समकोण (right angle), अधिक कोण (obtuse angle), ॠजु कोण (straight angle) और प्रतिवर्ती कोण (reflex angle) के बारे में पढ़ चुके हैं (देखिए आकृति 6.1)।

आकृति 6.1 : कोणों के प्रकार
एक न्यून कोण का माप
आप पिछली कक्षाओं में आसन्न कोणों (adjacent angles) के बारे में भी पढ़ चुके हैं (देखिए आकृति 6.2)। दो कोण आसन्न कोण (adjacent angles) कहलाते हैं, यदि उनमें एक उभयनिष्ठ शीर्ष हो, एक उभयनिष्ठ भुजा हो और उनकी वे भुजाएँ जो उभयनिष्ठ नहीं हैं, उभयनिष्ठ भुजा के विपरीत ओर स्थित हों। आकृति 6.2 में,

आकृति 6.2 : आसन्न कोण अतः हम लिख सकते हैं कि
ध्यान दीजिए कि
यदि आकृति 6.2 में, अउभयनिष्ठ भुजाएँ

आकृति 6.3 : कोणों का रैखिक युग्म
आप शीर्षाभिमुख कोणों (vertically opposite angles) को भी याद कर सकते हैं, जो दो रेखाओं, मान लीजिए,

आकृति 6.4 : शीर्षाभिमुख कोण युग्म
इनमें से एक शीर्षाभिमुख कोण युग्म
6.3 प्रतिच्छेदी रेखाएँ और अप्रतिच्छेदी रेखाएँ
एक कागज़ पर दो भिन्न रेखाएँ

आकृति 6.5 : दो रेखाएँ खींचने के विभिन्न प्रकार
(ii) अप्रतिच्छेदी (समांतर) रेखाएँ
रेखा की इस अवधारणा को भी याद कीजिए कि वह दोनों दिशाओं में अनिश्चित रूप से विस्तृत होती है। रेखाएँ
6.4 कोणों के युग्म
अनुच्छेद 6.2 में, आप कोणों के कुछ युग्मों जैसे पूरक कोण, संपूरक कोण, आसन्न कोण, कोणों का रैखिक युग्म, इत्यादि की परिभाषाओं के बारे में पढ़ चुके हैं। क्या आप इन कोणों में किसी संबंध के बारे में सोच सकते हैं? आइए अब उन कोणों में संबंध पर विचार करें जिन्हें कोई किरण किसी रेखा पर स्थित होकर बनाती है, जैसा कि आकृति 6.6 में दर्शाया गया है। रेखा को

आकृति 6.6 :
क्या हम
हाँ! (क्यों? अनुच्छेद 6.2 में दिए आसन्न कोणों को देखिए।)
क्या (1) ओर (2) से, आप कह सकते हैं कि
उपरोक्त चर्चा के आधार पर, हम निम्न अभिगृहीत को लिख सकते हैं:
अभिगृहीत 6.1 : यदि एक किरण एक रेखा पर खड़ी हो, तो इस प्रकार बने दोनों आसन्न कोणों का योग
याद कीजिए कि जब दो आसन्न कोणों का योग
अभिगृहीत 6.1 में यह दिया है कि ‘एक किरण एक रेखा पर खड़ी हो’। इस दिए हुए से, हमने निष्कर्ष निकाला कि इस प्रकार बने दोनों आसन्न कोणों का योग
(A) यदि दो आसन्न कोणों का योग
अब आप देखते हैं कि अभिगृहीत 6.1 और कथन (A) एक दूसरे के विपरीत हैं। हम इनमें से प्रत्येक को दूसरे का विलोम (converse) कहते हैं। हम यह नहीं जानते कि कथन (A) सत्य है या नहीं। आइए इसकी जाँच करें। विभिन्न मापों के, आकृति 6.7 में दर्शाए अनुसार, आसन्न कोण खींचिए। प्रत्येक स्थिति में, अउभयनिष्ठ भुजाओं में से एक भुजा के अनुदिश एक पटरी (ruler) रखिए। क्या दूसरी भुजा भी इस पटरी के अनुदिश स्थित है?

आकृति 6.7 : विभिन्न मापों के आसन्न कोण
आप पाएँगे कि केवल आकृति 6.7 (iii) में ही दोनों अउभयनिष्ठ भुजाएँ पटरी के अनुदिश हैं, अर्थात्
अभिगृहीत 6.2 : यदि दो आसन्न कोणों का योग
स्पष्ट कारणों से, उपरोक्त दोनों अभिगृहीतों को मिला कर रैखिक युग्म अभिगृहीत (Linear Pair Axiom) कहते हैं।
आइए अब उस स्थिति की जाँच करें जब दो रेखाएँ प्रतिच्छेद करती हैं।
पिछली कक्षाओं से आपको याद होगा कि यदि दो रेखाएँ परस्पर प्रतिच्छेद करें, तो शीर्षाभिमुख कोण बराबर होते हैं। आइए अब इस परिणाम को सिद्ध करें। एक उपपत्ति (proof) में निहित अवयवों के लिए, परिशिष्ट 1 को देखिए और नीचे दी हुई उपपत्ति को पढ़ते समय इन्हें ध्यान में रखिए।
प्रमेय 6.1 : यदि दो रेखाएँ परस्पर प्रतिच्छेद करती हैं, तो शीर्षाभिमुख कोण बराबर होते हैं।
उपपत्ति : उपरोक्त कथन में यह दिया है कि दो रेखाएँ परस्पर प्रतिच्छेद करती हैं। अतः मान लीजिए कि
(i)

आकृति 6.8 : शीर्षाभिमुख कोण
हमें सिद्ध करना है कि
और
अब किरण
अत:
क्या हम
(1) और (2) से, हम लिख सकते हैं कि:
इससे निष्कर्ष निकलता है कि
इसी प्रकार, सिद्ध किया जा सकता है कि
आइए अब रैखिक युग्म अभिगृहीत और प्रमेय 6.1 पर आधारित कुछ उदाहरण हल करें।
उदाहरण 1 : आकृति 6.9 में, रेखाएँ
हल :
(रैखिक युग्म के कोण)
परन्तु,
अतः,

इसी प्रकार,
उदाहरण 2 : आकृति 6.10 में, किरण
हल : किरण OS रेखा POQ पर खड़ी है।
अत:,
परन्तु,
अतः,
इसलिए,
अब किरण

आकृति 6.10
इसी प्रकार,
अब,
उदाहरण 3 : आकृति 6.11 में,
हल : आकृति 6.11 में, आपको किरणों

आकृति 6.11 हो (देखिए आकृति 6.12)।
अब किरण
अत:,
(रैखिक युग्म अभिगृहीत)
इसी प्रकार, किरण OS रेखा TOQ पर खड़ी है।
अतः,
परन्तु
अतः,(2) निम्न हो जाती है :

आकृति 6.12
अब, (1) और (3) को जोड़ने पर, आपको प्राप्त होगा:
परन्तु
अतः,(4) निम्न हो जाती है :
प्रश्नावली 6.1
1. आकृति 6.13 में, रेखाएँ
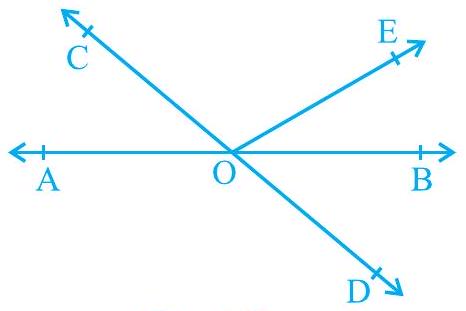
आकृति 6.13
Show Answer
Missing2. आकृति 6.14 में, रेखाएँ
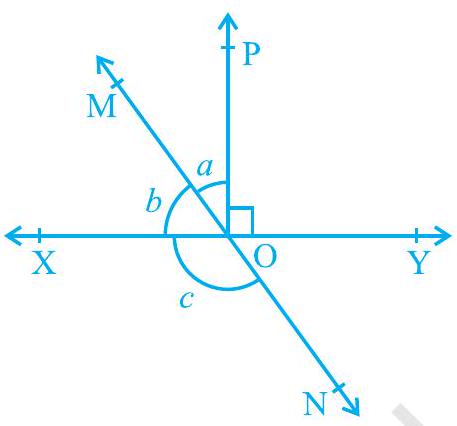
आकृति 6.14
Show Answer
Missing3. आकृति 6.15 में, यदि
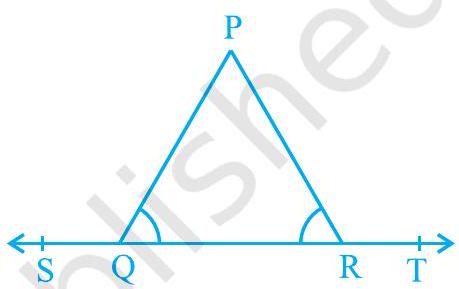
आकृति 6.15
Show Answer
Missing4. आकृति 6.16 में, यदि
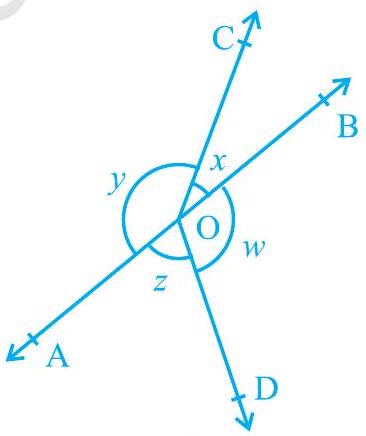
आकृति 6.16
Show Answer
Missing5. आकृति 6.17 में,
Show Answer
Missing6. यह दिया है कि

आकृति 6.17
Show Answer
Missing6.5 एक ही रेखा के समांतर रेखाएँ
यदि दो रेखाएँ एक ही रेखा के समांतर हों, तो क्या वे परस्पर समांतर होंगी? आइए इसकी जाँच करें। आकृति 6.18 को देखिए, जिसमें
अत:
इसलिए,
परन्तु
अतः, आप कह सकते हैं कि
(संगत कोण अभिगृहीत का विलोम)
इस परिणाम को एक प्रमेय के रूप में निम्न प्रकार व्यक्त किया जा सकता है:

आकृति 6.18
प्रमेय 6.6 : वे रेखाएँ जो एक ही रेखा के समांतर हों, परस्पर समांतर होती हैं।
टिप्पणी: उपरोक्त गुण को दो से अधिक रेखाओं के लिए भी लागू किया जा सकता है।
आइए अब समांतर रेखाओं से संबंधित कुछ प्रश्न हल करें:
उदाहरण 4 : आकृति 6.19 में, यदि

आकृति 6.19
हल : यहाँ हमें

आकृति 6.20
अब,
परन्तु,
अतः,
अब,
अतः,
(1) और (2) को जोड़ने पर, आपको प्राप्त होगा :
अर्थात,
उदाहरण 5 : यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार प्रतिच्छेद करे कि संगत कोणों के एक युग्म के समद्विभाजक परस्पर समांतर हों, तो सिद्ध कीजिए कि दोनों रेखाएँ भी परस्पर समांतर होती हैं।
हल : आकृति 6.21 में, एक तिर्यक रेखा
हमें सिद्ध करना है कि
यह दिया है कि किरण
अत:
इसी प्रकार किरण
अतः,

आकृति 6.21
परन्तु,
अतः,
(3) में, (1) और (2) को प्रतिस्थापित करने पर, आपको प्राप्त होगा:
अर्थात्,
परन्तु, ये तिर्यक रेखा
अत :
PQ || RS
(संगत कोण अभिगृहीत का विलोम)
उदाहरण 6 : आकृति 6.22 में,
हल :
अत:,
पुन: x=y
(
इसलिए,
अब चूँकि

आकृति 6.22
अत:,
इसलिए,
जिससे,
प्रश्नावली 6.2
1. आकृति 6.23 में, यदि
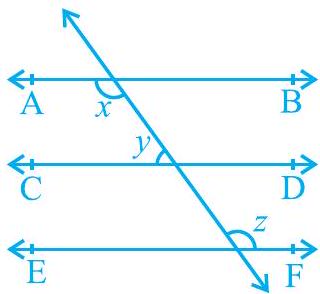
आकृति 6.23
Show Answer
Missing2. आकृति 6.24 में, यदि
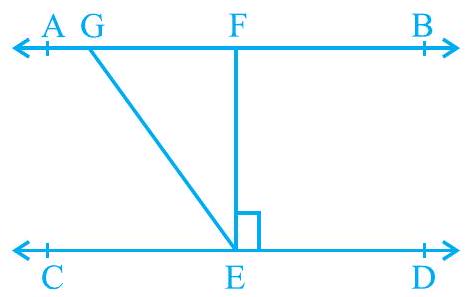
आकृति 6.24
Show Answer
Missing- आकृति 6.25 में, यदि
[संकेत : बिंदु
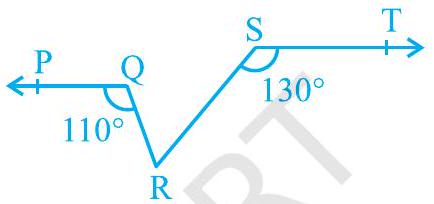
आकृति 6.25
Show Answer
Missing4. आकृति 6.26 में, यदि
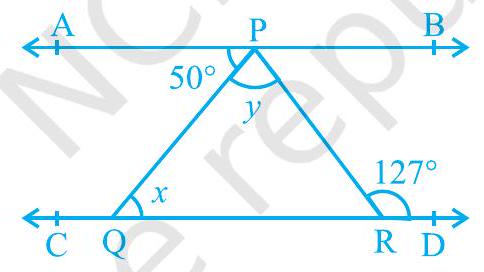
आकृति 6.26
Show Answer
Missing5. आकृति 6.27 में,
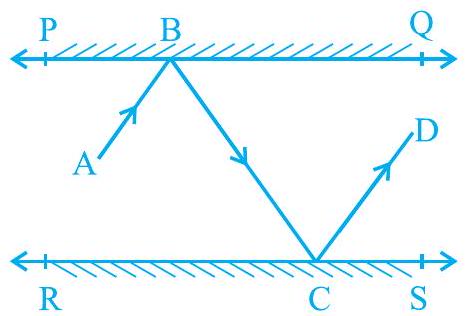
आकृति 6.27
Show Answer
Missing6.6 सारांश
इस अध्याय में, आपने निम्न बिंदुओं का अध्ययन किया है:
1. यदि एक किरण एक रेखा पर खड़ी हो, तो इस प्रकार बने दोनों आसन्न कोणों का योग
2. यदि दो रेखाएँ परस्पर प्रतिच्छेद करें, तो शीर्षाभिमुख कोण बराबर होते हैं।
3. वे रेखाएँ जो एक ही रेखा के समांतर होती हैं परस्पर समांतर होती हैं।










