अध्याय 09 क्षेत्रमिति
9.1 भूमिका
हम अध्ययन कर चुके हैं कि किसी बंद समतल आकृति की सीमा के चारों ओर की दूरी उसका परिमाप कहलाता है और उस आकृति द्वारा घिरे हुए क्षेत्र को उसका क्षेत्रफल कहते हैं। हम त्रिभुज, आयत, वृत्त इत्यादि विभिन्न समतल आकृतियों का परिमाप और क्षेत्रफल ज्ञात करना सीख चुके हैं तथा आयताकार आकार के किनारों अथवा पगडंडियों का क्षेत्रफल भी सीख चुके हैं।
इस अध्याय में हम चतुर्भुज जैसी दूसरी बंद आकृतियों के क्षेत्रफल एवं परिमाप से संबंधित समस्याएँ हल करने का प्रयत्न करेंगे। हम घन, घनाभ और बेलन जैसे ठोसों के पृष्ठीय क्षेत्रफल एवं आयतन का भी अध्ययन करेंगे।
9.2 बहुभुज का क्षेत्रफल
हम एक चतुर्भुज को त्रिभुजों में खंडित करते हैं और इसका क्षेत्रफल ज्ञात करते हैं। इसी प्रकार की विधि बहुभुज का क्षेत्रफल ज्ञात करने के लिए उपयोग की जा सकती है। एक पंचभुज के लिए निम्नलिखित पर विचार कीजिए (आकृति 9.1, 9.2)

विकर्ण

एक विकर्ण
प्रयास कीजिए
(i) निम्नलिखित बहुभुजों (आकृति 9.3) का क्षेत्रफल ज्ञात करने के लिए इन्हें विभिन्न भागों (त्रिभुजों एवं समलंबों) में विभाजित कीजिए।

(ii) बहुभुज
को विभिन्न भागों में बाँटा गया है जैसा कि आकृति 9.4 में दर्शाया गया है। यदि और लंब , तो इसका क्षेत्रफल ज्ञात कीजिए। बहुभुज का क्षेत्रफल का क्षेत्रफल .
का क्षेत्रफल .. समलंब का क्षेत्रफल 
का क्षेत्रफल का क्षेत्रफल इसलिए बहुभुज का क्षेत्रफल . (iii) यदि
, तो बहुभुज (आकृति 9.5) का क्षेत्रफल ज्ञात कीजिए। NA, OC, एवं विकर्ण पर खींचे गए लंब हैं। 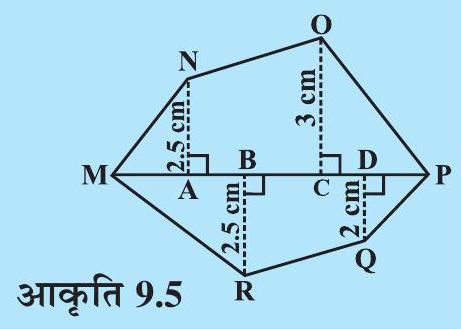
उदाहरण 1 : समलंब के आकार के एक खेत का क्षेत्रफल
हल : समलंब की समांतर भुजाओं में से एक की लंबाई
समलंब का दिया हुआ क्षेत्रफल
इसलिए
अथवा
अतः समलंब की दूसरी समांतर भुजा
उदाहरण 2 : एक समचतुर्भुज का क्षेत्रफल
हल : मान लीजिए एक विकर्ण की लंबाई
और
इसलिए,
अतः,
इस प्रकार दूसरे विकर्ण की लंबाई
उदाहरण 3: MNOPQR (आकृति 9.6) एक षड्भुज है जिसकी प्रत्येक भुजा

हल : अमन की विधि
क्योंकि यह एक षड्भुज है इसलिए

अब समलंब MNQR का क्षेत्रफल

आकृति 9.9
इसलिए षड्भुज MNOPQR का क्षेत्रफल
रिधिमा की विधि :
आप इन त्रिभुजों को काटकर और एक-दूसरे के ऊपर रखकर इसका सत्यापन कर सकते हैं।
अब, षड्भुज
प्रश्नावली 9.1
1. एक मेज़ के ऊपरी पृष्ठ (सतह) का आकार समलंब जैसा है। यदि इसकी समांतर भुजाएँ

2. एक समलंब का क्षेत्रफल
3. एक समलंब के आकार के खेत

4. एक चतुर्भुज आकार के खेत का विकर्ण

5. किसी समचतुर्भुज के विकर्ण
6. एक समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसकी भुजा
7. किसी भवन के फर्श में समचतुर्भुज के आकार की 3000 टाइलें हैं और इनमें से प्रत्येक के विकर्ण
8. मोहन एक समलंब के आकार का खेत खरीदना चाहता है। इस खेत की नदी के साथ वाली भुजा सड़क के साथ वाली भुजा के समांतर हैं और लंबाई में दुगुनी है। यदि इस खेत का क्षेत्रफल

9. एक ऊपर उठे हुए चबूतरे का ऊपरी पृष्ठ अष्टभुज के आकार का है। जैसा कि आकृति में दर्शाया गया है। अष्टभुजी पृष्ठ का क्षेत्रफल ज्ञात कीजिए।

10. एक पंचभुज आकार का बगीचा है जैसा कि आकृति में दर्शाया गया है। इसका क्षेत्रफल ज्ञात करने के लिए ज्योति और कविता ने इसे दो विभिन्न तरीकों से विभाजित किया। दोनों तरीकों का उपयोग करते हुए इस बगीचे का क्षेत्रफल ज्ञात कीजिए। क्या आप इसका क्षेत्रफल ज्ञात करने की कोई और विधि बता सकते हैं?
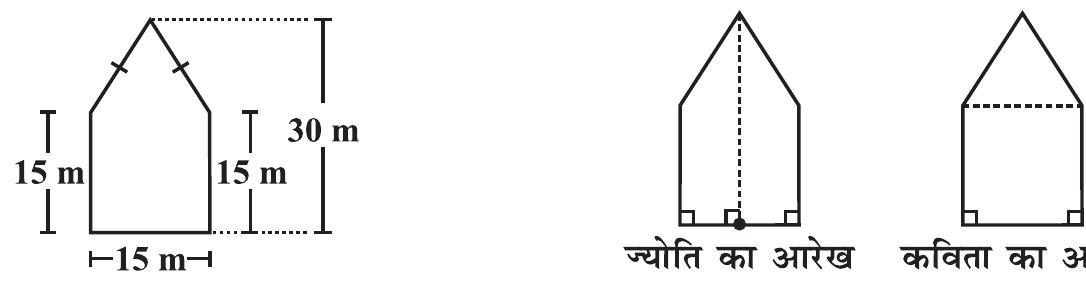
कविता का आरेख
11. संलग्न पिक्चर फ्रेम के आरेख की बाहरी एवं अंतः विमाएँ क्रमशः

9.3 ठोस आकार
आप अपनी पिछली कक्षाओं में अध्ययन कर चुके हैं कि द्विविमीय आकृतियों को त्रिविमीय आकारों के फलकों के रूप में पहचाना जा सकता है। अभी तक हमने जिन ठोसों का अध्ययन किया है उन पर ध्यान दीजिए (आकृति 9.10)।
ध्यान दीजिए कि कुछ आकारों में दो या दो से अधिक समरूप (सर्वांगसम) फलक हैं। उनको नाम दीजिए। कौन से ठोसों में सभी फलक सर्वांगसम हैं?

इन्हें कीजिए
साबुन, खिलौने, मंजन, अल्पाहार इत्यादि प्राय: घनाभकार, घनाकार अथवा बेलनाकार डिब्बों में बंद आते हैं। ऐसे डिब्बों को एकत्रित कीजिए (आकृति 9.11)।



आकृति 9.12
(यह एक लंब वृत्तीय बेलन है।)
अब एक समय में एक प्रकार के डिब्बे को लीजिए। इसके सभी फलकों को काटिए। प्रत्येक फलक के आकार को देखिए और समान फलकों को एक-दूसरे के ऊपर रखकर डिब्बे में फलकों की संख्या ज्ञात कीजिए। अपने प्रेक्षणों को लिखिए।
क्या आपने निम्नलिखित पर ध्यान दिया- बेलन के, सर्वांगसम वृत्ताकार फलक एक-दूसरे के समांतर हैं (आकृति 9.12)। ध्यान दीजिए कि वृत्ताकार फलकों के मध्य बिंदुओं को मिलाने वाला रेखाखंड आधार पर लंब है। ऐसे बेलन लंबवृत्तीय बेलन कहलाते हैं। हम केवल इस प्रकार के बेलनों का ही अध्ययन करेंगे, यद्यपि दूसरे प्रकार के बेलन भी होते हैं (आकृति 9.13)।

आकृति 9.13
(यह एक लंब वृत्तीय बेलन नहीं है।)
सोचिए, चर्चा कीजिए और लिखिए
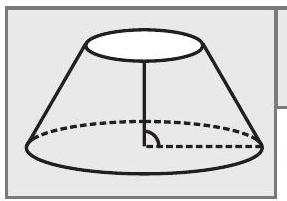
संलग्न आकृति में दर्शाए गए ठोस को बेलन कहना क्यों गलत है?
9.4 घन, घनाभ और बेलन का पृष्ठीय क्षेत्रफल
इमरान, मोनिका और जसपाल क्रमशः समान ऊँचाई वाले घनाभाकार, घनाकार और बेलनाकार डिब्बों को पेंट कर रहे (आकृति 9.14)।

वे यह ज्ञात करने का प्रयास करते हैं कि किसने अधिक क्षेत्रफल को पेंट किया है। हरी उन्हें सुझाव देता है कि प्रत्येक डिब्बे का पृष्ठीय क्षेत्रफल ज्ञात करना उनकी मदद करेगा।
कुल पृष्ठीय क्षेत्रफल ज्ञात करने के लिए प्रत्येक फलक का क्षेत्रफल ज्ञात कीजिए और इनका योग कीजिए। किसी ठोस का पृष्ठीय क्षेत्रफल उसके फलकों के क्षेत्रफलों का योग होता है। और अधिक स्पष्ट करने के लिए हम प्रत्येक आकार को एक-एक करके लेते हैं।
9.4.1 घनाभ
मान लीजिए, आप एक घनाभकार डिब्बे (आकृति 9.15) को काटकर और खोलकर समतल फैला देते हैं (आकृति 9.16), हमें एक जाल (नेट) प्राप्त होता है।
प्रत्येक भुजा की विमा लिखिए। आप जानते हैं कि घनाभ में सर्वांगसम फलकों के तीन युग्म होते हैं। प्रत्येक फलक का क्षेत्रफल ज्ञात करने के लिए आप कौन-सा व्यंजक (सूत्र) उपयोग कर सकते हैं?

डिब्बे के सभी फलकों का कुल क्षेत्रफल ज्ञात कीजिए।
आकृति 9.16 हम देखते हैं कि घनाभ का कुल पृष्ठीय क्षेत्रफल = क्षेत्रफल
इसलिए कुल पृष्ठीय क्षेत्रफल
जिसमें
यदि उपर्युक्त दर्शाए गए डिब्बे की ऊँचाई, लंबाई और चौड़ाई क्रमश:
प्रयास कीजिए
निम्नलिखित घनाभों (आकृति 9.17) का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

- घनाभ की दीवारें (तल एवं शीर्ष के अतिरिक्त फलक) पार्श्व पृष्ठ क्षेत्रफल प्रदान करती हैं। उदाहरणतः जिस घनाभाकार कमरे में आप बैठे हुए हैं उस कमरे की चारदीवारों का कुल क्षेत्रफल कमरे का पाश्श्व पृष्ठीय क्षेत्रफल है (आकृति 9.18)। अतः घनाभ का पाश्र्व पृष्ठीय क्षेत्रफल

इन्हें कीजिए
(i) एक घनाभाकार डस्टर (जिसे आपके अध्यापक कक्षा में उपयोग करते हैं) के पार्श्व पृष्ठ को भूरे रंग के कागज़ की पट्टी से इस प्रकार ढकिए कि यह डस्टर के पृष्ठ के चारों ओर बिल्कुल ठीक बैठे। कागज़ को हटाइए। कागज़ का क्षेत्रफल मापिए। क्या यह डस्टर का पार्श्व पृष्ठीय क्षेत्रफल है?
(ii) अपनी कक्षा के कमरे की लंबाई, चौड़ाई और ऊँचाई मापिए और निम्नलिखित को ज्ञात कीजिए :
(a) खिड़कियों और दरवाजों के क्षेत्रफल को छोड़कर कमरे का कुल पृष्ठीय क्षेत्रफल।
(b) इस कमरे का पार्श्व पृष्ठीय क्षेत्रफल।
(c) सफेदी किए जाने वाला, कमरे का कुल क्षेत्रफल।
सोचिए, चर्चा कीजिए और लिखिए

1. क्या हम कह सकते हैं कि घनाभ का कुल पृष्ठीय क्षेत्रफल
पार्श्व पृष्ठीय क्षेत्रफल आधार का क्षेत्रफल ? 2. यदि हम किसी घनाभ (आकृति 9.19(i)) की ऊँचाई और आधार की लंबाई को परस्पर बदलकर एक दूसरा घनाभ (आकृति 9.19(ii)), प्राप्त कर लें तो क्या पाश्श्व पृष्ठीय क्षेत्रफल बदल जाएगा?
9.4 .2 घन
इन्हें कीजिए
एक वर्गांकित कागज़ पर दर्शाए गए पैटर्न को खींचिए और उसे काटिए (आकृति 9.20(i))। आप जानते हैं कि यह पैटर्न घन का जाल (नेट) है। इसे रेखाओं के अनुदिश मोड़िए (आकृति 9.20(ii)) और घन बनाने के लिए किनारों पर टेप लगाइए (आकृति 9.20(iii))

(a) इस घन की लंबाई, चौड़ाई और ऊँचाई क्या है? ध्यान दीजिए घन के सभी फलक वर्गाकार हैं। इसलिए घन की लंबाई, चौड़ाई और ऊँचाई समान होती है (आकृति 9.21(i))।
(b) प्रत्येक फलक का क्षेत्रफल लिखिए। क्या सभी फलकों के क्षेत्रफल समान हैं?

(c) इस घन का कुल पृष्ठीय क्षेत्रफल लिखिए।
(d) यदि घन की प्रत्येक भुजा
है, तो प्रत्येक फलक का क्षेत्रफल क्या होगा (आकृति 9.21(ii))। क्या हम कह सकते हैं कि भुजा वाले घन का कुल पृष्ठीय क्षेत्रफल है?
प्रयास कीजिए
घन

सोचिए, चर्चा कीजिए और लिखिए
(i) 
आकृति 9.23
(ii) न्यूनतम पृष्ठीय क्षेत्रफल का घनाभ निर्मित करने के लिए समान भुजा वाले 12 घनों को किस प्रकार व्यवस्थित करेंगे?
(iii) किसी घन के पृष्ठीय क्षेत्रफल पर पेंट करने के पश्चात् उस घन को समान विमाओं वाले 64 घनों में काटा जाता है (आकृति 9.24)। इनमें से कितने घनों का कोई भी फलक पेंट नहीं हुआ है? कितने घनों का 1 फलक पेंट हुआ है? कितने घनों के 2 फलक पेंट हुए हैं? कितने घनों के तीन फलक पेंट हुए हैं?

आकृति 9.24
9.4 .3 बेलन
जितने भी बेलन हम देखते हैं उनमें से अधिकतर लंब वृत्तीय बेलन है। उदाहरणतः एक टिन, एक गोल खंभा, ट्यूबलाइट, पानी के पाइप इत्यादि :
इन्हें कीजिए
(i) एक बेलनाकार कैन अथवा डिब्बा लीजिए और इसके आधार का ग्राफ पेपर पर बनाइए और इसे काटकर बाहर निकाल लीजिए (आकृति 9.25(i))। एक ऐसा ग्राफ पेपर लीजिए जिसकी चौड़ाई कैन की ऊँचाई के समान हो। इस पट्टी को कैन के चारों ओर इस प्रकार लपेटिए ताकि यह कैन के चारों ओर बिल्कुल ठीक बैठे (अतिरिक्त कागज़ को हटा दीजिए) (आकृति 9.25(ii)) टुकड़ों को एक दूसरे से मिलाकर टेप लगाइए (आकृति 9.25(iii)) ताकि एक बेलन बन जाए (आकृति 9.25(iv)) कैन के चारों ओर लपेटे गए कागज़ का आकार क्या है।

नि:संदेह यह आकार में आयताकार है। जब आप इस बेलन के भागों को एक दूसरे से मिलाकर टेप लगा देते हैं तो आयताकार पट्टी की लंबाई वृत्त की परिधि के समान है। वृत्ताकार आधार की त्रिज्या
(ii) हम बेलन के पृष्ठीय क्षेत्रफल के रूप में संबंध
नोट : जब तक कुछ कहा न गया हो हम

आकृति 9.26
इसलिए बेलन का पार्श्व पृष्ठीय (वक्र पृष्ठीय) क्षेत्रफल
प्रयास कीजिए
निम्नलिखित बेलनों का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए (आकृति 9.27)

सोचिए, चर्चा कीजिए और लिखिए
नोट कीजिए कि किसी बेलन का पाश्श्व पृष्ठीय (वक्र पृष्ठीय क्षेत्रफल, आधार की परिधि
बेलन की ऊँचाई के समान होता है। क्या हम घनाभ के पार्श्व पृष्ठीय क्षेत्रफल को आधार का परिमाप घनाभ की ऊँचाई के रूप में लिख सकते हैं?
उदाहरण 4 : एक मछलीघर घनाभ के आकार का है जिसके बाह्य माप

हल :
पृष्ठभाग वाले फलक का क्षेत्रफल
पीछे वाले फलक का क्षेत्रफल
वांछित क्षेत्रफल
अतः वांछित रंगीन कागज़ का क्षेत्रफल
उदाहरण 5 : एक घनाभाकार कक्ष की आंतरिक माप
हल : मान लीजिए, कमरे की लंबाई
कमरे की चौड़ाई
कमरे की चारों दीवारों का क्षेत्रफल
सफ़ेदी कराने का प्रति वर्गमीटर खर्च
इसलिए कमरे की चार दीवारों पर सफ़ेदी कराने का कुल खर्च
छत का क्षेत्रफल
छत पर सफ़ेदी कराने का कुल खर्च
सफ़ेदी कराने का कुल खर्च
उदाहरण 6: एक भवन में 24 बेलनाकार खंभे हैं। प्रत्येक खंभे की त्रिज्या 28 सेमी और ऊँचाई 4 मी है। ₹ 8 प्रति वर्ग मीटर की दर से सभी खंभे के वक्र पृष्ठीय क्षेत्रफल पर पेंट कराने का व्यय ज्ञात कीजिए।
हल : बेलनाकार खंभे की त्रिज्या,
बेलन का वक्र पृष्ठीय क्षेत्रफल
खंभे का वक्र पृष्ठीय क्षेत्रफल
ऐसे 24 खंभों का वक्र पृष्ठीय क्षेत्रफल
अतः
उदाहरण 7 : एक ऐसे बेलन की ऊँचाई ज्ञात कीजिए जिसकी त्रिज्या
हल : मान लीजिए, बेलन की ऊँचाई
अत: बेलन की ऊँचाई
प्रश्नावली 9.2
1. दो घनाभाकार डिब्बे हैं जैसा कि संलग्न आकृति में दर्शाया गया है। किस डिब्बे को बनाने के लिए कम सामग्री की आवश्यकता है?

2.
3. एक ऐसे घन की भुजा ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल
4. रूखसार ने

5. डैनियल एक ऐसे घनाभाकार कमरे की दीवारों और छत को पेंट कर रहा है जिसकी लंबाई, चौड़ाई और ऊँचाई
क्रमश:
6. वर्णन कीजिए कि दाईं तरफ दी गई आकृतियाँ किस प्रकार एक समान हैं और किस प्रकार एक दूसरे से भिन्न हैं? किस डिब्बे का पाश्र्व पृष्ठीय क्षेत्रफल अधिक है?

7.
8. एक खोखले बेलन का वक्र पृष्ठीय क्षेत्रफल
9. किसी सड़क को समतल करने के लिए एक सड़क रोलर को सड़क के ऊपर एक बार घूमने के लिए 750 चक्कर लगाने
पड़ते हैं। यदि सड़क रोलर का व्यास

10. एक कंपनी अपने दूध पाउडर को ऐसे बेलनाकार बर्तनों में पैक करती है जिनका व्यास

9.5 घन, घनाभ और बेलन का आयतन
एक त्रिविमीय वस्तु द्वारा घिरी हुई जगह उसका आयतन कहलाता है। अपने आसपास की वस्तुओं के आयतन की तुलना करने का प्रयत्न कीजिए। उदाहरणतः किसी कमरे के अंदर रखी हुई अलमारी की तुलना में कमरे का आयतन अधिक है। इसी प्रकार आपके पेंसिल बक्स का आयतन इसके अंदर रखे पेन और मिटाने वाली रबर के आयतन से अधिक है। क्या आप इनमें से किसी भी वस्तु का आयतन माप सकते हैं?
स्मरण कीजिए, हम किसी क्षेत्र का क्षेत्रफल ज्ञात करने के लिए वर्ग इकाई का उपयोग करते हैं। यहाँ हम ठोस का आयतन ज्ञात करने के लिए घन इकाई का उपयोग करेंगे क्योंकि घन सबसे अधिक सुविधाजनक ठोस आकार हैं (ठीक उसी प्रकार जैसे किसी क्षेत्र का क्षेत्रफल मापने के लिए वर्ग सबसे अधि क सुविधाजनक आकार है)।

क्षेत्रफल ज्ञात करने के लिए हम क्षेत्र को वर्ग इकाइयों में विभाजित करते हैं, इसी प्रकार, किसी ठोस का आयतन ज्ञात करने के लिए हमें उस ठोस को घन इकाइयों में विभाजित करने की आवश्यकता है।
विचार कीजिए कि निम्नलिखित ठोसों में से प्रत्येक का आयतन 8 घन इकाई है (आकृति 9.28)।
इस प्रकार हम कह सकते हैं कि किसी ठोस का आयतन मापने के लिए हम उसमें स्थित घन इकाइयों को गिनते हैं।
अब हम घनाभ, घन और बेलन का आयतन ज्ञात करने के लिए कुछ व्यंजक (सूत्र) ज्ञात करते हैं। आइए, प्रत्येक ठोस पर एक-एक करके चर्चा करते हैं।
9.5.1 घनाभ
समान आकार (प्रत्येक घन की लंबाई समान) वाले 36 घन लीजिए एक घनाभ बनाने के लिए उन्हें व्यवस्थित कीजिए। आप इन्हें अनेक रूपों में व्यवस्थित कर सकते हैं। निम्नलिखित सारणी पर विचार कीजिए और रिक्त स्थानों की पूर्ति कीजिए :

आप क्या देखते करते हैं?
क्योंकि इन घनाभों को बनाने के लिए हमने 36 घनों का उपयोग किया है इसलिए प्रत्येक घनाभ का आयतन 36 घन इकाई है। इसके अतिरिक्त प्रत्येक घनाभ का आयतन उसकी लंबाई, चौड़ाई और ऊँचाई के गुणनफल के समान है। उपर्युक्त उदाहरण से हम कह सकते हैं कि घनाभ का आयतन

इन्हें कीजिए
एक कागज़ की शीट लीजिए और इसके क्षेत्रफल को मापिए। इसी के समान आकार वाली कागज़ की शीटों का ढेर लगाकर एक घनाभ बनाइए (आकृति 9.29)। इस ढेर की ऊँचाई मापिए। शीट के क्षेत्रफल और शीटों की ऊँचाई का गुणनफल ज्ञात करते हुए घनाभ का आयतन ज्ञात कीजिए।
यह क्रियाकलाप इस विचार को दर्शाता है कि ठोस के आयतन का निगमन इस विधि से भी किया जा सकता है (यदि किसी ठोस का आधार और शीर्ष सर्वांगसम हैं और एक दूसरे के समांतर हैं और इसके किनारे आधार पर लंब हैं) क्या आप ऐसी वस्तुओं के बारे में सोच सकते हैं जिनका आयतन इस विधि का उपयोग करते हुए ज्ञात किया जा सकता है?
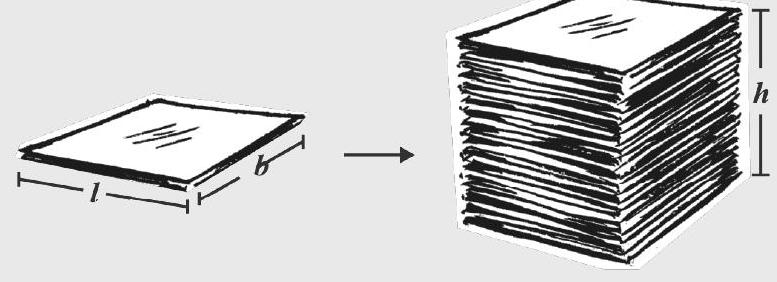
आकृति 9.29
प्रयास कीजिए
निम्नलिखित घनाभों (आकृति 9.30) का आयतन ज्ञात कीजिए :
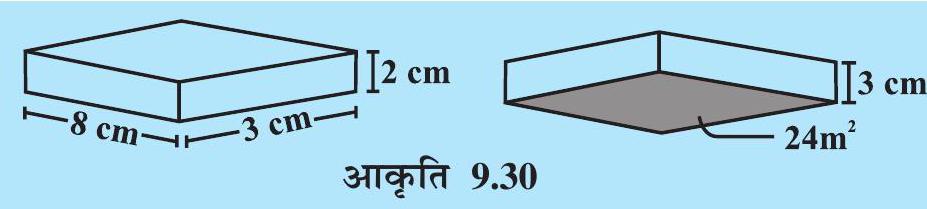
9.5.2 घन
घन, घनाभ का एक अनोखा (विशेष) उदाहरण है जिसमें
प्रयास कीजिए
निम्नलिखित घनों का आयतन ज्ञात कीजिए :
(a)
भुजा वाला (b)
भुजा वाला
इन्हें कीजिए
समान आकार वाले 64 घनों को जितने रूपों में आप व्यवस्थित कर सकते हैं उतने रूपों में व्यवस्थित करते हुए घनाभ बनाइए। प्रत्येक रूप का पृष्ठीय क्षेत्रफल ज्ञात कीजिए। क्या समान आयतन वाली ठोस आकृतियों का पृष्ठीय क्षेत्रफल समान होता है?
सोचिए, चर्चा कीजिए और लिखिए
एक कंपनी बिस्कुट बेचती है। बिस्कुटों को पैक करने के लिए घनाभाकार डिब्बों का उपयोग किया जा रहा है। डिब्बा
, डिब्बा डिब्बे का कौन सा आकार कंपनी के लिए आर्थिक दृष्टि से लाभदायक रहेगा? क्यों? क्या आप ऐसे किसी और आकार (विमाएँ) के डिब्बे का सुझाव दे सकते हैं जिसका आयतन इनके समान हो परंतु इनकी तुलना में आर्थिक दृष्टि से अधिक लाभदायक हो।
9.5.3 बेलन
हम जानते हैं कि घनाभ का आयतन उसके आधार के क्षेत्रफल और ऊँचाई का गुणनफल ज्ञात करते हुए ज्ञात किया जा सकता है। क्या इसी प्रकार हम बेलन का आयतन ज्ञात कर सकते हैं?

घनाभ की तरह बेलन में भी एक आधार और शीर्ष होता है जो एक दूसरे के सर्वांगसम और समांतर होते हैं। घनाभ की तरह इसका वक्रपृष्ठ आधार पर लंब होता है। इसलिए
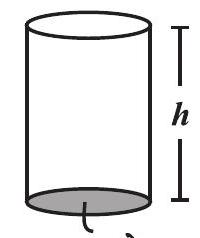
आधार का क्षेत्रफल
9.6 आयतन और धारिता
इन दो शब्दों में अधिक अंतर नहीं है।
(a) किसी वस्तु द्वारा घिरी हुई जगह की मात्रा उसका आयतन कहलाता है।
(b) किसी बर्तन में भरी गई वस्तु की मात्रा उसकी धारिता कहलाती है।
नोट : यदि किसी पानी रखे जाने वाले टिन के बर्तन में
धारिता को लीटरों में भी मापा जाता है। लीटर और
प्रयास कीजिए
संलग्न बेलनों का आयतन ज्ञात कीजिए :

उदाहरण 8: एक ऐसे घनाभ की ऊँचाई ज्ञात कीजिए जिसका आयतन
हल :
घनाभ का आयतन
अतः घनाभ की ऊँचाई
इस प्रकार घनाभ की ऊँचाई
उदाहरण 9 : एक घनाभाकार गोदाम, जिसकी माप
हल :
एक डिब्बे का आयतन
गोदाम का आयतन
गोदाम के अंदर रखे जा सकने वाले डिब्बों की संख्या
इस प्रकार गोदाम के अंदर रखे जा सकने वाले डिब्बों की संख्या 90,000 है।
उदाहरण 10:
हल : कागज़ का चौड़ाई के अनुदिश मोड़कर बेलन का निर्माण किया गया है, इसलिए कागज़ की चौड़ाई बेलन की ऊँचाई होगी और बेलन की त्रिज्या
बेलन का आयतन
अतः बेलन का आयतन

उदाहरण 11:
हल : कागज़ की लंबाई बेलन के आधार की परिधि बन जाती है और चौड़ाई, ऊँचाई बन जाती है। मान लीजिए बेलन की त्रिज्या
अथवा
इसलिए
अतः बेलन का आयतन
प्रश्नावली 9.3
1. आपको एक बेलनाकार टैंक दिया हुआ है, निम्नलिखित में से किस स्थिति में आप उसका पृष्ठीय क्षेत्रफल ज्ञात करेंगे और किस स्थिति में आयतन :
(a) यह ज्ञात करने के लिए कि इसमें कितना पानी रखा जा सकता है।
(b) इसका प्लास्टर करने के लिए वांछित सीमेंट बोरियों की संख्या।
(c) इसमें भरे पानी से भरे जाने वाले छोटे टैंकों की संख्या।
2. बेलन

3. एक ऐसे घनाभ की ऊँचाई ज्ञात कीजिए जिसके आधार का क्षेत्रफल
4. एक घनाभ की विमाएँ
5. एक ऐसे बेलन की ऊँचाई ज्ञात कीजिए जिसका आयतन
6. एक दूध का टैंक बेलन के आकार का है जिसकी त्रिज्या
7. यदि किसी घन के प्रत्येक किनारे को दुगुना कर दिया जाए, तो
(i) इसके पृष्ठीय क्षेत्रफल में कितने गुना वृद्धि होगी?
(ii) इसके आयतन में कितने गुना वृद्धि होगी?
8. एक कुंड के अंदर 60 लीटर प्रति मिनट की दर से पानी गिर रहा है। यदि कुंड का आयतन

हमने क्या चर्चा की ?
1. एक ठोस का पृष्ठीय क्षेत्रफल इसके फलकों के क्षेत्रफलों के योग के समान होता है।
2. घनाभ का पृष्ठीय क्षेत्रफल
घन का पृष्ठीय क्षेत्रफल
बेलन का पृष्ठीय क्षेत्रफल

3. किसी ठोस द्वारा घिरी हुई जगह की मात्रा इसका आयतन कहलाती है।
4. घनाभ का आयतन
घन का आयतन
बेलन का आयतन

5. (i)
(ii)
(iii)











