अध्याय 09 गति एवं समय
कक्षा 6 में आपने विभिन्न प्रकार की गतियों के बारे में पढ़ा था। आपने यह पढ़ा था कि किसी वस्तु की गति किसी सरल रेखा के अनुदिश, वर्तुल (वृत्ताकार) अथवा आवर्ती हो सकती है। क्या आपको ये तीन प्रकार की गतियाँ याद हैं?
सारणी 9.1 में गतियों के कुछ सामान्य उदाहरण दिए गए हैं। प्रत्येक उदाहरण में गति का प्रकार पहचानिए।
सारणी 9.1 विभिन्न प्रकार की गतियों के कुछ उदाहरण
| गति का उदाहरण | गति का प्रकार (सरल रेखा के अनुदिश/ वर्तुल/आवर्ती) |
|---|---|
| मार्च पास्ट करते सैनिक | |
| सीधी सड़क पर चलती बैलगाड़ी |
|
| दौड़ते धावक के हाथों की गति |
|
| चलती साइकिल के पेडल की गति |
|
| सूर्य के चारों ओर पृथ्वी की गति |
|
| झूले की गति | |
| लोलक की गति |
यह हमारा सामान्य अनुभव है कि कुछ वस्तुओं की गति मंद होती हैं, जबकि कुछ अन्य वस्तुओं की गति तीव्र होती है।
9.1 मंद अथवा तीव्र
हम जानते हैं कि कुछ वाहन अन्य वाहनों की तुलना में अधिक तीव्र गति करते हैं। यहाँ तक कि एक ही वाहन विभिन्न समयों पर तीव्र अथवा मंद गति करता है। सरलरेखीय पथ के अनुदिश गति करने वाली दस वस्तुओं की सूची बनाइए। इन वस्तुओं की गति को दो वर्गों-मंद तथा तीव्र-में बाँटिए। आपने यह कैसे निश्चित किया कि कौन-सी वस्तु मंद गति कर रही है और कौन-सी तीव्र गति कर रही है?
यदि किसी सड़क पर कई वाहन एक ही दिशा में गति कर रहे हैं, तो हम यह सरलता से बता सकते हैं कि उनमें से कौन-सा वाहन अन्य की तुलना में तीव्र गति कर रहा है। आइए हम सड़क पर चलने वाले वाहनों की गति को देखते है।
क्रियाकलाप (9.1)
चित्र 9.1 को देखिए। इसमें किसी क्षण पर सड़क पर एक ही दिशा में गति करते कुछ वाहनों की स्थिति दर्शायी गयी हैं। अब चित्र 9.2 देखिए। इसमें उन्हों वाहनों की कुछ समय पश्चात् की स्थिति दर्शायी गयी हैं। दोनों चित्रों के प्रेक्षणों के आधार पर निम्नलिखित प्रश्नों के उत्तर दीजिए।
कौन-सा वाहन सबसे तीव्र गति कर रहा है? इनमें सबसे मंद गति कौन कर रहा है?
कौन मंद अथवा तीव्र गति करता है? इसका निर्णय करने में वस्तुओं द्वारा किसी दिए गए काल-अंतराल में चली गई दूरी हमारी सहायता कर सकती है। उदाहरण के लिए, कल्पना कीजिए, आप अपने मित्र को विदा करने बस अड्डे जा रहे हैं। मान लीजिए आप बस के चलते ही अपनी साइकिल के
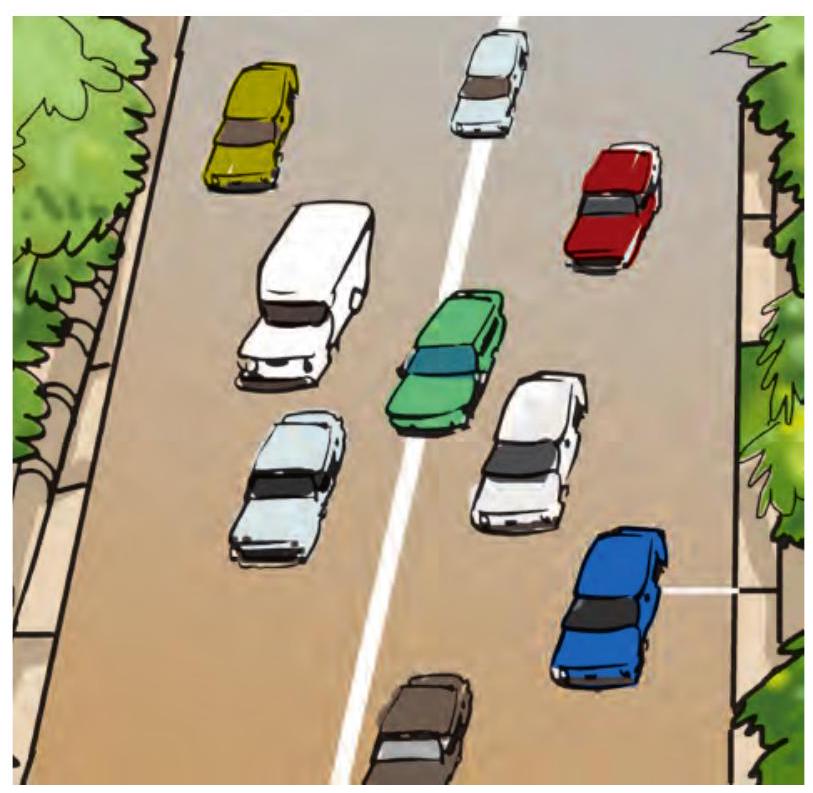
चित्र 9.1 सड़क पर एक ही दिशा में गति करते वाहन
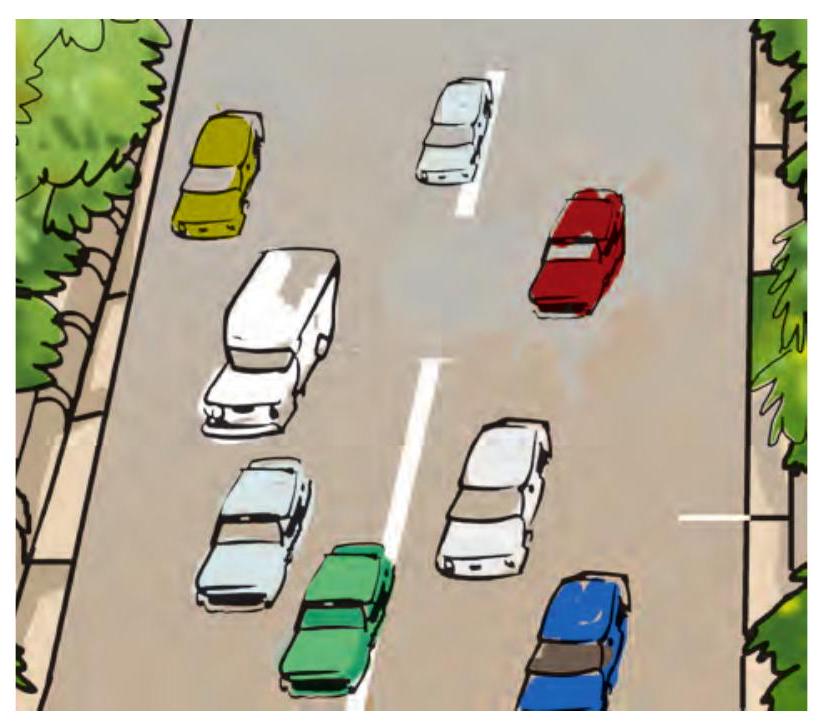
चित्र 9.2 चित्र 9.1 में दर्शाए गए वाहनों की कुछ समय पश्चात् की स्थिति
पैडल मारने लगते हैं। 5 मिनट के पश्चात् आपके द्वारा चली गई दूरी, बस द्वारा चली गई दूरी से काफ़ी कम होगी। क्या आप तब यह कहेंगे कि बस साइकिल से तीव्र गति कर रही है?
हम प्रायः यह कहते हैं कि तीव्र चलने वाले वाहनों की चाल अधिक होती है। 100 मीटर दौड़ में यह निर्णय करना सरल होता है कि किसकी चाल अधिकतम है। जो धावक 100 मीटर दूरी तय करने में सबसे कम समय लेता है, उसकी चाल अधिकतम होती है।
9.2 चाल
आप कदाचित् चाल शब्द से परिचित हैं। ऊपर दिए गए उदाहरण में अधिक चाल से यह संकेत मिलता है कि किसी दी गई दूरी को कम समय में तय किया गया है अथवा किसी दिए गए समय में अधिक दूरी तय की गई है।
दो या अधिक वस्तुओं में कौन तीव्रतम गति कर रहा है, इसे ज्ञात करने की सबसे सुविधाजनक विधि यह है कि हम इनके द्वारा किसी एकांक समय में तय की गई दूरी ज्ञात करें। इस प्रकार, यदि हम दो बसों द्वारा एक घंटे में तय की गई दूरी जानते हैं, तब हम यह बता सकते हैं कि उनमें से कौन अपेक्षाकृत मंद है। किसी वस्तु द्वारा एकांक समय में तय की गई दूरी को हम उस वस्तु की चाल कहते हैं।
जब हम यह कहते हैं कि कोई कार 50 किलोमीटर प्रति घंटा की चाल से गति करती है, तो इससे यह ज्ञात होता है कि वह कार एक घंटे में 50 किलोमीटर दूरी तय करेगी। तथापि, कोई कार बिरले ही एक घंटे तक किसी नियत चाल (समान गति) से चलती है। वास्तव में, वह धीमी चाल से गति आरंभ करके फिर अपनी चाल बढ़ाती है। अतः, जब हम यह कहते हैं कि किसी कार की चाल 50 किलोमीटर प्रति घंटा है, तो प्रायः हम केवल कार द्वारा एक घंटे में तय की गई दूरी पर ही विचार करते हैं। हम इसकी चिंता नहीं करते कि इस एक घंटे की अवधि में कार नियत चाल से चलती रही अथवा नहीं। वास्तव में, यहाँ परिकलित की गई चाल, कार की औसत चाल है। इस पुस्तक में हम औसत चाल के लिए, चाल शब्द का ही उपयोग करेंगे। अतः हम ‘तय की गई कुल दूरी’ को ‘लिए गए कुल समय’ से विभाजित करके चाल प्राप्त करते हैं। इस प्रकार
$ \text { चाल }=\frac{\text { तय की गई कुल दूरी }}{\text { लिया गया कुल समय }} $
अपने दैनिक जीवन में हम बिरले ही लंबी दूरियों तक अथवा अधिक समय तक वस्तुओं को एक नियत चाल से गति करते हुए देखते हैं। यदि किसी सरल रेखा के अनुदिश गति करने वाली वस्तु की चाल परिवर्तित होती रहती है, तो उस वस्तु की चाल असमान कही जाती है। इसके विपरीत किसी सरल रेखा के अनुदिश वस्तु की नियत चाल से गति एकसमान गति कहलाती है। इस स्थिति में औसत चाल वही है, जो वास्तविक चाल है।
यदि हम किसी वस्तु द्वारा किसी निश्चित दूरी को तय करने में लगे समय को माप लें, तो हम उस वस्तु की चाल ज्ञात कर सकते हैं। कक्षा 6 में आपने दूरी मापना सीखा था। परंतु, हम समय कैसे मापते हैं। आइए, पता लगाएँ।
9.3 समय की माप
यदि आपके पास घड़ी नहीं है, तो आप यह कैसे निश्चित करेंगे की अब क्या समय हो गया है? क्या कभी आपको यह जानने की उत्सुकता हुई है कि हमारे बुजुर्ग किस प्रकार केवल छाया देखकर दिन के समय का अनुमान लगा लेते थे?
हम एक माह के काल-अंतराल को कैसे मापते हैं? हम एक वर्ष के काल-अंतराल को कैसे मापते हैं?
समय की माप से हमारा तात्पर्य काल-अंतराल की माप से है। बोलचाल में जब हम समय मापने के लिए किसी घड़ी के उपयोग के बारे में चर्चा करते हैं, तब हमारा अभिप्राय काल-अंतराल का मापन ही होता है।
हमारे पूर्वजों ने यह देखा कि प्रकृति में बहुत-सी घटनाएँ, निश्चित अंतरालों के पश्चात् स्वयं दोहराती हैं। उदाहरण के लिए, उन्होंने यह पाया कि सूर्य प्रतिदिन प्रातः उदय होता है। एक सूर्योदय से अगले सूर्योदय के बीच के समय को एक दिन कहा गया। इसी प्रकार, एक अमावस्या (नवचंद्र) से अगली अमावस्या के बीच के समय की माप, माह के रूप में की गयी। एक वर्ष उस समय के लिए नियत किया गया, जितने समय में पृथ्वी, सूर्य की एक परिक्रमा पूरी करती है।
प्राय: हमें एक दिन से काफ़ी छोटे समय-अंतरालों को मापने की भी आवश्यकता पड़ती है। संभवतः समय मापने की सबसे सामान्य युक्ति घड़ियाँ ही है (चित्र 9.3)। क्या आपको कभी यह जानने की उत्सुकता हुई है कि घड़ियाँ समय कैसे मापती हैं?
घड़ियों की कार्यविधि काफ़ी जटिल होती है, परंतु सभी घड़ियों में आवर्ती गति का उपयोग किया जाता है। आवर्ती गति का एक चिरपरिचित उदाहरण सरल लोलक है।

चित्रण 9.3 कुछ सामान्य घड़ियाँ
सरल लोलक धातु के छोटे गोले अथवा पत्थर के टुकड़े को किसी दृढ़ स्टैण्ड से धागे द्वारा निलंबित करके बनाया जा सकता है [चित्र 9.4 (a)]। धातु के गोले को लोलक का गोलक कहते हैं।
चित्र [9.4 (a)] में लोलक को अपनी माध्य स्थिति पर विराम अवस्था में दर्शाया गया है। जब लोलक के गोले को धीरे से एक ओर ले जाकर मुक्त करते हैं, तो यह इधर-उधर गति करना आरंभ कर देता है [चित्र 9.4 (b)]। सरल लोलक की यह गति आवर्ती अथवा दोलन गति का एक उदाहरण है।
जब लोलक का गोलक अपनी माध्य स्थिति $O$ से आरंभ करके $\mathrm{A}$ तक, फिर $\mathrm{A}$ से $\mathrm{B}$ एवं $\mathrm{B}$ से वापस $\mathrm{O}$ पर आता है, तो यह कहा जाता है कि लोलक ने एक दोलन पूरा कर लिया है। लोलक तब भी एक दोलन पूरा करता है, जब इसका गोलक एक चरम स्थिति $\mathrm{A}$ से दूसरी चरम स्थिति $\mathrm{B}$ पर तथा $\mathrm{B}$ से वापस $\mathrm{A}$ पर आ जाता है। सरल लोलक एक दोलन पूरा करने में जितना समय लगाता है, उसे सरल लोलक का आवर्तकाल कहते हैं।
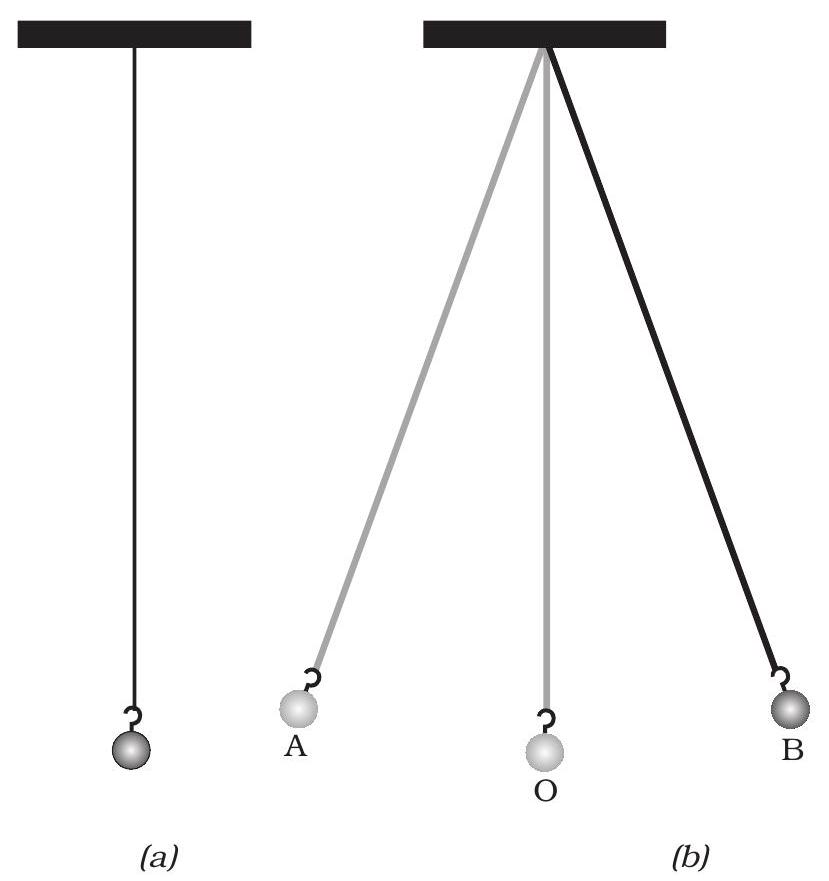
चित्र 9.4 (a) एक सरल लोलक, (b) दोलन करते सरल लोलक के गोलक की विभिन्न स्थितियाँ
क्रियाकलाप (9.2)
लगभग एक मीटर लंबा धागा अथवा डोरी लेकर चित्र 9.4 (a) में दर्शाए अनुसार एक सरल लोलक बनाइए। यदि पास में कोई पंखा चल रहा है, तो उसे बंद कीजिए। लोलक के गोलक को अपनी माध्य स्थिति पर विराम में आने दीजिए। गोलक के नीचे फ़र्श पर अथवा इसके पीछे दीवार पर उसकी माध्य स्थिति को एक चिह्न द्वारा अंकित कीजिए।
लोलक का आवर्तकाल मापने के लिए हमें विराम घड़ी की आवश्यकता होगी। यदि विराम घड़ी उपलब्ध नहीं है, तो मेज घड़ी अथवा कलाई घड़ी उपयोग की जा सकती है।
लोलक को गति में लाने के लिए, गोलक को पकड़िए और इसे धीमे से एक ओर ले जाइए। यह सुनिश्चित कीजिए कि जब आप गोलक को विस्थापित कर रहे हों, तो इससे बँधी डोरी तनी हुई हो। अब गोलक को विस्थापित स्थिति से मुक्त कीजिए। ध्यान रखिए, गोलक को छोड़ते समय इसे धक्का नहीं लगना चाहिए। जिस समय गोलक अपनी माध्य स्थिति पर है, उस समय घड़ी का समय नोट कीजिए। माध्य स्थिति की बजाय आप उस स्थिति से भी समय नोट करना आरंभ कर सकते हैं, जब गोलक अपनी किसी एक चरम स्थिति पर है। लोलक द्वारा 20 दोलन पूरा करने में लगा समय मापिए। सारणी 9.2 में अपने प्रेक्षण लिखिए। इसमें दिया गया प्रेक्षण केवल एक नमूना है। आपके प्रेक्षण इससे भिन्न हो सकते हैं। इस क्रियाकलाप को तीन-चार बार दोहराइए और अपनी प्रेक्षण सारणी में लिखिए। 20 दोलनों को पूरा करने में लगे समय को 20 से भाग देकर एक दोलन में लगा समय अर्थात् लोलक का आवर्तकाल प्राप्त कीजिए।
सारणी 9.2 सरल लोलक का आवर्तकाल डोरी की लम्बाई $=100 \mathrm{~cm}$
| 20 दोलनों के लिए लिया गया समय (s) |
आवर्तकाल (s) |
|---|---|
| 42 | 2.1 |
क्या आपके लोलक का आवर्तकाल हर बार लगभग समान आता है?
ध्यान रखिए, आरंभिक विस्थापन में थोड़ा परिवर्तन आपके लोलक के आवर्तकाल को प्रभावित नहीं करता है।
आजकल अधिकांश घड़यों में एक या दो सेलों वाले विद्युत परिपथ होते हैं। इन घड़ियों को क्वार्ट्ज घड़ी कहते हैं। इनके द्वारा मापा गया समय पहले उपलब्ध घड़ियों द्वारा मापे गए समय से अधिक यथार्थ होता है।
समय तथा चाल के मात्रक
समय का मूल मात्रक सेकंड है। इसका प्रतीक $\mathrm{s}$ है। समय के बड़े मात्रक मिनट (min) तथा घंटा (h) हैं। आप पहले ही जानते हैं कि ये मात्रक किस प्रकार एक-दूसरे से संबंधित हैं। चाल का तथाकथित मूल मात्रक क्या है? चूँकि चाल दूरी/समय है, अतः चाल का मूल मात्रक $\mathrm{m} / \mathrm{s}$ है। वास्तव में, इसे अन्य मात्रकों जैसे $\mathrm{m} / \mathrm{min}$ अथवा $\mathrm{km} / \mathrm{h}$ में भी व्यक्त किया जा सकता है।
आपको यह याद रखना चाहिए कि सभी मात्रकों के प्रतीकों को एकवचन में लिखा जाता है। उदाहरण के लिए, हम $50 \mathrm{~km}$ लिखते हैं न कि $50 \mathrm{kms}$ अथवा $8 \mathrm{~cm}$ लिखते हैं न कि $8 \mathrm{cms}$
आवश्यकता के अनुसार समय के विभिन्न मात्रकों का उपयोग किया जाता है। उदाहरण के लिए, आपकी आयु को दिनों अथवा घंटों में व्यक्त करने की अपेक्षा वर्षों में व्यक्त करना सुविधाजनक होता है। इसी प्रकार, घर से विद्यालय तक की दूरी को तय करने में लगे समय को वर्षों में व्यक्त करना बुद्धिमानी नहीं है।
एक सेकंड का काल-अंतराल कितना छोटा अथवा बड़ा होता है? जोर से “दो हज़ार एक” पुकारने में लगा समय लगभग एक सेकंड होता है। ‘दो हजार एक’ से ‘दो हजार दस’ तक ज़ोर-ज़ोर से गिनकर आप इसका सत्यापन कर सकते हैं। किसी सामान्य स्वस्थ युवा की विराम की स्थिति में नाड़ी एक मिनट में 72 बार अर्थात् 10 सेकंड में लगभग 12 बार स्पंदन करती (धड़कती) है। बच्चों में यह दर कुछ अधिक हो सकती है।
बूझो यह जानने के लिए उत्सुक है कि एक दिन में कितने सेकंड तथा एक वर्ष में कितने घंटे होते हैं। क्या आप उसकी सहायता कर सकते हैं?
इस खोज के विषय में एक रोचक कहानी है कि किसी दिए गए लोलक का आवर्तकाल नियत होता है। आपने सुप्रसिद्ध वैज्ञानिक गैलीलियो गैलीली (1564-1642 ईसवी) का नाम सुना होगा। कहा जाता है कि एक बार गैलीलियो गिरजाघर में बैठे थे। उन्होंने यह देखा कि छत से जंजीर द्वारा लटका कोई लैंप एक ओर से दूसरी ओर धीमी गति कर रहा है। उन्हें यह पाकर आश्चर्य हुआ कि लैंप के एक दोलन पूरा करने के अंतराल में उनकी नब्ज़ स्पंद (धड़कन) की संख्या हर बार समान होती है। गैलीलियो ने अपने परीक्षण को सत्यापित करने के लिए विभिन्न लोलकों के साथ प्रयोग किए। उन्होंने यह पाया कि किसी दी गई लंबाई का लोलक सदैव एक दोलन पूरा करने में समान समय लेता है। इस प्रेक्षण ने लोलकयुक्त घड़ियों के विकास को एक नई दिशा प्रदान की। कमानीयुक्त घड़ियाँ और कलाई की घड़ियाँ लोलकयुक्त घड़ियों का परिष्कृत रूप थी।

चित्र 9.5 प्राचीन काल में प्रयुक्त समय मापन की कुछ युक्तियाँ
जब लोलक वाली घड़ियाँ प्रचलित नहीं हुई थी, तब संसार के विभिन्न भागों में समय मापन के लिए बहुत-सी युक्तियों का उपयोग किया जाता था। धूपघड़ी, जल-घड़ी, रेत-घड़ी इस प्रकार की युक्तियों के कुछ उदाहरण हैं। संसार के विभिन्न भागों में इन युक्तियों के भिन्न-भिन्न डिज़ाइन बनाए गए (चित्र 9.5)।
9.4 चाल मापना
‘समय तथा दूरियाँ कैसे मापें’ यह सीखने के पश्चात् आप किसी वस्तु की चाल परिकलित कर सकते हैं।
पहेली यह जानने के लिए उत्सुक है कि जब लोलक वाली घड़ियाँ नहीं थी, तब समय कैसे मापा जाता था?
आइए, फ़र्श के अनुदिश गतिमान किसी गेंद की चाल ज्ञात करें।
क्रियाकलाप 9.3
चाक के चूर्ण अथवा चूने से फ़र्श पर एक सरल रेखा खींचिए तथा अपने मित्र से कहिए कि वह इस रेखा से एक से दो मीटर दूर खड़ा हो। अब मित्र से कहिए कि वह फ़र्श के अनुदिश इस सरल रेखा के लंबवत् किसी गेंद को धीरे से लुढ़काए। जिस क्षण गेंद सरल रेखा को पार करती है तथा जिस क्षण वह विराम में आती है, दोनों बार समय नोट कीजिए (चित्र 9.6)। गेंद विराम में आने में कितना समय लेती है? जिस बिंदु पर गेंद रेखा को पार करती है तथा जिस बिंदु पर वह विराम में आती है, इन दोनों बिंदुओं के बीच की दूरी मापिए। इसे मापने के लिए आप किसी पैमाने अथवा मापक फीते का उपयोग कर सकते हैं। इस क्रियाकलाप को विभिन्न समूह बारी-बारी से दोहराएँ तथा सभी मापों को सारणी 9.3 में लिखिए। प्रत्येक समूह के पाठ्यांकों से गेंद की चाल परिकलित कीजिए।

चित्र 9.6 गेंद की चाल मापते हुए
क्या आप अपने चलने अथवा साइकिल चलाने की चाल की तुलना अपने मित्र की चाल से करना चाहेंगे? इसके लिए आपको अपने घर अथवा किसी अन्य बिंदु से अपने विद्यालय की दूरी जानने की आवश्यकता होगी। तब आप सभी इस दूरी को तय करने में लगे समय को मापकर एक-दूसरे की चाल परिकलित कर सकते हैं। यह जानना आपके लिए रोचक हो सकता है कि आप में से किसकी चाल सबसे अधिक है। सारणी 9.4 में कुछ जीवों की चाल $\mathrm{km} / \mathrm{h}$ में दी गयी हैं। आप स्वयं इनकी चाल को $\mathrm{m} / \mathrm{s}$ में परिकलित कर सकते हैं।
सारणी 9.3 गतिमान गेंद द्वारा चली गई दूरी तथा लिया गया समय
| समूह का नाम | गेंद द्वारा चली गई दूरी (m) | लिया गया समय (s) | चाल $=\frac{\text { तय की दूरी }}{\text { लिया गया समय }}$ |
|---|---|---|---|
उपग्रहों को पृथ्वी की कक्षा में प्रमोचित (छोड़ना) करने वाले रॉकेट प्राय: $8 \mathrm{~km} / \mathrm{s}$ तक की चाल प्राप्त कर लेते हैं। इसके विपरीत कछुआ केवल $8 \mathrm{~cm} / \mathrm{s}$ (लगभग) की चाल से चल सकता है। क्या आप यह परिकलित कर सकते हैं कि कछुए की तुलना में रॉकेट की चाल कितनी गुनी है।
यदि आपको किसी वस्तु की चाल ज्ञात हो जाए, तो आप दिए गए समय में उसके द्वारा चली गई दूरी
सामान्यतः उपलब्ध घड़ियों द्वारा मापा जा सकने वाला सबसे कम समय अंतराल एक सेकंड है। तथापि, अब ऐसी विशिष्ट घड़ियाँ उपलब्ध हैं, जो एक सेकंड से छोटे समय-अंतरालों को माप सकती हैं। इनमें से कुछ घड़ियाँ एक सेकंड के दस लाखवें भाग और यहाँ तक कि एक अरबवें भाग तक के समय अंतराल माप सकती हैं। आपने माइक्रोसेकंड तथा नैनोसेकंड जैसे शब्द सुने होंगे। एक माइक्रोसेकंड-सेकंड का दसलाखवाँ भाग होता है। एक नैनोसेकंड-सेकंड का एक अरबवाँ भाग होता है। इतने छोटे समय-अंतरालों को, जो घड़ियाँ मापती हैं, उनका उपयोग वैज्ञानिक अनुसंधानों के लिए किया जाता है। खेलों में जिन समय मापने की युक्तियों का उपयोग होता है, वे सेकंड के दसवें अथवा सौवें भाग तक के समय-अन्तराल माप सकती हैं। इसके विपरीत ऐतिहासिक घटनाओं के समयों को शताब्दियों अथवा सहस्त्राब्दियों में व्यक्त किया जाता है। तारों तथा ग्रहों की आयु को प्राय: अरबों वर्ष में व्यक्त करते हैं। क्या आप उन काल-अंतरालों के परास की कल्पना कर सकते हैं, जिनसे हमें व्यवहार करना पड़ता है?
सारणी 9.4 कुछ जंतुओं द्वारा प्राप्त की जा सकने वाली तीव्रतम चाल
| वस्तु का नाम | चाल $(\mathbf{k m} / \mathbf{h})$ | चाल (m/s) |
|---|---|---|
| बाज़ | 320 | $\frac{320 \times 10 \varnothing \varnothing}{6 \varnothing \times 6 \varnothing}$ |
| चीता | 112 | |
| ब्लू फिश | $40-46$ | |
| खरगोश | 56 | |
| गिलहरी | 11 | |
| घरेलू चूहा | 40 | |
| मानव | 0.27 | |
| भीमकाय कछुआ | 0.05 | |
| घोंघा |
ज्ञात कर सकते हैं। आपको केवल चाल को समय से गुणा ही करना होगा। इसप्रकार
चली गई दूरी = चाल समय
आप यह भी ज्ञात कर सकते हैं कि दी गई चाल से चलने वाली कोई वस्तु किसी दूरी को कितने समय में तय करेगी।
$$ \text { लिया गया समय }=\frac{\text { दूरी }}{\text { चाल }} $$
बूझो यह जानना चाहता है कि क्या कोई 2 ऐसी युक्ति है, जो चाल मापती है।
आपने स्कूटर अथवा मोटर साइकिलों पर एक मीटर लगा हुआ देखा होगा। इसी प्रकार कारों, बसों तथा अन्य वाहनों के डैशबोर्डों पर मीटर देखे जा सकते हैं। चित्र 9.7 में किसी कार का डैशबोर्ड दर्शाया गया है। ध्यान दीजिए, इनमें से किसी एक मीटर के एक कोने पर $\mathrm{km} / \mathrm{h}$ लिखा है। इसे चालमापी (स्पीडोमीटर) कहते हैं। इससे सीधे ही $\mathrm{km} / \mathrm{h}$ में चाल ज्ञात हो जाती है। इसमें एक अन्य मीटर भी होता है, जो वाहन द्वारा तय की गई दूरी मापता है। इस मीटर को पथमापी (ओडोमीटर) कहते हैं।

चित्र 9.7 कार का डैशबोर्ड
विद्यालय की पिकनिक के लिए जाते समय पहेली ने यह निश्चय किया कि वह यात्रा समाप्त होने तक हर 30 मिनट के पश्चात् बस के पथमापी का पाठ्यांक अपनी नोटबुक पर लिखेगी। इसके पश्चात् उसने अपने पाठ्यांक सारणी 9.5 में लिखे।
सारणी 9.5 यात्रा के विभिन्न समयों पर पथमापी के पाठ्यांक
| समय (AM) |
पथमापी का पाठ्यांक |
आरंभिक बिंदु से दूरी |
|---|---|---|
| $8: 00 \mathrm{AM}$ | $36540 \mathrm{~km}$ | $0 \mathrm{~km}$ |
| $8: 30 \mathrm{AM}$ | $36560 \mathrm{~km}$ | $20 \mathrm{~km}$ |
| 9:00 AM | $36580 \mathrm{~km}$ | $40 \mathrm{~km}$ |
| $9: 30 \mathrm{AM}$ | $36600 \mathrm{~km}$ | $60 \mathrm{~km}$ |
| $10: 00 \mathrm{AM}$ | $36620 \mathrm{~km}$ | $80 \mathrm{~km}$ |
क्या आप बता सकते हैं कि पिकनिक स्थल विद्यालय से कितनी दूर था? क्या आप बस की चाल परिकलित कर सकते हैं? सारणी को देखकर बूझो ने पहेली से पूछा कि क्या वह बता सकती है कि $9: 45 \mathrm{AM}$ तक उसकी बस ने कितनी दूरी तय कर ली थी। पहेली के पास इस प्रश्न का कोई उत्तर नहीं था। वे अपने शिक्षक के पास गए। शिक्षक ने उनसे कहा कि इस समस्या को हल करने का एक ढंग यह है कि हम दूरी-समय ग्राफ़ खींचें। आइए, यह पता लगाएँ कि इस प्रकार का ग्राफ़ कैसे खींचा जाता है।
9.5 दूरी-समय ग्राफ़
आपने यह देखा होगा कि समाचार पत्र, पत्रिकाएँ आदि सूचनाओं को रोचक बनाने के लिए उन्हें विभिन्न प्रकार के ग्राफ़ों के रूप में प्रस्तुत करती हैं। चित्र 9.8 में दर्शाए गए ग्राफ़ के प्रकार को स्तंभग्राफ़ कहते हैं। ग्राफ़ीय निरूपण का एक अन्य प्रकार वृत्तारेख या पाई चित्र (चित्र 9.9) है। चित्र 9.10 में दर्शाया गया ग्राफ़, रेखाग्राफ़ का उदाहरण है। दूरी-समय ग्राफ़ को सामान्यतया रेखाग्राफ़ द्वारा निरूपित किया जाता है। आइए, इस प्रकार का ग्राफ़ बनाना सीखें।
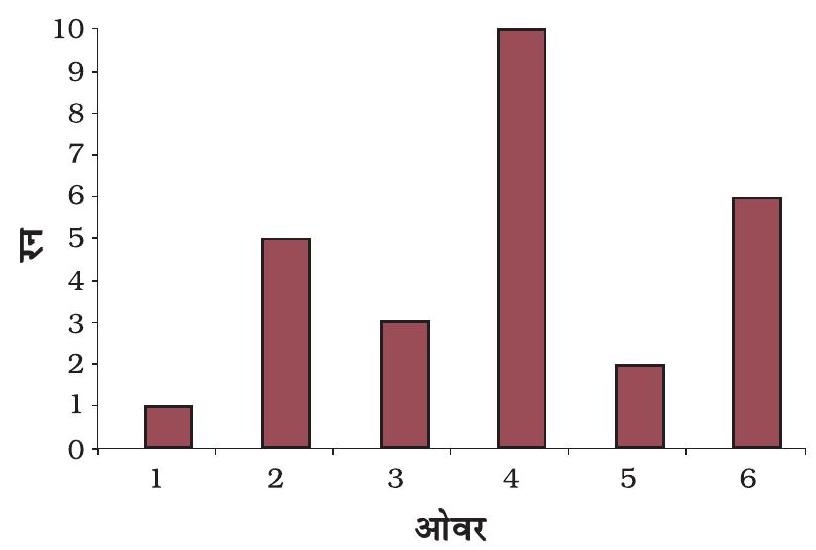
चित्र 9.8 किसी टीम द्वारा प्रत्येक ओवर में बने रनों को दर्शाता स्तंभग्राफ़
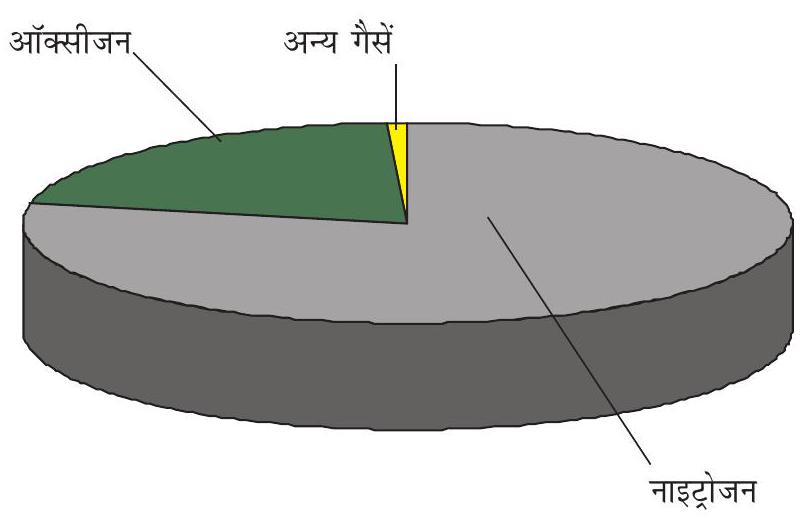
चित्र 9.9 वायु का संघटन दर्शाता वृत्तारेख
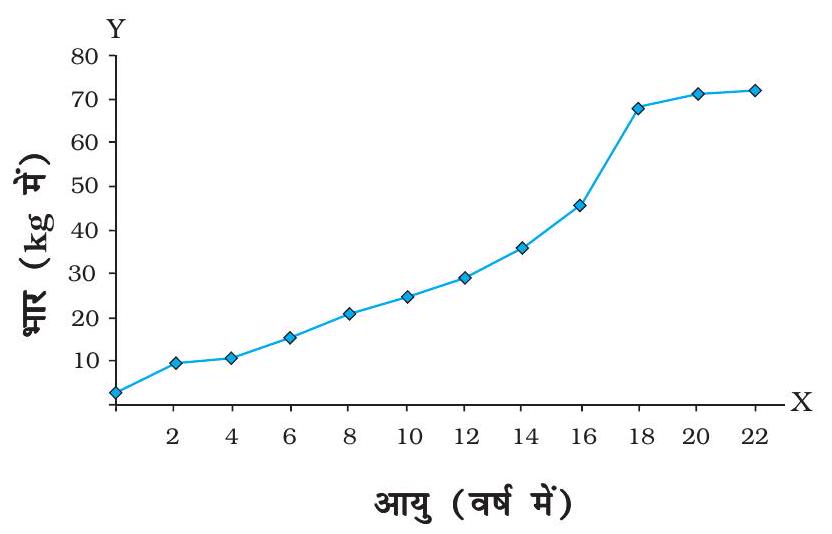
चित्र 9.10 किसी बच्चे की आयु व भार को दर्शाता रेखाग्राफ़
एक ग्राफ़ पेपर लीजिए। चित्र 9.11 में दर्शाए अनुसार इस पर एक-दूसरे के लंबवत् दो रेखाएँ खींचिए। क्षैतिज रेखा पर $\mathrm{X}^{\prime} \mathrm{OX}$ अंकित कीजिए। इसे $\mathrm{x}$-अक्ष कहते हैं। इसी प्रकार ऊर्ध्वाधर रेखा पर YOY’ अंकित कीजिए। इसे $\mathrm{y}$-अक्ष कहते हैं। $\mathrm{XOXX}^{\prime}$ तथा $\mathrm{YOY}^{\prime}$ का प्रतिच्छेद बिंदु, मूल बिंदु $O$ कहलाता है। जिन दो राशियों के बीच ग्राफ़ खींचा जाता है। उन्हें इन्हीं दो अक्षों के अनुदिश दर्शाया जाता है। हम $\mathrm{x}$-अक्ष पर धनात्मक मानों को OX के अनुदिश दर्शाते हैं। इसी प्रकार $\mathrm{y}$-अक्ष पर धनात्मक मानों को $\mathrm{OY}$ के अनुदिश दर्शाते हैं। इस अध्याय में हम केवल राशियों के धनात्मक मानों पर ही विचार करेंगे। इसलिए हम चित्र 9.11 में दर्शाए गए केवल छायांकित भाग का ही उपयोग करेंगे।
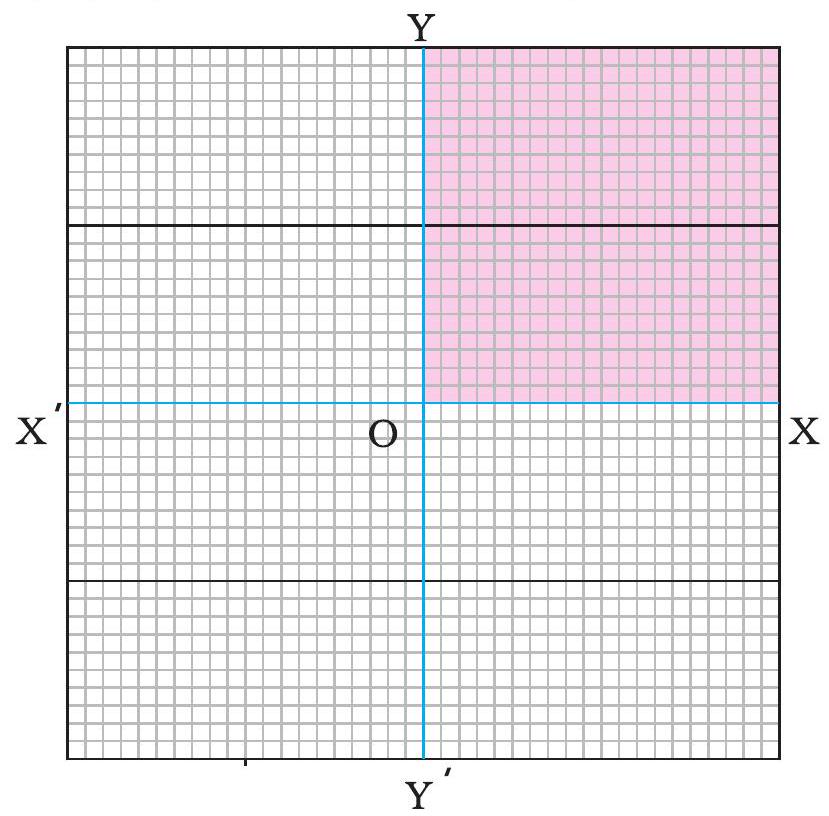
चित्र 9.11 गाफफ पेपर पर $x$-अक्ष तथा $y$-अक्ष
बूझो तथा पहेली ने किसी कार द्वारा चली गई दूरी तथा इस दूरी को तय करने में लगा समय पता लगाया। उनके आँकड़े सारणी 9.6 में दर्शाए गए हैं। सारणी 9.6 किसी कार की गति
| समय | दूरी |
|---|---|
| 0 | 0 |
| $1 \mathrm{~min}$ | $1 \mathrm{~km}$ |
| $2 \mathrm{~min}$ | $2 \mathrm{~km}$ |
| $3 \mathrm{~min}$ | $3 \mathrm{~km}$ |
| $4 \mathrm{~min}$ | $5 \mathrm{~km}$ |
| $5 \mathrm{~min}$ |
आप नीचे दिए गए चरणों को अपनाकर ग्राफ़ बना सकते हैं-
- दो अक्षों को निरूपित करने के लिए दो लंबवत् रेखाएँ खींचिए तथा चित्र 9.11 में दर्शाए अनुसार उन पर $\mathrm{OX}$ तथा $\mathrm{OY}$ अंकित कीजिए।
- यह निश्चित कीजिए कि $x$-अक्ष के अनुदिश किस राशि को दर्शाना है तथा $\mathrm{y}$-अक्ष के अनुदिश किसे दर्शाना है। $\mathrm{x}$-अक्ष के अनुदिश समय तथा $\mathrm{y}$-अक्ष के अनुदिश दूरी दर्शाइए।
- ग्राफ़ पर दूरी को निरूपित करने के लिए कोई पैमाना चुनिए तथा समय के निरूपण के लिए कोई अन्य पैमाना चुनिए। कार की गति के लिए ये पैमाने इस प्रकार हो सकते हैं:
$$ \begin{aligned} & \text { समय- } 1 \mathrm{~min}=1 \mathrm{~cm} \\ & \text { दूरी- } 1 \mathrm{~km}=1 \mathrm{~cm} \end{aligned} $$
- चुने गए पैमाने के अनुसार समय तथा दूरी के मानों को अपने-अपने अक्षों पर अंकित कीजिए। कार की गति के लिए, समय को $\mathrm{x}$-अक्ष पर मूल बिंदु से $1 \mathrm{~min}, 2 \mathrm{~min}$ द्वारा अंकित कीजिए। इसी प्रकार दूरी $1 \mathrm{~km}, 2 \mathrm{~km}$, $\mathrm{y}$-अक्ष पर अंकित कीजिए (चित्र 9.12)।
- अब आपको दूरी तथा समय के मानों के प्रत्येक समुच्चय को ग्राफ़ पेपर पर निरूपित करने के लिए उस पर बिंदु अंकित करने हैं। सारणी 9.6 के
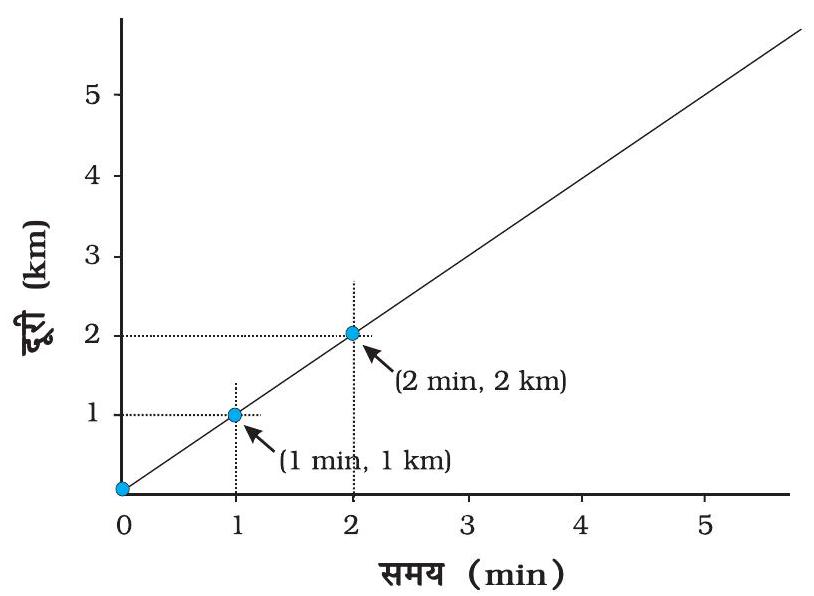
चित्र 9.12 ग्राफ़ बनाना
क्रम संख्या 1 के प्रेक्षण में यह दर्शाया गया है कि समय $0 \mathrm{~min}$ पर चली गई दूरी भी शून्य है। मानों के इस समुच्चय की ग्राफ़ पेपर पर स्थिति मूलबिंदु पर है। एक मिनट के पश्चात् कार ने एक किलोमीटर दूरी चली है। मानों के इस समुच्चय को अंकित करने के लिए $\mathrm{x}$-अक्ष पर 1 मिनट को निरूपित करने वाले बिंदु को देखिए। इस बिंदु पर $\mathrm{y}$-अक्ष के समांतर रेखा खींचिए। इसके पश्चात $\mathrm{y}$-अक्ष पर 1 $\mathrm{km}$ दूरी के संगत बिंदु से $\mathrm{x}$-अक्ष के समान्तर रेखा खींचिए। वह बिंदु, जिस पर ये दोनों रेखाएँ एक-दूसरे को काटती हैं, ग्राफ़ पेपर पर इन मानों के समुच्चय को निरूपित करता है (चित्र 9.12)। इसी प्रकार ग्राफ़ पेपर पर मानों के विभिन्न समुच्चयों के तदनुरूपी बिंदुओं को अंकित कीजिए।
- चित्र 9.12 में विभिन्न समयों पर कार की स्थितियों के सभी बिंदुओं के समुच्चयों को ग्राफ़ पर दर्शाया गया है।
- चित्र 9.12 में दर्शाए अनुसार इन बिंदुओं को मिलाइए। बिंदुओं को मिलाने पर सरल रेखा प्राप्त होती है। यह कार की गति का दूरी-समय ग्राफ़ है।
- यदि दूरी-समय ग्राफ़ एक सरल रेखा है, तो यह संकेत करता है कि वस्तु किसी नियत चाल से गति कर रही है। परंतु, यदि किसी वस्तु की चाल लगातार परिवर्तित होती है, तो ग्राफ़ की आकृति कुछ हो सकती है।
व्यापक रूप में, पैमाने का चयन इतना सरल नहीं होता, जितना चित्र 9.12 तथा चित्र 9.13 में दर्शाया गया है। हमें $\mathrm{x}$-अक्ष तथा $\mathrm{y}$-अक्ष पर वांछित राशियों को निरूपित करने के लिए दो भिन्न पैमानों का चयन करना पड़ सकता है। आइए, इस प्रक्रिया को एक उदाहरण की सहायता से समझते हैं।
आइए, फिर उसी बस की गति पर विचार करते हैं, जिसके द्वारा पहेली और उसके मित्र पिकनिक पर गए थे। बस द्वारा तय की गई दूरी तथा लिया गया समय, सारणी 9.5 में दर्शाए गए हैं। बस द्वारा तय की गई कुल दूरी $80 \mathrm{~km}$ है। यदि हम $1 \mathrm{~km}=1 \mathrm{~cm}$ पैमाना चुनने का निश्चय करें, तो हमें $80 \mathrm{~cm}$ का अक्ष खींचना होगा, जो कागज़ की शीट पर संभव नहीं है। इसके विपरीत, $10 \mathrm{~km}=1 \mathrm{~cm}$ का पैमाना चुनने पर हमें केवल $8 \mathrm{~cm}$ लंबाई के अक्ष की आवश्यकता होगी। यह पैमाना काफ़ी सुविधाजनक होगा। परंतु, यह ग्राफ़, ग्राफ़ पेपर के एक छोटे भाग को ही ढकेगा। ग्राफ़ खींचने के लिए पैमाने का चयन करते समय कुछ बातों को ध्यान में रखना चाहिए, जो इस प्रकार हैं:
- प्रत्येक राशि के अधिकतम और न्यूनतम मानों के बीच अंतर
- प्रत्येक राशि के मध्यवर्ती मान, ताकि उन मानों को ग्राफ़ पर चुने गए पैमाने के आधार पर अंकित करना सुविधाजनक हो तथा
- जिस पेपर पर ग्राफ़ खींचना है, उसके अधिकतम भाग का उपयोग करना।
मान लीजिए आपको $25 \mathrm{~cm} 25 \mathrm{~cm}$ आमाप का एक ग्राफ़ पेपर दिया गया है। ऊपर दी गई शर्तों को पूरा करने तथा सारणी 9.5 के आँकड़ों को समायोजित कर सकने के लिए एक पैमाना इस प्रकार हो सकता है:
$$ \begin{aligned} & \text { दूरी }-5 \mathrm{~km}=1 \mathrm{~cm} \text { तथा } \\ & \text { समय-6 min }=1 \mathrm{~cm} \end{aligned} $$
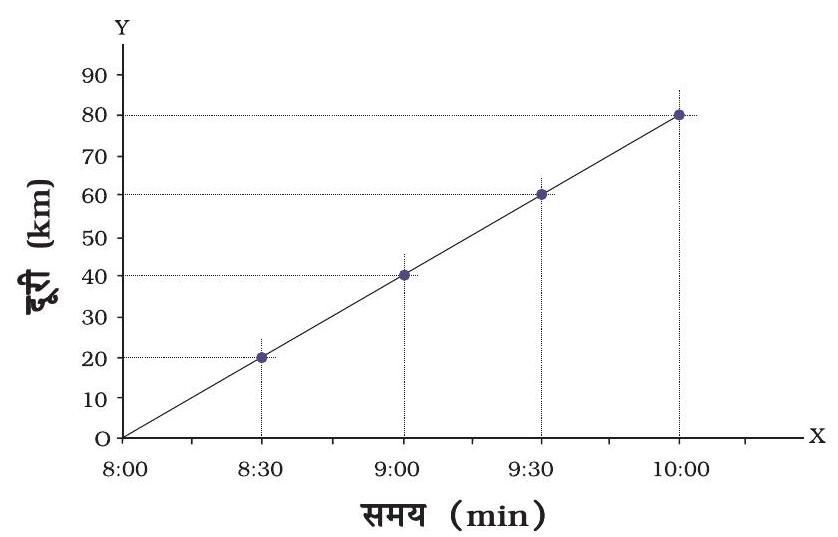
चित्र 9.13 बस की गति दर्शाता ग्राफ़
क्या अब आप बस की गति के लिए दूरी-समय ग्राफ़ खींच सकते हैं? क्या आपके द्वारा खींचा गया ग्राफ़ चित्र 9.13 में दर्शाए गए ग्राफ़ के समरूप है?
यदि सारणी द्वारा प्रस्तुत आँकड़ों से तुलना करें, तो दूरी-समय ग्राफ़ हमें गति के बारे में विविध प्रकार की जानकारी प्रदान करता है। उदाहरण के लिए, सारणी 9.5 से हमें केवल कुछ निश्चित समय अंतरालों पर ही बस द्वारा तय की गई दूरी के बारे में जानकारी मिलती है। इसके विपरीत, दूरी-समय ग्राफ़ से हम समय के किसी भी क्षण पर बस द्वारा तय की गई दूरी ज्ञात कर सकते हैं। मान लीजिए, हम 8:15 AM पर बस द्वारा चली गई दूरी ज्ञात करना चाहते हैं। इसके लिए हम $\mathrm{x}-$ अक्ष पर, उस समय ( $8: 15 \mathrm{AM}$ ) के संगत बिंदु अंकित करते हैं (चित्र 9.14)। मान लीजिए वह बिंदु $\mathrm{A}$ है। अब हम बिंदु $\mathrm{A}$ पर $\mathrm{x}$-अक्ष के लंबवत् (अथवा $\mathrm{y}$-अक्ष के समांतर) एक रेखा खींचते हैं। फिर हम ग्राफ़ के जिस बिंदु $\mathrm{T}$ पर यह लंबवत् रेखा ग्राफ़ को काटती है, उस बिंदु पर चिह्न लगाते हैं (चित्र 9.14)। इसके पश्चात् हम $\mathrm{T}$ से होकर जाने वाली $\mathrm{x}$-अक्ष के समांतर रेखा खींचते हैं। यह $\mathrm{y}$-अक्ष को बिंदु $\mathrm{B}$ पर काटती है। $\mathrm{y}$-अक्ष पर बिंदु $\mathrm{B}$ के संगत दूरी, $\mathrm{OB}$ हमें $8: 15 \mathrm{AM}$ पर बस द्वारा $\mathrm{km}$ में तय की गई दूरी प्रदान करती है। यह दूरी $\mathrm{km}$ में कितनी है? क्या आप $9: 45 \mathrm{AM}$ पर बस द्वारा तय की गई दूरी ज्ञात करने में पहेली की सहायता कर सकते हैं? क्या आप दूरी-समय ग्राफ़ से बस की चाल भी ज्ञात कर सकते हैं?
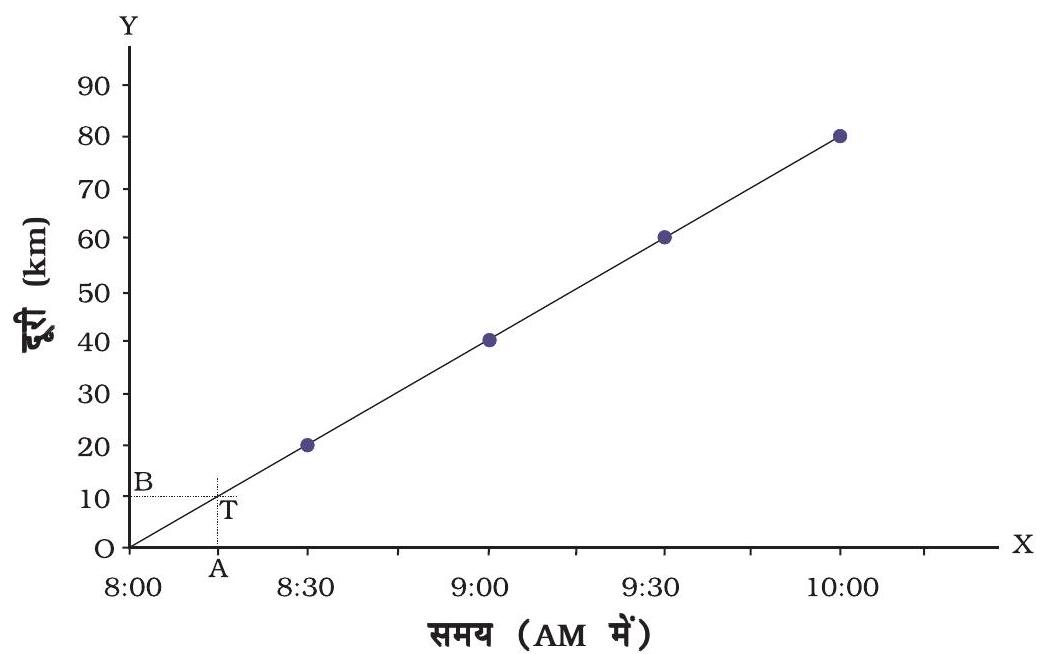
चित्र 9.14 बस को गति का दूरी-समय ग्राफ़
प्रमुख शब्द
| रेखाग्राफ़ | दोलन | आवर्तकाल |
| ग्राफ़ | सरल लोलक | एकसमान गति |
| असमान गति | चाल | समय का मात्रक |
आपने क्या सीखा
एकांक समय में किसी वस्तु द्वारा चली गयी दूरी को उसकी चाल कहते हैं। वस्तुओं की चाल यह निर्णय लेने में हमारी सहायता करती है कि कौन दूसरों से तेज चल रहा है।
किसी वस्तु की चाल उसके द्वारा तय की गई दूरी को उस दूरी को चलने में लिए गए समय से विभाजित करने पर प्राप्त होती है। इसका मूल मात्रक मीटर प्रति सेकण्ड $(\mathrm{m} / \mathrm{s})$ है।
आवर्ती घटनाओं का उपयोग समय मापन में किया जाता है। लोलक की आवर्ती गति का उपयोग घड़ियों के बनाने में होता रहा है।
वस्तुओं की गति को उनके दूरी-समय ग्राफ़ द्वारा चित्रात्मक रूप में प्रस्तुत किया जा सकता है।
नियत चाल से गति करने वाली वस्तु का दूरी-समय ग्राफ़ एक सरल रेखा होता है।
अभ्यास
1. निम्नलिखित गतियों का वर्गीकरण सरल रेखा के अनुदिश, वर्तुल तथा दोलन गति में कीजिए-
(क) दौड़ते समय आपके हाथों की गति
(ख) सीधी सड़क पर गाड़ी को खींचते घोड़े की गति
(ग) ‘मैरी गो राउंड’ झूले में बच्चे की गति
(घ) ‘सी-सॉ’ झूले पर बच्चे की गति
(च) विद्युत घंटी के हथौड़े की गति
(छ) सीधे पुल पर रेलगाड़ी की गति
2. निम्नलिखित में कौन-सा कथन सही नहीं हैं?
(क) समय का मूल मात्रक सेकंड है।
(ख) प्रत्येक वस्तु नियत चाल से गति करती है।
(ग) दो शहरों के बीच की दूरियाँ किलोमीटर में मापी जाती हैं।
(घ) किसी दिए गए लोलक का आवर्तकाल नियत नहीं होता।
(च) रेलगाड़ी की चाल $\mathrm{m} / \mathrm{h}$ में व्यक्त की जाती है।
3. कोई सरल लोलक 20 दोलन पूरे करने में $32 \mathrm{~s}$ लेता है। लोलक का आवर्तकाल क्या है?
4. दो स्टेशनों के बीच की दूरी $240 \mathrm{~km}$ है। कोई रेलगाड़ी इस दूरी को तय करने में 4 घंटे लेती है। रेलगाड़ी की चाल परिकलित कीजिए।
5. किसी कार के पथमापी का $08: 30 \mathrm{AM}$ पर पाठ्यांक $57321.0 \mathrm{~km}$ है। यदि 08:50 AM पर पथमापी का पाठ्यांक परिवर्तित होकर $57336.0 \mathrm{~km}$ हो जाता है, तो कार द्वारा चली गयी दूरी कितनी है? कार की चाल $\mathrm{km} / \mathrm{min}$ में परिकलित कीजिए। इस चाल को $\mathrm{km} / \mathrm{h}$ में भी व्यक्त कीजिए।
6. सलमा अपने घर से साइकिल पर विद्यालय पहुँचने में 15 मिनट लेती है। यदि साइकिल की चाल $2 \mathrm{~m} / \mathrm{s}$ है, तो घर से विद्यालय की दूरी परिकलित कीजिए।
7. निम्नलिखित स्थितियों में गति के दूरी-समय ग्राफ़ की आकृति दर्शाइए-
(क) नियत चाल से गति करती कार
(ख) सड़क के किनारे खड़ी कोई कार
8. निम्नलिखित में कौन-सा संबंध सही है?
(क) चाल = दूरी समय
(ख) चाल $=\frac{\text { दूरी }}{\text { समय }}$
(ग) चाल $=\frac{\text { समय }}{\text { दूरी }}$
(घ) चाल $=\frac{1}{\text { दूरी } \times \text { समय }}$
9. चाल का मूल मात्रक है-
(क) $\mathrm{km} / \mathrm{min}$
(ख) $\mathrm{m} / \mathrm{min}$
(ग) $\mathrm{km} / \mathrm{h}$
(घ) $\mathrm{m} / \mathrm{s}$
10. कोई कार $40 \mathrm{~km} / \mathrm{h}$ की चाल से 15 मिनट चलती है, इसके पश्चात् वह $60 \mathrm{~km} / \mathrm{h}$ की चाल से 15 मिनट चलती है। कार द्वारा तय की गई कुल दूरी होगी-
(क) $100 \mathrm{~km}$
(ख) $25 \mathrm{~km}$
(ग) $15 \mathrm{~km}$
(घ) $10 \mathrm{~km}$
11. मान लीजिए चित्र 9.1 तथा चित्र 9.2 में दर्शाए गए फोटोग्राफ 10 सेकंड के अंतराल पर खींचे गए। यदि इन फोटोग्राफों में 100 मीटर की दूरी को $1 \mathrm{~cm}$ द्वारा दर्शाया गया है, तो तीव्रतम कार की चाल परिकलित कीजिए।
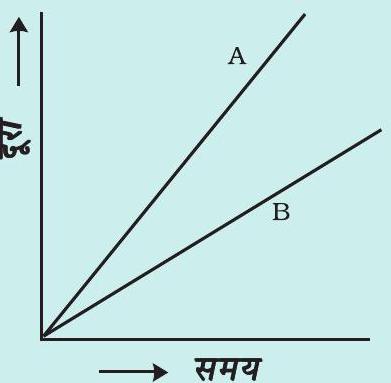
12. चित्र 9.15 में दो वाहनों, $\mathrm{A}$ तथा $\mathrm{B}$ की गति के चित्र 9.15 दो वाहनों की गति दूरी-समय ग्राफ़ दर्शाए गए हैं। इनमें से कौन-सा वाहन के दूरी-समय ग्राफ़ अपेक्षाकृत तीव्र गति से चल रहा है?
13. निम्नलिखित दूरी-समय ग्राफ़ों में से कौन उस ट्रक की गति को दर्शाता है, जिसमें उसकी चाल नियत नहीं है?

विस्तारित अधिगम - क्रियाकलाप और परियोजना कार्य
1. आप अपनी धूपघड़ी स्वयं बना सकते हैं तथा अपने स्थान पर दिन का समय अंकित करने के लिए इसे प्रयोग कर सकते हैं। सबसे पहले एटलस की सहायता से अपने शहर का अक्षांश ज्ञात कीजिए। गत्ते का त्रिभुजाकार टुकड़ा इस प्रकार काटिए कि उसका एक कोण आपके स्थान के अक्षांश के बराबर हो तथा इसका सम्मुख कोण समकोण हो। इस टुकड़े को, जिसे ‘नोमोन’ कहते हैं किसी वृत्ताकार बोर्ड पर चित्र 9.16 में दर्शाए अनुसार, उसके व्यास के अनुदिश ऊर्ध्वाधर जड़ दीजिए। नोमोन को वृत्ताकार बोर्ड में व्यास के अनुदिश खाँचा बनाकर भी जड़ा जा सकता है।
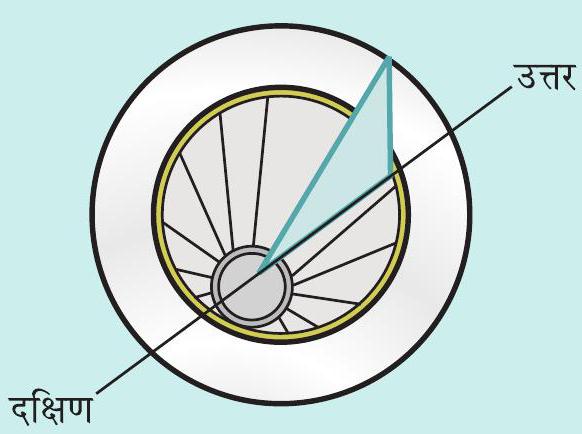
चित्र 9.16
अब कोई ऐसा खुला स्थान चुनिए, जहाँ दिन में अधिकांश समय धूप पड़ती हो। फ़र्श पर उत्तर-दक्षिण दिशा के अनुदिश एक रेखा अंकित कीजिए। चित्र 9.16 में दर्शाए अनुसार धूप में धूप घड़ी रखिए। दिन के समय जितना जल्दी संभव हो सके, मान लो 8:00 AM पर वृत्ताकार बोर्ड पर नोमोन की छाया की ‘नोक’ की स्थिति अंकित कीजिए। पूरे दिन प्रत्येक घंटे के पश्चात् ‘नोक’ की स्थिति अंकित करते रहिए। चित्र 9.16 में दर्शाए अनुसार अंकित किए गए प्रत्येक बिंदु को नोमोन के आधार के उस बिंदु से मिलाने वाली रेखाएँ खींचिए, जिस पर उस स्थान का अक्षांश कोण बना है। इन रेखाओं को वृत्ताकार बोर्ड पर उसकी परिधि तक बढ़ाइए। आप इस धूप घड़ी का उपयोग अपने स्थान पर दिन का समय ज्ञात करने के लिए कर सकते हैं। याद रखिए, चित्र 9.16 में दर्शाए अनुसार नोमोन को सदैव उत्तर-दक्षिण दिशा में ही रखना चाहिए।
2. संसार के विभिन्न भागों में प्राचीन काल में समय मापने की जो युक्तियाँ उपयोग की जाती थी उनके विषय में सूचनाएँ एकत्र कीजिए। प्रत्येक पर एक संक्षिप्त लेख लिखिए। इस लेख में युक्ति का नाम, उद्भव का स्थान, उपयोग किए जाने वाला काल, वह मात्रक, जिसमें समय मापा जाता था तथा यदि संभव हो सके, तो युक्ति का फोटोग्राफ अथवा रेखाचित्र भी सम्मिलित किया जा सकता है।
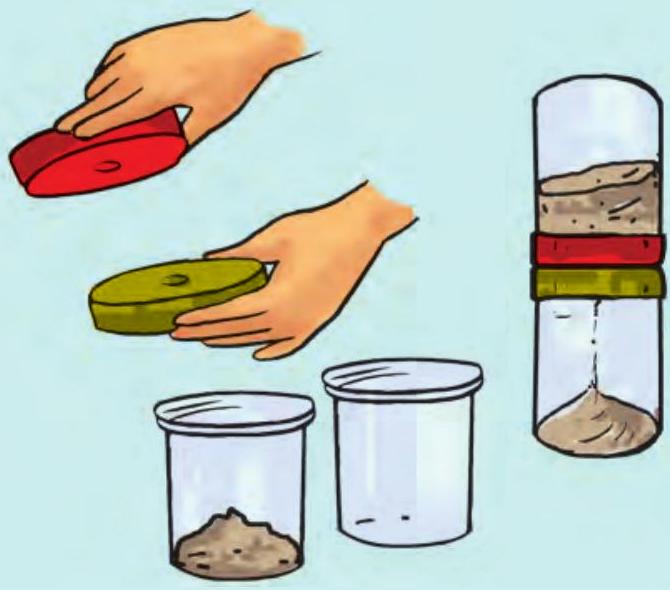
चित्र 9.17
3. 2 मिनट का समय-अंतराल माप सकने वाली रेत घड़ी का मॉडल बनाइए (चित्र 9.17)।
4. किसी पार्क में जाकर झूला झूलते समय आप एक रोचक क्रियाकलाप कर सकते हैं। इसके लिए आपको एक घड़ी चाहिए। झूले पर बिना किसी को बैठाए, उसे दोलन करने दीजिए। जिस प्रकार आपने लोलक का आवर्तकाल ज्ञात किया था, उसी प्रकार इसका आवर्तकाल ज्ञात कीजिए। यह सुनिश्चित कर लें कि झूले की गति को कोई झटका नहीं लगना चाहिए। अब अपने किसी मित्र से झूले पर बैठने के लिए कहिए। झूले को एक धक्का देकर इसे स्वाभाविक रूप से झूलने दीजिए। इसका आवर्तकाल फिर मापिए। इस क्रियाकलाप को विभिन्न व्यक्तियों को झूले पर बैठाकर दोहराइए। विभिन्न प्रकरणों में मापे गए झूले के आवर्तकालों की तुलना कीजिए। इस क्रियाकलाप से आप क्या निष्कर्ष निकालते हैं?
क्या आप जानते हैं?
भारतवर्ष में समय अनुरक्षण सेवा, नई दिल्ली की राष्ट्रीय भौतिकी प्रयोगशाला द्वारा प्रदान की जाती है। यहाँ जिन घड़ियों का उपयोग किया जाता है, वे समय-अन्तराल की माप, एक सेकंड के दस लाखवें भाग की यथार्थता के साथ कर सकती हैं। संसार की सर्वाधिक यथार्थ घड़ी संयुक्त राज्य अमेरिका (U.S.A.) के राष्ट्रीय मानक एवं प्रौद्योगिकी संस्थान द्वारा विकसित की गयी है। यह घड़ी 2 करोड़ वर्ष तक चलते रहने के पश्चात् 1 सेकंड तेज अथवा मंद होगी।










