12.1 भूमिका

सममिति (Symmetry) एक महत्वपूर्ण ज्यामितीय अवधारणा है, जो सामान्यतः प्रकृति में प्रदर्शित होती है तथा क्रियाकलाप के लगभग सभी क्षेत्रों में इसका प्रयोग होता है। कलाकार, व्यवसायी, कपड़े या ज्वैलरी डिज़ाइन करने वाले, कार निर्माता, आर्किटेक्ट तथा अनेक अन्य सममिति की संकल्पना का प्रयोग करते हैं। मधुमक्खियों के छत्तों, फूलों, पेड़ की पत्तियों, धार्मिक चिह्नों, कंबलों और रूमालों, इन सभी स्थानों पर आपको सममित डिज़ाइन दिखाई देंगे।

आर्किटेक्चर

इंजीनियरिंग

प्रकृति

आप पिछली कक्षा में, रैखिक सममिति का कुछ ‘अनुभव’ कर चुके हैं।

एक आकृति मे रैखिक सममिति होती है, यदि उसमें एक रेखा ऐसी हो जिसके अनुदिश उस आकृति को मोड़ने पर, आकृति के दोनों भाग परस्पर संपाती हो जाते हों । इन अवधारणाओं को आप याद कर सकते हैं। आपकी सहायता के लिए यहाँ कुछ क्रियाकलाप दिए जा रहे हैं।

सममिति दर्शाने वाली एक पिक्चर एलबम बनाइए

कुछ रंगीन आकर्षक इंक-डाट डेविल्स बनाइए

कागज़ के कटे हुए कुछ सममिति डिज़ाइन बनाइए

आपके द्वारा एकत्रित किए गए डिज़ाइन में सममित रेखाओं (या अक्षों) को पहचानने का आनंद लीजिए ।

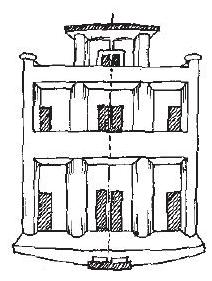
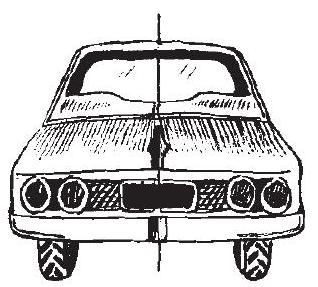
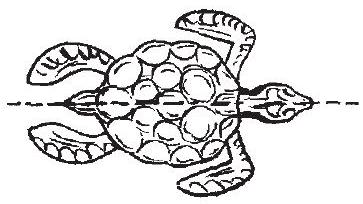
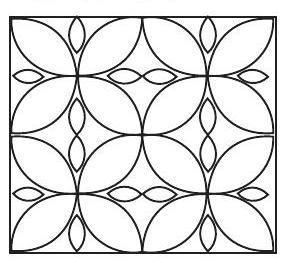
आइए अब सममिति पर अपनी अवधारणाओं को और अधिक प्रबल बनाएँ। निम्नलिखित आकृतियों का अध्ययन कीजिए, जिनमें सममित रेखाओं को बिंदुकित रेखाओं से अंकित किया गया (i) है (आकृति 12.1 (i)-(iv))।

आकृति 12.1

12.2 सम बहुभुजों के लिए सममित रेखाएँ

आप जानते हैं कि बहुभुज (polygon) एक ऐसी बंद आकृति है, जो अनेक रेखाखंडों से बनी होती है। सबसे कम रेखाखंडों से बना बहुभुज एक त्रिभुज है। (क्या आप इन रेखाखंडों से कम रेखाखंडों वाला कोई अन्य बहुभुज बना सकते हैं ? इसके बारे में सोचिए।)

एक बहुभुज, सम बहुभुज (regular polygon) कहलाता है, यदि इसकी सभी भुजाओं की लंबाइयाँ बराबर हों तथा सभी कोणों के माप बराबर हों। इस प्रकार, एक समबाहु त्रुभज, तीन भुजाओं वाला एक सम बहुभुज होता है। क्या चार भुजाओं वाला एक सम बहुभुज होता है ? क्या आप चार भुजाओं वाले एक सम बहुभुज का नाम बता सकते हैं ?

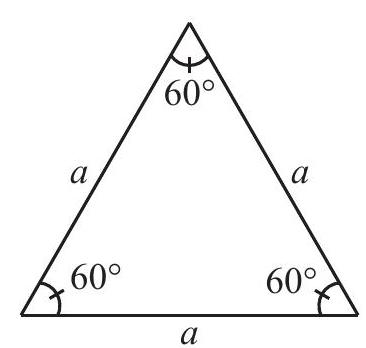
एक समबाहु त्रिभुज एक सम बहुभुज है, क्योंकि इसकी प्रत्येक भुजा की लंबाई समान होती है तथा इसके प्रत्येक कोण की माप ${60}^{\circ }$ होती है (आकृति 12.2)।

आकृति 12.2

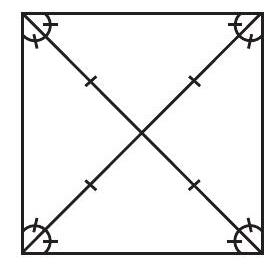
वर्ग भी एक सम बहुभुज है, क्योंकि इसकी सभी भुजाएँ समान लंबाइयों की होती हैं तथा इसका प्रत्येक कोण एक समकोण (अर्थात् ${90}^{\circ }$ ) होता है। इसके विकर्ण परस्पर समकोण पर समद्विभाजित होते हैं (आकृति 12.3)।

आकृति 12.3

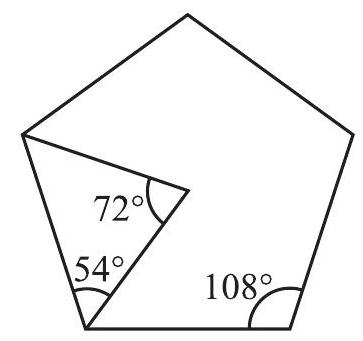
यदि एक पंचभुज (pentagon) एक सम बहुभुज है, तो स्वाभाविक है कि इसकी भुजाएँ बराबर लंबाइयों की होनी चाहिए तथा इसके कोणों के माप बराबर होने चाहिए। बाद में आप पढ़ेंगे कि इसके प्रत्येक कोण की माप ${108}^{\circ }$ होती है (आकृति 12.4)।

आकृति 12.4

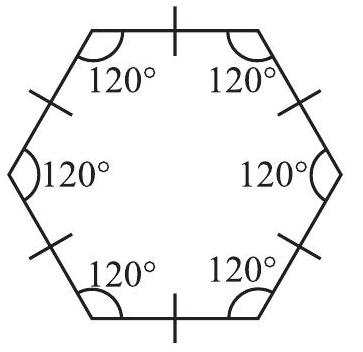
एक सम षड्भुज (regular hexagon) की सभी भुजाएँ बराबर होती हैं तथा इसके प्रत्येक कोण की माप ${120}^{\circ }$ होती है। इस आकृति के बारे में आप और अधिक बाद में पढ़ेंगे (आकृति 12.5)।

आकृति 12.5

सम बहुभुज सममित आकृतियाँ होती हैं और इसीलिए इनकी सममित रेखाएँ बहुत रोचक हैं। प्रत्येक समबहुभुज की उतनी ही सममित रेखाएँ होती हैं, जितनी उसकी भुजाएँ हैं [आकृति 12.6 (i) से (iv)]।

आकृति 12.6

संभवतः, आप कागज़ मोड़ने के क्रियाकलापों द्वारा इसकी खोज करना चाहेंगे। कोई बात नहीं, आगे बढ़िए!

रैखिक सममिति की अवधारण का दर्पण परावर्तन (mirror reflection) से निकट का संबंध है । एक आकार (shape) में रैखिक सममिति तब होती है, जब उसका एक आधा भाग दूसरे आधे भाग का दर्पण प्रतिबिंब (mirror image) हो(आकृति 12.7)। इस प्रकार एक दर्पण रेखा हमें एक सममित रेखा देखने या ज्ञात करने में सहायता करती है (आकृति 12.8)।

आकृति 12.7

आकृति 12.8

दर्पण परावर्तन के साथ कार्य करते समय, यह ध्यान रखना चाहिए कि एक आकृति के अभिमुखों (orientations) में दाएँ-बाएँ (left-right) परिवर्तन हो जाता है (आकृति 12.9)।

आकृति 12.9

छेद करने वाला यह खेल खेलिए।

आकृति 12.10

मोड़ का निशान एक सममित रेखा (या अक्ष) है। मोड़े हुए कागज़ पर विभिन्न स्थानों पर बनाए गए छेदों तथा संगत सममित रेखाओं का अध्ययन कीजिए (आकृति 12.10)।

प्रश्नावली 12.1

1. निम्नलिखित छेद की हुई आकृतियों की प्रतिलिपियाँ बनाकर (खींच कर) उनमें से प्रत्येक की सममित रेखाएँ ज्ञात कीजिए :

2. नीचे सममित रेखा (रेखाएँ) दी हुई हैं। अन्य छेद ज्ञात कीजिए।

3. निम्नलिखित आकृतियों में, दर्पण रेखा (अर्थात् सममित रेखा) बिंदुकित रेखा के रूप में दी गई है। बिंदुकित (दर्पण) रेखा में प्रत्येक आकृति का परावर्तन करके, प्रत्येक आकृति को पूरा कीजिए। (आप बिंदुकित रेखा के अनुदिश एक दर्पण रख सकते हैं और फिर प्रतिबिंब (image) के लिए दर्पण में देख सकते हैं)। क्या आपको पूरी की गई आकृति का नाम याद है ?

4. निम्नलिखित आकृतियों की एक से अधिक सममित रेखाएँ हैं। ऐसी आकृतियों के लिए यह कहा जाता है कि इनकी अनेक सममित रेखाएँ हैं।

निम्नलिखित आकृतियों में से प्रत्येक में विविध सममित रेखाओं (यदि हों तो), की पहचान कीजिए :

5. यहाँ दी हुई आकृति की प्रतिलिपि बनाइए।

किसी एक विकर्ण की सममित रेखा लीजिए तथा कुछ और वर्गों को इस तरह छायांकित कीजिए, कि यह आकृति इस विकर्ण के अनुदिश सममित हो जाए। क्या ऐसा करने की एक से अधिक विधियाँ हैं ? क्या यह आकृति दोनों विकर्णों के अनुदिश सममित होगी ?

6. निम्नलिखित आरेखों की प्रतिलिपियाँ बनाइए तथा प्रत्येक आकार को इस तरह पूरा कीजिए ताकि वह आकार दर्पण रेखा (या रेखाओं) के अनुदिश सममित हो :

7. निम्नलिखित आकृतियों के लिए सममित रेखाओं की संख्याएँ बताइए :

(a) एक समबाहु त्रिभुज

(b) एक समद्विबाहु त्रिभुज

(c) एक विषमबाहु त्रिभुज

(d) एक वर्ग

(e) एक आयत

(f) एक समचतुर्भुज

(g) एक समांतर चतुर्भुज

(h) एक चतुर्भुज

(i) एक सम षड्भुज

(j) एक वृत्त

8. अंग्रेजी वर्णमाला के किन अक्षरों में निम्नलिखित के अनुदिश परावर्तन सममिति (दर्पण परावर्तन से संबंधित सममिति) है :

(a) एक ऊर्ध्वाधर दर्पण

(b) एक क्षैतिज दर्पण

(c) ऊर्ध्वाधर और क्षैतिज दर्पण दोनों

9. ऐसे आकारों के तीन उदाहरण दीजिए, जिनमें कोई सममित रेखा न हो।

10. आप निम्नलिखित आकृतियों की सममित रेखा के लिए अन्य क्या नाम दे सकते हैं ?

(a) एक समद्विबाहु त्रिभुज

(b) एक वृत्त

12.3 घूर्णन सममिति

जब घड़ी की सुइयाँ घूमती हैं, तो आप क्या कहते हैं? आप कहते हैं कि ये घूर्णन (Rotate) कर रही हैं।

घड़ी की सुइयाँ केवल एक ही दिशा में घूमती हैं। यह घूमना एक बिंदु के चारों ओर होता है, जो घड़ी के पटल (face) का केंद्र है ।

घड़ियों की सुइयाँ जिस दिशा में घूमती हैं, वह घूर्णन (rotation) दक्षिणावर्त (clockwise) घूर्णन कहलाता है, अन्यथा घूर्णन वामावर्त (anticlockwise rotation) कहलाता है।

छत के पंखे की पँखुडियों के घूर्णन के बारे में आप क्या कह सकते हैं ? क्या ये दक्षिणावर्त दिशा में घूमती हैं या वामावर्त दिशा में घूमती हैं ? अथवा क्या ये दोनों दिशाओं में घूमती हैं ?

यदि आप साइकिल के एक पहिए को घुमाते हैं, तो वह घूर्णन करता है। यह दोनों ही दिशाओं, अर्थात् दक्षिणावर्त और वामावर्त दिशाओं में घूर्णन कर सकता है। (i) दक्षिणावर्त घूर्णन और (ii) वामावर्त घूर्णन में से प्रत्येक के लिए तीन उदाहरण दीजिए।

जब कोई वस्तु घूर्णन करती है, तो उसके आकार और माप में कोई परिवर्तन नहीं होता है। घूर्णन उस वस्तु को एक निश्चित बिंदु के चारों तरफ घुमाता है। यह निश्चित बिंदु घूर्णन का

केंद्र (centre of rotation) कहलाता है । घड़ी की सुईयों के घूर्णन का केंद्र क्या है ? इसके बारे में सोचिए।

घूर्णन के दौरान घूमे गए कोण को घूर्णन कोण (angle of rotation) कहते हैं। आप जानते हैं कि एक पूरे चक्कर में ${360}^{\circ }$ का घूर्णन होता है। (i) एक आधे या अर्ध चक्कर और (ii) एक चौथाई चक्कर के घूर्णन कोणों के क्रमशः क्या माप हैं ? एक अर्ध चक्र का अर्थ ${180}^{\circ }$ का घूर्णन है तथा एक-चौथाई चक्कर का अर्थ ${90}^{\circ }$ का घूर्णन है।

जब 12 बजते हैं, तो घड़ी की दोनों सुइयाँ एक साथ होती हैं। 3 बजने तक मिनट की सुई तो तीन पूरे चक्कर लगा लेती है, परंतु घंटे की सुई केवल एक-चौथाई चक्कर ही लगा पाती है। 6 बजे की उनकी स्थितियों के बारे में आप क्या कह सकते हैं ?

क्या आपने कभी कागज़ की हवाई चकरी (या फिरकी) (paper windmill) बनाई है ? आकृति में दिखाई गई कागज़ की हवाई चकरी सममित दिखाई देती है (आकृति 12.11), परंतु आपको इसकी कोई सममिति रेखा प्राप्त नहीं होती है। इसको किसी प्रकार से मोड़ने पर भी दोनों आधे भाग संपाती नहीं होंगे। यदि आप इसके केंद्र (बीच) वाले स्थिर (या निश्चत) बिंदु के परित ${90}^{\circ }$ के कोण पर घुमाएँ, तो आप देखेंगे की हवाई चकरी का आकार, आकृति 12.11 की स्थिति के अनुसार, पहले जैसा ही है। हम कहते हैं कि चकरी में एक घूर्णन सममिति (rotational symmetry) है ।

आकृति 12.11

एक पूरे चक्कर में, ऐसी चार स्थितियाँ हैं $({90}^{\circ },{180}^{\circ },{270}^{\circ }$ और ${360}^{\circ }$ के कोणों पर घुमाने या घूर्णन करने पर), जब चकरी पहली जैसी ही दिखती है। (आकृति 12.12)। इसी कारण, हम कहते हैं कि चकरी में क्रम 4 (order 4) की घूर्णन सममिति है।

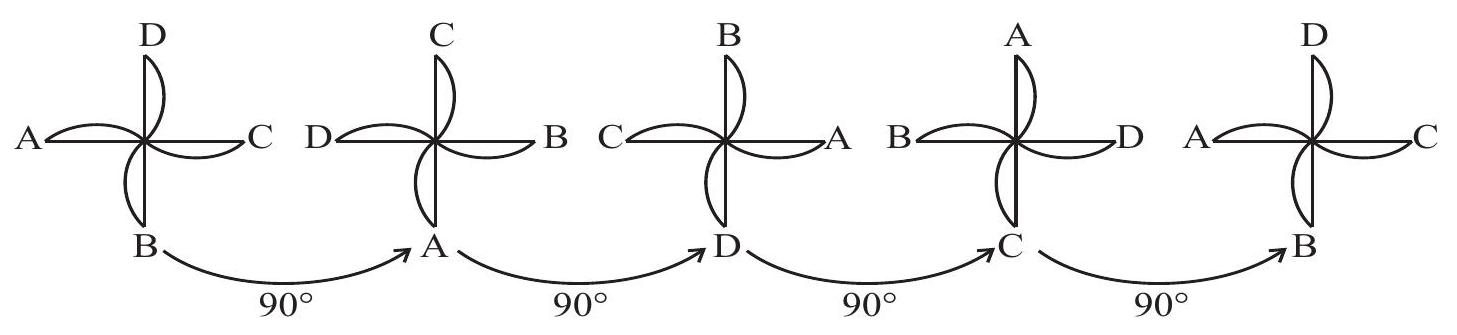
आकृति 12.12

घूर्णन सममिति का एक और उदाहरण देखिए। एक वर्ग पर विचार कीजिए, जिसका एक कोना (या शीर्ष) P है (आकृति 12.13)।

आइए इस वर्ग के केंद्र को $\times$ से अंकित करके इसके परित इस वर्ग को एक-चौथाई चक्कर पर घुमाएँ।

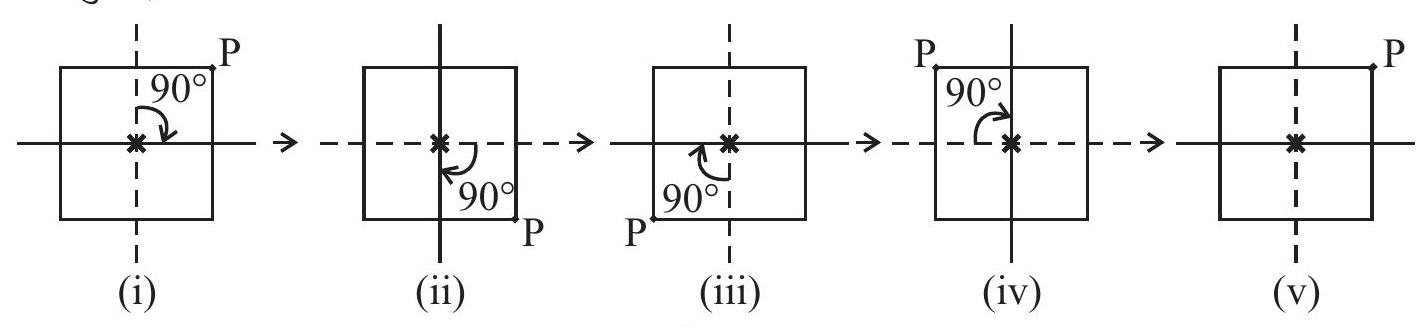
आकृति 12.13

आकृति 12.13 (i) इसकी प्रारंभिक स्थिति है । केंद्र के चारों ओर ${90}^{\circ }$ घूमाने पर आकृति 12.13 (ii) प्राप्त होती है । अब बिंदु $\mathrm{P}$ की स्थिति को देखिए। वर्ग को पुन: ${90}^{\circ }$ के कोण पर घुमाइए (घूर्णन दीजिए)। आपको आकृति 12.13(iii) प्राप्त होती है। इस प्रकार, जब आप वर्ग को चार एक-चौथाई चक्कर घुमा देते हैं, तो वह अपनी प्रारंभिक स्थिति पर आ जाती है। अब यह आकृति 12.13 (i) जैसी ही दिखती है। इसे $\mathrm{P}$ द्वारा ली गई विभिन्न स्थितियों से देखा जा सकता है।

इस प्रकार, एक वर्ग में उसके केंद्र के चारों ओर क्रम 4 की घूर्णन सममिति होती है। ध्यान दीजिए कि इस स्थिति में,

(i) घूर्णन का केंद्र वर्ग का केंद्र है ।

(ii) घूर्णन का कोण ${90}^{\circ }$ है।

(iii) घूर्णन की दिशा दक्षिणावर्त है।

(iv) घूर्णन सममिति का क्रम 4 है ।

प्रयास कीजिए

1. (a) क्या अब आप एक समबाहु त्रिभुज के लिए, घूर्णन सममिति के क्रम को बता सकते हैं (आकृति 12.14) ?

आकृति 12.14

(b) जब उपरोक्त त्रिभुज को उसके केंद्र के परित (चारों ओर) ${120}^{\circ }$ के कोण पर घुमाया जाता है, तो कितनी स्थितियों में त्रिभुज (स्थिति के अनुसार) पहले जैसा ही लगता है ?

2. निम्नलिखित में से कौन-से आकारों (आकृति 12.15) में अंकित बिंदु के परित (चारों ओर) घूर्णन सममिति है ?

आकृति 12.15

इन्हें कीजिए

दो एक जैसे (सर्वासम समांतर चतुर्भुज खींचिए, एक समांतर चतुर्भुज $\mathrm{ABCD}$ एक कागज़ पर तथा दूसरा समांतर चतुर्भुज ${\mathrm{A}}^{\prime }{\mathrm{B}}^{\prime }{\mathrm{C}}^{\prime }{\mathrm{D}}^{\prime }$ एक पारदर्शक शीट (transparent sheet) पर । उनके विकर्णों के प्रतिच्छेद बिंदुओं को क्रमशः $\mathrm{O}$ और $\mathrm{O}$ ‘से अंकित (या व्यक्त) कीजिए (आकृति 12.16) ।

समांतर चतुर्भुजों को इस प्रकार रखिए कि ${\mathrm{A}}^{\prime }$ शीर्ष $\mathrm{A}$ पर रहे, ${\mathrm{B}}^{\prime }$ शीर्ष $\mathrm{B}$ पर रहे, इत्यादि ।

इन आकारों में, अब बिंदु $\mathrm{O}$ पर एक पिन को लगाइए। अब पारदर्शक शीट को दक्षिणावर्त दिशा में घुमाइए। एक पूरे चक्कर में पारदर्शक शीट पर बना आकार कागज़ पर बने आकार से कितनी बार संपाती होता है ? इसमें घूर्णन सममिति का क्या क्रम है ?

वह बिंदु, जहाँ हमने पिन लगाई है, घूर्णन का केंद्र है। इस स्थिति में, यह विकर्णों का प्रतिच्छेद बिंदु है ।

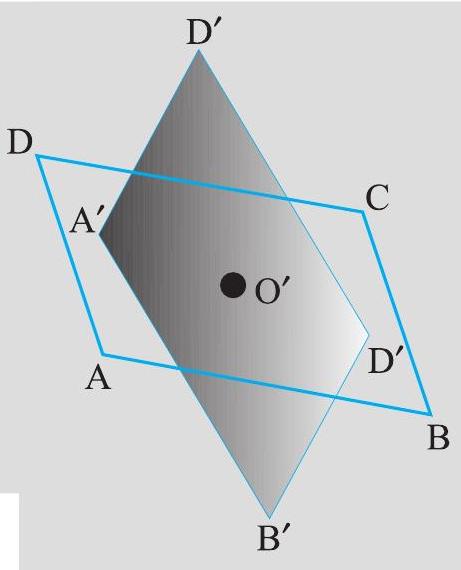
आकृति 12.17

प्रत्येक वस्तु (या आकृति) में, क्रम 1 की घूर्णन सममिति होती है, क्योंकि ${360}^{\circ }$ के घूर्णन के बाद (अर्थात् पूरे एक चक्कर के बाद) वह अपनी प्रारंभिक आकृति 12.16 स्थिति में आ जाता है। ऐसी स्थितियों में हमारी कोई रूचि नहीं होगी। आपके परिवेश में अनेक ऐसे आकार हैं जिनमें घूर्णन सममिति होती है (आकृति 12.17)।

उदाहरणार्थ, जब कुछ फलों को काटते हैं, तो उनके अनुप्रस्थ काट (cross-section) ऐसे आकारों के होते हैं, जिनमें घूर्णन सममिति होती है। जब आप इन्हें देखेंगे तो आप आश्चर्यचकित हो सकते हैं [आकृति 12.17 (i)]।

आकृति 12.17

ऐसे कई सड़क संकेत (road signs) भी हैं, जो घूर्णन सममिति प्रदर्शित करते हैं। अगली बार जब आप किसी व्यस्त सड़क पर घूमने निकलें, तो ऐसे सड़क संकेतों को पहचानिए और उनकी घूर्णन सममिति के क्रमों को ज्ञात कीजिए [आकृति 14.17(ii)]।

घूर्णन सममिति के कुछ अन्य उदाहरणों के बारे में सोचिए। प्रत्येक स्थिति में, निम्नलिखित की चर्चा कीजिए :

(i) घूर्णन का केंद्र

(ii) घूर्णन का कोण

(iii) घूर्णन किस दिशा में किया गया है

(iv) घूर्णन सममिति का क्रम

प्रयास कीजिए

दी हुई आकृतियों के लिए $\times$ से अंकित बिंदु के परित घूर्णन सममिति का क्रम बताइए (आकृति 12.18)।

प्रश्नावली 12.2

1. निम्नलिखित आकृतियों में से किन आकृतियों में 1 से अधिक क्रम की घूर्णन सममिति है?

2. प्रत्येक आकृति के घूर्णन सममिति का क्रम बताइए।

12.4 रैखिक सममिति और घूर्णन सममिति

आप अभी तक अनेक आकारों और उनकी सममितियों को देखते आ रहे हैं। अब तक आपने यह समझ लिया होगा कि कुछ आकारों में केवल रैखिक सममिति होती है, कुछ में केवल घूर्णन सममिति होती है तथा कुछ आकारों में रैखिक तथा घूर्णन दोनों प्रकार की सममितियाँ होती हैं।

उदाहरणार्थ, एक वर्ग के आकार को देखिए (आकृति 12.19)। इसकी कितनी सममित रेखाएँ हैं ? क्या इसमें कोई घूर्णन सममिति है ?

यदि उत्तर ‘हाँ’ है, तो इस घूर्णन सममिति का क्रम क्या है ? इसके बारे में सोचिए।

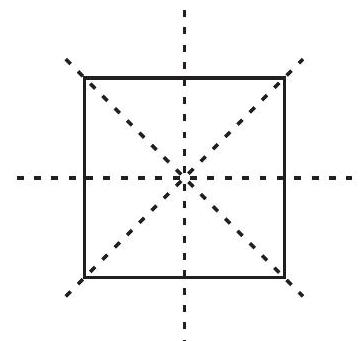
आकृति 12.19

एक वृत्त सबसे अधिक पूर्ण सममित आकृति है, क्योंकि इसको इसके केंद्र के परित किसी भी कोण पर घुमा कर वही आकृति प्राप्त की जा सकती है, अर्थात् इसमें अपरिमित रूप से अनेक क्रम की घूर्णन सममिति है तथा साथ ही इसकी अपरिमित सममित रेखाएँ हैं। वृत्त के किसी भी प्रतिरूप को देखिए। केंद्र से होकर जाने वाली प्रत्येक रेखा (अर्थात् प्रत्येक व्यास) परावर्तन सममिति की एक सममिति रेखा है तथा केंद्र के परित प्रत्येक कोण के लिए इसकी एक घूर्णन सममिति है।

इनें कीजिए

अंग्रेज़ी वर्णमाला के कुछ अक्षरों में अद्भुत एवं आकर्षक सममितीय संरचनाएँ (structures) हैं। किन बड़े अक्षरों में केवल एक ही सममित रेखा है (जैसे $\mathbf{E}$ )? किन बड़े अक्षरों में क्रम 2 की घूर्णन सममिति है (जैसे $\mathbf{I}$ )?

उपरोक्त प्रकार से सोचते हुए, आप निम्नलिखित सारणी को भरने में समर्थ हो पाएँगे:

प्रश्नावली 12.3

1. किन्हीं दो आकृतियों के नाम बताइए, जिनमें रैखिक सममिति और क्रम $1$ से अधिक की घूर्णन सममिति दोनों ही हों।

2. जहाँ संभव हो, निम्नलिखित की एक रफ़ आकृति खींचिए :

(i) एक त्रिभुज, जिसमें रैखिक सममिति और क्रम $1$ से अधिक की घूर्णन सममिति दोनों ही हों।

(ii) एक त्रिभुज, जिसमें केवल रैखिक सममिति और क्रम $1$ से अधिक की घूर्णन सममिति न हो।

(iii) एक चतुर्भुज जिसमें क्रम $1$ से अधिक की घूर्णन सममिति हो, पंरतु रैखिक सममिति न हो।

(iv) एक चतुर्भुज जिसमें केवल रैखिक सममिति हो और क्रम $1$ से अधिक की घूर्णन सममिति न हो।

3. यदि किसी आकृति की दो या अधिक सममित रेखाएँ हों, तो क्या यह आवश्यक है कि उसमें क्रम $1$ से अधिक की घूर्णन सममिति होगी ?

4. रिक्त स्थानों को भरिए :

5. ऐसे चतुर्भुजों के नाम बताइए, जिनमें रैखिक सममिति और क्रम $1$ से अधिक की घूर्णन सममिति दोनों ही हों।

6. किसी आकृति को उसके केंद्र के परित ${60}^{\circ }$ के कोण पर घुमाने पर, वह उसकी प्रारंभिक स्थिति जैसी ही दिखाई देती है। इस आकृति के लिए ऐसे कौन-से अन्य कोणों के लिए भी हो सकता है ?

7. क्या हमें कोई ऐसी क्रम $1$ से अधिक की घूर्णन सममिति प्राप्त हो सकती है, जिसके घूर्णन के कोण निम्नलिखित हों ?

(i) ${45}^{\circ }$

(ii) ${17}^{\circ }$

हमने क्या चर्चा की ?

1. एक आकृति मे रैखिक सममिति तब होती है, जब कोई ऐसी रेखा प्राप्त की जा सके जिसके अनुदिश उस आकृति को मोड़ने पर, उसके दोनों भाग परस्पर संपाती हो जाएँ।

2. सम बहुभुजों में बराबर भुजाएँ और बराबर कोण होते हैं। उनकी अनेक अर्थात् एक से अधिक, सममित रेखाएँ होती हैं।

3. प्रत्येक सम बहुभुज की उतनी ही सममित रेखाएँ होती हैं, जितनी उसकी भुजाएँ होती हैं।

4. दर्पण परावर्तन से ऐसी सममिति प्राप्त होती है, जिसमें बाएँ-दाएँ अभिमुखों का ध्यान रखना होता है ।

5. घूर्णन में एक वस्तु को एक निश्चित बिंदु के परित घुमाया जाता है। यह निश्चित बिंदु घूर्णन का केंद्र कहलाता है। जिस कोण पर वस्तु घूमती है, उसे घूर्णन का कोण कहते हैं। आधे या अर्ध चक्कर का अर्थ ${180}^{\circ }$ का घूर्णन है तथा एक-चौथाई चक्कर का अर्थ ${90}^{\circ }$ का घूर्णन है। घूर्णन दक्षिणावर्त और वामावर्त दोनों ही दिशाओं में हो सकता है।

6. यदि घूर्णन के बाद, वस्तु, स्थिति के अनुसार, पहले जैसी ही दिखाई देती है, तो हम कहते हैं कि उसमें घूर्णन सममिति है।

7. एक पूरे चक्कर ( ${360}^{\circ }$ के) में, एक वस्तु जितनी बार स्थिति के अनुसार, पहले जैसी ही दिखाई देती है, वह संख्या उस घूर्णन सममिति का क्रम कहलाती है। उदाहरणार्थ, एक वर्ग की घूर्णन सममिति का क्रम 4 है तथा एक समबाहु त्रिभुज की घूर्णन सममिति का क्रम 3 है।

8. कुछ आकारों में केवल एक ही सममिति रेखा होती है, जैसे अक्षर $\mathrm{E}$; कुछ में केवल घूर्णन सममिति ही होती है, जैसे अक्षर $\mathrm{S}$ तथा कुछ में दोनों प्रकार की सममितियाँ होती हैं, जैसे अक्षर $\mathrm{H}$ है। सममिति का अध्ययन इसलिए महत्वपूर्ण है, क्योंकि इसका दैनिक जीवन में अधिकांशतः प्रयोग होता है तथा इससे भी अधिक महत्व इस कारण है कि यह हमें सुंदर एवं आकर्षक डिज़ाइन प्रदान कर सकती है।