अध्याय 09 परिमाप और क्षेत्रफल
9.1 समांतर चतुर्भुज का क्षेत्रफल
हमें वर्ग और आयत के अतिरिक्त बहुत से दूसरे आकार देखने को मिलते हैं। आप एक भूखंड का क्षेत्रफल कैसे ज्ञात करेंगे जिसका आकार समांतर चतुर्भुज जैसा है? आइए समांतर चतुर्भुज का क्षेत्रफल प्राप्त करने की एक विधि ज्ञात करें।
क्या एक समांतर चतुर्भुज को एक समान क्षेत्रफल वाले आयत में रूपांतरित किया जा सकता है?
ग्राफ़ पेपर पर एक समांतर चतुर्भुज बनाइए जैसाकि आकृति

आकृति 9.1
आप कैसा आकार प्राप्त करते हैं? आप एक आयत प्राप्त करते हैं। क्या समांतर चतुर्भुज का क्षेत्रफल बनाए गए आयत के क्षेत्रफल के बराबर है?
हाँ, समांतर चतुर्भुज का क्षेत्रफल
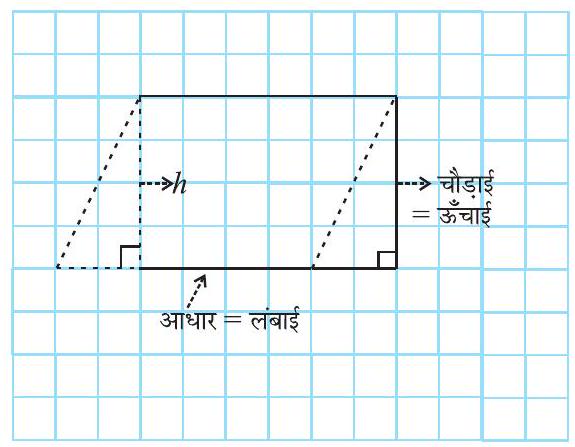
आकृति 9.2
हमने देखा कि बनाए गए आयत की लंबाई, समांतर चतुर्भुज के आधार की लंबाई के बराबर है और आयत की चौड़ाई, समांतर चतुर्भुज की ऊँचाई के बराबर है (आकृति 9.2)।
अब, समांतर चतुर्भुज का क्षेत्रफल
लेकिन आयत की लंबाई
इस प्रकार, समांतर चतुर्भुज का क्षेत्रफल
समांतर चतुर्भुज की किसी भी भुजा को आधार ले सकते हैं। इस भुजा पर, सम्मुख शीर्ष से डाला गया लंब, इसकी ऊँचाई कहलाती है। समांतर चतुर्भुज

इस समांतर चतुर्भुज

निम्न समांतर चतुर्भुजों के बारे में सोचिए (आकृति 9.3)।
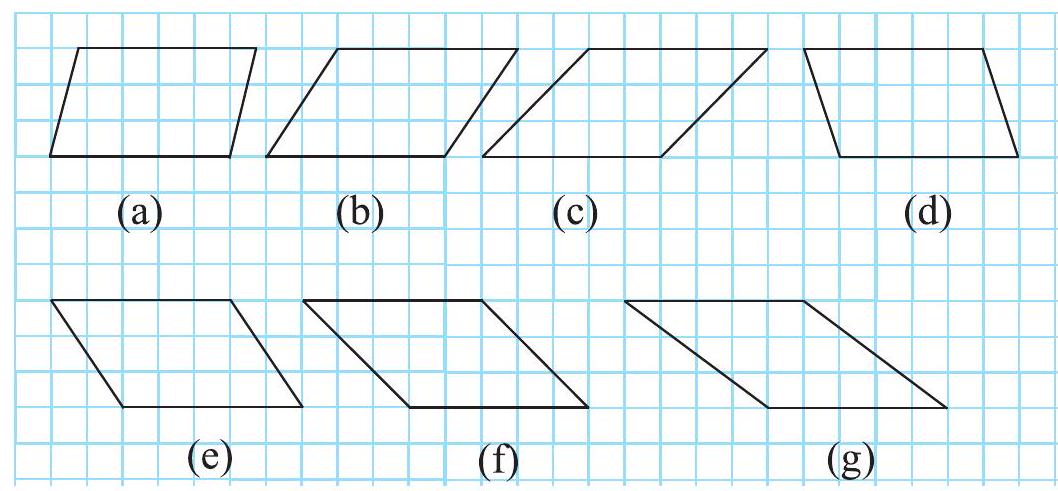
आकृति 9.3
आकृतियों द्वारा घेरे गए वर्गों की संख्या को गिन कर, समांतर चतुर्भुजों का क्षेत्रफल ज्ञात कीजिए और भुजाओं को माप कर परिमाप भी ज्ञात कीजिए।
निम्न तालिका को पूरा कीजिए :
| समांतर चतुर्भुज | आधार | ऊँचाई | क्षेत्रफल | परिमाप |
|---|---|---|---|---|
| (a) | 5 इकाई | 3 इकाई | 15 वर्ग इकाई | |
| (b) | ||||
| (c) | ||||
| (d) | ||||
| (e) | ||||
| (f) | ||||
| (g) |
आप दखेंगे कि इन सभी समांतर चतुर्भुजों का क्षेत्रफल तो समान है परंतु परिमाप अलग-अलग हैं। अब, निम्न
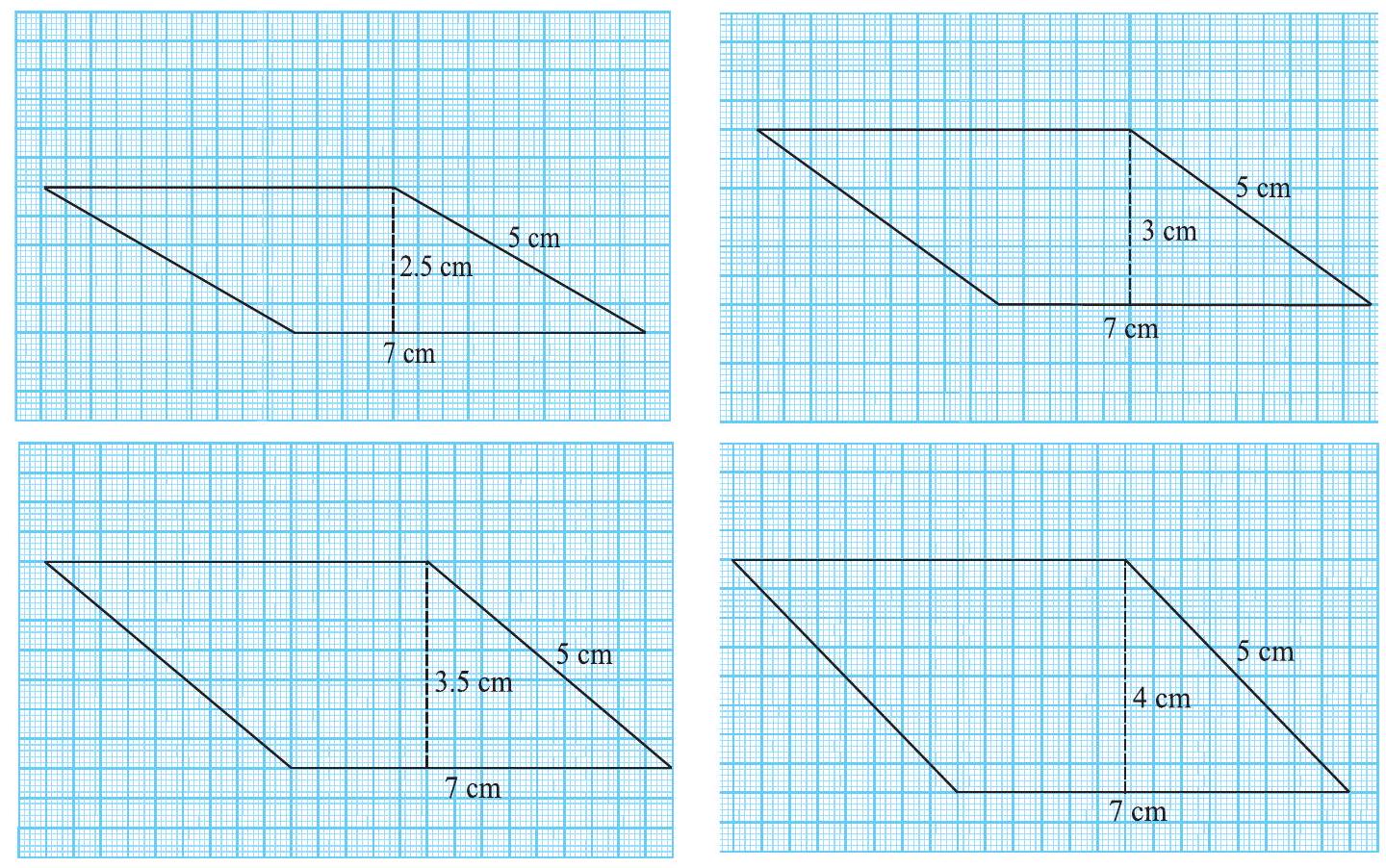
आकृति 9.4
प्रत्येक समांतर चतुर्भुज का परिमाप तथा क्षेत्रफल ज्ञात कीजिए। अपने परिणाम का विश्लेषण कीजिए।
आप देखेंगे कि इन समांतर चतुर्भुजों का क्षेत्रफल अलग-अलग हैं लेकिन परिमाप समान हैं।
समांतर चतुर्भुज का क्षेत्रफल ज्ञात करने के लिए आपको समांतर चतुर्भुज का आधार तथा संगत ऊँचाई को ज्ञात करने की आवश्यकता है।
इन्हें कीजिए
निम्न समांतर चतुर्भुजों के क्षेत्रफल ज्ञात कीजिए

(iii) समांतर चतुर्भुज

9.2 एक त्रिभुज का क्षेत्रफल
एक माली पूरे तिकोने पार्क पर घास लगाने का व्यय जानना चाहता है। इस स्थिति में हमें त्रिभुजाकार क्षेत्र का क्षेत्रफल ज्ञात करने की आवश्यकता है। आइए एक त्रिभुज के क्षेत्रफल को प्राप्त करने की विधि ज्ञात करें। कागज़ के एक टुकड़े पर एक विषमबाहु त्रिभुज बनाइए। इस त्रिभुज को काट लीजिए।

इस त्रिभुज को दूसरे कागज़ के टुकड़े पर रखिए और समान माप का एक ओर त्रिभुज काटिए।
इस प्रकार अब आपके पास समान माप के दो विषमबाहु त्रिभुज हैं। क्या दोनों त्रिभुज सर्वांगसम हैं?
एक त्रिभुज को दूसरे पर रखिए जिससे वे एक-दूसरे को पूर्ण रूप से ढक लें। आप दोनों में से एक त्रिभुज को घुमा भी सकते हैं।
अब दोनों त्रिभुजों को इस प्रकार आपस में रखिए जिससे उनकी संगत भुजाओं का एक युग्म आपस में मिल जाएँ (जैसा आकृति 9.5 में दिखाया गया है)।
क्या इस प्रकार से बनी आकृति एक समांतर चतुर्भुज है?
प्रत्येक त्रिभुज के क्षेत्रफल की तुलना समांतर चतुर्भुज के क्षेत्रफल से कीजिए।
त्रिभुजों के आधार तथा ऊँचाई की तुलना समांतर चतुर्भुज के आधार तथा ऊँचाई से कीजिए।
आप देखेंगे कि दोनों त्रिभुजों के क्षेत्रफलों का योगफल समांतर चतुर्भुज के क्षेत्रफल के बराबर है। त्रिभुज का आधार और ऊँचाई क्रमशः समांतर चतुर्भुज के आधार और ऊँचाई के बराबर है।
प्रत्येक त्रिभुज का क्षेत्रफल
इन्हें कीजिए
1. ऊपर दिए गए क्रियाकलापों को अलग-अलग प्रकार के त्रिभुज लेकर कीजिए।
2. अलग-अलग प्रकार के समांतर चतुर्भुज लीजिए। प्रत्येक समांतर चतुर्भुज को दो त्रिभुजों में एक विकर्ण के अनुदिश काटिए। क्या ये त्रिभुज सर्वांगसम हैं।
आकृति (9.6) में सभी त्रिभुज, आधार
आधार
क्या हम कह सकते हैं कि सभी त्रिभुजों का क्षेत्रफल बराबर है? हाँ। क्या त्रिभुज सर्वांगसम हैं? नहीं।
हम निष्कर्ष निकालते हैं कि सभी सर्वांगसम त्रिभुजों का क्षेत्रफल बराबर होता है लेकिन यह आवश्यक नहीं है कि वे त्रिभुज जिनका क्षेत्रफल बराबर होता है वे सर्वांगसम हैं।
आधार
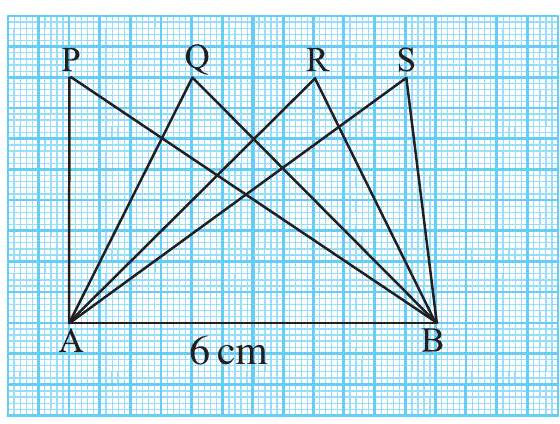
आकृति 9.6
इसकी ऊँचाई

आकृति 9.7
उदाहरण 1 एक समांतर चतुर्भुज की एक भुजा और संगत ऊँचाई क्रमशः
हल
आधार की लंबाई दी गई है

आकृति 9.8
उदाहरण 2 यदि एक समांतर चतुर्भुज (आकृति 9.9) का क्षेत्रफल
हल समांतर चतुर्भुज का क्षेत्रफल
इसलिए,
या
या
इस प्रकार, समांतर चतुर्भुज की ऊँचाई
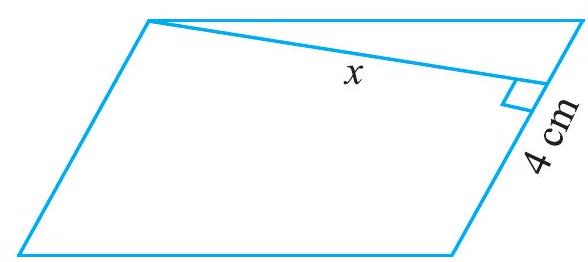
आकृति 9.9
उदाहरण 3 समांतर चतुर्भुज
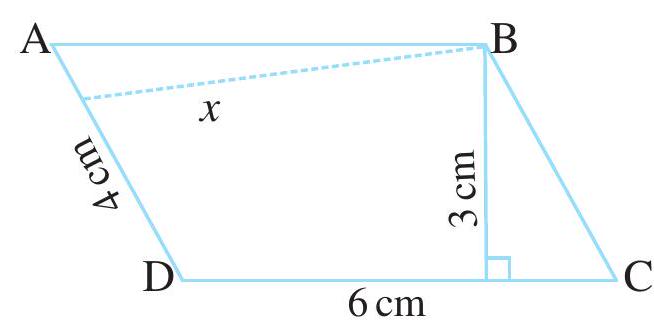
आकृति 9.10
(i) समांतर चतुर्भुज का क्षेत्रफल
(ii) आधार
हल
(i) समांतर चतुर्भुज का क्षेत्रफल
(ii) आधार
ऊँचाई
क्षेत्रफल
समांतर चतुर्भुज का क्षेत्रफल
इसलिए,
इस प्रकार, आधार
उदाहरण 4 निम्न त्रिभुजों का क्षेत्रफल ज्ञात कीजिए (आकृति 9.11) :

आकृति 9.11
हल
(i) त्रिभुज का क्षेत्रफल
(ii) त्रिभुज का क्षेत्रफल
उदाहरण 5
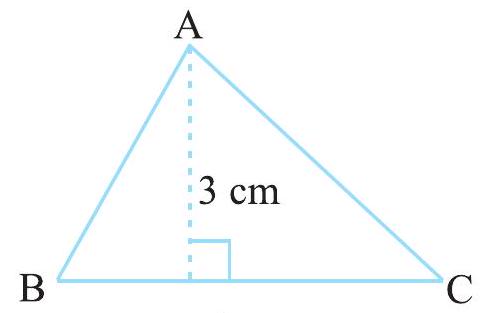
आकृति 9.12
हल
या
इसलिए
उदाहरण 6
और
(i)
(ii)
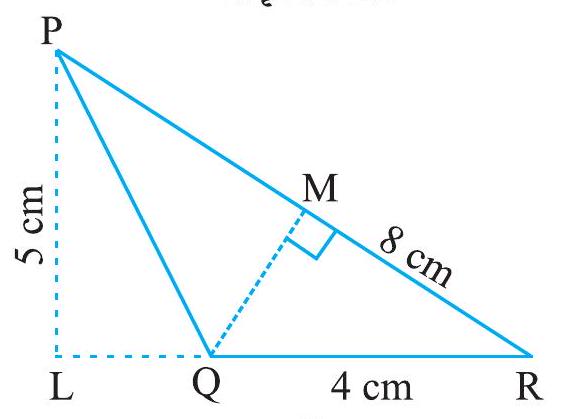
आकृति 9.13
हल (i)
(ii)
त्रिभुज का क्षेत्रफल
प्रश्नावली 9.1
1. निम्न में प्रत्येक समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए :

2. निम्न में प्रत्येक त्रिभुज का क्षेत्रफल ज्ञात कीजिए :

3. रिक्त स्थान का मान ज्ञात कीजिए :
| क्र.सं. | आधार | ऊँचाई | समांतर चतुर्भुज का क्षेत्रफल |
|---|---|---|---|
| a. | |||
| b. | |||
| c. | |||
| d. |
4. रिक्त स्थानों का मान ज्ञात कीजिए :
| आधार | ऊँचाई | त्रिभुज का क्षेत्रफल |
|---|---|---|
| ________ | ||
| ________ | ||
| ________ |
5.
(a) समांतर चतुर्भुज
(b)
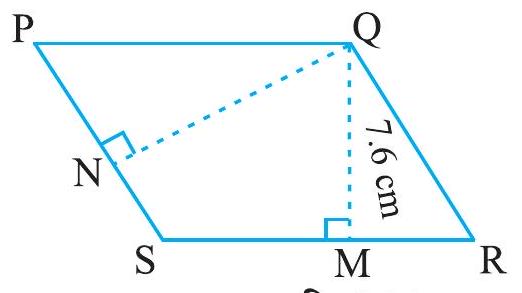
आकृति 9.14
6.
7. त्रिभुज

आकृति 9.16
8.
आकृति 9.17
9.3 वृत्त
एक दौड़ पथ अपने दोनों किनारों पर अर्धवृत्ताकार है (आकृति 9.18)।
क्या आप एक धावक द्वारा तय की गई दूरी ज्ञात कर सकते हैं यदि वह इस दौड़ पथ के दो पूरे चक्कर लगाता है? जब आकार वृत्ताकार हो तो हमें उसके चारों ओर की दूरी प्राप्त करने की एक विधि ज्ञात करने की आवश्यकता होती है।
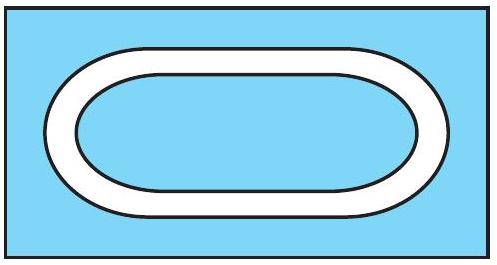
आकृति 9.18
9.3.1 वृत्त की परिधि
तान्या गत्ते के घुमावदार आकार के अलग-अलग कार्ड काटती है। वह इन कार्डों को सजाने के लिए इनके चारों ओर किनारी लगाना चाहती है। प्रत्येक के लिए उसे कितनी लंबी किनारी की आवश्यकता होगी (आकृति 9.19)?

आकृति 9.19
आप एक पैमाने (रूलर) की सहायता से वक्र (curve) को नहीं माप सकते क्योंकि ये आकृतियाँ सीधी नहीं हैं। आप क्या करेंगे?
आकृति 9. 19(a) में दिए गए आकार की आवश्यक किनारी की लंबाई ज्ञात करने के लिए आपको एक तरीका बताया जा रहा है। कार्ड के किनारे पर एक बिंदु अंकित कीजिए और इसे एक टेबल पर रखिए। बिंदु की स्थिति को टेबल पर भी अंकित कीजिए (आकृति 9.20)।
आकृति 9.20
अब वृत्ताकार कार्ड को एक सरल रेखा की दिशा में टेबल पर तब तक घुमाइए जब तक अंकित बिंदु टेबल को दुबारा स्पर्श न कर जाए। इस दूरी को रेखा के अनुदिश में मापिए। यह आवश्यक किनारी की लंबाई है। यह कार्ड के अंकित किए गए बिंदु से कार्ड के किनारे-किनारे वापस उसी बिंदु तक की दूरी है।

आकृति 9.21
आप एक धागे को वृत्ताकार वस्तु के चारों ओर किनारे-किनारे रख कर भी दूरी ज्ञात कर सकते हैं।
एक वृत्ताकार क्षेत्र के चारों ओर की दूरी इसकी परिधि कहलाती है।
इन्हें कीजिए
एक बोतल का ढक्कन, एक चूड़ी या कोई अन्य वृत्ताकार वस्तु लीजिए और इसकी परिधि ज्ञात कीजिए।
अब, क्या आप इस विधि से एक धावक द्वारा एक पथ पर तय की गई दूरी ज्ञात कर सकते है? अभी भी, पथ के चारों ओर की दूरी ज्ञात करना या अन्य किसी वृत्ताकार वस्तु को धागे से मापना बहुत ही मुश्किल होगा। तथापि यह माप सही नहीं होगी।
अतः इसके लिए हमें एक सूत्र की आवश्यकता है जैसाकि तल की आकृति या आकारों के लिए हम प्रयोग करते हैं।
आइए हम देखें क्या वृत्तों के व्यास और परिधि के बीच में कोई संबंध है।
निम्न तालिका पर विचार कीजिए। अलग-अलग त्रिज्याओं के 6 वृत्त खींचिए और धागे की सहायता से उनकी परिधि ज्ञात कीजिए। परिधि और व्यास के अनुपात को भी ज्ञात कीजिए:
| वृत्त | त्रिज्या | व्यास | परिधि | परिधि और व्यास का अनुपात |
|---|---|---|---|---|
| 1. | ||||
| 2. | ||||
| 3. | ||||
| 4. | ||||
| 5. | ||||
| 6. |
ऊपर दी गई तालिका से आप क्या निष्कर्ष निकालते हैं? क्या यह अनुपात लगभग समान है? हाँ। क्या आप कह सकते हैं कि एक वृत्त की परिधि हमेशा इसके व्यास की तीन गुणा है? हाँ।
यह अनुपात स्थिर है और इसे ’
अतः हम कह सकते हैं
हम जानते हैं कि एक वृत्त का व्यास
अत:
या
इन्हें कीजिए
आकृति 9.22 में
(a) किस वर्ग का परिमाप अधिक है ?
(b) कौन-सा अधिक है, छोटे वर्ग का परिमाप या वृत्त की परिधि?
आकृति 9.22
प्रयास कीजिए
एक चौथाई प्लेट तथा एक अर्ध प्लेट लीजिए। प्रत्येक को टेबल की ऊपरी सतह पर एक बार घुमाइए। कौन-सी प्लेट एक पूरे चक्कर में अधिक दूरी तय करती है? कौन-सी प्लेट कम चक्कर में टेबल की ऊपरी सतह की लंबाई को पूरा करेगी?

उदाहरण 7
हल वृत्त का व्यास
अतः,
उदाहरण 8 एक वृत्ताकार तश्तरी (disc) की परिधि ज्ञात कीजिए जिसकी त्रिज्या
हल वृत्ताकार तश्तरी (disc) की त्रिज्या
अतः, वृत्ताकार तश्तरी की परिधि
उदाहरण 9 एक वृत्ताकार पाइप की त्रिज्या
हल
आवश्यक टेप की लंबाई, पाइप की परिधि के बराबर है।
इसलिए, पाइप के चारों ओर एक बार टेप लपेटने की आवश्यक लंबाई
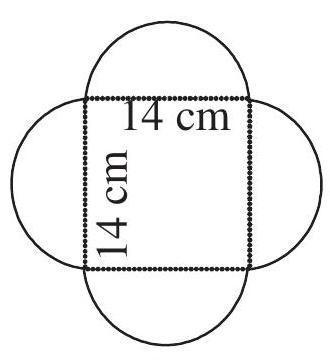
उदाहरण 10 दी गई आकृति का परिमाप ज्ञात कीजिए (आकृति 9.23)।
आकृति 9.23
हल इस आकृति में हमें वर्ग के प्रत्येक ओर स्थित अर्धवृत्त की परिधि को ज्ञात करने की आवश्यकता है। क्या आपको वर्ग के परिमाप को भी ज्ञात करने की आवश्यकता है? नहीं। इस आकृति की बाह्य परिसीमा अर्धवृत्तों से मिलकर बनी है।
प्रत्येक अर्धवृत्त का व्यास
हम जानते हैं कि, वृत्त की परिधि
प्रत्येक अर्धवृत्त की परिधि
उदाहरण 11 सुधांशु
(प्रयोग करें
हल अर्धवृत्ताकार तश्तरी (disc) के परिमाप को ज्ञात करने के लिए, (आकृति 9.24), हमें ज्ञात करने की आवश्यकता है:
(i) अर्धवृत्ताकार आकार की परिधि
(ii) व्यास
आकृति 9.24
दी गई त्रिज्या
हम जानते हैं कि वृत्त की परिधि
इसलिए, वृत्त का व्यास
अतः प्रत्येक अर्धवृत्ताकार तश्तरी (disc) का परिमाप
9.3.2 वृत्त का क्षेत्रफल
निम्न पर विचार कीजिए :
-
एक किसान खेत के केंद्र पर
-
10 रु प्रति
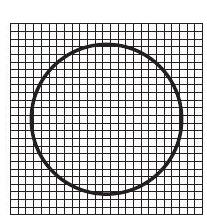
क्या आप बता सकते हैं कि इन स्थितियों में हमें क्या ज्ञात करने की आवश्यकता है, क्षेत्रफल या परिमाप? ऐसी स्थितियों में हमें वृत्ताकार क्षेत्र का क्षेत्रफल ज्ञात करने की आवश्यकता होती है। आइए ग्राफ़ पेपर की सहायता से हम एक वृत्त का क्षेत्रफल ज्ञात करते हैं।
आकृति 9.25
क्योंकि किनारे सीधे नहीं हैं, हमें, इस विधि से, वृत्त के क्षेत्रफल का एक कच्चा (rough) अनुमान ही प्राप्त होता है। एक और विधि से वृत्त का क्षेत्रफल ज्ञात करते हैं।
एक वृत्त बनाइए और उसके अर्धभाग को छायांकित कीजिए [आकृति 9.26(i)] अब वृत्त को आठ भागों में मोड़िए और उन्हें मुड़ी हुई तहों के अनुदिश में काटिए (आकृति 9.26(ii))।

आकृति 9.26
अलग-अलग टुकड़ों को, जैसा आकृति 9.27 में दिखाया गया है, व्यवस्थित कीजिए, जो एक स्थूल रूप से (roughly) समांतर चतुर्भुज को दर्शाता है।
आकृति 9.27
जितने अधिक त्रिज्याखंड होंगे, उतना ही सही समांतर चतुर्भुज हमें प्राप्त होता है।
जैसा ऊपर किया गया है यदि हम वृत्त को 64 त्रिज्याखंडों में विभाजित करें और उन्हें व्यवस्थित करें, तो हमें लगभग एक आयत प्राप्त होता है (आकृति 9.28)।

आकृति 9.28
इस आयत की चौड़ाई क्या है? इस आयत की चौड़ाई वृत्त की त्रिज्या ही है अर्थात् ’
जैसाकि पूरे वृत्त को 64 त्रिज्याखंडों में विभाजित किया गया तथा प्रत्येक ओर 32 त्रिज्यखंड हैं। आयत की लंबाई 32 त्रिज्यखंडों की लंबाइयों के बराबर है जो वृत्त की परिधि की आधी है (आकृति 9.28)।
इनें कीजिए
ग्राफ़ पेपर पर अलग-अलग त्रिज्याओं के वृत्तों को बनाइए। वर्गों की संख्या को गिनकर क्षेत्रफल ज्ञात कीजिए। सूत्र का प्रयोग करके भी क्षेत्रफल ज्ञात कीजिए। दोनों उत्तरों की तुलना कीजिए।
वृत्त का क्षेत्रफल
अतः, वृत्त का क्षेत्रफल
उदाहरण 12
हल त्रिज्या
वृत्त का क्षेत्रफल
उदाहरण 13 एक वृत्ताकार बगीचे का व्यास
हल व्यास,
वृत्त का क्षेत्रफल
उदाहरण 14 संलग्न आकृति दो वृत्तों को दर्शाती है जिनका केंद्र समान है। बड़े वृत्त की त्रिज्या
ज्ञात कीजिए
(a) बड़े वृत्त का क्षेत्रफल
(b) छोटे वृत्त का क्षेत्रफल
(c) दोनों वृत्तों के बीच छायांकित भाग का क्षेत्रफल
हल
(a) बड़े वृत्त की त्रिज्या
अतः, बड़े वृत्त का क्षेत्रफल
(b) छोटे वृत्त की त्रिज्या
छोटे वृत्त का क्षेत्रफल
(c) छायांकित भाग का क्षेत्रफल

प्रश्नावली 9.2
1. निम्न त्रिज्याओं वाले वृत्तों की परिधि ज्ञात कीजिए (
(a)
(b)
(c)
2. निम्न वृत्तों का क्षेत्रफल ज्ञात कीजिए। दिया गया है :
(a) त्रिज्या
(b) व्यास
(c) त्रिज्या
3. यदि एक वृत्ताकार शीट की परिधि
4.
5.
6. साइमा
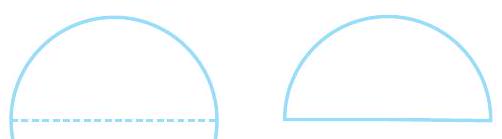
7. दी गई आकृति, व्यास के साथ एक अर्धवृत्त है। उसका परिमाप ज्ञात कीजिए।
8. 15 रु प्रति वर्ग मीटर की दर से,
9. शाझली
कौन-सी आकृति अधिक क्षेत्रफल घेरती है वृत्त या वर्ग ? (
10.
(

11.
12. एक वृत्त की परिधि

13. एक वृत्ताकार फूलों की क्यारी के चारों ओर

14. एक वृत्ताकार फूलों के बगीचे का क्षेत्रफल

15. आकृति में, अंतः और बाह्य वृत्तों की परिधि ज्ञात कीजिए। (
16.
17. एक वृत्ताकार घड़ी की मिनट की सुई की लंबाई
हमने क्या चर्चा की?
1. एक समांतर चतुर्भुज का क्षेत्रफल
2. एक त्रिभुज का क्षेत्रफल
3. एक वृत्ताकार क्षेत्र के चारों ओर की दूरी इसकी परिधि कहलाती है। एक वृत्त की परिधि