8.1 भूमिका

आपने संख्याओं का अध्ययन अपने परिवेश की वस्तुओं के गिनने से प्रारंभ किया। इस कार्य में प्रयोग की गई संख्याओं को गणन संख्याएँ (counting numbers) या प्राकृत संख्याएँ (natural numbers) कहा गया था। ये हैं 1, 2,3, 4, …। प्राकृत संख्याओं में 0 को सम्मिलित करने पर हमें पूर्ण संख्याएँ (whole numbers), अर्थात् $0,1,2,3,\dots$ प्राप्त हुई। इसके बाद, पूर्णांक (integers) प्राप्त करने के लिए, पूर्ण संख्याओं में प्राकृत संख्याओं के ॠणात्मकों (negatives) को सम्मिलित किया गया। … -3, $-2,-1,0,1,2,3\dots$ पूर्णांक हैं। इस प्रकार, हमने संख्या पद्धति (number system) को प्राकृत संख्याओं से पूर्ण संख्याओं तक और पूर्ण संख्याओं से पूर्णांकों तक विस्तृत किया।

आपका भिन्नों (fractions) से भी परिचय कराया गया था। ये $\frac{\text{ अंश }}{\text{ हर }}\left(\frac{\text{ numerator }}{\text{ denominator }}\right)$, के प्रकार की संख्याएँ होती हैं, जहाँ अंश या तो $0$ या एक धनात्मक पूर्णांक होता है तथा हर, एक धनात्मक पूर्णांक होता है। आपने दो भिन्नों की तुलना की, उनके समतुल्य (equivalent) रूप (भिन्नें) ज्ञात किए तथा उन पर सभी चारों आधारभूत संक्रियाओं योग, व्यवकलन (घटाना), गुणन और विभाजन का अध्ययन किया।

इस अध्याय में, हम संख्या पद्धति का और आगे विस्तार करेंगे। हम परिमेय संख्याओं (rational numbers) की अवधारणा का परिचय देकर उन पर योग, व्यवकलन, गुणन और विभाजन (भाग) की संक्रियाएँ करना सीखेंगे।

8.2 परिमेय संख्याओं की आवश्यकता

पहले हम देख चुके हैं कि किस प्रकार संख्याओं से संबद्ध विपरीत (opposite) स्थितियों को व्यक्त करने के लिए पूर्णांकों का प्रयोग किया जा सकता है। उदाहरणार्थ, यदि एक स्थान के दाईं ओर $3\mathrm{km}$ दूरी को 3 से व्यक्त किया जाए, तो उसी स्थान से बाईं ओर की $5\mathrm{km}$ दूरी को $-5$ से व्यक्त किया जा सकता है। यदि $150$ रु के लाभ को $150$ से व्यक्त किया जाए, तो $100$ रु की हानि को $-100$ से व्यक्त किया जा सकता है।

इसी प्रकार की अनेक स्थितियाँ होती हैं, जिनमें भिन्नात्मक संख्याएँ (भिन्न) संबद्ध होती हैं।

हम समुद्र तल से ऊपर $750\mathrm{m}$ की ऊँचाई को $\frac{3}{4}\mathrm{km}$ से व्यक्त कर सकते हैं। क्या हम समुद्र तल से नीचे $750\mathrm{m}$ की गहराई को $\mathrm{km}$ में व्यक्त कर सकते हैं?

क्या हम समुद्र तल से नीचे $\frac{3}{4}\mathrm{km}$ की गहराई को $\frac{-3}{4}$ से व्यक्त कर सकते हैं? हम देख सकते हैं कि $\frac{-3}{4}$ न तो एक पूर्णांक है और न ही एक भिन्न। ऐसी संख्याओं को सम्मिलित करने के लिए, हमें संख्या पद्धति को विस्तृत करने की आवश्यकता है।

8.3 परिमेय संख्याएँ क्या हैं ?

शब्द ‘परिमेय’ (rational) की उत्पत्ति, पद ‘अनुपात’ (ratio) से हुई है। आप जानते हैं कि अनुपात $3:2$ को $\frac{3}{2}$ भी लिखा जा सकता है। यहाँ 3 और 2 प्राकृत संख्याएँ हैं।

इसी प्रकार, दो पूर्णांकों $p$ और $q(q\ne 0)$ के अनुपात $p:q$ को $\frac{p}{q}$ लिखा जा सकता है। यही वह रूप है जिसमें परिमेय संख्याएँ व्यक्त की जाती हैं।

एक परिमेय संख्या को ऐसी संख्या के रूप में परिभाषित किया जाता है, जिसे $\frac{p}{q}$, के रूप में व्यक्त किया जा सके, जहाँ $p$ और $q$ पूर्णांक हैं तथा $q\ne 0$ है।

इस प्रकार, $\frac{4}{5}$ एक परिमेय संख्या है। यहाँ $p=4$ है और $q=5$ है।

क्या $\frac{-3}{4}$ भी एक परिमेय संख्या है? हाँ, क्योंकि $p=-3$ और $q=4$ पूर्णांक हैं।

$\bullet$ आपने $\frac{3}{8},\frac{4}{8},1\frac{2}{3}$, इत्यादि जैसी अनेक भिन्न देखी हैं। सभी भिन्न परिमेय संख्याएँ होती हैं। क्या आप इसका कारण बता सकते हैं? दशमलव संख्याओं $0.5,2.3,0.333$ इत्यादि के बारे में क्या कहा जा सकता है? इस प्रकार की प्रत्येक संख्या को एक सामान्य भिन्न के रूप में लिखा जा सकता है और इसीलिए ये परिमेय संख्याएँ हैं। उदाहरणार्थ, $0.5=\frac{5}{10},2.3=\frac{23}{10}$, $0.333=\frac{333}{1000}$ इत्यादि।

प्रयास कीजिए

1. क्या संख्या $\frac{2}{-3}$ परिमेय संख्या है? इसके बारे में सोचिए।

2. दस परिमेय संख्याओं की एक सूची बनाइए।

अंश और हर

$\frac{p}{q}$ में, पूर्णांक $p$ अंश है तथा पूर्णांक $q(\ne 0)$ हर है।

इस प्रकार, $\frac{-3}{7}$ में, -3 अंश है और 7 हर है।

ऐसी पाँच परिमेय संख्याएँ लिखिए, जिनमें से प्रत्येक का

(a) अंश एक ॠणात्मक पूर्णांक हो और हर एक धनात्मक पूर्णांक हो।

(b) अंश एक धनात्मक पूर्णांक हो और हर एक ॠणात्मक पूर्णांक हो।

(c) अंश और हर दोनों ॠणात्मक पूर्णांक हों।

(d) अंश और हर दोनों धनात्मक पूर्णांक हों।

$\bullet$ क्या पूर्णांक भी परिमेय संख्याएँ हैं?

किसी भी पूर्णांक को एक परिमेय संख्या माना जा सकता है। उदाहरणार्थ, पूर्णांक -5 एक परिमेय संख्या है, क्योंकि आप इसे $\frac{-5}{1}$ के रूप में लिख सकते हैं। पूर्णांक $0$ को भी $0=\frac{0}{2}$ या $\frac{0}{7}$ इत्यादि के रूप में लिखा जा सकता है। अतः यह भी एक परिमेय संख्या है।

इस प्रकार, परिमेय संख्याओं में पूर्णांक और भिन्न सम्मिलित होते हैं।

समतुल्य परिमेय संख्याएँ

एक परिमेय संख्या को अलग-अलग अंशों और हरों का प्रयोग करते हुए लिखा जा सकता है।

उदाहरणार्थ, परिमेय संख्या $\frac{-2}{3}$ पर विचार कीजिए।

$\frac{-2}{3}=\frac{-2\times 2}{3\times 2}=\frac{-4}{6}\text{ । हम देखते हैं कि }\frac{-2}{3}\text{ वही है जो }\frac{-4}{6}\text{ है। }$

साथ ही, $\frac{-2}{3}=\frac{(-2)\times (-5)}{3\times (-5)}=\frac{10}{-15}$ है। अतः, $\frac{-2}{3}$ वही है जो $\frac{10}{-15}$ है।

इस प्रकार, $\frac{-2}{3}=\frac{10}{-15}=\frac{10}{-15}$ है। ऐसी परिमेय संख्याएँ जो परस्पर बराबर हों एक दूसरे के समतुल्य (equivalent) या तुल्य कही जाती हैं।

$\text{ पुन:, }\frac{10}{-15}=\frac{-10}{15}(\text{ कैसे?) }$

प्रयास कीजिए

रिक्त स्थानों को भरिए :

(i) $\frac{5}{4}=\frac{◻}{16}=\frac{25}{◻}=\frac{-15}{◻}$

(ii) $\frac{-3}{7}=\frac{◻}{14}=\frac{9}{◻}=\frac{-6}{◻}$

एक परिमेय संख्या के अंश और हर को एक ही शून्येतर (non-zero) पूर्णांक से गुणा करने पर, हमें दी हुई परिमेय संख्या के समतुल्य (या तुल्य) एक अन्य परिमेय संख्या प्राप्त होती है। यह ठीक समतुल्य भिन्न प्राप्त करने जैसा ही है।

गुणा की तरह, एक ही शून्येतर पूर्णांक से अंश और हर को भाग देने पर भी समतुल्य परिमेय संख्याएँ प्राप्त होती हैं। उदाहरणार्थ,

$\frac{10}{-15}=\frac{10÷(-5)}{-15÷(-5)}=\frac{-2}{3},\frac{-12}{24}=\frac{-12÷12}{24÷12}=\frac{-1}{2}$

$\frac{-2}{3}\text{ को }-\frac{2}{3},\frac{-10}{15}\text{ को }-\frac{10}{15}\text{ इत्यादि, लिखते हैं। }$

8.4 धनात्मक और ॠणात्मक परिमेय संख्याएँ

परिमेय संख्या $\frac{2}{3}$ पर विचार कीजिए। इस संख्या के अंश और हर दोनों ही धनात्मक पूर्णांक हैं। ऐसी परिमेय संख्या को एक धनात्मक परिमेय संख्या कहते हैं। अतः, $\frac{3}{8},\frac{5}{7},\frac{2}{9}$ इत्यादि धनात्मक परिमेय संख्याएँ हैं।

$\frac{-3}{5}$ का अंश एक ॠणात्मक पूर्णांक है, जबकि इसका हर एक धनात्मक पूर्णांक है। ऐसी परिमेय संख्या को ॠणात्मक परिमेय संख्या कहते हैं। अत: $\frac{-5}{7},\frac{-3}{8},\frac{-9}{5}$ इत्यादि ॠणात्मक परिमेय संख्याएँ हैं।

प्रयास कीजिए

1. क्या 5 एक धनात्मक परिमेय संख्या है?

2. पाँच और धनात्मक परिमेय संख्याएँ लिखिए।

प्रयास कीजिए

1. क्या -8 एक ॠणात्मक परिमेय संख्या है।

2. पाँच और ॠणात्मक परिमेय संख्याएँ लिखिए। परिमेय संख्याएँ हैं।

$\bullet$ क्या $\frac{8}{-3}$ एक ॠणात्मक संख्या है? हम जानते हैं कि $\frac{8}{-3}=\frac{8\times (-1)}{-3\times (-1)}=\frac{-8}{3}$ है, तथा $\frac{-8}{3}$ एक ॠणात्मक परिमेय संख्या है। अतः, $\frac{8}{-3}$ एक ॠणात्मक परिमेय संख्या है।

इसी प्रकार, $\frac{5}{-7},\frac{6}{-5},\frac{2}{-9}$ इत्यादि सभी ॠणात्मक परिमेय संख्याएँ हैं। ध्यान दीजिए कि इनके अंश धनात्मक हैं तथा हर ॠणात्मक हैं।

$\bullet$ संख्या 0 न तो एक धनात्मक परिमेय संख्या है और न ही एक ॠणात्मक परिमेय संख्या।

$\bullet$ $\frac{-3}{-5}$ के बारे में क्या कहा जा सकता है?

आप देखेंगे कि $\frac{-3}{-5}=\frac{-3\times (-1)}{-5\times (-1)}=\frac{3}{5}$ है। अतः $\frac{-3}{-5}$ एक धनात्मक परिमेय संख्या है। इस प्रकार, $\frac{-2}{-5},\frac{-5}{-3}$, इत्यादि धनात्मक परिमेय संख्याएँ हैं।

प्रयास कीजिए

निम्नलिखित में से कौन-सी संख्याएँ ॠणात्मक परिमेय संख्याएँ हैं?

(i) $\frac{-2}{3}$

(ii) $\frac{5}{7}$

(iii) $\frac{3}{-5}$

(iv) $0$

(v) $\frac{6}{11}$

(vi) $\frac{-2}{-9}$

8.5 एक संख्या रेखा पर परिमेय संख्याएँ

आप यह जानते हैं कि एक संख्या रेखा पर पूर्णांकों को किस प्रकार निरूपित किया जाता है। आइए ऐसी ही एक संख्या रेखा खींचें।

$0$ के दाईं ओर के बिंदुओं को + चिह्न से व्यक्त करते हैं और ये धनात्मक पूर्णांक दर्शाते हैं। $0$ से बाईं ओर के बिंदुओं को - चिह्न से व्यक्त करते हैं और ये ॠणात्मक पूर्णांक दर्शाते हैं। संख्या रेखा पर भिन्नों के निरूपण से भी आप परिचित हैं।

आइए अब देखें कि परिमेय संख्याएँ संख्या रेखा पर किस प्रकार निरूपित की जा सकती हैं?

आइए संख्या रेखा पर संख्या $-\frac{1}{2}$ को निरूपित करें।

जैसा कि धनात्मक पूर्णांकों की स्थिति में किया गया था, धनात्मक परिमेय संख्याओं को $0$ के दाईं ओर अंकित किया जाएगा तथा ॠणात्मक परिमेय संख्याओं को $0$ के बाईं ओर अंकित किया जाएगा।

$0$ के किस ओर आप $-\frac{1}{2}$ को अंकित करेंगे? ॠणात्मक परिमेय संख्या होने के कारण इसे $0$ के बाईं ओर अंकित किया जाएगा।

आप जानते हैं कि संख्या रेखा पर पूर्णांकों को अंकित करते समय, उत्तरोत्तर पूर्णांकों को समान अंतरालों पर अंकित किया जाता है। साथ ही, संख्याओं $1$ और $-1$ का युग्म संख्या $0$ से समदूरस्थ हैं। इसी प्रकार, $2$ और $-2$ तथा $3$ और $-3$ भी समदूरस्थ हैं।

इसी प्रकार, परिमेय संख्याएँ $\frac{1}{2}$ और $-\frac{1}{2}$ भी $0$ से समदूरस्थ होंगी। हम जानते हैं कि परिमेय संख्या $\frac{1}{2}$ को किस प्रकार संख्या रेखा पर अंकित किया जाता है। यह उस बिंदु पर अंकित किया

जाता है, जो $0$ और $1$ से बराबर दूरी (ठीक बीच में) पर है। अर्थात् $0$ और $1$ की आधी दूरी पर है। इसलिए, $-\frac{1}{2}$ को $0$ और $-1$ की आधी दूरी पर अंकित किया जाएगा।

हम जानते हैं कि $\frac{3}{2}$ को संख्या रेखा पर किस प्रकार अंकित किया जाता है। इसे $0$ के दाईं ओर $1$ और $2$ के बीच में आधी दूरी पर अंकित किया जाता है। आइए अब संख्या रेखा पर $\frac{-3}{2}$ को अंकित करें। यह $0$ के बाईं ओर उतनी ही दूरी पर अंकित होगा जितनी दूरी $0$ और $\frac{3}{2}$ के बीच है।

घटते हुए क्रम में $\frac{-1}{2},\frac{-2}{2}(=-1),\frac{-3}{2},\frac{-4}{2}(=-2)$, इत्यादि प्राप्त हैं। इससे यह प्रदर्शित होता है कि $\frac{-3}{2}$ संख्याओं -1 और -2 के बीच में आधी दूरी पर स्थित (या अंकित) होगा।

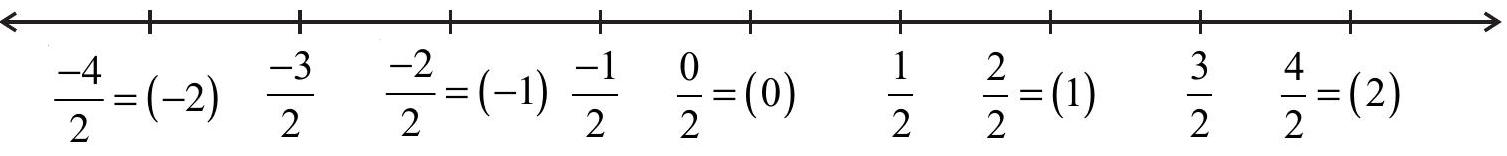
इसी प्रकार, $\frac{-5}{2}$ और $\frac{-7}{2}$ को संख्या रेखा पर अंकित कीजिए।

इसी प्रकार, $-\frac{1}{3}$ संख्या रेखा पर 0 के बाईं ओर शून्य से उतनी ही दूरी पर होगी जितनी कि $\frac{1}{3}$ शून्य से दाईं ओर है।

अतः जैसा कि ऊपर किया गया है, $-\frac{1}{3}$ को संख्या रेखा पर निरूपित किया जा सकता है। एक बार, हमें $-\frac{1}{3}$ को संख्या रेखा पर निरूपित करना आ जाए तो, हम $-\frac{2}{3},-\frac{4}{3},-\frac{5}{3},\dots$ इत्यादि को संख्या रेखा पर निरूपित कर सकते हैं। विभिन्न हरों वाली अन्य परिमेय संख्याओं को भी इसी प्रकार संख्या रेखा पर निरूपित किया जा सकता है।

8.6 मानक रूप में परिमेय संख्याएँ

निम्नलिखित परिमेय संख्याओं को देखिए :

$\frac{3}{5},\frac{-5}{8},\frac{2}{7},\frac{-7}{11}$

इन सभी परिमेय संख्याओं के हर धनात्मक पूर्णांक हैं तथा अंश और हरों के बीच में केवल $1$ सार्व गुणनखंड (common factor) है। साथ ही, ॠणात्मक चिह्न (-) केवल अंश में ही स्थित है।

ऐसी परिमेय संख्याओं को मानक रूप (standard form) में व्यक्त की गई परिमेय संख्याएँ कहा जाता है।

एक परिमेय संख्या मानक रूप में व्यक्त की हुई कही जाती है, यदि उसका हर धनात्मक पूर्णांक हो तथा उसके अंश और हर में 1 के अतिरिक्त कोई सार्व गुणनखंड न हो।

यदि कोई परिमेय संख्या मानक रूप में नहीं है, तो उसे उसके मानक रूप में व्यक्त किया जा सकता है।

स्मरण कीजिए कि भिन्नों को उनके न्यूनतम रूपों में व्यक्त करने के लिए, हमने उनके अंशों और हरों को एक ही शून्येतर पूर्णांक से भाग दिया था। हम इसी विधि का प्रयोग परिमेय संख्याओं को उनके मानक रूपों में व्यक्त करने में करेंगे।

उदाहरण 1 $\frac{-45}{30}$ को मानक रूप में व्यक्त कीजिए।

हल

$\text{ हमें प्राप्त है : }\frac{-45}{30}=\frac{-45÷3}{30÷3}=\frac{-15}{10}=\frac{-15÷5}{10÷5}=\frac{-3}{2}$

हमें दो बार भाग देना पड़ा। पहली बार 3 से और फिर 5 से। इसे निम्नलिखित प्रकार से भी किया जा सकता था :

$\frac{-45}{30}=\frac{-45÷15}{30÷15}=\frac{-3}{2}$

इस उदाहरण में देखिए कि $15$ , संख्याओं $45$ और $30$ का म.स. है।

इस प्रकार, एक परिमेय संख्या को मानक रूप में व्यक्त करने के लिए, हम उसके अंश और हर को उनके म.स. से, ॠण चिह्न पर बिना कोई ध्यान दिए (यदि कोई हो), भाग देते हैं। (ऋण चिह्न पर ध्यान ना देने का कारण हम अगली कक्षाओं में पढ़ेंगे)

यदि हर में ॠणात्मक चिह्न है, तो ‘-म.स.’ से भाग दीजिए।

उदाहरण 2 मानक रूप में बदलिए :

(i) $\frac{36}{-24}$

(ii) $\frac{-3}{-15}$

हल

(i) $36$ और $24$ का म.स. $12$ है।

अतः, मानक रूप अंश और हर को $-12$ से भाग देने पर प्राप्त होगा।

इस प्रकार, $\frac{36}{-24}=\frac{36÷(-12)}{-24÷(-12)}=\frac{-3}{2}$

(ii) $3$ और $15$ का म.स. $3$ है।

इस प्रकार, $\frac{-3}{-15}=\frac{-3÷(-3)}{-15÷(-3)}=\frac{1}{5}$

प्रयास कीजिए

मानक रूप ज्ञात कीजिए

(i) $\frac{-18}{45}$

(ii) $\frac{-12}{18}$

8.7 परिमेय संख्याओं की तुलना

हम यह जानते हैं कि दो पूर्णांकों या दो भिन्नों की तुलना किस प्रकार की जाती है तथा यह भी कि इनमें कौन बड़ा है और कौन छोटा। आइए अब देखें कि दो परिमेय संख्याओं की तुलना किस प्रकार की जा सकती है।

$\bullet$ $\frac{2}{3}$ और $\frac{5}{7}$ जैसी दो धनात्मक परिमेय संख्याओं की तुलना ठीक उसी प्रकार की जा सकती है, जैसा कि हम भिन्नों की स्थिति के लिए पहले पढ़ चुके हैं।

$\bullet$ मेरी ने दो ॠणात्मक परिमेय संख्याओं $-\frac{1}{2}$ और $-\frac{1}{5}$ की तुलना संख्या रेखा का प्रयोग करते हुए की। उसे ज्ञात था कि दो पूर्णांकों में वह पूर्णांक बड़ा था जो दूसरे पूर्णांक के दाईं ओर स्थित था।

उदाहरणार्थ, संख्या रेखा पर पूर्णांक 5 पूर्णांक 2 के दाईं ओर स्थित है तथा $5>2$ है। संख्या रेखा पर पूर्णांक -2 पूर्णांक -5 के दाईं ओर स्थित है तथा $-2>-5$ है।

उसने इस विधि का प्रयोग परिमेय संख्याओं के लिए भी किया। उसे पता था कि संख्या रेखा पर परिमेय संख्याओं को किस प्रकार अंकित (निरूपित) किया जाता है। उसने $-\frac{1}{2}$ और $-\frac{1}{5}$ को नीचे दर्शाए अनुसार अंकित किया:

क्या उसने दोनों बिंदु सही प्रकार से अंकित किए हैं? उसने कैसे और क्यों $-\frac{1}{2}$ को $-\frac{5}{10}$

तथा $-\frac{1}{5}$ को $-\frac{2}{10}$ में बदला? उसे ज्ञात हुआ कि परिमेय संख्या $-\frac{1}{5}$ परिमेय संख्या

$-\frac{1}{2}$ के दाईं ओर स्थित है। इस प्रकार, $-\frac{1}{5}>-\frac{1}{2}$ है या $-\frac{1}{2}<-\frac{1}{5}$ है।

क्या आप $-\frac{3}{4}$ और $-\frac{2}{3}$ की तथा $-\frac{1}{3}$ और $-\frac{1}{5}$ की तुलना कर सकते हैं? हम भिन्नों के अपने अध्ययन से यह

जानते हैं कि $\frac{1}{5}<\frac{1}{2}$ है। साथ ही, मेरी ने $-\frac{1}{2}$ और $-\frac{1}{5}$ के लिए क्या प्राप्त किया? क्या यह इसका ठीक विपरीत नहीं था।

आप देखते हैं कि $\frac{1}{2}>\frac{1}{5}$ है, परंतु $-\frac{1}{2}<-\frac{1}{5}$ है।

क्या आप $-\frac{3}{4}$ और $-\frac{2}{3}$ तथा $-\frac{1}{2}$ और $-\frac{1}{5}$ के लिए भी इसी प्रकार का परिणाम देखते हैं? मेरी को याद आता है कि उसने पूर्णांकों में पढ़ा था कि $4>3$ है, परंतु $-4<-3$ है; $5>2$ है, परंतु $-5<-2$ इत्यादि।

$\bullet$ ॠणात्मक परिमेय संख्याओं के युग्मों की स्थिति भी ठीक इसी प्रकार है। दो ॠणात्मक परिमेय संख्याओं की तुलना करने के लिए, हम उनकी तुलना उनके चिह्नों को छोड़ते हुए करते हैं और बाद में असमिका (inequality) के चिह्न को उल्टा कर (बदल) देते हैं। उदाहरणार्थ, $-\frac{7}{5}$ और $-\frac{5}{3}$, की तुलना करने के लिए, पहले हम $\frac{7}{5}$ और $\frac{5}{3}$ की तुलना करते हैं। हमें $\frac{7}{5}<\frac{5}{3}$ प्राप्त होता है और इससे हम निष्कर्ष निकालते हैं कि $\frac{-7}{5}>\frac{-5}{3}$ है। ऐसे पाँच युग्म और लीजिए और फिर उनकी तुलना कीजिए। कौन बड़ा है : $-\frac{3}{8}$ या $-\frac{2}{7}?;-\frac{4}{3}$ या $-\frac{3}{2}$ ?

$\bullet$ एक ॠणात्मक और धनात्मक परिमेय संख्या की तुलना सुस्पष्ट है। संख्या रेखा पर, एक ॠणात्मक परिमेय संख्या शून्य के बाईं ओर स्थित होती है तथा एक धनात्मक परिमेय संख्या शून्य के दाईं ओर स्थित होती है। अतः, एक ॠणात्मक परिमेय संख्या सदैव एक धनात्मक परिमेय संख्या से छोटी होती है।

इस प्रकार $-\frac{2}{7}<\frac{1}{2}$ है।

$\bullet$ परिमेय संख्याओं $\frac{-3}{-5}$ और $\frac{-2}{-7}$ की तुलना करने के लिए पहले उन्हें मानक रूप में बदलिए और फिर उनकी तुलना कीजिए।

उदाहरण 3 क्या $\frac{4}{-9}$ और $\frac{-16}{36}$ एक ही परिमेय संख्या को निरूपित करते हैं?

हल

$\text{ हाँ, क्योंकि }\frac{4}{-9}=\frac{4\times (-4)}{-9\times (-4)}=\frac{-16}{36}\text{ या }\frac{-16}{36}=\frac{-16÷-4}{36÷-4}=\frac{4}{-9}\text{ है। }$

8.8 दो परिमेय संख्याओं के बीच में परिमेय संख्याएँ

रेशमा $3$ और $10$ के बीच में पूर्ण संख्याएँ गिनना चाहती थी। उसको अपनी पिछली कक्षाओं से यह ज्ञात था कि $3$ और $10$ के बीच में ठीक $6$ पूर्ण संख्याएँ होंगी। इसी प्रकार, वह $-3$ और $3$ के बीच पूर्णांकों की संख्या भी ज्ञात करना चाहती थी। $-3$ और $3$ के बीच में पूर्णांक $-2,-1,0,1$ और $2$ हैं। इस प्रकार, $-3$ और $3$ के बीच ठीक $5$ पूर्णांक हैं।

क्या $-3$ और $-2$ के बीच कोई पूर्णांक हैं? नहीं, $-3$ और $-2$ के बीच कोई पूर्णांक नहीं है। दो क्रमागत पूर्णांकों के बीच पूर्णांकों की संख्या $0$ होती है।

इस प्रकार, हम प्राप्त करते हैं कि दो पूर्णांकों के बीच में पूर्णांकों की संख्या सीमित परिमित या (finite) होती है।

क्या यह परिमेय संख्याओं की स्थिति में भी होगा?

रेशमा ने दो परिमेय संख्याएँ $\frac{-3}{5}$ और $\frac{-1}{3}$ लीं।

उसने इन्हें समान हर वाली परिमेय संख्याओं में बदल लिया।

अत: $\frac{-3}{5}=\frac{-9}{15}\text{ और }\frac{-1}{3}=\frac{-5}{15}\text{ है। }$

हमें प्राप्त है कि $\frac{-9}{15}<\frac{-8}{15}<\frac{-7}{15}<\frac{-6}{15}<\frac{-5}{15}$ है, या $\frac{-3}{5}<\frac{-8}{15}<\frac{-7}{15}<\frac{-6}{15}<\frac{-1}{3}$ है।

इस प्रकार, वह $\frac{-3}{5}$ और $\frac{-1}{3}$ के बीच में परिमेय संख्याएँ $\frac{-8}{15},\frac{-7}{15},\frac{-6}{15}$ ज्ञात कर सकी।

क्या $\frac{-3}{5}$ और $\frac{-1}{3}$ के बीच में केवल परिमेय संख्याएँ $\frac{-8}{15},\frac{-7}{15},\frac{-6}{15}$ ही हैं?

हमें प्राप्त है कि $\frac{-3}{5}=\frac{-18}{30}$ और $\frac{-3}{15}=\frac{-16}{30}$ है।

साथ ही, $\frac{-18}{30}<\frac{-17}{30}<\frac{-16}{30}$ है। अर्थात् $\frac{-3}{5}<\frac{-17}{30}<\frac{-8}{15}$ है।

अत: $\frac{-3}{5}<\frac{-17}{30}<\frac{-8}{15}<\frac{-7}{15}<\frac{-6}{15}<\frac{-1}{3}\text{ है। }$

इस प्रकार, $\frac{-1}{3}$ और $\frac{-3}{5}$ के बीच हम एक और परिमेय संख्या ज्ञात करने में सफल हो गए। इस विधि का प्रयोग करके, आप दो भिन्न-भिन्न परिमेय संख्याओं के बीच में जितनी चाहें उतनी परिमेय संख्याएँ ज्ञात कर सकते हैं।

प्रयास कीजिए

$\frac{-5}{7}$ और $\frac{-3}{8}$ के बीच में पाँच परिमेय संख्याएँ ज्ञात कीजिए।

उदाहरणार्थ,

$\frac{-3}{5}=\frac{-3\times 30}{5\times 30}=\frac{-90}{150}\text{ और }\frac{-1}{3}=\frac{-1\times 50}{3\times 50}=\frac{-50}{150}\text{ है। }$

हमें $\frac{-90}{150}$ और $\frac{-50}{150}$ के बीच में, अर्थात् $\frac{-3}{5}$ और $\frac{-1}{3}$ के बीच में 39

परिमेय संख्याएँ $\frac{-89}{150},\frac{-88}{150},\frac{-87}{150},\dots ,\frac{-51}{150}$ प्राप्त करते हैं।

आप यह ज्ञात करेंगे कि यह सूची कभी समाप्त नहीं होगी। क्या आप $\frac{-5}{3}$ और $\frac{-8}{7}$ के बीच में पाँच परिमेय संख्याएँ लिख सकते हैं? हम दो परिमेय संख्याओं के बीच में असीमित (या अपरिमित रूप से अनेक) परिमेय संख्याएँ ज्ञात कर सकते हैं।

उदाहरण 4 $-2$ और -1 के बीच में तीन परिमेय संख्याएँ लिखिए।

हल

आइए $-1$ और $-2$ को हर $5$ वाली परिमेय संख्याओं के रूप में लिखें।

हमें प्राप्त है कि $-1=\frac{-5}{5}$ और $-2=\frac{-10}{5}$ है।

अतः $\frac{-10}{5}<\frac{-9}{5}<\frac{-8}{5}<\frac{-7}{5}<\frac{-6}{5}<\frac{-5}{5}$ है, या $-2<\frac{-9}{5}<\frac{-8}{5}<\frac{-7}{5}<\frac{-6}{5}<-1$ है।

$-2$ और $-1$ के बीच तीन परिमेय संख्याएँ $\frac{-9}{5},\frac{-8}{5},\frac{-7}{5}$ होंगी।

(आप $\frac{-9}{5},\frac{-8}{5},\frac{-7}{5}$ और $\frac{-6}{5}$ में से कोई सी भी तीन परिमेय संख्याएँ ले सकते हैं।)

उदाहरण 5 निम्नलिखित प्रतिरूप (Pattern) में, चार और संख्याएँ लिखिए :

$\frac{-1}{3},\frac{-2}{6},\frac{-3}{9},\frac{-4}{12},\dots$

हल हमें प्राप्त है :

$\frac{-2}{6}=\frac{-1\times 2}{3\times 2},\frac{-3}{9}=\frac{-1\times 3}{3\times 3},\frac{-4}{12}=\frac{-1\times 4}{3\times 4}$

अथवा $\frac{-1\times 1}{3\times 1}=\frac{-1}{3},\frac{-1\times 2}{3\times 2}=\frac{-2}{6},\frac{-1\times 3}{3\times 3}=\frac{-3}{9},\frac{-1\times 4}{3\times 4}=\frac{-4}{12}\text{ है। }$

इस प्रकार, इन संख्याओं में हम एक प्रतिरूप देखते हैं।

अन्य संख्याएँ $\frac{-1\times 5}{3\times 5}=\frac{-5}{15},\frac{-1\times 6}{3\times 6}=\frac{-6}{18},\frac{-1\times 7}{3\times 7}=\frac{-7}{21}$ होंगी।

प्रश्नावली 8.1

1. निम्नलिखित परिमेय संख्याओं के बीच में पाँच परिमेय संख्याएँ लिखिए :

(i) $-1और0$

(ii) $-2और-1$

(iii) $\frac{-4}{5}$ और $\frac{-2}{3}$

(iv) $-\frac{1}{2}$ और $\frac{2}{3}$

2. निम्नलिखित प्रतिरूपों में से प्रत्येक में चार और परिमेय संख्याएँ लिखिए :

(i) $\frac{-3}{5},\frac{-6}{10},\frac{-9}{15},\frac{-12}{20},\dots$.

(ii) $\frac{-1}{4},\frac{-2}{8},\frac{-3}{12},\dots$.

(iii) $\frac{-1}{6},\frac{2}{-12},\frac{3}{-18},\frac{4}{-24},\dots$.

(iv) $\frac{-2}{3},\frac{2}{-3},\frac{4}{-6},\frac{6}{-9},\dots .$.

3. निम्नलिखित के समतुल्य चार परिमेय संख्याएँ लिखिए :

(i) $\frac{-2}{7}$

(ii) $\frac{5}{-3}$

(iii) $\frac{4}{9}$

4. एक संख्या रेखा खींचिए और उस पर निम्नलिखित परिमेय संख्याओं को निरूपित कीजिए :

(i) $\frac{3}{4}$

(ii) $\frac{-5}{8}$

(iii) $\frac{-7}{4}$

(iv) $\frac{7}{8}$

5. एक संख्या रेखा पर बिंदु $\mathrm{P},\mathrm{Q},\mathrm{R},\mathrm{S},\mathrm{T},\mathrm{U},\mathrm{A}$ और $\mathrm{B}$ इस प्रकार हैं कि $\mathrm{TR}=\mathrm{RS}=\mathrm{SU}$ तथा $\mathrm{AP}=\mathrm{PQ}=\mathrm{QB}$ है। $\mathrm{P},\mathrm{Q},\mathrm{R}$ और $\mathrm{S}$ से निरूपित परिमेय संख्याओं को लिखिए।

6. निम्नलिखित में से कौन-से युग्म एक ही परिमेय संख्या को निरूपित करते हैं?

(i) $\frac{-7}{21}$ और $\frac{3}{9}$

(ii) $\frac{-16}{20}$ और $\frac{20}{-25}$

(iii) $\frac{-2}{-3}$ और $\frac{2}{3}$

(iv) $\frac{-3}{5}$ और $\frac{-12}{20}$

(v) $\frac{8}{-5}$ और $\frac{-24}{15}$

(vi) $\frac{1}{3}$ और $\frac{-1}{9}$

(vii) $\frac{-5}{-9}$ और $\frac{5}{-9}$

7. निम्नलिखित परिमेय संख्याओं को उनके सरलतम रूप में लिखिए :

(i) $\frac{-8}{6}$

(ii) $\frac{25}{45}$

(iii) $\frac{-44}{72}$

(iv) $\frac{-8}{10}$

8. संकेतों $>,<$, और $=$ में से सही संकेत चुन कर रिक्त स्थानों को भरिए :

(i) $\frac{-5}{7}◻\frac{2}{3}$

(ii) $\frac{-4}{5}◻\frac{-5}{7}$

(iii) $\frac{-7}{8}◻\frac{14}{-16}$

(iv) $\frac{-8}{5}◻\frac{-7}{4}$

(v) $\frac{1}{-3}◻\frac{-1}{4}$

(vi) $\frac{5}{-11}◻\frac{-5}{11}$

(vii) $0◻\frac{-7}{6}$

9. निम्नलिखित में प्रत्येक में से कौन-सी संख्या बड़ी है?

(i) $\frac{2}{3},\frac{5}{2}$

(ii) $\frac{-5}{6},\frac{-4}{3}$

(iii) $\frac{-3}{4},\frac{2}{-3}$

(iv) $\frac{-1}{4},\frac{1}{4}$

(v) $-3\frac{2}{7},-3\frac{4}{5}$

10. निम्नलिखित परिमेय संख्याओं को आरोही क्रम में लिखिए :

(i) $\frac{-3}{5},\frac{-2}{5},\frac{-1}{5}$

(ii) $\frac{1}{3},\frac{-2}{9},\frac{-4}{3}$

(iii) $\frac{-3}{7},\frac{-3}{2},\frac{-3}{4}$

8.9 परिमेय संख्याओं पर संक्रियाएँ

आप जानते हैं कि पूर्णांकों तथा भिन्नों को किस प्रकार जोड़ा, घटाया, गुणा और भाग किया जाता है। आइए इन आधारभूत संक्रियाओं का परिमेय संख्याओं पर अध्ययन करें।

8.9.1 योग

$\bullet$ आइए समान हर वाली दो परिमेय संख्याओं, मान लीजिए $\frac{7}{3}$ और $\frac{-5}{3}$, को जोड़ें।

हम $\frac{7}{3}+\left(\frac{-5}{3}\right)$ ज्ञात करते हैं।

संख्या रेखा पर, हमें प्राप्त होता है :

दो क्रमागत बिंदुओं के बीच की दूरी $\frac{1}{3}$ है। अतः, $\frac{7}{3}$ में $\frac{-5}{3}$ जोड़ने का अर्थ है कि $\frac{7}{3}$ के

बाईं ओर 5 कदम चलें। हम कहाँ पहुँचते हैं? हम $\frac{2}{3}$ पर पहुँचते हैं। अतः $\frac{7}{3}+\left(\frac{-5}{3}\right)=\frac{2}{3}$ है। आइए इसको इस प्रकार करने का प्रयत्न करें :

$\frac{7}{3}+\frac{(-5)}{3}=\frac{7+(-5)}{3}=\frac{2}{3}$

हमें वही उत्तर प्राप्त होता है।

$\frac{6}{5}+\frac{(-2)}{5},\frac{3}{7}+\frac{(-5)}{7}$ को उपरोक्त दोनों विधियों से ज्ञात कीजिए और जाँच करें कि क्या दोनों उत्तर समान हैं। इसी प्रकार, $\frac{-7}{8}+\frac{5}{8}$ निम्नलिखित होगा :

हमें क्या प्राप्त होता है?

साथ ही, $\frac{-7}{8}+\frac{5}{8}=\frac{-7+5}{8}=$ ? क्या दोंनों मान समान हैं?

प्रयास कीजिए

$\frac{-13}{7}+\frac{6}{7}\text{ तथा }\frac{19}{5}+\left(\frac{-7}{5}\right)\text{ ज्ञात कीजिए: }$

इस प्रकार, हम देखते हैं कि समान हर वाली परिमेय संख्याओं को जोड़ते समय, हम, हर को वही रखते हुए, अंशों को जोड़ देते हैं।

इस प्रकार, $\frac{-11}{5}+\frac{7}{5}=\frac{-11+7}{5}=\frac{-4}{5}$ है।

$\bullet$ हम अलग-अलग हरों वाली दो परिमेय संख्याओं को किस प्रकार जोडेें? भिन्नों की तरह, हम पहले इन हरों का ल.स. ज्ञात करते हैं। फिर हम ऐसी समतुल्य परिमेय संख्याएँ ज्ञात करते हैं, जिनके हर यह ल.स. हों। इसके बाद हम इन दोनों परिमेय संख्याओं को जोड़ते हैं।

उदाहरणार्थ, आइए $\frac{-7}{5}$ और $\frac{-2}{3}$ को जोड़ें। $5$ और $3$ का ल.स. $15$ है।

अत: $\frac{-7}{5}=\frac{-21}{15}$ और $\frac{-2}{3}=\frac{-10}{15}$ है।

इस प्रकार $\frac{-7}{5}+\left(\frac{-2}{3}\right)=\frac{-21}{15}+\left(\frac{-10}{15}\right)=\frac{-31}{15}$ हुआ।

योज्य प्रतिलोम :

$\frac{-4}{7}+\frac{4}{7}$ किसके बराबर होगा?

$\frac{-4}{7}+\frac{4}{7}=\frac{-4+4}{7}=0$ है। साथ ही, $\frac{4}{7}+\left(\frac{-4}{7}\right)=0$ है

इसी प्रकार, $\frac{-2}{3}+\frac{2}{3}=0=\frac{2}{3}+\left(\frac{-2}{3}\right)$ है। ज्ञात कीजिए :

प्रयास कीजिए

(i) $\frac{-3}{7}+\frac{2}{3}$

(ii) $\frac{-5}{6}+\frac{-3}{11}$

आपको याद होगा कि पूर्णांकों में, $-2$ का योज्य प्रतिलोम (additive inverse) $2$ है, तथा $2$ , पूर्णांक $-2$ का योज्य प्रतिलोम होता है।

परिमेय संख्याओं के लिए, हम कहते हैं कि $\frac{-4}{7}$ परिमेय संख्या $\frac{4}{7}$

का योज्य प्रतिलोम है तथा $\frac{4}{7}$ परिमेय संख्या $\frac{-4}{7}$ का योज्य प्रतिलोम है।

इसी प्रकार, $\frac{-2}{3}$ परिमेय संख्या $\frac{2}{3}$ का योज्य प्रतिलोम है तथा $\frac{2}{3}$ परिमेय संख्या $\frac{-2}{3}$ का योज्य प्रतिलोम है।

प्रयास कीजिए

$\frac{-3}{9},\frac{-9}{11}$ और $\frac{5}{7}$ के योज्य प्रतिलोम क्या हैं?

उदाहरण 6 सतपाल किसी स्थान $\mathrm{P}$ से पूर्व दिशा में $\frac{2}{3}\mathrm{km}$ चलता है और फिर वहाँ से पश्चिम दिशा में $1\frac{5}{7}\mathrm{km}$ चलता है। अब वह $\mathrm{P}$ से कहाँ स्थित होगा?

हल आइए पूर्व दिशा में चली गई दूरी को धनात्मक चिह्न से व्यक्त करें। इसलिए, पश्चिम दिशा में चली गई दूरी को ॠणात्मक चिह्न से व्यक्त किया जाएगा।

इस प्रकार, बिंदु $\mathrm{P}$ से सतपाल की दूरी ( $\mathrm{km}$ में) होगी :

$\frac{2}{3}+(-1\frac{5}{7})=\frac{2}{3}+\frac{(-12)}{7}=\frac{2\times 7}{3\times 7}+\frac{(-12)\times 3}{7\times 3}$

$=\frac{14-36}{21}=\frac{-22}{21}=-1\frac{1}{21}$

क्योंकि यह ॠणात्मक है, इसलिए सतपाल $\mathrm{P}$ से पश्चिम की ओर $1\frac{1}{21}\mathrm{km}$ की दूरी पर है।

8.9.2 व्यवकलन ( घटाना )

सविता ने दो परिमेय संख्याओं $\frac{5}{7}$ और $\frac{3}{8}$ का अंतर इस विधि से प्राप्त किया :

$\frac{5}{7}-\frac{3}{8}=\frac{40-21}{56}=\frac{19}{56}$

फरीदा जानती थी कि दो पूर्णांकों $a$ और $b$ के लिए, $a-b=a+(-b)$ लिखा जा सकता है।

उसने ऐसा परिमेय संख्याओं के लिए भी किया और ज्ञात किया कि $\frac{5}{7}-\frac{3}{8}=\frac{5}{7}+\frac{(-3)}{8}=\frac{19}{56}$ है। दोनों ने एक ही (समान) अंतर प्राप्त किया।

दोनों विधियों से, $\frac{7}{8}-\frac{5}{9},\frac{3}{11}-\frac{8}{7}$ ज्ञात करने का प्रयत्न कीजिए। क्या आपको समान उत्तर प्राप्त होते हैं?

अतः हम कहते हैं कि दो परिमेय संख्याओं को घटाते (व्यवकलन करते) समय, घटाए जाने वाली संख्या के योज्य प्रतिलोम को अन्य परिमेय संख्या में जोड़ देना चाहिए।

इस प्रकार, $1\frac{2}{3}-2\frac{4}{5}=\frac{5}{3}-\frac{14}{5}=\frac{5}{3}+\frac{14}{5}$ का योज्य प्रतिलोम

$=\frac{5}{3}+\frac{(-14)}{5}=\frac{-17}{15}=-1\frac{2}{15}\text{ है। }$

$\frac{2}{7}-\left(\frac{-5}{6}\right)$ क्या होगा? $\frac{2}{7}-\left(\frac{-5}{6}\right)=\frac{2}{7}+\left(\frac{-5}{6}\right)$ का योज्य प्रतिलोम

$=\frac{2}{7}+\frac{5}{6}=\frac{47}{42}=1\frac{5}{42}$

8.9.3 गुणन

आइए परिमेय संख्या $\frac{-3}{5}$ को 2 से गुणा करें, अर्थात् हम $\frac{-3}{5}\times 2$ ज्ञात करें।

संख्या रेखा पर इसका अर्थ होगा $\frac{3}{5}$ कि बाईं ओर दो कदम चलना।

हम कहाँ पहुँचते हैं? हम $\frac{-6}{5}$ पर पहुँचते हैं। आइए हम इसको भिन्नों वाली विधि से ज्ञात करें।

$\frac{-3}{5}\times 2=\frac{-3\times 2}{5}=\frac{-6}{5}$

हम उसी परिमेय संख्या पर पहुँच जाते हैं।

दोनों विधियों का प्रयोग करते हुए, $\frac{-4}{7}\times 3$ और $\frac{-6}{5}\times 4$, को ज्ञात कीजिए। आप क्या देखते हैं?

अतः, हम ज्ञात करते हैं कि एक परिमेय संख्या को एक धनात्मक पूर्णांक से गुणा करने पर, हम अंश को उस पूर्णांक से गुणा कर देते हैं तथा हर को वही रखते हैं।

आइए अब एक परिमेय संख्या को एक ॠणात्मक पूर्णांक से गुणा करें।

$\frac{-2}{9}\times (-5)=\frac{-2\times (-5)}{9}=\frac{10}{9}$

याद रखिए कि -5 को $\frac{-5}{1}$ लिखा जा सकता है।

अतः, $\frac{-2}{9}\times \frac{-5}{1}=\frac{10}{9}=\frac{-2\times (-5)}{9\times 1}$ है।

इसी प्रकार, $\frac{3}{11}\times (-2)=\frac{3\times (-2)}{11\times 1}=\frac{-6}{11}$ है।

प्रयास कीजिए

निम्नलिखित गुणनफल क्या होंगे?

(i) $\frac{-3}{5}\times 7$

(ii) $\frac{-6}{5}\times (-2)$

उपरोक्त प्रेक्षणों के आधार पर, हम ज्ञात करते हैं कि $\frac{-3}{8}\times \frac{5}{7}=\frac{-3\times 5}{8\times 7}=\frac{-15}{56}$ है।

अतः, जैसा कि हमने भिन्नों की स्थिति में किया था, हम दो परिमेय संख्याओं को निम्नलिखित विधि से गुणा करते हैं :

प्रयास कीजिए

ज्ञात कीजिए :

(i) $\frac{-3}{4}\times \frac{1}{7}$

(ii) $\frac{2}{3}\times \frac{-5}{9}$ चरण 2 : दोनों परिमेय संख्याओं के हरों का गुणा कीजिए।

चरण 1 : दोनों परिमेय संख्याओं के अंशों का गुणा कीजिए।

चरण 2: दोनों परिमेय संख्याओं के हरों का गुणा कीजिए। इस प्रकार,

चरण 3: $\text{ : गुणनफल को }\frac{\text{ चरण }1\text{ में प्राप्त परिणाम }}{\text{ चरण }2\text{ में प्राप्त परिणाम }}\text{ के रूप में लिखिए। }$

$\frac{-3}{5}\times \frac{2}{7}=\frac{-3\times 2}{5\times 7}=\frac{-6}{35}$ है।

साथ ही $\frac{-5}{8}\times \left(\frac{-9}{7}\right)=\frac{(-5)\times (-9)}{8\times 7}=\frac{45}{56}$ है।

8.9.4 विभाजन

भिन्नों के व्युत्क्रमों (reciprocals) के बारे में हम पहले पढ़ चुके हैं। $\frac{2}{7}$ का व्युत्क्रम क्या है?

यह $\frac{7}{2}$ है। हम इस अवधारणा को शून्येतर परिमेय संख्याओं के व्युत्क्रमों के लिए भी लागू करते हैं।

इस प्रकार, $\frac{-2}{7}$ का व्युत्क्रम $\frac{7}{-2}$, अर्थात् $\frac{-7}{2}$ होगा तथा $\frac{-3}{5}$ का व्युत्क्रम $\frac{-5}{3}$ होगा।

परिमेय संख्या का उसके व्युत्क्रम से गुणनफल

किसी संख्या का उसके व्युत्क्रम से गुणनफल सदैव 1 होता है।

उदाहरणार्थ $\frac{-4}{9}\times (\frac{-4}{9}$ का व्युत्क्रम $)$

$=\frac{-4}{9}\times \left(\frac{-9}{4}\right)=1\text{ है। }$

इसी प्रकार $\frac{-6}{13}\left(\frac{-13}{6}\right)=1$ है।

कुछ और उदाहरण लेकर, इस प्रेक्षण की पुष्टि कीजिए।

सविता ने एक परिमेय संख्या $\frac{4}{9}$ को एक अन्य परिमेय संख्या $\frac{-5}{7}$ से इस प्रकार विभाजित किया

(भाग दिया) :

$\frac{4}{9}÷\left(\frac{-5}{7}\right)=\frac{4}{9}\times \frac{7}{-5}=\frac{-28}{45}$

उसने भिन्नों की तरह ही व्युत्क्रम की अवधारणा का प्रयोग किया।

अर्पित ने पहले $\frac{4}{9}$ को $\frac{5}{7}$ से भाग दिया और $\frac{28}{45}$ प्राप्त किया।

अंत में, उसने कहा कि $\frac{4}{9}÷\left(\frac{-5}{7}\right)=\frac{-28}{45}$ है। उसने ऐसा किस प्रकार प्राप्त किया?

उसने ॠणात्मक चिद्न को छोड़ते हुए, उन्हें भिन्नों की तरह विभाजित किया और बाद में प्राप्त परिणाम के साथ ॠणात्मक चिह्न लगा दिया।

दोनों ने एक ही मान $\frac{-28}{45}$ प्राप्त किया। $\frac{2}{3}$ को $\frac{-5}{7}$ से दोनों विधियों द्वारा भाग देकर देखिए कि क्या आप एक ही (समान) उत्तर प्राप्त करते हैं।

उपरोक्त से यह प्रदर्शित होता है कि एक परिमेय संख्या को किसी अन्य परिमेय संख्या से भाग देने के लिए, हम उस परिमेय संख्या को अन्य परिमेय संख्या के व्युत्क्रम से गुणा कर देते हैं।

इस प्रकार, $\frac{6}{-5}÷\frac{-2}{3}=\frac{6}{-5}\times \left(\frac{-2}{3}\right)$ का व्युत्क्रम $=\frac{6}{-5}\times \frac{3}{-2}=\frac{18}{10}$ है।

प्रयास कीजिए

ज्ञात कीजिए: (i) $\frac{2}{3}\times \left(\frac{-7}{8}\right)$ (ii) $\frac{-6}{7}\times \frac{5}{7}$

प्रश्नावली 8.2

1. योग ज्ञात कीजिए :

(i) $\frac{5}{4}+\left(\frac{-11}{4}\right)$

(ii) $\frac{5}{3}+\frac{3}{5}$

(iii) $\frac{-9}{10}+\frac{22}{15}$

(iv) $\frac{-3}{-11}+\frac{5}{9}$

(v) $\frac{-8}{19}+\frac{(-2)}{57}$

(vi) $\frac{-2}{3}+0$

(vii) $-2\frac{1}{3}+4\frac{3}{5}$

2. ज्ञात कीजिए :

(i) $\frac{7}{24}-\frac{17}{36}$

(ii) $\frac{5}{63}-\left(\frac{-6}{21}\right)$

(iii) $\frac{-6}{13}-\left(\frac{-7}{15}\right)$

(iv) $\frac{-3}{8}-\frac{7}{11}$

(v) $-2\frac{1}{9}-6$

3. गुणनफल ज्ञात कीजिए :

(i) $\frac{9}{2}\times \left(\frac{-7}{4}\right)$

(ii) $\frac{3}{10}\times (-9)$

(iii) $\frac{-6}{5}\times \frac{9}{11}$

(iv) $\frac{3}{7}\times \left(\frac{-2}{5}\right)$

(v) $\frac{3}{11}\times \frac{2}{5}$

(vi) $\frac{3}{-5}\times \frac{-5}{3}$

4. निम्नलिखित के मान ज्ञात कीजिए :

(i) $(-4)÷\frac{2}{3}$

(ii) $\frac{-3}{5}÷2$

(iii) $\frac{-4}{5}÷(-3)$

(iv) $\frac{-1}{8}÷\frac{3}{4}$

(v) $\frac{-2}{13}÷\frac{1}{7}$

(vi) $\frac{-7}{12}÷\left(\frac{-2}{13}\right)$

(vii) $\frac{3}{13}÷\left(\frac{-4}{65}\right)$

हमने क्या चर्चा की?

1. एक संख्या जिसे $\frac{p}{q}$ के रूप में व्यक्त किया जा सके, जहाँ $p$ और $q$ पूर्णांक हैं तथा $q\ne 0$ है,

परिमेय संख्या कहलाती है। संख्याएँ $\frac{-2}{7},\frac{3}{8},3$ इत्यादि परिमेय संख्याएँ हैं।

2. सभी पूर्णांक और भिन्न परिमेय संख्याएँ हैं।

3. यदि किसी परिमेय संख्या के अंश और हर को एक ही शून्येतर पूर्णांक से गुणा किया जाए या भाग दिया जाए, तो हमें एक परिमेय संख्या प्राप्त होती है जो दी हुई परिमेय संख्या के समतुल्य परिमेय संख्या कही जाती है।

उदाहरणार्थ, $\frac{-3}{7}=\frac{-3\times 2}{7\times 2}=\frac{-6}{14}$ है।

अतः, हम कहते हैं कि $\frac{-6}{14}$ संख्या $\frac{-3}{7}$ का एक समतुल्य रूप है। साथ ही,

ध्यान दीजिए कि $\frac{-6}{14}=\frac{-6÷2}{14÷2}=\frac{-3}{7}$ है।

4. परिमेय संख्याओं को धनात्मक और ॠणात्मक परिमेय संख्याओं के रूप में वर्गीकृत किया जाता है। जब अंश और हर दोनों ही या तो धनात्मक पूर्णांक हों या ॠणात्मक पूर्णांक हों, तो वह परिमेय संख्या धनात्मक परिमेय संख्या कहलाती है। जब अंश या हर में से एक ॠणात्मक पूर्णांक हो, तो वह परिमेय संख्या एक ॠणात्मक परिमेय संख्या कहलाती है।

उदाहरणार्थ, $\frac{3}{8}$ एक धनात्मक परिमेय संख्या है तथा $\frac{-8}{9}$ एक ॠणात्मक परिमेय संख्या है।

5. संख्या 0 न तो एक धनात्मक परिमेय संख्या है और न ही ॠणात्मक परिमेय संख्या है।

6. एक परिमेय संख्या को अपने मानक रूप में तब माना जाता है, जब उसका हर धनात्मक पूर्णांक हो तथा अंश और हर में $1$ के अतिरिक्त कोई सार्व गुणनखंड न हो। संख्याएँ $\frac{-1}{3},\frac{2}{7}$, इत्यादि मानक रूप में हैं।

7. दो परिमेय संख्याओं के बीच असीमित परिमेय संख्याएँ होती हैं।

8. समान हर वाली दो परिमेय संख्याओं का योग ज्ञात करने के लिए, उनके अंशों को जोड़ा जा सकता है तथा हर वही रख कर योग ज्ञात किया जा सकता है। भिन्न-भिन्न हरों वाली दो परिमेय संख्याओं को जोड़ने के लिए, पहले दोनों हरों का ल.स. ज्ञात किया जाता है और फिर दोनों परिमेय संख्याओं को ल.स. के बराबर समान हर वाली दो समतुल्य परिमेय संख्याओं में बदल कर जोड़ लिया जाता है।

उदाहरणार्थ, $\frac{-2}{3}+\frac{3}{8}=\frac{-16}{24}+\frac{9}{24}=\frac{-16+9}{24}=\frac{-7}{24}$ है। यहां 3 और 8 का ल. स. 24 है।

9. दो परिमेय संख्याओं का व्यवकलन करने के लिए हम घटाई जाने वाली परिमेय संख्या के योज्य प्रतिलोम को अन्य परिमेय संख्या में जोड़ते हैं।

इस प्रकार, $\frac{7}{8}-\frac{2}{3}=\frac{7}{8}+\frac{2}{3}$ का योज्य प्रतिलोम $=\frac{7}{8}+\frac{(-2)}{3}=\frac{21+(-16)}{24}=\frac{5}{24}$ है।

10. दो परिमेय संख्याओं का गुणा करने के लिए, हम इन संख्याओं के अंशों तथा हरों को अलग-अलग गुणा करते हैं

और फिर गुणनफल को $\frac{\text{ अंशों का गुणनफल }}{\text{ हरों का गुणनफल }}$ के रूप में लिखते हैं।

11. एक परिमेय संख्या को एक अन्य शून्येतर परिमेय संख्या से भाग देने के लिए, हम पहली परिमेय संख्या को अन्य परिमेय संख्या के व्युत्क्रम से गुणा करते हैं।

इस प्रकार $\frac{-7}{2}÷\frac{4}{3}=\frac{-7}{2}\times (\frac{4}{3}$ का व्युत्क्रम $)=\frac{-7}{2}\times \frac{3}{4}=\frac{-21}{8}$ है।