6.1 भूमिका

आप देख चुके हैं कि त्रिभुज, तीन रेखाखंडों से बनी एक बंद सरल आकृति है। इसके तीन शीर्ष, तीन भुजाएँ व तीन कोण होते हैं। यहाँ एक $\triangle \mathrm{ABC}$ (आकृति 6.1) है। इसमें हैं :

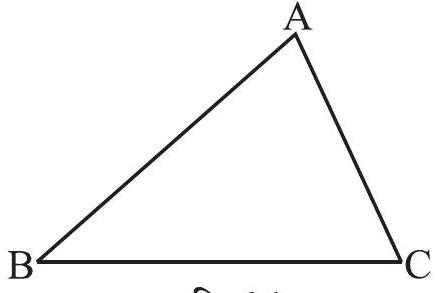
आकृति 6.1

भुजाएँ : $\quad \overline{\mathrm{AB}}, \overline{\mathrm{BC}}, \overline{\mathrm{CA}} $

कोण : $\quad \angle \mathrm{BAC}, \angle \mathrm{ABC}, \angle \mathrm{BCA}$

शीर्ष : $\quad A, B, C$

शीर्ष $\mathrm{A}$ की सम्मुख भुजा $\overline{\mathrm{BC}}$ है। क्या आप भुजा $\overline{\mathrm{AB}}$ के सम्मुख कोण का नाम बता सकते हैं ? आप जानते हैं कि त्रिभुजों का वर्गीकरण (i) भुजाओं (ii) कोणों के आधार पर किस प्रकार किया जाता है।

(i) भुजाओं के आधार पर : विषमबाहु, समद्विबाहु तथा समबाहु त्रिभुज ।

(ii) कोणों के आधार पर : न्यून कोण, अधिक कोण तथा समकोण त्रिभुज।

ऊपर बताए गए, सभी प्रकार के त्रिभुजों के आकारों के नमूने, कागज़ से काटकर बनाइए। अपने नमूनों की, साथियों के नमूनों से तुलना कीजिए और उनके बारे में चर्चा कीजिए।

प्रयास कीजिए

1. $\triangle \mathrm{ABC}$ के छः अवयवों (तीन भुजाओं तथा तीन कोणों) के नाम लिखिए।

2. लिखिए:

(i) $\triangle \mathrm{PQR}$ के शीर्ष $\mathrm{Q}$ की सम्मुख भुजा

(ii) $\triangle \mathrm{LMN}$ की भुजा $\mathrm{LM}$ का सम्मुख कोण

(iii) $\triangle \mathrm{RST}$ की भुजा $\mathrm{RT}$ का सम्मुख शीर्ष

3. आकृति 6.2 देखिए तथा त्रिभुजों में से प्रत्येक का वर्गीकरण कीजिए :

(a) भुजाओं के आधार पर

(b) कोणों के आधार पर

आकृति 6.2

आइए, त्रिभुजों के बारे में कुछ और अधिक जानने का प्रयास करें।

6.2 त्रिभुज की माध्यिकाएँ

आप जानते हैं कि एक दिए गए रेखाखंड का लंब समद्विभाजक कागज़ मोड़ने की प्रक्रिया द्वारा कैसे ज्ञात किया जाता है।

कागज़ के टुकड़े से एक त्रिभुज $\mathrm{ABC}$ काटिए (आकृति 6.3)। इसकी कोई एक भुजा, मानों $\overline{\mathrm{BC}}$ लीजिए। कागज़ मोड़ने की प्रक्रिया द्वारा $\overline{\mathrm{BC}}$ का लंब समद्विभाजक ज्ञात कीजिए। कागज़ पर मोड़ की तह, भुजा $\overline{\mathrm{BC}}$ को $\mathrm{D}$ पर काटती है जो उसका मध्य बिंदु है। शीर्ष $\mathrm{A}$ को $\mathrm{D}$ से मिलाइए।

रेखाखंड $\mathrm{AD}$, जो भुजा $\overline{\mathrm{BC}}$ के मध्यबिंदु $\mathrm{D}$ को सम्मुख शीर्ष $\mathrm{A}$ से मिलाता है, त्रिभुज की एक माध्यिका है।

भुजाएँ $\overline{\mathrm{AB}}$ तथा $\overline{\mathrm{CA}}$ लेकर, इस त्रिभुज की दो और माध्यिकाएँ खींचिए। माध्यिका, त्रिभुज के एक शीर्ष को, सम्मुख भुजा के मध्य बिंदु से मिलाती है।

सोचिए, चर्चा कीजिए और लिखिए

1. एक त्रिभुज में कितनी माध्यिकाएँ हो सकती हैं ?

2. क्या एक माध्यिका पूर्णतया त्रिभुज के अंदर में स्थित होती है ? (यदि आप समझते हैं कि यह सत्य नहीं है तो उस स्थिति के लिए एक आकृति खींचिए।)

6.3 त्रिभुज के शीर्षलंब

त्रिभुज के आकार वाला गत्ते का एक टुकड़ा $\mathrm{ABC}$ लीजिए। इसे एक मेज पर सीधा ऊर्ध्वाधर खड़ा कीजिए। इसकी ऊँचाई कितनी है ? यह ऊँचाई शीर्ष $\mathrm{A}$ से भुजा $\overline{\mathrm{BC}}$ तक की दूरी है (आकृति 6.4)।

शीर्ष $\mathrm{A}$ से भुजा $\overline{\mathrm{BC}}$ तक अनेक रेखाखंड खींचे जा सकते हैं (आकृति 6.5)। इनमें से त्रिभुज की ऊँचाई कौन-सी रेखाखंड प्रदर्शित करती है ?

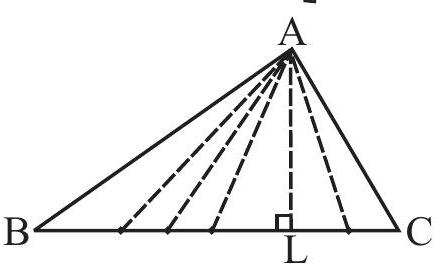
आकृति 6.5

वह रेखाखंड जो शीर्ष $\mathrm{A}$ से सीधा ऊर्ध्वाधर नीचे $\overline{\mathrm{BC}}$ तक और

उस पर लंबवत होता है, इसकी ऊँचाई होती है ।

रेखाखंड AL त्रिभुज का एक शीर्षलंब है ।

शीर्षलंब का एक अंत बिंदु, त्रिभुज के एक शीर्ष पर और दूसरा अंत बिंदु सम्मुख भुजा बनाने वाली रेखा पर स्थित होता है। प्रत्येक शीर्ष से एक शीर्षलंब खींचा जा सकता है ।

सोचिए, चर्चा कीजिए और लिखिए

1. एक त्रिभुज में कितने शीर्ष हो सकते हैं?

2. निम्न त्रिभुजों में $\mathrm{A}$ से $\overline{\mathrm{BC}}$ तक अनुमान से शीर्षलंब खींचिए। (आकृति 6.6) :

आकृति 6.6

3. क्या एक शीर्षलंब पूर्णतया त्रिभुज के अभ्यंतर में सदैव स्थित होगा ? (यदि आप समझते हैं कि यह सत्य होना आवश्यक नहीं है तो उस स्थिति के लिए एक आकृति खींचिए।

4. क्या आप कोई ऐसा त्रिभुज सोच सकते हैं; जिसके दो शीर्षलंब उसकी दो भुजाएँ ही हों ?

5. क्या किसी त्रिभुज की माध्यिका व शीर्षलंब एक ही रेखाखंड हो सकता है ?

(संकेतः प्रश्न 4 व 5 के लिए, प्रत्येक प्रकार के त्रिभुज के शीर्षलंब खींचकर खोज करिए।)

कागज़ से काटी गई इन आकृतियों को लीजिए।

(i) समबाहु त्रिभुज

(ii) समद्विबाहु त्रिभुज तथा

(iii) विषमबाहु त्रिभुज

इनके शीर्षलंब तथा माध्यिकाएँ ज्ञात कीजिए। क्या आप इनमें कुछ विशेषता पाते हैं? अपने साथियों के साथ इन पर चर्चा कीजिए।

प्रश्नावली 6.1

1. $\triangle \mathrm{PQR}$ में भुजा $\overline{\mathrm{QR}}$ का मध्य बिंदु $\mathrm{D}$ है

$\overline{\mathrm{PM}}$ $\qquad$ __________________है।

PD $\qquad$ ___________________है ।

क्या $\mathrm{QM}=\mathrm{MR}$ ?

2. निम्न के लिए अनुमान से आकृति खींचिए।

(a) $\triangle \mathrm{ABC}$ में, $\mathrm{BE}$ एक माध्यिका है ।

(b) $\triangle \mathrm{PQR}$ में, $\mathrm{PQ}$ तथा $\mathrm{PR}$ त्रिभुज के शीर्षलंब हैं।

(c) $\triangle X Y Z$ में, $YL$ एक शीर्षलंब उसके बहिर्भाग में है ।

3. आकृति खींचकर पुष्टि कीजिए कि एक समद्विबाहु त्रिभुज में शीर्षलंब व माध्यिका एक ही रेखाखंड हो सकता है।

6.4 त्रिभुज का बाहय कोण एवं इसके गुण

इन्हें कीजिए

1. एक त्रिभुज $\mathrm{ABC}$ खींचिए और इसकी एक भुजा, $\overline{\mathrm{BC}}$ को एक ओर बढ़ाइए (आकृति 6.7)। शीर्ष $\mathrm{C}$ पर बने कोण $\mathrm{ACD}$ पर ध्यान दीजिए। यह कोण $\triangle \mathrm{ABC}$ के बहिर्भाग में स्थित है। हम इसे $\triangle \mathrm{ABC}$ के शीर्ष $\mathrm{C}$ पर बना एक बाह्य कोण कहते हैं।

आकृति 6.7

स्पष्ट है कि $\angle \mathrm{BCA}$ तथा $\angle \mathrm{ACD}$ परस्पर संलग्न कोण हैं। त्रिभुज के शेष दो कोण, $\angle \mathrm{A}$ तथा $\angle \mathrm{B}$ बाह्य कोण $\mathrm{ACD}$ के दो सम्मुख अंतःकोण या दूरस्थ अंतःकोण कहलाते हैं। अब काट कर या अक्स (Trace copy) लेकर $\angle \mathrm{A}$ तथा $\angle \mathrm{B}$ एक दूसरे के संलग्न मिलाकर $\angle \mathrm{ACD}$ पर रखिए जैसा कि आकृति 6.8 में दिखाया गया है ।

क्या ये दोनों कोण $\angle \mathrm{ACD}$ को पूर्णतया आच्छादित करते हैं ?

क्या आप कह सकते हैं

$m \angle \mathrm{ACD}=m \angle \mathrm{A}+m \angle \mathrm{B}$ ?

2. जैसा कि पहले किया गया है, एक त्रिभुज $\mathrm{ABC}$ लेकर उसका बाह्य कोण $ACD$ बनाइए। कोण मापक की सहायता से $\angle \mathrm{ACD}, \angle \mathrm{A}$ तथा $\angle \mathrm{B}$ को मापिए ।

$\angle \mathrm{A}+\angle \mathrm{B}$ का योग ज्ञात कर उसकी तुलना $\angle \mathrm{ACD}$ की माप से कीजिए। कोण मापक की सहायता से $\angle \mathrm{ACD}$ की माप $\angle \mathrm{A}+\angle \mathrm{B}$ के बराबर होगी। यदि माप में कोई त्रुटि है तो इसकी माप लगभग बराबर होगी ।

इन दो क्रियाकलापों को, कुछ अन्य त्रिभुज लेकर और उनके बाह्य कोण खींचकर, आप दोहरा सकते हैं। प्रत्येक बार आप यही पाएँगे कि त्रिभुज का बाह्य कोण उसके दोनों सम्मुख अंतःकोणों के योग के बराबर होता है ।

एक चरणबद्ध व तर्कपूर्ण विधि से भी इस गुण की पुष्टि की जा सकती है।

किसी त्रिभुज का बाहय कोण अपने दोनों सम्मुख अंतःकोणों के योग के बराबर होता है।

दिया है : $\triangle \mathrm{ABC}$ लेते हैं। $\angle \mathrm{ACD}$ इसका एक बाह्य कोण है।

दिखाना है : $m \angle \mathrm{ACD}=m \angle \mathrm{A}+m \angle \mathrm{B}$

शीर्ष $\mathrm{C}$ से भुजा $\overline{\mathrm{BA}}$ के समांतर $\mathrm{CE}$ रेखा खींचिए ।

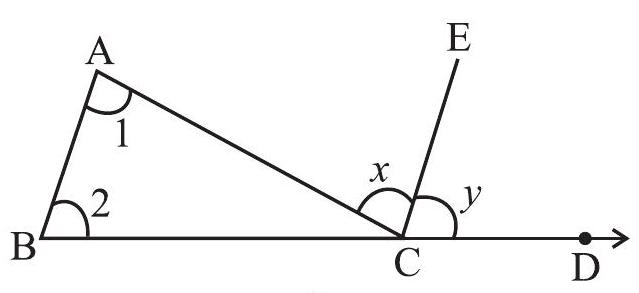
आकृति 6.9

औचित्य

किसी त्रिभुज में बाहय कोण और उसके दोनों सम्मुख अंतःकोणों के बीच यह संबंध त्रिभुज के बाहय कोण के गुण के नाम से जाना जाता है ।

सोचिए, चर्चा कीजिए और लिखिए

1. एक त्रिभुज के लिए बाहय कोण भिन्न-भिन्न प्रकार से बनाए जा सकते हैं। इनमें से तीन, निम्न प्रकार से दिखाए गए हैं (आकृति 6.10)।

आकृति 6.10

इनके अतिरिक्त तीन और प्रकार से भी बाह्य कोण बनाए जा सकते हैं। उन्हें भी अनुमान से बनाइए।

2. किसी त्रिभुज के एक शीर्ष पर बने दोनों बाह्य कोण क्या परस्पर समान होते हैं ?

3. किसी त्रिभुज के एक बाहय कोण और उसके संलग्न अंतःकोण के योग के बारे में आप क्या कह सकते हैं ?

उदाहरण 1 आकृति 6.11 में $x$ का मान ज्ञात कीजिए।

हल सम्मुख अंतःकोणों का योग $=$ बाहय कोण

अथवा $\quad 50^{\circ}+x =110^{\circ} $

अथवा $\quad x =60^{\circ}$

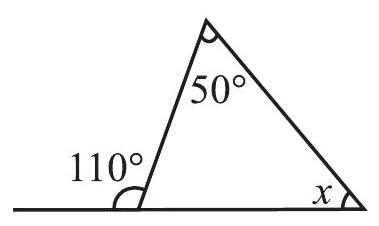
आकृति 6.11

सोचिए, चर्चा कीजिए और लिखिए

1. प्रत्येक दशा में अंतः सम्मुख कोणों के बारे में आप क्या कह सकते हैं जब कि बाहय कोण है:

(i) एक समकोण

(ii) एक अधिक कोण

(iii) एक न्यून कोण

2. क्या किसी त्रिभुज का कोई बाहय कोण एक सरल कोण भी हो सकता है ?

प्रयास कीजिए

आकृति 6.12

1. किसी त्रिभुज में एक बाह्य कोण की माप $70^{\circ}$ है और उसके अंतः सम्मुख कोणों में से एक की माप $25^{\circ}$ है। दूसरे अंतः सम्मुख कोण की माप ज्ञात कीजिए।

2. किसी त्रिभुज के दो अंतः सम्मुख कोणों की माप $60^{\circ}$ तथा $80^{\circ}$ है। उसके बाहय कोण की माप ज्ञात कीजिए।

3. क्या इस आकृति में कोई त्रुटि है (आकृति 6.12)? टिप्पणी करें।

प्रश्नावली 6.2

1. निम्न आकृतियों में अज्ञात बाहय कोण $x$ का मान ज्ञात कीजिए।

2. निम्न आकृतियों में अज्ञात अंतःकोण $x$ का मान ज्ञात कीजिए।

6.5 त्रिभुज के अंत:कोणों का योग गुण

त्रिभुज के तीनों कोणों का आपस में संबंध दर्शाने वाला एक अद्भुत गुण है। इस गुण को आप निम्नलिखित चार क्रियाकलापों द्वारा देख व समझ पाएँगे।

1. एक त्रिभुज खींचिए। इसके तीनों कोणों को काटकर अलग-अलग कीजिए। इन्हें अब इस प्रकार व्यवस्थित करके रखिए जैसा कि (i) आकृति 6.13 (i) व (ii) में दिखाया गया है ।

ये तीनों कोण मिलकर एक कोण बनाते हैं। जिसकी माप $180^{\circ}$ है। इस प्रकार, त्रिभुज के तीनों कोणों की मापों का योग $180^{\circ}$ होता है।

2. इस तथ्य को आप एक अन्य विधि द्वारा भी देख सकते हैं। किसी $\triangle \mathrm{ABC}$ के तीन प्रतिरूप बनाइए, (आकृति 6.14)।

आकृति 6.14

इन तीनों को आकृति 6.15 की भाँति मिलाकर ठीक से रखिए। $\angle 1+\angle 2+\angle 3$ के बारे में आप क्या अवलोकन करते हैं ?

(क्या आप यहाँ बाहय कोण से संबंधित गुण भी देख पाते हैं ?)

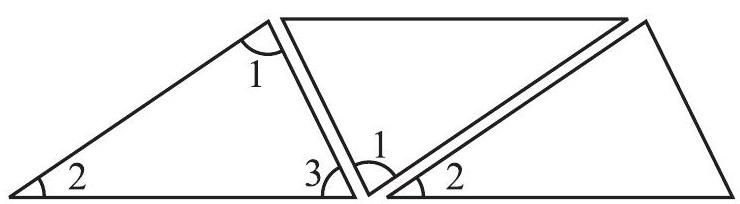
आकृति 6.15

3. कागज़ के एक टुकड़े से कोई एक त्रिभुज, जैसे $\triangle \mathrm{ABC}$ (आकृति 6.16) काटिए।

इस त्रिभुज को मोड़कर शीर्ष $A$ से गुज़रता हुआ शीर्षलंब $A M$ निर्धारित कीजिए। अब इस त्रिभुज के तीनों कोनों को इस प्रकार मोड़िए जिससे तीनों शीर्ष $\mathrm{A}, \mathrm{B}$ तथा $\mathrm{C}$ बिंदु $\mathrm{M}$ पर मिलें।

आकृति 6.16

आप देखते हैं कि त्रिभुज के तीनों कोण मिलकर एक सरल कोण बनाते हैं। यह क्रियाकलाप पुन: दर्शाता है कि त्रिभुज के तीनों कोणों की मापों का योग $180^{\circ}$ होता है ।

4. अपनी अभ्यास पुस्तिका में कोई तीन त्रिभुज, मानों $\triangle \mathrm{ABC}, \triangle \mathrm{PQR}$ तथा $\triangle \mathrm{XYZ}$ खींचिए। इन सभी त्रिभुजों के प्रत्येक कोण की माप एक कोण मापक द्वारा माप कर ज्ञात कीजिए। इन मापों को तालिका रूप में इस प्रकार लिखिए,

मापने में हुई संभावित त्रुटियों को ध्यान में रखते हुए आप पाएँगे कि अंतिम स्तंभ में तीनों कोणों का योग $180^{\circ}$ (या लगभग $180^{\circ}$ ) ही है।

पूर्णयता शुद्ध माप संभव होने पर हम यही पाएँगे कि त्रिभुज के तीनों कोणों की मापों का योग $180^{\circ}$ होता है ।

अब आप अपने इस निर्णय को तर्कपूर्ण कथनों द्वारा चरणबद्ध रूप में प्रस्तुत कर सकते हैं।

कथन त्रिभुज के तीनों कोणों की मापों का योग $180^{\circ}$ होता है । इस तथ्य को स्थापित करने के लिए हम त्रिभुज के बाह्य कोण के गुण का उपयोग करते हैं।

दिया है : $\triangle \mathrm{ABC}$ के तीन कोण $\angle 1, \angle 2$ तथा $\angle 3$ हैं (आकृति 6.17)।

$\angle 4$ एक बाहय कोण है जो भुजा $\overline{\mathrm{BC}}$ को $\mathrm{D}$ तक बढ़ाने पर बनता है।

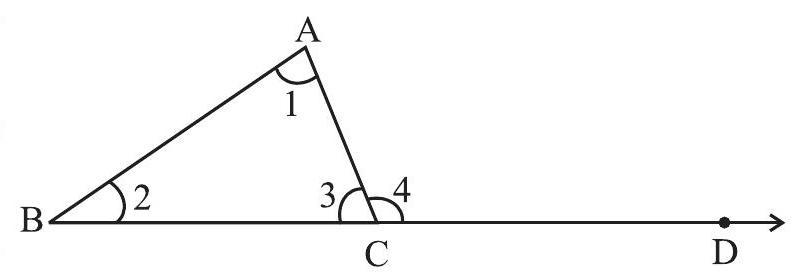
आकृति 6.17

उपपत्ति $\angle 1+\angle 2=\angle 4$ (बाहय कोण का गुण)

$\angle 1+\angle 2+\angle 3=\angle 4+\angle 3$ (दोनों पक्षों में $\angle 3$ योग करने पर)

परंतु $\angle 4$ तथा $\angle 3$ एक रैखिक युग्म बनाते हैं। अतः, इनका योग $180^{\circ}$ है। अर्थात् $\angle 1+\angle 2+\angle 3=180^{\circ}$

आइए, अब देखें कि त्रिभुज के कोणों के इस गुण को, विभिन्न समस्याएँ हल करने में हम कैसे उपयोग कर सकते हैं।

उदाहरण 2 दी गई आकृति 6.18 में $\angle \mathrm{P}$ की माप ज्ञात कीजिए।

हल त्रिभुज के कोणों का योग गुण से $\mathrm{m} \angle \mathrm{P}+47^{\circ}+52^{\circ}=180^{\circ}$

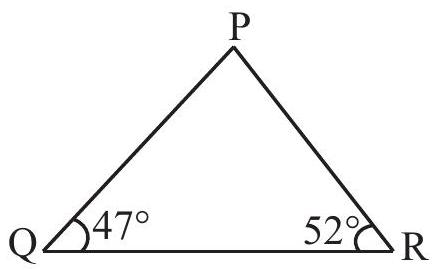
Fig 6.18

अत: $\mathrm{m} \angle \mathrm{P}=180^{\circ}-47^{\circ}-52^{\circ}=180^{\circ}-99^{\circ}=81^{\circ}$

प्रश्नावली 6.3

1. निम्नांकित आकृतियों में अज्ञात $x$ का मान ज्ञात कीजिए।

2. निम्नांकित आकृतियों में अज्ञात $x$ और $y$ का मान ज्ञात कीजिए।

प्रयास कीजिए

1. एक त्रिभुज के दो कोण $30^{\circ}$ तथा $80^{\circ}$ हैं। इस त्रिभुज का तीसरा कोण ज्ञात कीजिए।

2. किसी त्रिभुज का एक कोण $80^{\circ}$ है तथा शेष दोनों कोण बराबर हैं। बराबर कोणों में प्रत्येक की माप ज्ञात कीजिए।

3. किसी त्रिभुज के तीनों कोणों में $1: 2: 1$ का अनुपात है। त्रिभुज के तीनों कोण ज्ञात कीजिए। त्रिभुज का दोनों प्रकार से वर्गीकरण भी कीजिए।

सोचिए, चर्चा कीजिए और लिखिए

1. क्या कोई ऐसा त्रिभुज संभव है जिसके दो कोण समकोण हों ?

2. क्या कोई ऐसा त्रिभुज संभव है जिसमें दो कोण अधिक कोण हों ?

3. क्या कोई ऐसा त्रिभुज संभव है जिसमें दो कोण न्यून कोण हों ?

4. क्या कोई ऐसा त्रिभुज संभव है जिसमें तीनों कोण $60^{\circ}$ से अधिक हों ?

5. क्या कोई ऐसा त्रिभुज संभव है जिसमें तीनों कोण $60^{\circ}$ के हों ?

6. क्या कोई ऐसा त्रिभुज संभव है जिसमें तीनों कोण $60^{\circ}$ से कम के हों ?

6.6 दो विशेष त्रिभुज : समबाहु तथा समद्विबाहु

एक त्रिभुज, जिसकी तीनों भुजाओं की माप समान हो, समबाहु त्रिभुज कहलाता है।

एक समबाहु त्रिभुज $\mathrm{ABC}$ (आकृति 6.19) बनाइए। इसका प्रतिरूप यानी इसी माप का एक और समबाहु त्रिभुज कागज़ से काटें। पहले त्रिभुज को स्थिर रखते हुए इस पर दूसरा त्रिभुज इसे ढकते हुए रखें। दूसरा त्रिभुज पहले को पूरी तरह ढक लेता है । दूसरे त्रिभुज को पहले त्रिभुज पर किसी भी तरह घुमाकर रखें, वे दोनों त्रिभुज फिर भी एक दूसरे को ढक लेते हैं। क्या आप देख पाते हैं कि यदि त्रिभुज की तीनों भुजाएँ समान माप की हैं तब तीनों कोण भी समान माप के ही होते हैं। हम निष्कर्ष निकालते हैं $\mathrm{B}$ कि समबाहु त्रिभुज में (i) तीनों भुजाएँ समान माप की होती हैं। (ii) प्रत्येक कोण की माप $60^{\circ}$ होती है।

आकृति 6.19

एक त्रिभुज, जिसकी दो भुजाओं की माप समान हों, एक समद्विबाहु त्रिभुज कहलाता है।

आकृति 6.20

कागज़ के टुकड़े से एक समद्विबाहु त्रिभुज $\mathrm{XYZ}$, काटिए, जिसमें भुजा $\mathrm{XY}=$ भुजा $\mathrm{XZ}$ हो (आकृति 6.20)। इसे इस प्रकार मोड़िए जिससे शीर्ष $\mathrm{Z}$ शीर्ष $\mathrm{Y}$ पर आच्छादित हो। अब शीर्ष $\mathrm{X}$ से गुज़रने वाली रेखा XM इस त्रिभुज का सममित अक्ष है (जिसके बारे में आप अध्याय 14 में पढ़ेंगे)। आप देखते हैं कि $\angle \mathrm{Y}$ और $\angle \mathrm{Z}$ एक दूसरे को पूर्णतया ढक लेते हैं। $\mathrm{XY}$ और $\mathrm{XZ}$ त्रिभुज की सम भुजाएँ कहलाती हैं। $\mathrm{YZ}$ आधार कहलाता है; $\angle \mathrm{Y}$ तथा $\angle \mathrm{Z}$ आधार कोण कहलाते हैं जो परस्पर समान होते हैं।

इस प्रकार हम निष्कर्ष निकालते हैं कि समद्विबाहु त्रिभुज में (i) दो भुजाएँ बराबर लंबाई की होती हैं। (ii) समान भुजाओं के सामने का कोण समान होता है।

प्रयास कीजिए

1. प्रत्येक आकृति में कोण $x$ का मान ज्ञात कीजिए।

2. प्रत्येक आकृति में कोण $x$ तथा $y$ का मान ज्ञात कीजिए।

6.7 एक त्रिभुज की दो भुजाओं की मापों का योग

1. अपने खेल के मैदान में तीन बिंदु $\mathrm{A}, \mathrm{B}$ तथा $\mathrm{C}$ अंकित कीजिए जो एक ही रेखा में न हों। चूना पाउडर लेकर $\mathrm{AB}, \mathrm{BC}$ तथा $\mathrm{AC}$ पथ निर्धारित कीजिए।

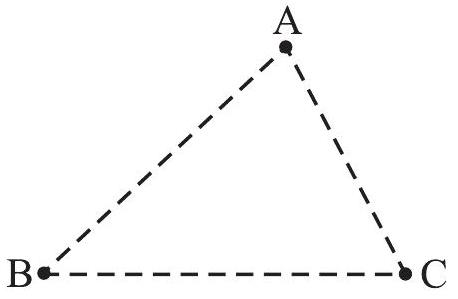
आकृति 6.21

अपने किसी मित्र से कहिए कि वह निर्धारित पथों का उपयोग कर किसी प्रकार $\mathrm{A}$ से प्रारंभ कर $\mathrm{C}$ तक पहुँचे । उदाहरण के लिए, वह पहले पथ $\overline{\mathrm{AB}}$ पर और फिर पथ $\overline{\mathrm{BC}}$ पर चलकर $\mathrm{C}$ पर पहुँचें अथवा पथ $\overline{\mathrm{AC}}$ पर चलकर सीधे $\mathrm{C}$ पर पहुँच जाए। स्वाभाविक है कि वह सीधा पथ $\mathrm{AC}$ पसंद् करेगी। अगर वह कोई अन्य पथ (जैसे $\overline{\mathrm{AB}}$ फिर $\overline{\mathrm{BC}}$ ) लेगी, तब उसे अधिक दूरी चलनी पड़ेगी। दूसरे शब्दों में

$\mathrm{AB}+\mathrm{BC}>\mathrm{AC} \quad \quad \quad \quad \quad \quad \text{(i)}$

इसी प्रकार यदि वह $\mathrm{B}$ से प्रारंभ कर $\mathrm{A}$ पर पहुँचना चाहती है तब वह पहले पथ

$\overline{\mathrm{BC}}$ और फिर पथ $\overline{\mathrm{CA}}$ नहीं लेगी बल्कि वह पथ $\overline{\mathrm{BA}}$ लेकर सीधा $\mathrm{B}$ से $\mathrm{A}$ पर पहुँचेगी। यह इसलिए कि

$\mathrm{BC}+\mathrm{CA}>\mathrm{AB} \quad \quad \quad \quad \quad \quad \text {(ii)}$

इसी प्रकार तर्क करने पर हम देखते हैं कि

$\mathrm{CA}+\mathrm{AB}>\mathrm{BC} \quad \quad \quad \quad \quad \quad \text {(iii)}$

इससे पता चलता है कि किसी त्रिभुज की दो भुजाओं की मापों का योग तीसरी भुजा की माप से बड़ा होता है।

2. अलग-अलग मापों वाली 15 छोटी तीलियाँ (या पट्टियाँ) लीजिए। उनकी मापें, मान लीजिए

$6 \mathrm{~cm}, 7 \mathrm{~cm}, 8 \mathrm{~cm} ,9 \mathrm{~cm}$, $…….$ $20 \mathrm{~cm}$ हैं।

इनमें से कोई तीन तीलियाँ लेकर त्रिभुज बनाने का प्रयत्न कीजिए। तीन-तीन तीलियों के विभिन्न समूह लेकर इस प्रक्रिया को दोहराइए।

मान लीजिए पहले आप दो तीलियाँ $6 \mathrm{~cm}$ व $12 \mathrm{~cm}$ लंबी लेते हैं। तीसरी तीली $12-6=6 \mathrm{~cm}$ से अधिक लंबी लेकिन $12+6=18 \mathrm{~cm}$ से कम लंबी लेनी होगी। यह सब करके देखिए और पता लगाइए कि ऐसा क्यों आवश्यक है ।

एक त्रिभुज बनाने के लिए, आपको तीन तीलियाँ इस प्रकार चुननी होंगी जिससे कि उनमें, कोई दो तीलियों की लंबाइयों का योग तीसरी तीली की लंबाई से अधिक हो।

इस प्रक्रिया से यह भी पता चलता है कि एक त्रिभुज की दो भुजाओं की मापों का योग तीसरी भुजा की माप से अधिक होता है ।

3. अपनी अभ्यास-पुस्तिका में कोई तीन त्रिभुज, जैसे $\triangle \mathrm{ABC}, \triangle \mathrm{PQR}$ तथा $\triangle \mathrm{XYZ}$ बनाइए (आकृति 6.22)।

आकृति 6.22

अपने पैमाने (रूलर) की सहायता से इन त्रिभुजों की भुजाओं को माप कर, एक तालिका के रूप में निम्न प्रकार से लिखिए :

इस प्रक्रिया से हमारे पिछले अनुमान की भी पुष्टि होती है। अतः हम निष्कर्ष निकालते हैं कि एक त्रिभुज की कोई दो भुजाओं की मापों का योग, तीसरी भुजा की माप से अधिक होती है ।

साथ ही हमें यह भी पता चलता है कि एक त्रिभुज की किसी दो भुजाओं का अंतर, तीसरी भुजा की माप से कम होता है।

उदाहरण 3 क्या कोई ऐसा त्रिभुज संभव है जिसकी भुजाओं की मापें $10.2 \mathrm{~cm}, 5.8 \mathrm{~cm}$ तथा $4.5 \mathrm{~cm}$ हों ?

हल मान लीजिए ऐसा त्रिभुज संभव है। तब इस त्रिभुज की कोई भी दो भुजाओं की लंबाइयों का योग तीसरी भुजा की लंबाई से अधिक होगा। आइए, जाँच करके देखें :

अतः, इन भुजाओं वाला त्रिभुज संभव है।

उदाहरण 4 एक त्रिभुज की दो भुजाओं की माप $6 \mathrm{~cm}$ तथा $8 \mathrm{~cm}$ हैं। इसकी तीसरी भुजा की माप किन दो संख्याओं के बीच होगी ?

हल हम जानते हैं कि त्रिभुज की कोई दो भुजाओं का योग तीसरी से अधिक होता है।

अतः, तीसरी भुजा, दी हुई दो भुजाओं के योग से कम होनी चाहिए। अर्थात् तीसरी भुजा $8+6=14 \mathrm{~cm}$ से कम होगी ।

यह तीसरी भुजा दी हुई दोनों भुजाओं के अंतर से अधिक होनी चाहिए। अर्थात् तीसरी भुजा $8-6=2 \mathrm{~cm}$ से अधिक होगी ।

तीसरी भुजा की माप $2 \mathrm{~cm}$ से अधिक तथा $14 \mathrm{~cm}$ से कम होनी चाहिए।

प्रश्नावली 6.4

1. निम्न दी गई भुजाओं की मापों से क्या कोई त्रिभुज संभव है ?

(i) $2 \mathrm{~cm}, 3 \mathrm{~cm}, 5 \mathrm{~cm}$

(ii) $3 \mathrm{~cm}, 6 \mathrm{~cm}, 7 \mathrm{~cm}$

(iii) $6 \mathrm{~cm}, 3 \mathrm{~cm}, 2 \mathrm{~cm}$

2. त्रिभुज $\mathrm{PQR}$ के अभ्यंतर में कोई बिंदु $\mathrm{O}$ लीजिए। क्या यह सही है कि

(i) $\mathrm{OP}+\mathrm{OQ}>\mathrm{PQ}$ ?

(ii) $\mathrm{OQ}+\mathrm{OR}>\mathrm{QR}$ ?

(iii) $\mathrm{OR}+\mathrm{OP}>\mathrm{RP}$ ?

3. त्रिभुज $\mathrm{ABC}$ की एक माध्यिका $\mathrm{AM}$ है। बताइए कि क्या $\mathrm{AB}+\mathrm{BC}+\mathrm{CA}>2 \mathrm{AM}$ ?

(संकेत : $\triangle \mathrm{ABM}$ तथा $\triangle \mathrm{AMC}$ की भुजाओं पर विचारकीजिए।)

4. $\mathrm{ABCD}$ एक चतुर्भुज है । क्या $\mathrm{AB}+\mathrm{BC}+\mathrm{CD}+\mathrm{DA}>\mathrm{AC}+\mathrm{BD}$ ?

5. $\mathrm{ABCD}$ एक चतुर्भुज है। क्या $\mathrm{AB}+\mathrm{BC}+\mathrm{CD}+\mathrm{DA}<2(\mathrm{AC}+\mathrm{BD})$ ?

6. एक त्रिभुज की दो भुजाओं की माप $12 \mathrm{~cm}$ तथा $15 \mathrm{~cm}$ है। इसकी तीसरी भुजा की माप किन दो मापों के बीच होनी चाहिए ?

सोचिए, चर्चा कीजिए और लिखिए

1. किसी त्रिभुज में क्या उसके कोई दो कोणों का योग तीसरे कोण से सदैव अधिक होता है ?

6.8 समकोण त्रिभुज तथा पाइथागोरस गुण

ईसा से छठी शताब्दी पूर्व, एक यूनानी दार्शनिक पाइथागोरस ने, समकोण त्रिभुज से संबंधित एक बहुत उपयोगी व महत्वपूर्ण गुण के बारे में पता लगाया, जिसे हम इस अनुभाग में बता रहे हैं। अतः इस गुण को उनके नाम से ही जाना जाता है। वास्तव में इस गुण का ज्ञान कुछ अन्य देशों के लोगों को भी था। भारतीय गणितज्ञ बौधायन ने भी इस गुण के समकक्ष एक गुण की जानकारी दी थी।

आकृति 6.23

अब हम पाइथागोरस गुण का विस्तार से अध्ययन करते हैं।

समकोण त्रिभुज में उसकी भुजाओं को विशेष नाम दिए जाते हैं। समकोण के सामने वाली भुजा को कर्ण कहते हैं। अन्य दो भुजाओं को समकोण त्रिभुज के पाद (legs) कहते हैं।

$\triangle \mathrm{ABC}$ में (आकृति 6.23), शीर्ष $\mathrm{B}$ पर समकोण बना है। अतः, $\mathrm{AC}$ इसका कर्ण है। $\overline{\mathrm{AB}}$ तथा $\overline{\mathrm{BC}}$ समकोण त्रिभुज $\mathrm{ABC}$ के दो पाद हैं।

किसी भी माप का एक समकोण त्रिभुज लेकर उसके आठ प्रतिरूप बनाइए। उदाहरण के लिए एक समकोण त्रिभुज लेते हैं जिसके कर्ण की माप $a$ इकाई तथा उसके दो पादों की माप $b$ इकाई तथा $c$ इकाई है (आकृति 6.24)।

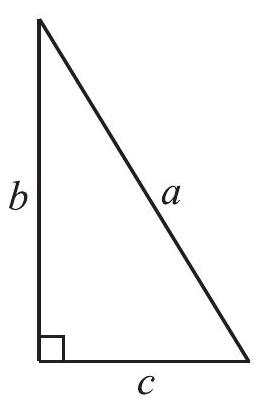
आकृति 6.24

एक कागज़ पर एक समान माप वाले दो वर्ग बनाइए जिनकी भुजाओं की माप $b+c$ के बराबर हो ।

अब अपने आठ त्रिभुजों में से चार त्रिभुजों को वर्ग $\mathrm{A}$ में तथा चार त्रिभुजों को वर्ग $\mathrm{B}$ में स्थापित कीजिए जैसा कि निम्न आकृति में दिखाया गया है (आकृति 6.25)।

आप जानते हैं कि दोनों वर्ग एकरूप हैं यानी एक समान हैं तथा रखे गए आठों त्रिभुज भी एक समान हैं।

अतः वर्ग $\mathrm{A}$ का अनाच्छदित क्षेत्रफल $=$ वर्ग $\mathrm{B}$ का अनाच्छादित क्षेत्रफल

अथवा वर्ग $\mathrm{A}$ के भीतर वाले वर्ग का क्षेत्रफल $=$ वर्ग $\mathrm{B}$ के भीतर दोनों अनाच्छादित वर्गों के क्षेत्रफल का योग अर्थात्

$ a^{2}=b^{2}+c^{2} $

यह पाइथागोरस गुण है। इसे इस प्रकार कहा जा सकता है :

आकृति 6.26 समझ लें।

एक समकोण त्रिभुज में

कर्ण पर बना वर्ग $=$ पादों पर बने दोनों वर्गों का योग

पाइथागोरस गुण, गणित में एक बहुत ही महत्वपूर्ण गुण है। आगे की कक्षाओं में इसे एक साध्य के रूप में विधिपूर्वक सिद्ध भी किया जाएगा। अभी आप इसके तात्पर्य को भली भांति

आकृति 6.26

इसके अनुसार, किसी समकोण त्रिभुज में कर्ण पर बने वर्ग का क्षेत्रफल दोनों पादों पर बने वर्गों के क्षेत्रफल के योग के बराबर होता है ।

एक वर्गाकार कागज़ लेकर, उस पर एक समकोण त्रिभुज बनाइए। इसकी भुजाओं पर वर्गों के क्षेत्रफल ज्ञात कीजिए और इस साध्य की व्यावहारिक रूप से जाँच कीजिए (आकृति 6.26)।

यदि कोई त्रिभुज, समकोण त्रिभुज है तब उस पर पाइथागोरस गुण प्रयुक्त होता है। अब यदि किसी त्रिभुज पर पाइथागोरस गुण सत्य है तो क्या यह एक समकोण त्रिभुज होगा ? (ऐसी समस्याओं को हम विलोम समस्याएँ कहते हैं।) हम इस बात का उत्तर देने का प्रयत्न करेंगे। अब हम दिखाएँगे कि यदि किसी त्रिभुज में कोई दो भुजाओं के वर्गों का योग, तीसरी भुजा के वर्ग के बराबर है तब वह एक समकोण त्रिभुज होना चाहिए।

इनें कीजिए

1. $4 \mathrm{~cm}, 5 \mathrm{~cm}$ तथा 6 सेमी लंबी भुजाओं वाले तीन वर्ग कागज़ से काटिए। इन तीनों वर्गों के तीन शीर्षों को मिलाते हुए इस प्रकार व्यवस्थित कर रखिए कि उनकी भुजाओं से एक त्रिभुज प्राप्त हो (आकृति 6.27)। इस प्रकार प्राप्त त्रिभुज को कागज़ पर चिन्हित कीजिए। इस त्रिभुज के तीनों कोणों को मापिए। आप देखेंगे कि इनमें कोई भी समकोण नहीं है। ध्यान दीजिए कि

$ 4^{2}+5^{2} \neq 6^{2}, 5^{2}+6^{2} \neq 4^{2} \text { तथा } 6^{2}+4^{2} \neq 5^{2} $

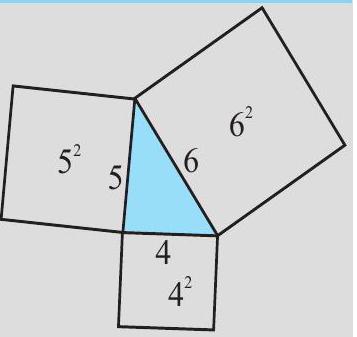
आकृति 6.27

2. उपर्युक्त प्रक्रिया को $4 \mathrm{~cm}, 5 \mathrm{~cm}$ तथा $7 \mathrm{~cm}$ भुजाओं वाले तीन वर्ग लेकर फिर दोहराइए। इस बार आपको एक अधिक कोण त्रिभुज प्राप्त होगा। यहाँ ध्यान दीजिए कि $ 4^{2}+5^{2} \neq 7^{2} $ इत्यादि ।

इस प्रक्रिया से पता चलता है कि पाइथागोरस गुण केवल तभी प्रयुक्त होता है जब कि त्रिभुज एक समकोण त्रिभुज होगा।

अतः हमें यह तथ्य प्राप्त होता है :

यदि किसी त्रिभुज पर पाइथागोरस गुण प्रयुक्त होता है, तभी वह एक समकोण त्रिभुज होगा।

उदाहरण 5 एक त्रिभुज की भुजाएँ $3 \mathrm{~cm}, 4 \mathrm{~cm}$ तथा $5 \mathrm{~cm}$ लंबी हैं। निर्धारित कीजिए कि क्या वह एक समकोण त्रिभुज है ?

हल $3^{2}=3 \times 3=9 ; 4^{2}=4 \times 4=16 ; 5^{2}=5 \times 5=25$

हम देखते हैं कि $3^{2}+4^{2}=5^{2}$

अतः, यह त्रिभुज, एक समकोण त्रिभुज है।

ध्यान दीजिए : किसी भी समकोण त्रिभुज में कर्ण सबसे लंबी भुजा होती है। इस उदाहरण में $5 \mathrm{~cm}$ लंबी भुजा ही कर्ण है ।

उदाहरण 6 $ \Delta \mathrm{ABC}$ का $\mathrm{C}$ एक समकोण है । यदि $\mathrm{AC}=5 \mathrm{~cm}$ तथा $\mathrm{BC}=12 \mathrm{~cm}$, तब $\mathrm{AB}$ की लंबाई ज्ञात कीजिए।

हल सहायता के लिए अनुमान से एक उपयुक्त आकृति बनाते हैं (आकृति 6.28)।

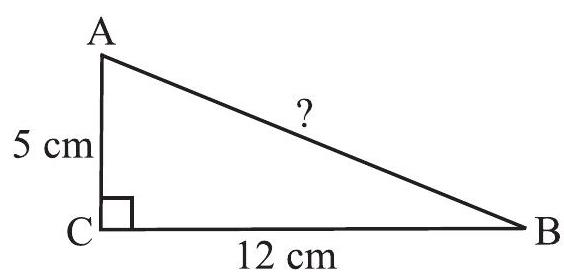
आकृति 6.28

पाइथागोरस गुण से,

$\mathrm{AB}^{2} =\mathrm{AC}^{2}+\mathrm{BC}^{2} $

$ =5^{2}+12^{2}=25+144=169=13^{2}$

अर्थात्: $\mathrm{AB}^{2}=13^{2}$. अतः, $\mathrm{AB}=13$ है। अर्थात् $\mathrm{AB}$ की लंबाई $13 \mathrm{~cm}$ है ।

ध्यान रखें: पूर्ण वर्ग संख्याएँ पहचानने के लिए आप अभाज्य गुणनखंड विधि प्रयोग में ला सकते हैं।

प्रयास कीजिए

निम्न आकृति 6.29 में अज्ञात लंबाई $x$ ज्ञात कीजिए:

आकृति 6.29

प्रश्नावली 6.5

1. $\mathrm{PQR}$ एक त्रिभुज है जिसका $\mathrm{P}$ एक समकोण है। यदि $\mathrm{PQ}=10 \mathrm{~cm}$ तथा $\mathrm{PR}=24 \mathrm{~cm}$ तब $\mathrm{QR}$ ज्ञात कीजिए।

2. $\mathrm{ABC}$ एक त्रिभुज है जिसका $\mathrm{C}$ एक समकोण है । यदि $\mathrm{AB}=25 \mathrm{~cm}$ तथा $\mathrm{AC}=7 \mathrm{~cm}$ तब $\mathrm{BC}$ ज्ञात कीजिए।

3. दीवार के सहारे उसके पैर कुछ दूरी पर टिका कर $15 \mathrm{~m}$ लंबी एक सीढ़ी भूमि से $12 \mathrm{~m}$ ऊँचाई पर स्थित खिड़की तक पहुँच जाती है। दीवार से सीढ़ी के पैर की दूरी ज्ञात कीजिए।

4. निम्नलिखित में भुजाओं के कौन से समूह एक समकोण त्रिभुज बना सकते हैं ?

(i) $2.5 \mathrm{~cm}, 6.5 \mathrm{~cm}, 6 \mathrm{~cm}$

(ii) $2 \mathrm{~cm}, 2 \mathrm{~cm}, 5 \mathrm{~cm}$

(iii) $1.5 \mathrm{~cm}, 2 \mathrm{~cm}, 2.5 \mathrm{~cm}$

समकोण त्रिभुज होने की स्थिति में उसके समकोण को भी पहचानिए।

5. एक पेड़ भूमि से $5 \mathrm{~m}$ की ऊँचाई पर टूट जाता है और उसका ऊपरी सिरा भूमि को उसके आधार से $12 \mathrm{~m}$ की दूरी पर छूता है। पेड़ की पूरी ऊँचाई ज्ञात कीजिए।

6. त्रिभुज $\mathrm{PQR}$ में कोण $\mathrm{Q}=25^{\circ}$ तथा कोण $\mathrm{R}=65^{\circ}$. हैं। निम्नलिखित में कौन सा कथन सत्य है ?

(i) $\mathrm{PQ}^{2}+\mathrm{QR}^{2}=\mathrm{RP}^{2}$

(ii) $\mathrm{PQ}^{2}+\mathrm{RP}^{2}=\mathrm{QR}^{2}$

(iii) $\mathrm{RP}^{2}+\mathrm{QR}^{2}=\mathrm{PQ}^{2}$

7. एक आयत की लंबाई $40 \mathrm{~cm}$ है तथा उसका एक विकर्ण $41 \mathrm{~cm}$ है। इसका परिमाप ज्ञात कीजिए।

8. एक समचतुर्भुज के विकर्ण $16 \mathrm{~cm}$ तथा $30 \mathrm{~cm}$ हैं। इसका परिमाप ज्ञात कीजिए।

सोचिए, चर्चा कीजिए और लिखिए

1. त्रिभुज $\mathrm{PQR}$ का कोण $\mathrm{P}$ एक समकोण है। इसकी सबसे लंबी भुजा कौन-सी है ?

2. त्रिभुज $\mathrm{ABC}$ का कोण $\mathrm{B}$ एक समकोण है। इसकी सबसे लंबी भुजा कौन-सी है ?

3. किसी समकोण त्रिभुज में सबसे लंबी भुजा कौन-सी होती है ?

4. किसी आयत में विकर्ण पर बने वर्ग का क्षेत्रफल उसकी लंबाई तथा चौड़ाई पर बने वर्गों के क्षेत्रफल के योग के बराबर होता है। यह बौधायन का प्रमेय है। इसकी पाइथागोरस गुण से तुलना कीजिए।

इन्हें कीजिए

ज्ञानवर्द्धक क्रियाकलाप

आकृतियों को जोड़ अथवा तोड़कर, पाइथागोरस साध्य को अनेक विधियों से सिद्ध किया गया है। इन विधियों में से कुछ को एकत्रित कर उन्हें एक चार्ट बनाकर प्रस्तुत कीजिए।

हमने क्या चर्चा की?

1. एक त्रिभुज की तीन भुजाएँ तथा तीन कोण, इसके छः अवयय कहलाते हैं।

2. किसी त्रिभुज के एक शीर्ष को उसके सम्मुख भुजा के मध्य बिंदु से मिलाने वाले रेखाखंड को उसकी एक माध्यिका कहते हैं। एक त्रिभुज की तीन माध्यिकाएँ होती हैं।

3. किसी त्रिभुज के एक शीर्ष से उसके सम्मुख भुजा पर खींचे गए लंब को त्रिभुज का एक शीर्षलंब कहते हैं। एक त्रिभुज के तीन शीर्षलंब होते हैं।

4. किसी त्रिभुज का बाह्य कोण किसी एक भुजा को एक ही ओर बढ़ाने पर बनता है। प्रत्येक शीर्ष पर, एक भुजा को दो प्रकार से बढ़ाकर दो बाह्य कोण बनाए जा सकते हैं।

5. बाह्य कोण का एक गुण -

त्रिभुज के बाह्य कोण की माप, उसके दो सम्मुख अंतःकोणों के योग के बराबर होती है।

6. त्रिभुज के कोणों के योग का गुण -

एक त्रिभुज के तीनों कोणों का योग $180^{\circ}$ होता है ।

7. एक त्रिभुज जिसकी प्रत्येक भुजा की माप समान हो, समबाहु त्रिभुज कहलाता है। समबाहु त्रिभुज का प्रत्येक कोण $60^{\circ}$ का होता है।

8. एक त्रिभुज, जिसकी कोई दो भुजाएँ माप में समान हों, समद्विबाहु त्रिभुज कहलाता है। समद्विबाहु त्रिभुज की असमान भुजा उसका आधार कहलाती है तथा आधार पर बने दोनों कोण एक दूसरे के बराबर होते हैं।

9. त्रिभुज की भुजाओं से संबंधित गुण-

(i) त्रिभुज की कोई दो भुजाओं की मापों का योग, तीसरी भुजा की माप से अधिक होता है ।

(ii) त्रिभुज की कोई दो भुजाओं की मापों का अंतर, तीसरी भुजा की माप से कम होता है । यें दोनों गुण, किसी त्रिभुज की रचना की संभावना बताने में उपयोगी होते हैं जब कि उसकी तीनों भुजाओं की माप दी हों ।

10. समकोण त्रिभुज में समकोण के सामने वाली भुजा कर्ण तथा अन्य दोनों भुजाएँ उसके पाद कहलाती हैं।

11. पाइथागोरस गुण-

एक समकोण त्रिभुज में कर्ण का वर्ग = उसके पादों के वर्गों का योग।

यदि एक त्रिभुज, समकोण त्रिभुज नहीं है तब यह गुण प्रयुक्त नहीं होता है । यह गुण इस बात को तय करने में उपयोगी होता है कि कोई दिया गया त्रिभुज समकोण त्रिभुज है या नहीं।