5.1 रेखा

आप पहले से ही जानते हैं कि किसी दिए हुए आकार में विभिन्न रेखाएँ, रेखाखंडों एवं कोणों की पहचान कैसे की जाती है। क्या आप निम्नलिखित आकृतियों में विभिन्न रेखाखंडों एवं कोणों की पहचान कर सकते हैं? (आकृति 5.1)

आकृति 5.1

क्या आप यह भी जान सकते हैं कि निर्मित कोण, न्यून कोण अथवा अधिक कोण अथवा सम कोण हैं? स्मरण कीजिए कि एक रेखाखंड के दो अंत बिंदु होते हैं। यदि हम इन दो अंत बिंदुओं को अपनी-अपनी दिशाओं में अपरिमित रूप में बढ़ाते हैं तो हमें एक रेखा प्राप्त होती है। इस प्रकार हम कह सकते हैं कि एक रेखा का कोई अंत बिंदु नहीं होता है। दूसरी तरफ़ स्मरण कीजिए कि किरण का एक अंत बिंदु (नामतः प्रारंभिक बिंदु) होता है। उदाहरणतः नीचे दी हुई आकृतियों को देखिए:

आकृति 5.2

यहाँ आकृति 5.2 (i) रेखाखंड, आकृति 5.2 (ii) रेखा एवं आकृति 5.2 (iii) एक किरण, को दर्शाती है। सामान्यतः एक रेखाखंड $\mathrm{PQ}$ को संकेत $\overline{\mathrm{PQ}}$, रेखा $\mathrm{AB}$ को संकेत $\mathrm{AB}$ एवं किरण $\mathrm{OP}$ को संकेत $\overrightarrow{\mathrm{OP}}$, से निर्दिष्ट किया जाता है। अपने दैनिक जीवन से रेखाखंडों एवं किरणों के कुछ उदाहरण दीजिए और उनके बारे में अपने मित्रों से चर्चा कीजिए।

पुनः स्मरण कीजिए कि रेखाएँ अथवा रेखाखंडों के मिलने पर कोण निर्मित होता है। उपर्युक्त आकृतियों (आकृति 5.1) में कोनों (corners) को प्रेक्षित कीजिए। जब दो रेखाएँ अथवा रेखाखंड किसी बिंदु पर प्रतिच्छेद करते हैं तो इन कोनों का निर्माण होता है। उदाहरणतः नीचे दी हुई आकृतियों को देखिए:

आकृति 5.3

आकृति 5.3 (i) में रेखाखंड $A B$ एवं $B C$, कोण $A B C$ का निर्माण करने के लिए, एक दूसरे को बिंदु $\mathrm{B}$ पर प्रतिच्छेद करते हैं और रेखाखंड $\mathrm{BC}$ एवं $\mathrm{AC}$, कोण $\mathrm{ACB}$ का निर्माण करने के लिए एक दूसरे को $\mathrm{C}$ पर प्रतिच्छेद करते हैं इत्यादि। जबकि आकृति 5.3 (ii) में रेखाएँ $\mathrm{PQ}$ एवं $\mathrm{RS}$ एक दूसरे को बिंदु $\mathrm{O}$ पर प्रतिच्छेद करती हैं जिससे कोण POS, SOQ, $\mathrm{QOR}$ और ROP निर्मित होते हैं। कोण $\mathrm{ABC}$ को संकेत $\angle \mathrm{ABC}$ द्वारा निरूपित किया जाता है। इस प्रकार आकृति 5.3 (i) में निर्मित तीन कोण $\angle \mathrm{ABC}$, $\angle \mathrm{BCA}$ एवं $\angle \mathrm{BAC}$ हैं और आकृति 5.3 (ii) में निर्मित चार कोण $\angle \mathrm{POS}$, $\angle \mathrm{SOQ}, \angle \mathrm{QOR}$ एवं $\angle \mathrm{POR}$ हैं। आप पहले से ही अध्ययन कर चुके हैं कि न्यून कोण, अधिक कोण अथवा सम कोण के रूप में कोणों का वर्गीकरण कैसे किया जाता है।

प्रयास कीजिए

अपने आसपास दस आकृतियों को सूचीबद्ध कीजिए और उनमें पाए जाने वाले न्यून कोणों, अधिक कोणों एवं समकोणों की पहचान कीजिए।

टिप्पणी कोण $\mathrm{ABC}$ के माप के संदर्भ में, $\mathrm{m} \angle \mathrm{ABC}$ को साधारणतः $\angle \mathrm{ABC}$ के रूप में लिखेंगे। प्रकरण से यह बात स्पष्ट हो जाएगी कि हम कोण के संदर्भ में अथवा इसके माप के सदर्भ में बात कर रहे हैं।

5.2 संबंधित कोण

5.2.1 पूरक कोण

जब दो कोणों के मापों का योग $90^{\circ}$ होता है, तो ये कोण पूरक कोण (complementary angles) कहलाते हैं।

$\text { क्या ये दो कोण पूरक कोण हैं? हाँ }$ आकृति 5.4 $\text { क्या ये दो कोण पूरक कोण हैं? नहीं }$

जब दो कोण पूरक होते हैं, तो इनमें से प्रत्येक कोण दूसरे कोण का पूरक कहलाता है। उपर्युक्त आरेख (आकृति 5.4) में " $30^{\circ}$ का कोण", " $60^{\circ}$ के कोण" का पूरक है और विलोमतः

सोचिए, चर्चा कीजिए एवं लिखिए

1. क्या दो न्यून कोण एक दूसरे के पूरक हो सकते हैं?

2. क्या दो अधिक कोण एक दूसरे के पूरक हो सकते हैं?

3. क्या दो समकोण एक दूसरे के पूरक हो सकते हैं?

प्रयास कीजिए

1. निम्नलिखित कोणों के युग्मों में कौन-से पूरक हैं? (आकृति 5.5)

2. निम्नलिखित कोणों में प्रत्येक के पूरक का माप क्या है?

(i) $45^{\circ}$

(ii) $65^{\circ}$

(iii) $41^{\circ}$

(iv) $54^{\circ}$

3. दो पूरक कोणों के मापों का अंतर $12^{\circ}$ है। कोणों के माप ज्ञात कीजिए।

5.2.2 संपूरक कोण

आइए कोणों के निम्नलिखित युग्मों को देखते हैं (आकृति 5.6):

आकृति 5.6

क्या आप देखते हैं कि उपर्युक्त प्रत्येक युग्म में (आकृति 5.6) कोणों के मापों का योग $180^{\circ}$ पाया जाता है ? कोणों के ऐसे युग्म संपूरक कोण (supplementary angles) कहलाते हैं। जब दो कोण संपूरक होते हैं तो उनमें से प्रत्येक कोण दूसरे कोण का संपूरक कहलाता है।

सोचिए, चर्चा कीजिए एवं लिखिए

1. क्या दो अधिक कोण संपूरक हो सकते हैं?

2. क्या दो न्यून कोण संपूरक हो सकते हैं?

3. क्या दो सम कोण संपूरक हो सकते हैं?

प्रयास कीजिए

1. आकृति 5.7 में संपूरक कोणों के युग्म ज्ञात कीजिए :

आकृति 5.7

2. निम्नलिखित कोणों में प्रत्येक के संपूरक का माप क्या होगा?

(i) $100^{\circ}$

(ii) $90^{\circ}$

(iii) $55^{\circ}$

(iv) $125^{\circ}$

3. दो संपूरक कोणों में बड़े कोण का माप छोटे कोण के माप से $44^{\circ}$ अधिक है। कोणों के माप ज्ञात कीजिए।

प्रश्नावली 5.1

1. निम्नलिखित कोणों में से प्रत्येक का पूरक ज्ञात कीजिए :

2. निम्नलिखित कोणों में से प्रत्येक का संपूरक ज्ञात कीजिए।

3. कोणों के निम्नलिखित युग्मों में से पूरक एवं संपूरक युग्मों की पृथक्-पृथक् पहचान कीजिए :

(i) $65^{\circ}, 115^{\circ}$

(ii) $63^{\circ}, 27^{\circ}$

(iii) $112^{\circ}, 68^{\circ}$

(iv) $130^{\circ}, 50^{\circ}$

(v) $45^{\circ}, 45^{\circ}$

(vi) $80^{\circ}, 10^{\circ}$

4. ऐसा कोण ज्ञात कीजिए जो अपने पूरक के समान हो।

5. ऐसा कोण ज्ञात कीजिए जो अपने संपूरक के समान हो।

6. दी हुई आकृति में $\angle 1$ एवं $\angle 2$ संपूरक कोण हैं। यदि $\angle 1$ में कमी की जाती है, तो $\angle 2$ में क्या परिवर्तन होगा ताकि 1 2 दोनों कोण फिर भी संपूरक ही रहें।

7. क्या दो ऐसे कोण संपूरक हो सकते हैं यदि उनमें से दोनों

(i) न्यून कोण हैं?

(ii) अधिक कोण हैं?

(iii) समकोण हैं?

8. एक कोण $45^{\circ}$ से बड़ा है। क्या इसका पूरक कोण $45^{\circ}$ से बड़ा है अथवा $45^{\circ}$ के बराबर है अथवा $45^{\circ}$ से छोटा है?

9. रिक्त स्थानों की पूर्ति कीजिए :

(i) यदि दो कोण पूरक हैं, तो उनके मापों का योग ______________ है।

(ii) यदि दो कोण संपूरक हैं तो उनके मापों का योग ______________ है।

(iii) यदि दो आसन्न कोण संपूरक हैं, तो वे ______________ बनाते हैं।

10. संलग्न आकृति में निम्नलिखित कोण युग्मों को नाम दीजिए :

(i) शीर्षाभिमुख अधिक कोण

(ii) आसन्न पूरक कोण

(iii) समान संपूरक कोण

(iv) असमान संपूरक कोण

(v) आसन्न कोण जो रैखिक युग्म नहीं बनाते हैं।

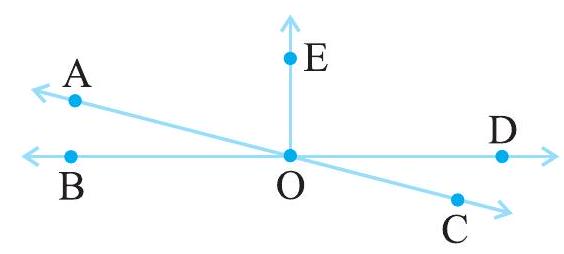
5.3 रेखा-युग्म

5.3.1 प्रतिच्छेदी रेखाएँ

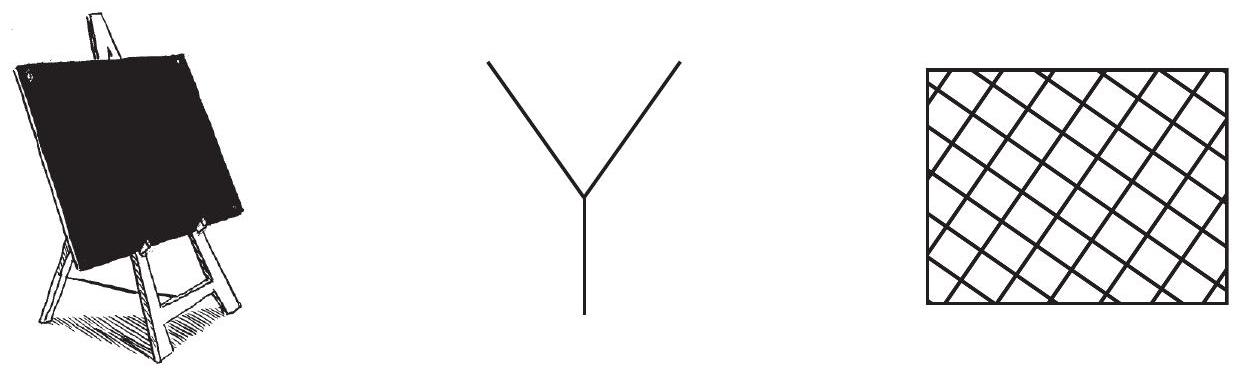
आकृति 5.8

स्टैंड पर रखा हुआ श्यामपट्ट, रेखाखंडों द्वारा निर्मित अक्षर $\mathrm{Y}$ और एक खिड़की का जालीदार दरवाज़ा, इन सभी में उभयनिष्ठ क्या हैं? ये प्रतिच्छेदी रेखाओं (intersecting lines) के उदाहरण हैं (आकृति 5.8)। दो रेखाएँ $l$ और $m$ प्रतिच्छेद् करती हैं यदि उनमें एक बिंदु उभयनिष्ठ है। यह उभयनिष्ठ बिंदु उनका प्रतिच्छेद बिंदु कहलाता है।

आकृति 5.9

आकृति 5.20 में, $\mathrm{AC}$ और $\mathrm{BE}, \mathrm{P}$ पर प्रतिच्छेद करती हैं।

$\mathrm{AC}$ और $\mathrm{BC}, \mathrm{C}$ पर प्रतिच्छेद करती हैं। $\mathrm{AC}$ और $\mathrm{EC}, \mathrm{C}$ पर प्रतिच्छेद करती हैं। प्रतिच्छेदी रेखाखंडों के दस अन्य युग्म ज्ञात करने का प्रयास कीजिए।

क्या दो रेखाएँ अथवा रेखाखंड आवश्यक रूप से प्रतिच्छेद करने चाहिए?

क्या आप इस आकृति में दो रेखाखंडों के युग्म ज्ञात कर सकते हैं जो प्रतिच्छेदी नहीं है? क्या दो रेखाएँ एक से ज्यादा बिंदुओं पर प्रतिच्छेद कर सकती हैं। इसके बारे में विचार कीजिए।

प्रयास कीजिए

1. अपने आसपास के परिवेश से ऐसे उदाहरण ज्ञात कीजिए जहाँ रेखाएँ सम कोण पर प्रतिच्छेद करती हैं।

2. एक समबाहु त्रिभुज के शीर्षों पर प्रतिच्छेदी रेखाओं द्वारा निर्मित कोणों के माप ज्ञात कीजिए।

3. एक आयत खींचिए और प्रतिच्छेदी रेखाओं द्वारा निर्मित चार शीर्षों के कोणों के माप ज्ञात कीजिए।

4. यदि दो रेखाएँ एक-दूसरे को प्रतिच्छेद करती हैं, तो क्या वे हमेशा एक-दूसरे को सम कोण पर प्रतिच्छेद करती हैं?

5.3.2 तिर्यक छेदी रेखा

शायद, आपने दो अथवा अधिक सड़कों को पार करते हुए एक सड़क देखी होगी अथवा कई अन्य रेल पटरियों को पार करते हुए एक रेल पटरी देखी होगी। इनसे तिर्यक छेदी रेखा या तिर्यक रेखा (transversal) का अनुभव प्राप्त होता है (आकृति 5.10)।

आकृति 5.10

एक ऐसी रेखा जो दो अथवा अधिक रेखाओं को भिन्न बिंदुओं पर प्रतिच्छेद करती है, तिर्यक छेदी रेखा (transversal) कहलाती है। आकृति 5.11 में, $p$, रेखाएँ $l$ और $m$ की तिर्यक छेदी रेखा है।

आकृति 5.12 में, $p$ एक तिर्यक छेदी रेखा नहीं है तथापि यह रेखाएँ $l$ और $m$ को काटती है। क्या आप बता सकते हैं ‘क्यों’?

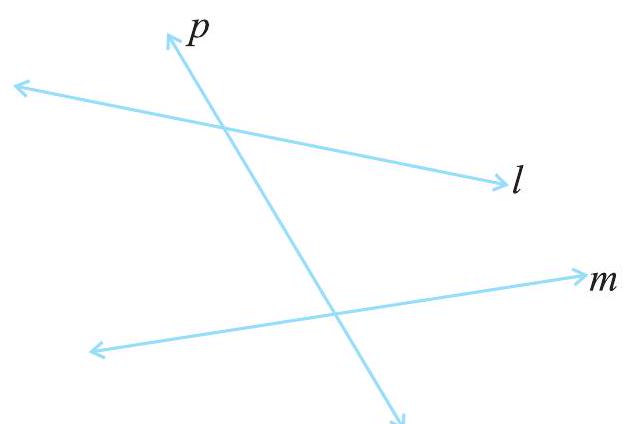
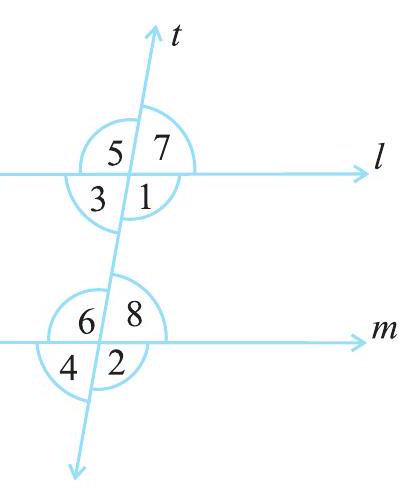
आकृति 5.11

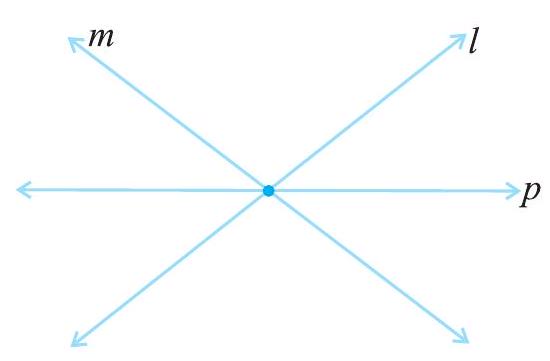
आकृति 5.12

प्रयास कीजिए

1. मान लीजिए दो रेखाएँ दी हुई हैं। इन रेखाओं के लिए आप कितनी तिर्यक छेदी रेखाएँ खींच सकते हैं?

2. यदि एक रेखा तीन रेखाओं की तिर्यक छेदी रेखा है, तो बताइए कितने प्रतिच्छेदन बिंदु हैं।

3. अपने आसपास कुछ तिर्यक छेदी रेखाएँ ढूँढने का प्रयास कीजिए।

5.3.3 तिर्यक छेदी रेखा द्वारा निर्मित कोण

आकृति 5.13 में, आप देखते हैं कि रेखाएँ $l$ एवं $m$ तिर्यक छेदी रेखा $p$ द्वारा काटी जा रही है। इस प्रकार बनने वाले 1 से 8 तक अंकित कोणों के विशिष्ट नाम हैं:

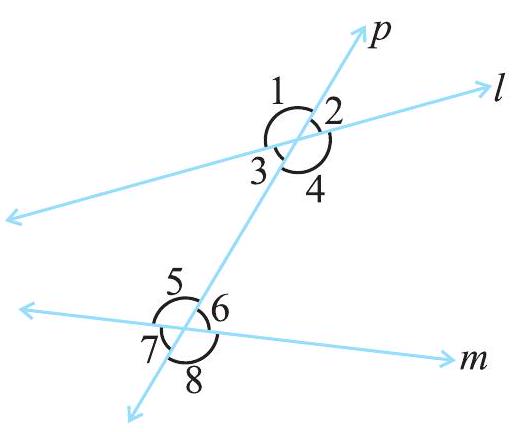
आकृति 5.13

टिप्पणी: आकृति 5.14 में ( $\angle 1$ एवं $\angle 5$ जैसे) संगत कोणों में निम्नलिखित सम्मिलित होते हैं :

(i) विभिन्न शीर्ष

(ii) तिर्यक छेदी रेखा के एक ही तरफ बने होते हैं।

(iii) दो रेखाओं के सापेक्ष संगत स्थितियों (ऊपर अथवा नीचे, बायाँ अथवा दायाँ) में होते हैं।

आकृति 5.14

आकृति 5.15 में ( $\angle 3$ एवं $\angle 6$ जैसे) अंतः एकांतर कोण

(i) के विभिन्न शीर्ष होते हैं।

(ii) तिर्यक छेदी रेखा के सम्मुख स्थिति पर बने होते हैं।

(iii) दो रेखाओं के “मध्य” स्थित होते हैं।

आकृति 5.15

प्रयास कीजिए

प्रत्येक आकृति में कोण-युग्म को नाम दीजिए :

5.3.4 समांतर रेखाओं की तिर्यक छेदी रेखा

क्या आपको याद है कि समांतर रेखाएँ क्या हैं । ये किसी तल में ऐसी रेखाएँ होती हैं जो एक-दूसरे से कहीं नहीं मिलती। क्या आप निम्नलिखित आकृतियों में समांतर रेखाओं की पहचान कर सकते हैं? (आकृति 5.16)

आकृति 5.16

समांतर रेखाओं की तिर्यक छेदी रेखा या तिर्यक रेखा से बहुत ही रुचिकर परिणाम प्राप्त होते हैं।

इन्हें कीजिए

एक रेखांकित कागज़ लीजिए। दो मोटी रंगीली समांतर रेखाएँ $l$ और $m$ खींचिए। रेखाएँ $l$ और $m$ की एक तिर्यक छेदी रेखा $t$ खींचिए। $\angle 1$ और $\angle 2$ को लेबल कीजिए जैसा कि आकृति 5.17(i) में दर्शाया गया है।

खींची गई आकृति पर एक अनुरेखण कागज़ (ट्रेसिंग पेपर) रखिए। रेखाएँ $l, m$ और $t$ की प्रतिलिपि बनाइए।

ट्रेसिंग पेपर को $t$ के अनु तब तक खिसकाइए जब तक $l, m$ के संपाती न हो जाए।

आप पाते हैं कि प्रतिलिपित आकृति का $\angle 1$, मूल आकृति के $\angle 2$ के संपाती हो जाता है।

वास्तव में आप निम्नलिखित परिणामों को अनुरेखण एवं खिसकाने के क्रियाकलाप से सत्यापित कर सकते हैं।

(i) $\angle 1=\angle 2$

(ii) $\angle 3=\angle 4$

(iii) $\angle 5=\angle 6$

(iv) $\angle 7=\angle 8$

यह क्रियाकलाप निम्नलिखित तथ्य को दृष्टांतित करती है :

यदि दो समांतर रेखाएँ किसी तिर्यक छेदी रेखा द्वारा काटी जाती है, तो संगत कोणों के प्रत्येक युग्म का माप समान होता है।

आकृति 5.18

इस परिणाम का उपयोग करते हुए हम एक दूसरा रुचिकर परिणाम प्राप्त करते हैं। आकृति 5.18 को देखिए।

जब समांतर रेखाएँ $l$ और $m$, रेखा $t$ द्वारा काटी जाती हैं, तो $\angle 3=\angle 7$ (शीर्षाभिमुख कोण) परंतु $\angle 7=\angle 8$ (संगत कोण) इसलिए $\angle 3=\angle 8$ इसी प्रकार आप दर्शा सकते हैं कि $\angle 1=\angle 6$. अतः हमें निम्नलिखित परिणाम की प्राप्ति होती है:

यदि दो समांतर रेखाएँ किसी तिर्यक छेदी रेखा द्वारा काटी जाती हैं, तो अंत: एकांतर कोणों का प्रत्येक युग्म समान होता है।

यह दूसरा परिणाम हमें एक ओर रुचिकर गुणधर्म की ओर अग्रसर करता है। फिर से आकृति 5.18 में दिए हुए आलेख से, $\angle 3+\angle 1=180^{\circ}$ ( $\angle 3$ और $\angle 1$ रैखिक युग्म बनाते हैं) परंतु $\angle 1=\angle 6$ (अंतः एकांतर कोणों का एक युग्म)

इस प्रकार हम कह सकते हैं कि $\angle 3+\angle 6=180^{\circ}$ ।

इसी प्रकार $\angle 1+\angle 8=180^{\circ}$. इस प्रकार हमें निम्नलिखित परिणाम की प्राप्ति होती है :

यदि दो समांतर रेखाएँ किसी एक तिर्यक छेदी रेखा द्वारा काटी जाती हैं तो तिर्यक छेदी रेखा के एक ही तरफ़ को बने अंतः कोणों का प्रत्येक युग्म संपूरक होता है।

सुसंगत आकृतियों को ध्यान में रखते हुए आप इन परिणामों को बहुत आसानी से स्मरण कर सकते हैं:

संगत कोणों के लिए F-आकार को ध्यान में रखिए

एकांतर कोणों के लिए $\mathrm{Z}$ - आकार को ध्यान में रखिए।

इन्हें कीजिए

समांतर रेखाओं का एक युग्म एवं एक तिर्यक छेदी रेखा खींचिए। कोणों को मापकर उपर्युक्त तीन कथनों का सत्यापन कीजिए।

प्रयास कीजिए

5.4 समांतर रेखाओं की जाँच

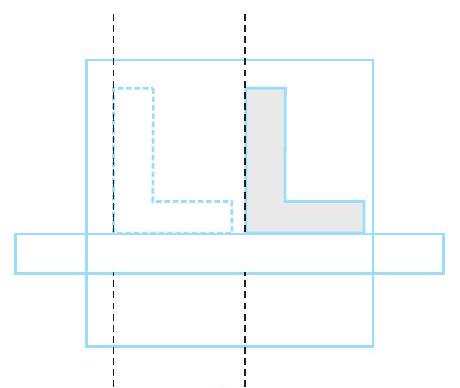
आकृति 5.19

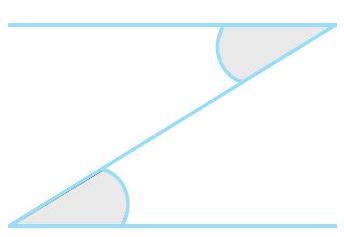
आकृति 5.20

यदि दो रेखाएँ समांतर हैं, तो आप जानते हैं कि एक तिर्यक छेदी रेखा की सहायता से, समान संगत कोणों का एक युग्म प्राप्त होता है, समान अंतः एकांतर कोणों का युग्म प्राप्त होता है और तिर्यक छेदी रेखा के एक ही तरफ़ बनें अंत: कोण, जो संपूरक होते हैं।

जब दो रेखाएँ दी हुई हैं तो क्या कोई ऐसी विधि है जिसकी सहायता से यह जाँच की जा सके कि दी हुई रेखाएँ समांतर हैं अथवा नहीं? जीवन से जुड़ी अनेक परिस्थितियों में आपको इस कौशल की आवश्यकता होती है।

इन खंडों को (आकृति 5.19) खींचने के लिए एक नक्शानवीश, बढ़ई के वर्ग एवं रुलर का प्रयोग करता है। वह दावा करता है कि ये समांतर हैं। कैसे?

क्या आप देख पाते हैं कि उसने संगत कोणों को समान रखा है? (यहाँ तिर्यक छेदी रेखा क्या है?)

अतः जब एक तिर्यक छेदी रेखा दो रेखाओं को इस प्रकार काटती है कि संगत कोणों के युग्म समान हैं, तो रेखाएँ समांतर होती हैं।

अक्षर $\mathrm{Z}$ (आकृति 5.20) को देखिए। यहाँ क्षैतिज खंड समांतर हैं क्योंकि एकांतर कोण समान हैं।

जब एक तिर्यक छेदी रेखा दो रेखाओं को इस प्रकार काटती है कि अंतः एकांतर कोणों का युग्म समान है, तो रेखाएँ समांतर होती हैं।

एक रेखा $l$ खींचिए (आकृति 5.21).

रेखा $l$ के लंबवत् एक रेखा $m$ खींचिए। एक रेखा $p$ इस प्रकार खींचिए ताकि $p$, $m$ के लंबवत् हो। इस प्रकार $p, l$ लंब पर लंब है। आप पाते हैं $p | l$ कैसे? यह इसलिए है क्योंकि आपने $p$ को इस प्रकार खींचा है कि $\angle 1+\angle 2=180^{\circ}$.

अतः जब एक तिर्यक छेदी रेखा दो रेखाओं को इस प्रकार काटती है कि तिर्यक छेदी रेखा के एक ही तरफ़ बने अंतः कोणों का युग्म संपूरक है, तो रेखाएँ समांतर होती हैं।

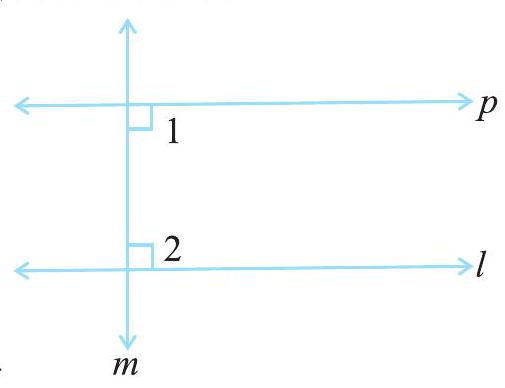
आकृति 5.21

प्रयास कीजिए

प्रश्नावली 5.2

1. निम्नलिखित कथनों में प्रत्येक कथन में उपयोग किए गए गुणधर्म का वर्णन कीजिए (आकृति 5.22)।

(i) यदि $a || b$, तो $\angle 1=\angle 5$

(ii) यदि $\angle 4=\angle 6$, तो $a || b$.

(iii) यदि $\angle 4+\angle 5=180^{\circ}$, तो $a || b$

आकृति 5.22

2. आकृति 5.23 में निम्नलिखित की पहचान कीजिए:

(i) संगत कोणों के युग्म

(ii) अंतः एकांतर कोणों के युग्म

(iii) तिर्यक छेदी रेखा के एक तरफ़ बने अंतःकोणों के युग्म

(iv) शीर्षाभिमुख कोण

आकृति 5.22

3. सलंग्न आकृति में $p || q$ । अज्ञात कोण ज्ञात कीजिए।

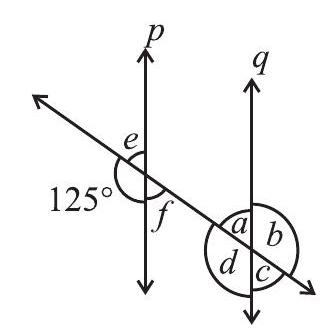
4. यदि $l || m$ है, तो निम्नलिखित आकृतियों में प्रत्येक में $x$ का मान ज्ञात कीजिए।

5. दी हुई आकृति में, दो कोणों की भुजाएँ समांतर हैं। यदि $\angle \mathrm{ABC}=70^{\circ}$, तो

(i) $\angle \mathrm{DGC}$ ज्ञात कीजिए।

(ii) $\angle \mathrm{DEF}$ ज्ञात कीजिए।

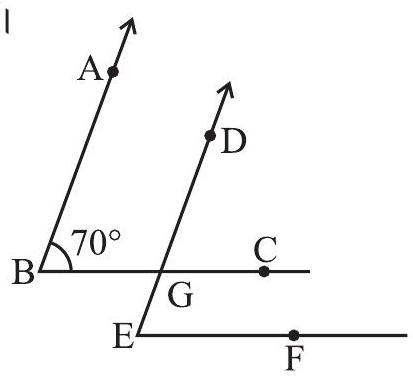
6. नीचे दी हुई आकृतियों में निर्णय लीजिए कि क्या $l, m$ के समांतर है।

हमने क्या चर्चा की ?

1. हम स्मरण करते हैं कि

(i) एक रेखाखंड के दो अंत बिंदु होते हैं।

(ii) एक किरण का केवल एक अंत बिंदु (इसका शीर्ष) होता है।

(iii) एक रेखा का किसी भी तरफ़ कोई अंत बिंदु नहीं होता है।

2. जब दो रेखाएँ $l$ और $m$ एक दूसरे से मिलती हैं तो हम कहते हैं कि ये रेखाएँ प्रतिच्छेद करती हैं। मिलान बिंदु प्रतिच्छेद बिंदु कहलाता है। ऐसी रेखाएँ जिन्हें कितना भी बढ़ाया जाए, आपस में नहीं मिलती, समांतर रेखाएँ कहलाती हैं।