3.1 प्रतिनिधि मान

आप ‘औसत’ (average) शब्द से अवश्य ही परिचित होंगे तथा अपने दैनिक जीवन में औसत शब्द से संबंधित निम्नलिखित प्रकार के कथन अवश्य ही सुने या पढ़े होंगे:

• ईशा अपनी पढ़ाई पर प्रतिदिन औसतन लगभग $5$ घंटे का समय व्यतीत करती है।

• इस समय वर्ष का औसत तापमान $40$ डिग्री (सेल्सियस) है।

• मेरी कक्षा के विद्यार्थियों की औसत आयु $12$ वर्ष है।

• एक स्कूल की वार्षिक परीक्षा के समय विद्यार्थियों की औसत उपस्थिति $98$ प्रतिशत थी। इसी प्रकार के अनेक कथन हो सकते हैं। ऊपर दिए हुए कथनों के बारे में सोचिए।

क्या आप सोचते हैं कि पहले कथन में बताया गया बच्चा प्रतिदिन ठीक $5$ घंटे पढ़ता है? अथवा, क्या उस विशेष समय पर, दिए हुए स्थान का तापमान सदैव $40$ डिग्री रहता है?

अथवा, क्या उस कक्षा के प्रत्येक विद्यार्थी की आयु $12$ वर्ष है? स्पष्टतः इन प्रश्नों का उत्तर है ‘नहीं’ ।

तब, ये कथन हमें क्या बताते हैं?

औसत से हम समझते हैं कि ईशा प्राय: एक दिन में $5$ घंटे पढ़ती है। कुछ दिन वह इससे कम घंटे पढ़ती है और कुछ दिन इससे अधिक घंटे पढ़ती है।

इसी प्रकार, $40$ डिग्री सेल्सियस के औसत तापमान का अर्थ है कि वर्ष के इस समय पर तापमान प्राय: $40$ डिग्री सेल्सियस रहता है। कभी वह $40^{\circ} \mathrm{C}$ से कम रहता है और कभी $40^{\circ}$ $\mathrm{C}$ से अधिक भी रहता है।

इस प्रकार, हम यह अनुभव करते हैं कि औसत एक ऐसी संख्या है जो प्रेक्षणों (observations) या आँकड़ों के एक समूह की केंद्रीय प्रवृत्ति (central tendency) को निरूपित करती (या दर्शाती) है। क्योंकि औसत सबसे अधिक तथा सबसे कम मूल्य (value) के आँकड़ों के बीच में होता है।

इसलिए हम कहते हैं कि औसत, आँकड़ों के एक समूह की केंद्रीय प्रवृत्ति का मापक (measure) है। विभिन्न प्रकार के आँकड़ों की व्याख्या करने के लिए, विभिन्न प्रकार के प्रतिनिधि (representative) या केंद्रीय मानों (central values) की आवश्यकता होती है। इनमें से एक प्रतिनिधि मान अंकगणितीय माध्य या समांतर माध्य (arthmetic mean) है।

3.2 अंकगणितीय माध्य

आँकड़ों के एक समूह के लिए अंधिकांशतः प्रयोग किए जाना वाला प्रतिनिधि मान अंकगणितीय माध्य है, संक्षेप में इसे माध्य (mean) भी कहते हैं। इसे अच्छी प्रकार से समझने के लिए, आइए निम्नलिखित उदाहरण को देखें :

दो बर्तनों में क्रमशः $20$ लीटर और $60$ लीटर दूध है। यदि दोनों बर्तनों में बराबर-बराबर दूध रखा जाए, तो प्रत्येक बर्तन में कितना दूध होगा? जब हम इस प्रकार का प्रश्न पूछते हैं, तब हम अंकगणितीय माध्य ज्ञात करने के लिए कहते हैं।

उपरोक्त स्थिति में, औसत या अंकगणितीय माध्य होगा :

$\frac{\text { दूध की कुल मात्रा }}{\text { बर्तनों की संख्या }}=\frac{20+60}{2} \text { लीटर }=40 \text { लीटर } $

इस प्रकार, प्रत्येक बर्तन में $40$ लीटर दूध होगा।

औसत या अंकगणितीय माध्य (A.M.) या केवल माध्य को निम्नलिखित रूप से परिभाषित किया जाता है:

$ \text { माध्य }=\frac{\text { सभी प्रेक्षणों का योग }}{\text { प्रेक्षणों की संख्या }} $

निम्नलिखित उदाहरणों पर विचार कीजिए:

उदाहरण 1 आशिष तीन क्रमागत दिनों में क्रमशः $4$ घंटे, $5$ घंटे और $3$ घंटे पढ़ता है। उसके प्रतिदिन पढ़ने का औसत समय क्या है?

हल आशिष के पढ़ने का औसत समय होगा :

$ \frac{\text { पढ़ाई में लगाया कुल समय }}{\text { दिनों की संख्या जिनमें पढ़ाई की }}=\frac{4+5+3}{3} \text { घंटे }=4 \text { घंटे प्रतिदिन } $

इस प्रकार, हम कह सकते हैं कि आशिष प्रतिदिन $4$ घंटे के औसत से पढ़ाई करता है।

उदाहरण 2 एक बल्लेबाज ने $6$ पारियों (innings) में निम्नलिखित संख्याओं में रन बनाए : $36,35,50,46,60,55$

एक पारी में उसके द्वारा बनाए गए रनों का माध्य ज्ञात कीजिए।

हल $ \text { कुल रन }=36+35+50+46+60+55=282 $

माध्य ज्ञात करने के लिए, हम सभी प्रेक्षणों का योग ज्ञात करके उसे प्रेक्षणों की कुल संख्या से भाग देते हैं। अतः, इस स्थिति में

माध्य $=\frac{282}{6}=47$.

इस प्रकार, एक पारी में उसके द्वारा बनाए गए रनों का माध्य $47$ है।

प्रयास कीजिए

आप पढ़ाई में व्यतीत किए गए अपने समय (घंटों में) का पूरे सप्ताह का औसत किस प्रकार ज्ञात करेंगे?

सोचिए, चर्चा कीजिए और लिखिए

उपरोक्त उदाहरणों में दिए गए आँकड़ों पर विचार कीजिए तथा निम्नलिखित विषय में सोचिए:

• क्या माध्य प्रत्येक प्रेक्षण से बड़ा है?

• क्या यह प्रत्येक प्रेक्षण से छोटा है?

अपने मित्रों के साथ चर्चा कीजिए। इसी प्रकार का एक और उदाहरण बनाइए और इन्हों प्रश्नों के उत्तर दीजिए।

आप पाएँगे कि माध्य सबसे बड़े और सबसे छोटे प्रेक्षणों के बीच में स्थित होता है।

विशिष्ट रूप में, दो संख्याओं का माध्य सदैव उनके बीच में स्थित होता है।

उदाहरणार्थ, $5$ और $11$ का माध्य $\frac{5+11}{2}=8$ है, जो $5$ और $11$ के बीच में स्थित है।

क्या आप इस अवधारणा का प्रयोग करके, यह दर्शा सकते हैं कि दो भिन्नात्मक संख्याओं के बीच में जितनी चाहें उतनी भिन्नात्मक संख्याएँ ज्ञात की जा सकती हैं?

उदाहरणार्थ $\frac{1}{2}$ और $\frac{1}{4}$ के बीच में आपको इनका औसत मिलेगा $\frac{\frac{1}{2}+\frac{1}{4}}{2}=\frac{3}{8}$ और फिर $\frac{1}{2}$ और $\frac{3}{8}$ के बीच में इनका औसत होगा $\frac{7}{16}$ इत्यादि।

प्रयास कीजिए

1. एक सप्ताह कि अपनी नींद में व्यतीत किए गए समय (घंटों में) का माध्य ज्ञात कीजिए।

2. $\frac{1}{2}$ और $\frac{1}{3}$ के बीच कम से कम पाँच संख्याएँ ज्ञात कीजिए।

3.2.1 प्रसार या परिसर

सबसे बड़े और सबसे छोटे प्रेक्षणों के अंतर से, हमें प्रेक्षणों के प्रसार का एक अनुमान लग जाता है। इसे सबसे बड़े प्रेक्षण में से सबसे छोटे प्रेक्षण को घटा कर ज्ञात किया जा सकता है। हम इस परिणाम को आँकड़ों या प्रेक्षणों का प्रसार या परिसर (range) कहते हैं।

निम्नलिखित उदाहरण देखिए :

उदाहरण 3 एक स्कूल के 10 अध्यापकों की वर्षों में आयु इस प्रकार है :

$ 32,41,28,54,35,26,23,33,38,40 $

(i) सबसे बड़ी उम्र वाले अध्यापक की आयु क्या है? तथा सबसे छोटी उम्र वाले अध्यापक की आयु क्या है?

(ii) अध्यापकों की आयु का परिसर क्या है?

(iii) इन अध्यापकों की माध्य आयु क्या है?

हल

(i) आयु को आरोही क्रम में व्यवस्थित करने पर, हमें प्राप्त होता है :

$ 23,26,28,32,33,35,38,40,41,54 $

हमें ज्ञात होता है कि सबसे बड़ी उम्र वाले अध्यापक की आयु $54$ वर्ष है तथा सबसे छोटी उम्र वाले अध्यापक की आयु $23$ वर्ष है।

(ii) अध्यापकों की आयु का परिसर $=(54-23)$ वर्ष $=31$ वर्ष है।

(iii) अध्यापकों की माध्य आयु

$ \begin{aligned} & =\frac{23+26+28+32+33+35+38+40+41+54}{10} \text { वर्ष } \ & =\frac{350}{10} \text { वर्ष }=35 \text { वर्ष } \end{aligned} $

प्रश्नावली 3.1

1. अपनी कक्षा के किन्हीं दस $(10)$ विद्यार्थियों की ऊँचाइयों का परिसर ज्ञात कीजिए।

2. कक्षा के एक मूल्यांकन में प्राप्त किए गए निम्नलिखित अंकों को एक सारणीबद्ध रूप में संगठित कीजिए :

$ 4,6,7,5,3,5,4,5,2,6,2,5,1,9,6,5,8,4,6,7 $

(i) सबसे बड़ा अंक कौन-सा है?

(ii) सबसे छोटा अंक कौन-सा है?

(iii) इन आँकड़ों का परिसर क्या है?

(iv) अंकगणितीय माध्य ज्ञात कीजिए।

3. प्रथम $5$ पूर्ण संख्याओं का माध्य ज्ञात कीजिए।

4. एक क्रिकेट खिलाड़ी ने $8$ पारियों में निम्नलिखित रन बनाए :

$ 58,76,40,35,46,50,0,100 $

उसका माध्य स्कोर (score) या रन ज्ञात कीजिए।

5. निम्नलिखित सारणी प्रत्येक खिलाड़ी द्वारा चार खेलों में अर्जित किए गए अंकों को दर्शाती है:

अब निम्नलिखित प्रश्नों के उत्तर दीजिए :

(i) प्रत्येक खेल में $\mathrm{A}$ द्वारा अर्जित औसत अंक ज्ञात करने के लिए, माध्य ज्ञात कीजिए।

(ii) प्रत्येक खेल में $\mathrm{C}$ द्वारा अर्जित माध्य अंक ज्ञात करने के लिए, आप कुल अंकों को $3$ से भाग देंगे या $4$ से? क्यों?

(iii) $\mathrm{B}$ ने सभी चार खेलों में भाग लिया है। आप उसके अंकों का माध्य किस प्रकार ज्ञात करेंगे?

(iv) किसका प्रदर्शन सबसे अच्छा है?

6. विज्ञान की एक परीक्षा में, विद्यार्थियों के एक समूह द्वारा ( $100 $ में से) प्राप्त किए गए अंक

$85,76,90,85,39,48,56,95,81$ और $75$ हैं। ज्ञात कीजिए :

(i) विद्यार्थियों द्वारा प्राप्त सबसे अधिक अंक और सबसे कम अंक

(ii) प्राप्त अंकों का परिसर

(iii) समूह द्वारा प्राप्त माध्य अंक

7. छह क्रमागत वर्षों में एक स्कूल में विद्यार्थियों की संख्या निम्नलिखित थी :

$1555,1670,1750,2013,2540,2820$

इस समय काल में स्कूल के विद्यार्थियों की माध्य संख्या ज्ञात कीजिए।

8. एक नगर में किसी विशेष सप्ताह के $7$ दिनों में हुई वर्षा ( $\mathrm{mm}$ में) निम्नलिखित रूप से रिकॉर्ड की गई:

(i) उपरोक्त आँकड़ों से वर्षा का परिसर ज्ञात कीजिए।

(ii) इस सप्ताह की माध्य वर्षा ज्ञात कीजिए।

(iii) कितने दिन वर्षा, माध्य वर्षा से कम रही?

9. $10$ लड़कियों की ऊँचाइयाँ $\mathrm{cm}$ में मापी गईं और निम्नलिखित परिणाम प्राप्त हुए:

$135,150,139,128,151,132,146,149,143,141$.

(i) सबसे लंबी लड़की की लंबाई क्या है?

(ii) सबसे छोटी लड़की की लंबाई क्या है?

(iii) इन आँकड़ों का परिसर क्या है?

(iv) लड़कियों की माध्य ऊँचाई (लंबाई) क्या है?

(v) कितनी लड़कियों की लंबाई, माध्य लंबाई से अधिक है?

3.3 बहुलक

जैसा कि हम पहले बता चुके हैं केवल माध्य ही केंद्रीय प्रवृत्ति का माप या प्रतिनिधि मान नहीं है। विभिन्न प्रकार की आवश्यकताओं के अनुसार अन्य प्रकार कि केंद्रीय प्रवृत्ति के मापकों का प्रयोग किया जाता है।

निम्नलिखित उदाहरण को देखिए :

कमीज़ों के विभिन्न मापों (साइज़ों) की साप्ताहिक माँग को ज्ञात करने के लिए, एक दुकानदार $90 \mathrm{~cm}, 95 \mathrm{~cm}, 100 \mathrm{~cm}, 105 \mathrm{~cm}$ और $110 \mathrm{~cm}$ मापों की कमीज़ों की बिक्री का रिकॉर्ड (record) रखता है। एक सप्ताह का रिकॉर्ड इस प्रकार है :

यदि वह बेची गई कमीज़ों की संख्या का माध्य ज्ञात करे, तो क्या आप सोचते हैं कि वह यह निर्णय ले पाएगा कि किस माप की कमीज़ें स्टॉक (stock) में रखी जाएँ?

$ \text { बेची गई कमीज़ों का माध्य }=\frac{\text { बेची गई कमीज़ों की कुल संख्या }}{\text { कमीज़ों के विभिन्न मापों के प्रकार }}=\frac{105}{5}=21 $

क्या वह प्रत्येक माप की 21 कमीज़ें स्टॉक में रखे? यदि वह ऐसा करता है, तो क्या वह अपने ग्राहकों की आवश्यकताओं को पूरा कर पाएगा?

उपरोक्त रिकॉर्ड को देखकर, दुकानदार $95 \mathrm{~cm}, 100 \mathrm{~cm}$ और $105 \mathrm{~cm}$ मापों की कमीज़ों को मँगवाने का निर्णय लेता है। वह अन्य मापों की कमीज़ों को मँगवाने का निर्णय, उनके कम खरीददारों को देखते हुए, आगे के लिए टाल देता है।

एक अन्य उदाहरण देखिए :

रेडीमेड (readymade) कपड़ों का एक दुकानदार कहता है, ‘मेरे द्वारा सबसे अधिक माप की बेची गईं कमीज़ का माप $90 \mathrm{~cm}$ है।’

ध्यान दीजिए कि यहाँ भी दुकानदार की रुचि विभिन्न मापों की बेची गई कमीज़ों की संख्याओं में ही है। वह कमीज़ के उस माप को देख रहा है, जो सबसे अधिक बिकती है। यह आँकड़ों का एक अन्य प्रतिनिधि मान है। सबसे अधिक बिक्री $105 \mathrm{~cm}$ माप की कमीज़ों की बिक्री है। यह प्रतिनिधि मान (105) आँकड़ों का बहुलक (mode) कहलाता है।

दिए हुए प्रेक्षणों के एक समूह में, सबसे अधिक बार आने वाला प्रेक्षण इस समूह का बहुलक कहलाता है।

उदाहरण 4 निम्नलिखित संख्याओं का बहुलक ज्ञात कीजिए:

$ 1,1,2,4,3,2,1,2,2,4 $

हल समान मान वाली संख्याओं को एक साथ व्यवस्थित करने पर, हमें प्राप्त होता है :

$ 1,1,1,2,2,2,2,3,4,4 $

इन आँकड़ों का बहुलक 2 है, क्योंकि यह अन्य प्रेक्षणों की तुलना में अधिक बार आता है।

प्रयास कीजिए

निम्नलिखित के बहुलक ज्ञात कीजिए:

(i) $2,6,5,3,0,3,4,3,2,4,5,2,4$,

(ii) $2,14,16,12,14,14,16,14,10$, $14,18,14$

3.3.1 बड़े आँकड़ों का बहुलक

यदि प्रेक्षणों की संख्या बड़ी हो, तो उनको समान मान वाले प्रेक्षणों के रूप में व्यवस्थित करना और फिर उनको गिनना इतना सरल नहीं होता है। ऐसी स्थितियों में, हम आँकड़ों को सारणीबद्ध करते हैं, जैसा कि आप पिछली कक्षा में कर चुके हैं, आँकड़ों की सारणी बनाने का कार्य मिलान चिह्नों (tally marks) से प्रारंभ करते हुए, प्रेक्षणों की बारंबारताएँ (frequencies) बना कर पूरा किया जा सकता है।

निम्न उदाहरणों को देखिए :

उदाहरण 5 टीमों के एक समूह में खेले गए फुटबॉल के मैचों में, जीतने के अंतर गोलों में (in goals) निम्नलिखित हैं :

$1,3,2,5,1,4,6,2,5,2,2,2,4,1,2,3,1,1,2,3,2$,

$6,4,3,2,1,1,4,2,1,5,3,3,2,3,2,4,2,1,2$

इन आँकड़ों का बहुलक ज्ञात कीजिए।

हल आइए इन आँकड़ों को एक सारणी के रूप में रखें :

इस सारणी को देखकर, हम तुरंत यह कह सकते हैं कि $’ 2 ‘$ बहुलक है, क्योंकि $2 $ सबसे अधिक बार आया है। इस प्रकार, अधिकांश मैच $ 2$ गोलों के अंतर से जीते गए हैं।

सोचिए, चर्चा कीजिए और लिखिए

क्या संख्याओं के एक समूह में दो बहुलक हो सकते हैं?

उदाहरण 6 निम्नलिखित संख्याओं का बहुलक ज्ञात कीजिए: $2,2,2,3,3,4,5,5,5,6,6,8$

हल यहाँ $2$ और $5$ दोनों ही तीन बार आए हैं। अतः, ये दोनों ही आँकड़ों के बहुलक हैं।

इन्हें कीजिए

1. अपनी कक्षा के साथियों की वर्षों में आयु रिकॉर्ड कीजिए और फिर उनका बहुलक ज्ञात कीजिए।

2. अपनी कक्षा के साथियों की $\mathrm{cm}$ में लंबाइयाँ रिकॉर्ड कीजिए और उनका बहुलक ज्ञात कीजिए।

प्रयास कीजिए

1. निम्नलिखित आँकड़ों का बहुलक ज्ञात कीजिए:

$ 12,14,12,16,15,13,14,18,19,12,14,15,16,15,16,16,15 $

$17,13,16,16,15,15,13,15,17,15,14,15,13,15,14$

2. $25$ बच्चों की ऊँचाइयाँ ( $\mathrm{cm}$ में) नीचे दी गई हैं :

$168,165,163,160,163,161,162,164,163,162,164,163,160,163,160,165$, $163,162,163,164,163,160,165,163,162$

उनकी लंबाइयों का बहुलक क्या है? यहाँ बहुलक से हम क्या समझते हैं?

जहाँ माध्य हमें आँकड़ों के सभी प्रेक्षणें का औसत प्रदान करता है, वहीं बहुलक आँकड़ों में सबसे अधिक बार आने वाले प्रेक्षण को दर्शाता है।

आइए निम्नलिखित उदाहरणों पर विचार करें :

(a) आपको एक दावत में बुलाए गए 25 व्यक्तियों के लिए आवश्यक चपातियों की संख्या के बारे में निर्णय लेना है।

(b) कमीज़ें बेचने वाले एक दुकानदार को अपने स्टॉक की आपूर्ति करनी है।

(c) हमें अपने घर के लिए आवश्यक दरवाज़े की ऊँचाई ज्ञात करनी है।

(d) एक पिकनिक (picnic) पर जाते समय, अगर प्रत्येक व्यक्ति के लिए केवल एक ही फल खरीदा जाना है, तब, हमें कौन-सा फल मिलेगा?

इन स्थितियों में हम किसमें बहुलक का एक अच्छे आकलन के रूप में प्रयोग कर सकते हैं?

पहले कथन पर विचार कीजिए। मान लीजिए प्रत्येक व्यक्ति के लिए आवश्यक चपातियों की संख्या इस प्रकार है :

$2,3,2,3,2,1,2,3,2,2,4,2,2,3,2,4,4,2,3,2,4,2,4,3,5$

इन आँकड़ों का बहुलक $2$ चपाती है। यदि हम बहुलक को आँकड़ों के प्रतिनिधि मान के रूप में प्रयोग करें, तो हमें प्रति व्यक्ति $2$ चपातियों की दर से $25$ व्यक्तियों के लिए केवल $50$ चपातियों की आवश्यकता होगी। परंतु निश्चय ही यह चपातियाँ सभी व्यक्तियों को अपर्याप्त होंगी। इस स्थिति में क्या माध्य एक उपयुक्त प्रतिनिधि मान होगा?

तीसरे कथन के लिए, दरवाज़े की ऊँचाई, उन व्यक्तियों की ऊँचाई से संबंधित है जो उस दरवाज़े का प्रयोग करेंगे। मान लीजिए कि घर में $5$ बच्चे और $4$ वयस्क हैं जो उस दरवाज़े का प्रयोग करते हैं तथा $5$ बच्चों में से प्रत्येक की ऊँचाई $135 \mathrm{~cm}$ के आसपास है। ऊँचाइयों का बहुलक $135 \mathrm{~cm}$ है। क्या हमें एक ऐसा दरवाज़ा लेना चाहिए जिसकी ऊँचाई $144 \mathrm{~cm}$ है? क्या सभी वयस्क इस दरवाज़े में से निकल पाएँगे? यह स्पष्ट है कि इन आँकड़ों के लिए भी बहुलक एक उपयुक्त प्रतिनिधि मान नहीं है। क्या यहाँ माध्य एक उपयुक्त प्रतिनिधि मान होगा?

क्यों नहीं? दरवाज़े की ऊँचाई के बारे में निर्णय लेने के लिए, ऊँचाई के किस प्रतिनिधि मान का प्रयोग किया जाए?

इसी प्रकार, शेष कथनों का विश्लेषण कीजिए तथा इन स्थितियों के लिए उपयुक्त प्रतिनिधि मान ज्ञात कीजिए।

प्रयास कीजिए

अपने मित्रों से चर्चा कीजिए और

(a) दो स्थितियाँ दीजिए, जहाँ प्रतिनिधि मान के रूप में माध्य का प्रयोग उपयुक्त होगा।

(b) दो स्थितियाँ दीजिए, जहाँ प्रतिनिधि मान के रूप में बहुलक का प्रयोग उपयुक्त होगा।

3.4 माध्यक

हम देख चुके हैं कि कुछ स्थितियों में अंकगणितीय माध्य एक उपयुक्त केंद्रीय प्रवृत्ति का मापक है तथा कुछ स्थितियों में बहुलक एक उपयुक्त केंद्रीय प्रवृत्ति का मापक है।

आइए अब एक अन्य उदाहरण देखें। 17 विद्यार्थियों के एक समूह पर विचार कीजिए, जिनकी ऊँचाई $\mathrm{cm}$ में निम्नलिखित हैं :

$106,110,123,125,117,120,112,115,110,120,115,102,115,115,109,115,101$.

खेल की अध्यापिका कक्षा को ऐसे दो समूहों में इस तरह विभाजित करना चाहती है कि प्रत्येक समूह में विद्यार्थियों की संख्या बराबर हो तथा एक समूह में विद्यार्थियों की ऊँचाइयाँ एक विशेष ऊँचाई से कम हों और दूसरे समूह में विद्यार्थियों की ऊँचाइयाँ उस विशेष ऊँचाई से अधिक हों। वह ऐसा किस प्रकार करेगी?

आइए उसके पास जो विभिन्न विकल्प हैं, उन्हें देखें :

(i) वह माध्य ज्ञात कर सकती है। यह माध्य है :

$ \frac{106+110+123+125+117+120+112+115+110+120+115+102+115+115+109+115+101}{17} $

$ =\frac{1930}{17}=113.5 $

अतः, अध्यापिका कक्षा के विद्यार्थियों को यदि ऐसे दो समूहों में विभाजित करती है, जिनमें से एक समूह में माध्य ऊँचाई से कम ऊँचाई वाले विद्यार्थी हैं और दूसरे समूह में माध्य ऊँचाई से अधिक ऊँचाई वाले विद्यार्थी हैं। तब, इन समूहों में विद्यार्थियों की संख्याएँ बराबर नहीं रहती हैं क्योंकि एक समूह में $7$ सदस्य होंगे तथा दूसरे समूह में $10$ सदस्य होंगे।

(ii) उसके पास दूसरा विकल्प है कि वह बहुलक ज्ञात करे। सबसे अधिक बारंबारताओं वाला प्रेक्षण $115 \mathrm{~cm}$ है और इसे बहुलक लिया जाएगा।

बहुलक से नीचे वाले $7$ विद्यार्थी हैं तथा $10$ विद्यार्थी बहुलक के बराबर या उससे ऊपर हैं। अतः, हम कक्षा के विद्यार्थियों को दो बराबर समूहों में विभाजित नहीं कर सकते।

इसलिए, आइए अब हम एक अन्य वैकल्पिक प्रतिनिधि मान या केंद्रीय प्रवृत्ति के मापक के बारे में सोचें। ऐसा करने के लिए, हम पुन: दी हुई ऊँचाइयों ( $\mathrm{cm}$ में) को देखते हैं और इन्हें

आरोही क्रम में व्यवस्थित करते हैं। हम निम्नलिखित प्रेक्षण प्राप्त करते हैं :

$101,102,106,109,110,110,112,115,115,115,115,115,117,120,120,123,125$

प्रयास कीजिए

आपके एक मित्र ने दिए हुए आँकड़ों के माध्यक और बहुलक ज्ञात किए। उस मित्र द्वारा की गई त्रुटि, यदि कोई हो तो, बताइए और सही कीजिए:

$35,32,35,42,38,32,34$

माध्यक $=42$, बहुलक $=32$

इन आँकड़ों में मध्य मान (middle value) $115$ है, क्योंकि यह विद्यार्थियों को दो बराबर समूहों में विभाजित करता है जिनमें से प्रत्येक में $8$ विद्यार्थी हैं। यह मान आँकड़ों का माध्यक (median) कहलाता है। माध्यक उस मान को बताता है, जो आँकड़ों के मध्य में स्थित होता है (उनको आरोही या अवरोही क्रम में व्यवस्थित करने पर) तथा आधे प्रेक्षण इससे अधिक मान वाले होते हैं और आधे प्रेक्षण इससे कम मान वाले होते हैं। खेल की अध्यापिका इस बीच वाले विद्यार्थी को इस खेल में निर्णायक (refree) बना सकती है।

यहाँ हम केवल उन स्थितियों को ही लेंगे, जहाँ प्रेक्षणों की संख्या विषम है।

इस प्रकार, दिए गए आँकड़ों को आरोही या अवरोही क्रम में व्यवस्थित करने के बाद उनका बीचों-बीच (मध्य) वाला मान उनका माध्यक होता है।

ध्यान दीजिए कि सामान्यतः, हमें माध्यक और बहुलक के लिए एक ही मान नहीं मिलेगा। आइए कुछ उदाहरणों को देखें।

उदाहरण 7 निम्नलिखित आँकड़ों का माध्यक ज्ञात कीजिए :

$24,36,46,17,18,25,35$

हल आँकड़ों को आरोही क्रम में व्यवस्थित करने पर, हमें प्राप्त होता है :

$17,18,24,25,35,36,46$

मध्य (बीच) वाला प्रेक्षण माध्यक होता है। अतः, माध्यक 25 है।

प्रश्नावली 3.2

1. गणित की एक परीक्षा में, $15$ विद्यार्थियों द्वारा ( $25$ में से) प्राप्त किए गए अंक निम्नलिखित हैं:

$19,25,23,20,9,20,15,10,5,16,25,20,24,12,20$

इन आँकड़ों के बहुलक और माध्यक ज्ञात कीजिए। क्या ये समान हैं?

2. एक क्रिकेट मैच में खिलाड़ियों द्वारा बनाए गए रन इस प्रकार हैं :

$ 6,15,120,50,100,80,10,15,8,10,15 $

इन आँकड़ों के माध्य, बहुलक और माध्यक ज्ञात कीजिए। क्या ये तीनों समान हैं?

3. एक कक्षा के $15$ विद्यार्थियों के भार ( $\mathrm{kg}$ में) इस प्रकार हैं :

$ 38,42,35,37,45,50,32,43,43,40,36,38,43,38,47 $

(i) इन आँकड़ों के बहुलक और माध्यक ज्ञात कीजिए।

(ii) क्या इनके एक से अधिक बहुलक हैं?

4. निम्नलिखित आँकड़ों के बहुलक और माध्यक ज्ञात कीजिए :

$ 13,16,12,14,19,12,14,13,14 $

5. बताइए कि निम्नलिखित कथन सत्य है अथवा असत्य :

(i) बहुलक आँकड़ों में से सदैव एक संख्या होता है।

(ii) माध्य दिए हुए आँकड़ों में से एक संख्या हो सकता है।

(iii) माध्यक आँकड़ों में से सदैव एक संख्या होता है।

(iv) आँकड़ों $6,4,3,8,9,12,13,9$ का माध्य 9 है।

3.5 भिन्न उद्देश्य के साथ दंड आलेखों का प्रयोग

पिछले वर्ष हम देख चुके हैं कि किस प्रकार एकत्रित (संग्रहित) की गई सूचनाओं को एक बारंबारता बंटन सारणी (frequency distribution table) के रूप में पहले व्यवस्थित करके और फिर इन सूचनाओं को चित्रीय रूप में चित्रालेखों (pictographs) या दंड आलेखों (bargraphs) के रूप में निरूपित किया जाता है। आप इन दंड आलेखों को देख सकते हैं और इनके बारे में निष्कर्ष निकाल सकते हैं। आप इन दंड आलेखों के आधार पर सूचनाएँ भी प्राप्त कर सकते हैं। उदाहरणार्थ, आप कह सकते हैं कि सबसे लंबा दंड (bar) ही बहुलक है, यदि दंड बारंबारता निरूपित करता है।

3.5.1 एक स्केल (या मापदंड) का चुनना

हम जानते हैं कि दंड आलेख समान चौड़ाई के दंडों द्वारा संख्याओं (आँकड़ों) का निरूपण है तथा दंडों की लंबाइयाँ बारंबारताओं और चुने गए स्केल (scale) पर निर्भर करती हैं। उदाहरणार्थ, एक दंड आलेख में, जहाँ संख्याओं को इकाइयों में दर्शाना है, आलेख एक प्रेक्षण के लिए एक इकाई लंबाई निरूपित करता है और यदि उसे संख्याओं को दहाई या सैकड़ों में दर्शाना है, तो एक इकाई लंबाई $10$ या $100$ प्रेक्षणों को निरूपित कर सकती है। निम्नलिखित उदाहरणों पर विचार कीजिए:

उदाहरण 8 छठी और सातवीं कक्षाओं के $200$ विद्यार्थियों से उनके मनपसंद रंग का नाम बताने के लिए कहा गया, ताकि यह निर्णय लिया जा सके कि उनके स्कूल के भवन का क्या रंग रखा जाए। इसके परिणाम निम्नलिखित सारणी में दर्शाए गए हैं। इन आँकड़ों को एक दंड आलेख द्वारा निरूपित कीजिए।

इस दंड आलेख की सहायता से निम्नलिखित प्रश्नों के उत्तर दीजिए :

(i) कौन-सा रंग सबसे अधिक पसंद किया जाता है और कौन-सा रंग सबसे कम पसंद किया जाता है?

(ii) कुल कितने रंग हैं? वे क्या हैं?

हल एक उपयुक्त पैमाना नीचे दर्शाए अनुसार चुनिए :

स्केल को $0$ से प्रारंभ कीजिए। आँकड़ों में सबसे बड़ा मान $55$ है। अतः, स्केल को $55$ से कुछ अधिक, मान लीजिए $60$ पर समाप्त करते हैं। अक्ष पर समान विभाजनों (divisions) का प्रयोग कीजिए, जैसे कि $10$ की वृद्धियाँ। आप जानते हैं कि सभी दंड (bars) $0$ और $60$ के बीच स्थित होंगे। हम स्केल को इस प्रकार चुनेंगे, ताकि $0$ और $60$ के बीच की लंबाई न तो अधिक छोटी हो और न ही अधिक बड़ी हो। यहाँ, हम $1$ इकाई $=10$ विद्यार्थी लेते हैं। फिर हम आकृति में दर्शाए अनुसार, दंड आलेख को खींचते और नामांकित करते हैं। दंड आलेख से हम निष्कर्ष निकालते हैं कि

(i) नीला रंग सबसे मनपसंद रंग है (क्योंकि नीले रंग को निरूपित करने वाला दंड सबसे लंबा है)

(ii) हरा रंग सबसे कम मनपसंद रंग है (क्योंकि हरे रंग को निरूपित करने वाला दंड सबसे छोटा है)।

(iii) यहाँ पांच रंग हैं। ये हैं लाल, हरा, नीला, पीला और नारंगी (ये क्षैतिज अक्ष पर देखे जा सकते हैं)।

उदाहरण 9 निम्नलिखित आँकड़े किसी कक्षा के छः विद्यार्थियों द्वारा ( $600$ में से) प्राप्त किए गए कुल अंकों को दर्शाते हैं। इन्हें एक दंड आलेख द्वारा निरूपित कीजिए।

हल

1. एक उपयुक्त स्केल चुनने के लिए, हम $100$ की वृद्धियाँ लेते हुए, समान विभाजन अक्ष पर अंकित करते हैं। इस प्रकार, $1$ इकाई $100$ अंक निरूपित करेगी। (यदि हम $1$ इकाई से $10$ अंकों को निरूपित करें, तो क्या कठिनाई होगी?)

2. अब आँकड़ों को दंड आलेख द्वारा निरूपित कीजिए।

दोहरे दंड आलेख खींचना

आँकड़ों के निम्नलिखित दो समूहों पर विचार कीजिए, जो दो नगरों, आबेरदीन और मारगेट में, वर्ष के सभी बारह महीनों के लिए, धूप रहने के औसत दैनिक घंटों को दर्शाते हैं। ये नगर दक्षिणी ध्रुव के निकट स्थित हैं और इसीलिए यहाँ प्रतिदिन धूप बहुत कम घंटों के लिए रहती है।

इनके अलग-अलग दंड आलेख खींच कर आप निम्नलिखित प्रकार के प्रश्नों के उत्तर दे सकते हैं:

(i) प्रत्येक नगर में, किस महीने में अधिकतम धूप रहती है? या

(ii) प्रत्येक नगर में, किस महीने में न्यूनतम धूप रहती है?

परंतु ‘एक विशेष महीने में, किस नगर में धूप अधिक घंटों तक रहती है?’ जैसे प्रश्नों के उत्तर देने के लिए, हमें दोनों नगरों के औसत धूप के घंटों की तुलना करने की आवश्यकता होगी। इसके लिए हम उन आलेखों को खींचना सीखेंगे, जिन्हें दोहरे दंड आलेख (double bar graphs) कहा जाता है। इनमें दोनों नगरों की सूचना दंड आलेखों द्वारा साथ-साथ दी हुई होती हैं।

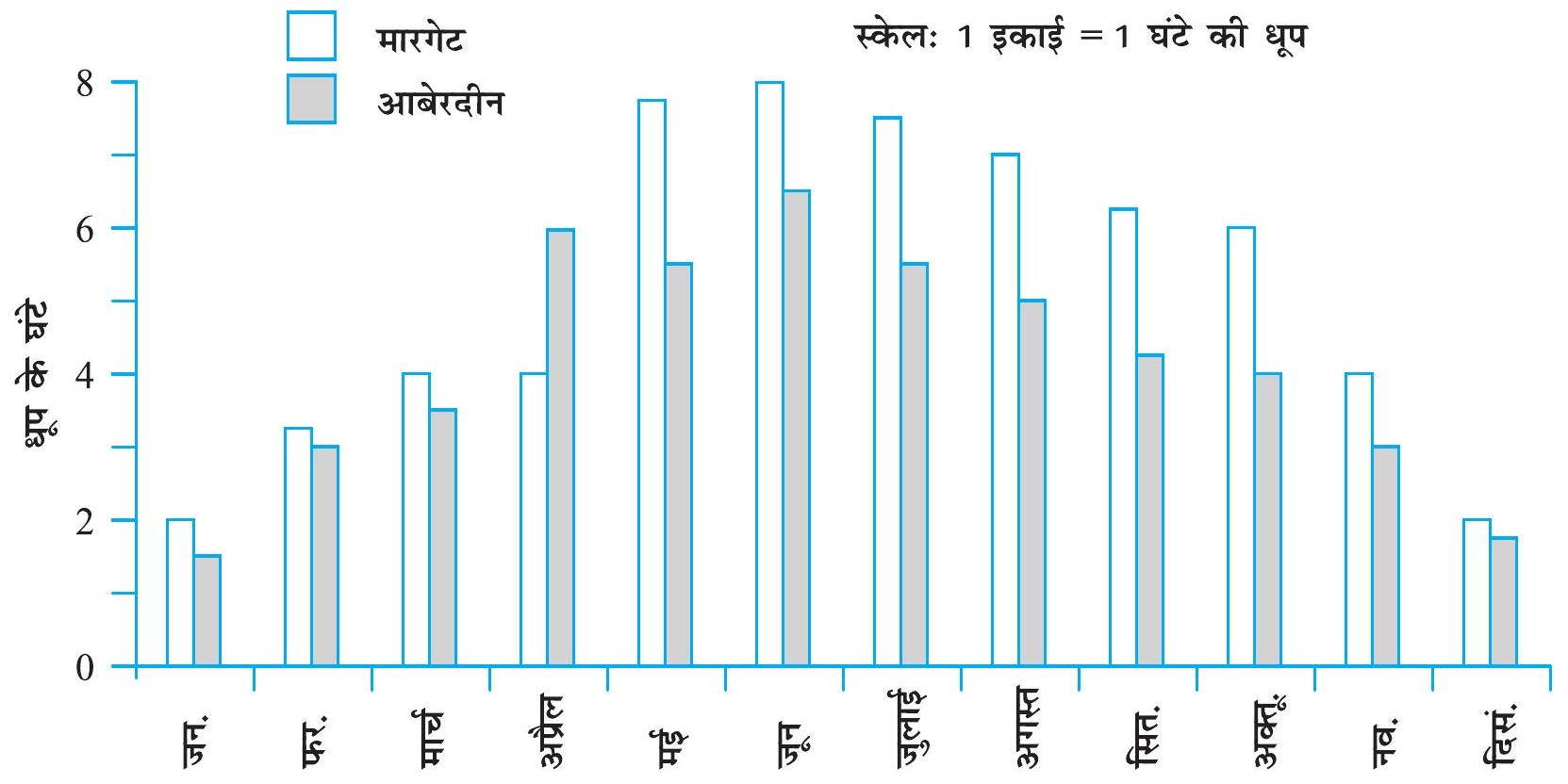
आकृति 3.1

उपरोक्त दंड आलेख (आकृति $3.1$) दोनों नगरों के औसत धूप के समय को दर्शाता है। इसमें प्रत्येक महीने के लिए, हमारे पास दो दंड हैं, जिनकी ऊँचाइयाँ प्रत्येक नगर के औसत धूप के घंटों को दर्शाती हैं। इससे हम यह निष्कर्ष निकाल सकते हैं कि अप्रैल के महीने को छोड़कर, अन्य सभी महीनों में मारगेट में आबेरदीन की अपेक्षा धूप सदैव अधिक रहती है। आप इसी प्रकार का दंड आलेख अपने क्षेत्र या नगर के लिए भी बना सकते हैं।

आइए एक और उदाहरण लें, जो हम से अधिक संबंधित है।

उदाहरण 10 गणित की अध्यापिका यह जानना चाहती है कि तिमाही परीक्षा के बाद, उसके द्वारा पढ़ाई में अपनाई गई नई तकनीक का कोई प्रभाव पड़ा या नहीं। वह सबसे कमजोर $5$ बच्चों द्वारा तिमाही परीक्षा ( $25$ में से) और छःमाही परीक्षा ($25$ में से) में प्राप्त किए अंकों को लेती है, जो इस प्रकार हैं :

हल पहले वह संलग्न आकृति में दर्शाए अनुसार एक दोहरा दंड आलेख (double bar graph) खींचती है। दंडों को देख कर लगता है कि विद्यार्थियों के प्रदर्शन में बहुत सुधार हुआ है। अतः, वह निर्णय लेती है कि उसे अपनी नई शिक्षण तकनीक जारी रखनी चाहिए।

क्या आप कुछ अन्य स्थितियों के बारे में सोचते हैं, जहाँ आप दोहरे दंड आलेखों का प्रयोग कर सकते हैं?

प्रयास कीजिए

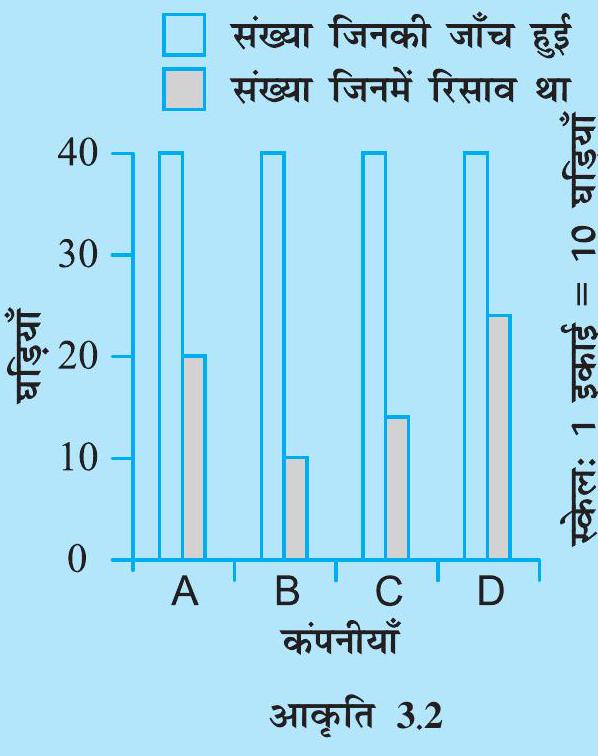
1. दिया हुआ दंड आलेख (आकृति $3.2$), विभिन्न कंपनियों द्वारा बनाई गई जल प्रतिरोधी (Water resistant) घड़ियों की जाँच के लिए किए गए एक सर्वेक्षण को दर्शाता है। इनमें से प्रत्येक कंपनी ने यह दावा किया कि उनकी घड़ियाँ जल प्रतिरोधी हैं। एक जाँच के बाद उपरोक्त परिणाम प्राप्त हुए हैं।

(a) क्या आप प्रत्येक कंपनी के लिए, रिसाव (Leak) वाली घड़ियों की संख्या की, जाँच की गई कुल घड़ियों की संख्या से भिन्न बना सकते हैं?

(b) इसके आधार पर आप क्या बता सकते हैं कि किस कंपनी की घड़ियाँ बेहतर हैं?

2. वर्षों $1995,1996,1997$ और 1998 में, अंग्रेज़ी और हिंदी की पुस्तकों की बिक्री नीचे दी गई हैं :

	$\mathbf{1 9 9 5}$	$\mathbf{1 9 9 6}$	$\mathbf{1 9 9 7}$	$\mathbf{1 9 9 8}$
अंग्रेज़ी	$350$	$400$	$450$	$620$
हिंदी	$500$	$525$	$600$	$650$

एक दोहरा दंड आलेख खींचिए और निम्नलिखित प्रश्नों के उत्तर दीजिए :

(a) किस वर्ष में दोनों भाषाओं की पुस्तकों की बिक्री का अंतर न्यूनतम था?

(b) क्या आप कह सकते हैं कि अंग्रेज़ी की पुस्तकों की माँग में तेज़ी से वृद्धि हुई है? इसका औचित्य समझाइए।

प्रश्नावली 3.3

1. निम्नलिखित प्रश्नों के उत्तर देने के लिए, आकृति $3.3$ में दिए दंड आलेख का प्रयोग कीजिए :

(a) कौन-सा पालतू पशु अधिक लोकप्रिय है?

(b) कितने विद्यार्थियों का पालतू पशु कुत्ता है?

2. निम्नलिखित दंड आलेख को पढ़िए जो एक पुस्तक भंडार द्वारा $5$ क्रमागत वर्षों में बेची गई पुस्तकों की संख्या दर्शाती है, और आगे आने वाले प्रश्नों के उत्तर दीजिए ।

(i) वर्षों $1989,1990$ और $1992$ में से प्रत्येक में लगभग कितनी पुस्तकें बेची गईं?

(ii) किस वर्ष में लगभग $475$ पुस्तकें बेची गईं? किस वर्ष में लगभग $225$ पुस्तकें बेची गईं?

(iii) किन वर्षों में $250$ से कम पुस्तकें बेची गई?

(iv) क्या आप स्पष्ट कर सकते हैं कि आप वर्ष 1989 में बेची गई पुस्तकों का आकलन किस प्रकार करेंगे?

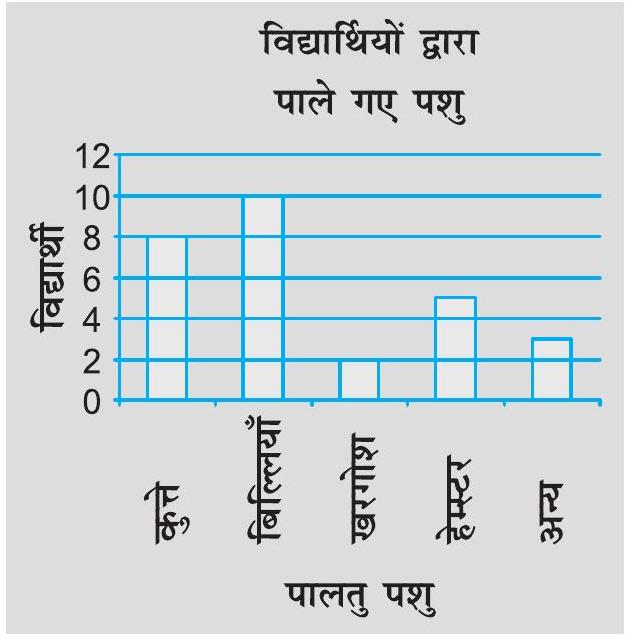
आकृति 3.3

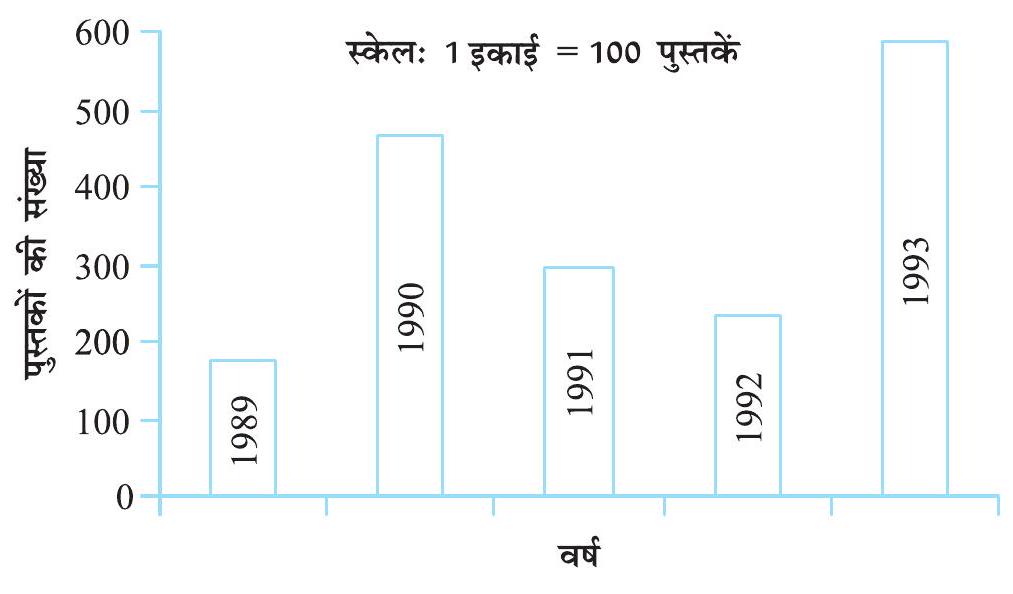
आकृति 3.4

3. छः विभिन्न कक्षाओं के विद्यार्थियों की संख्याएँ नीचे दी गई हैं। इन आँकड़ों को एक दंड आलेख द्वारा निरूपित कीजिए:

(a) आप स्केल किस प्रकार चुनेंगे?

(b) निम्नलिखित प्रश्नों के उत्तर दीजिए :

(i) किस कक्षा में विद्यार्थियों की संख्या अधिकतम है? किस कक्षा में न्यूनतम है?

(ii) कक्षा 6 के विद्यार्थियों की संख्या का कक्षा 8 के विद्यार्थियों की संख्या से अनुपात ज्ञात कीजिए।

4. एक विद्यार्थी के प्रथम सत्र और द्वितीय सत्र का प्रदर्शन दिया हुआ है। एक उपयुक्त स्केल चुनकर एक दोहरा दंड आलेख खींचिए और दिए गए प्रश्नों के उत्तर दीजिए:

(i) किस विषय में विद्यार्थी ने अपने प्रदर्शन में सबसे अधिक सुधार किया है?

(ii) किस विषय में सुधार सबसे कम है?

(iii) क्या किसी विषय में प्रदर्शन नीचे गिरा है?

5. किसी कॉलोनी में किए गए सर्वेक्षण से प्राप्त निम्नलिखित आँकड़ों पर विचार कीजिए :

(i) एक उपयुक्त स्केल चुनकर, एक दोहरा दंड आलेख खींचिए। इस दंड आलेख से आप क्या निष्कर्ष निकालते हैं?

(ii) कौन-सा खेल अधिक लोकप्रिय हैं?

(iii) खेलों को देखना अधिक पसंद किया जाता है या उनमें भाग लेना?

6. इस अध्याय के प्रारंभ में, दिए हुए विभिन्न नगरों के न्यूनतम और अधिकतम तापमानों के आँकड़ों (सारणी 3.1) को लीजिए। इन आँकड़ों का एक दोहरा दंड आलेख खींच कर निम्नलिखित प्रश्नों के उत्तर दीजिए :

(i) दी हुई तिथि पर किस नगर के न्यूनतम और अधिकतम तापमान का अंतर सबसे अधिक है?

(ii) कौन-सा नगर सबसे गर्म है और कौन-सा नगर सबसे ठंडा है।

(iii) ऐसे दो नगरों के नाम लिखिए, जिनमें से एक का अधिकतम तापमान दूसरे के न्यूनतम तापमान से कम था।

(iv) उस नगर का नाम लिखिए, जिसके न्यूनतम और अधिकतम तापमानों का अंतर सबसे कम है।

हमने क्या चर्चा की?

1. औसत एक ऐसी संख्या है, जो दिए हुए प्रेक्षणों के समूह (या आँकड़ों) का प्रतिनिधित्व करता है या उनकी केंद्रीय प्रवृत्ति को दर्शाता है।

2. अंकगणितीय माध्य आँकड़ों का एक प्रतिनिधि मान है।

3. बहुलक केंद्रीय प्रवृत्ति या प्रतिनिधि मान का एक अन्य रूप है। प्रेक्षणों के एक समूह का बहुलक वह प्रेक्षण है जो सबसे अधिक बार आता है।

4. माध्यक भी एक प्रकार का प्रतिनिधि मान है। यह उस मान को दर्शाता है, जो प्रेक्षण के मध्य (बीच) में होता है (उन्हें आरोही या अवरोही क्रम में व्यवस्थित करने के बाद) तथा आधे प्रेक्षण इसके ऊपर होते हैं और आधे प्रेक्षण इसके नीचे होते हैं।

5. इकट्ठे किए आँकड़ों को बारंबारता बंटन सारणी की सहायता से चित्रीय रूप से दंड आलेखों के रूप में दर्शाया जा सकता है। दंड आलेख संख्याओं या आँकड़ों का समान चौड़ाई वाले दंडों द्वारा एक चित्रीय निरूपण है।

6. हमने यह भी सीखा है कि एक दोहरा दंड आलेख किस प्रकार खींचा जाता है। यह एक ही दृष्टि में, प्रेक्षणों के दो समूहों की तुलना करने में सहायक रहता है।