अध्याय 07 गति एवं दूरियों का मापन
पहेली तथा बूझो की कक्षा के सभी बच्चों के बीच ग्रीष्मावकाश में भ्रमण किए गए स्थानों के बारे में सामान्य चर्चा हो रही थी। एक बच्चा अपने पैतृक गाँव पहले रेलगाड़ी, फिर बस और अंत में बैलगाड़ी का उपयोग करके गया था। एक विद्यार्थी ने वायुयान से यात्रा की थी। एक अन्य विद्यार्थी ने अवकाश के अनेक दिन अपने चाचा जी की नाव में सैर करके मछली पकड़ने में व्यतीत किए थे।
इसके पश्चात् अध्यापक ने विद्यार्थियों से समाचारपत्र के उन लेखों को पढ़ने के लिए कहा जिनमें उन छोटे पहियों वाले वाहनों के बारे में वर्णन है, जो मंगल ग्रह की धरती पर चले थे और प्रयोग भी किए। इन वाहनों को मंगल तक ले जाने का कार्य अंतरिक्षयान द्वारा किया गया था।
इसी बीच पहेली प्राचीन भारत के बारे में कहानियाँ पढ़ती रही तथा अब वह यह जानना चाहती है कि प्राचीन काल में लोग एक स्थान से दूसरे स्थान की यात्रा कैसे करते थे?
7.1 यातायात की कहानी
प्राचीन काल में लोगों के पास यातायात के कोई साधन नहीं थे। वे पैदल चलते थे तथा अपना सामान अपनी पीठ पर लादकर ले जाते थे। बाद में मानव यातायात के लिए पशुओं का उपयोग करने लगा।
प्राचीन काल में जल मार्गों में आने-जाने के लिए नावों का उपयोग किया जाता था। आरंभ में लकड़ी के लट्टों से जिनमें खोखली गुहिका बनाई जा सके, नावें बनाई जाती थीं। इसके पश्चात् लोगों ने लकड़ी के विभिन्न टुकड़ों को आपस में जोड़कर नाव की आकृति बनाना सीख लिया। ये नावें जल में रहने वाले जीवों की आकृतियों के सदृश थीं। अध्याय 5 एवं 6 में मछलियों की धारा रेखीय आकृति से संबंधित चर्चा को याद कीजिए।
पहिए के आविष्कार ने यातायात की प्रणाली में अत्यंत महत्वपूर्ण परिवर्तन किए। पिछले हज़ारों वर्षों में पहिए के डिज़ाइन में सुधार किए गए हैं। पहियों पर चलने वाली गाड़ियों को खींचने के लिए पशुओं का उपयोग किया जाता था।
उन्नीसवीं शताब्दी के प्रारंभ तक भी लोग एक स्थान से दूसरे स्थान तक परिवहन के लिए पशुओं, नावों तथा जहाजों पर निर्भर करते थे। वाष्प-इंजन के आविष्कार से परिवहन के नए साधनों का विकास हुआ। वाष्प-इंजन से चालित सवारी-गाड़ियों तथा माल-गाड़ियों के डिब्बों के लिए रेल की पटरियों का

चित्र 7.1 परिवहन के कुछ साधन
निर्माण किया गया। इसके पश्चात् मोटर कार, ट्रक तथा बस जैसे स्वचालित वाहन आए। जल पर परिवहन के साधन के रूप में मोटर से चलने वाली नाव और जहाज़ों का उपयोग होने लगा। उन्नीसवीं शताब्दी के प्रारंभ के वर्षों में वायुयान का विकास हुआ जिनमें बाद में सुधार किए गए और इन्हें यात्री तथा सामान ले जाने योग्य बनाया गया। विद्युत-रेलगाड़ी, एकल-रेल (एक पटरी रेल), पराध्वनिक (सुपरसोनिक) वायुयान तथा अंतरिक्षयान बीसवीं शताब्दी के कुछ योगदान हैं।
चित्र 7.1 में परिवहन के विभिन्न साधन दर्शाए गए हैं। इन्हें प्राचीनतम से अत्याधुनिक परिवहन के साधनों के सही क्रम में व्यवस्थित कीजिए।
क्या इनमें परिवहन का कोई ऐसा प्राचीन साधन भी हैं जिसे आजकल उपयोग में नहीं लाया जाता है?
7.2. यह डेस्क कितना चौड़ा है?
लोग यह कैसे पता लगाते थे कि वे कितनी दूर चले हैं?
आप यह कैसे पता लगाएँगे कि आप अपने स्कूल तक की दूरी पैदल चलकर तय कर सकते हैं अथवा स्कूल पहुँचने के लिए आपको बस अथवा रिक्शे की आवश्यकता होगी? जब आपको कुछ खरीदना होता है, तब क्या आपके लिए बाज़ार तक पैदल जाना संभव होता है? आप इन प्रश्नों के उत्तर कैसे जानेंगे?
कोई स्थान कितना दूर है, यह प्राय: जानना महत्वपूर्ण होता है, ताकि हम यह अनुमान लगा सकें कि वहाँ पहुँचने के लिए हम कैसे जाएँगें — पैदल चलकर, बस से, रेलगाड़ी से, पानी के जहाज़ से, वायुयान से अथवा कोई अंतरिक्षयान लेना होगा!
कभी-कभी ऐसी वस्तुएँ भी होती हैं, जिनकी लंबाई अथवा चौड़ाई जानने की हमें आवश्यकता होती है।
पहेली तथा बूझो की कक्षा के कमरे में बड़े-बड़े डेस्क हैं जिन पर दो-दो विद्यार्थी बैठते हैं। पहेली तथा बूझो एक डेस्क पर साथ-साथ बैठते हैं, परंतु बहुधा उनमें इस बात को लेकर झगड़ा होता रहता है कि उसका दूसरा साथी डेस्क के अधिक भाग का उपयोग कर रहा है। अध्यापक के सुझाव पर उन्होंने डेस्क की लंबाई मापने का निश्चय किया। डेस्क के ठीक मध्य में एक चिह्न बनाया तथा डेस्क को दो बराबर भागों में बाँटने के लिए एक रेखा खींची।
ये दोनों ही अपने मित्रों के साथ गिल्ली-डंडा खेलने के शौकीन हैं और बूझो तो सदैव ही अपने पास एक गिल्ली और एक डंडा रखता है।
चित्र 7.2 गिल्ली तथा डंडे से डंस्क की लंबाई मापना
यहाँ चित्र 7.2 में देखिए। उन्होंने गिल्ली और डंडे का उपयोग करके डेस्क की लंबाई मापने का प्रयास कैसे किया है।
ऐसा लगता है कि डेस्क की लंबाई, दो डंडों की लंबाई तथा दो गिल्लियों की लंबाई के योग के बराबर है। डेस्क के मध्य में रेखा खींचने पर दोनों प्रसन्न दिखाई देते हैं क्योंक दोनों को आधा-आधा डेस्क मिल गया है, जिसमें डेस्क का आधा भाग, लंबाई में, एक डंडे और एक गिल्ली की लंबाई के बराबर है। कुछ दिनों के बाद खींची गई रेखा मिट जाती है। बूझो का पुराना गिल्ली-डंडा खो गया है। अब उसके पास गिल्ली-डंडे का नया सेट है। अब देखिए वे गिल्ली-डंडे के नए सेट का उपयोग करके डेस्क की लंबाई किस प्रकार मापते दिखाई देते हैं (चित्र 7.3)।
चित्र 7.3 गिल्ली-डंडे के किसी भिन्न सेट से डेस्क की लंबाई मापना
हैलो! अब जब डेस्क की लंबाई गिल्ली-डंडे के नए सेट से मापी गई तब डेस्क की लंबाई ऐसी प्रतीत हुई जैसे यह लगभग दो डंडों तथा एक गिल्ली की लंबाइयों के बराबर हो परंतु फिर भी डेस्क का कुछ भाग बच जाता है। यह तो एक गिल्ली की लंबाई से कम है! अब क्या करें?
आप पहेली और बूझो को क्या सुझाव देंगे ताकि वे डेस्क की पूरी लंबाई माप लें। क्या वे लंबाई मापने के लिए क्रिकेट के विकेट तथा गुल्लियों का उपयोग कर सकते हैं अथवा आप सोचते हैं कि ऐसा करने से वैसी ही समस्या उत्पन्न हो सकती है?
वह एक कार्य कर सकते हैं, एक छोटी डोरी लें और इस पर दो चिह्न लगाएँ। यह डोरी की एक लंबाई होगी। वे डेस्क की चौड़ाई डोरी की लंबाई के पदों में माप सकते हैं (चित्र 7.4)। वे इस डोरी का उपयोग डोरी की लंबाई से कम दूरियों को मापने में किस प्रकार कर सकते हैं? वे डोरी को मोड़ कर ‘डोरी की लंबाई’ का आधा (
आप यह भी कह सकते हैं कि इन्हें अपने ज्यामिति-बॉक्स के पैमाने को उपयोग करके अपनी समस्या हल करनी चाहिए। हाँ, वास्तव में ऐसा किया जा सकता है।
बूझो ने यह पढ़ा है कि जब ऐसे मानक पैमाने नहीं थे तब लोग दूरियाँ कैसे मापते थे तथा वह स्वयं भी भिन्न-भिन्न ढंगों से दूरियाँ मापने का प्रयास कर चुका है।

चित्र 7.4 डोरी की लंबाई से डेस्क की लंबाई का मापन
ऐसे अनेक अवसर आते हैं जब हमें लंबाई अथवा दूरियाँ मापने की आवश्यकता होती है। दर्ज़ी कपड़े की लंबाई यह जानने के लिए मापता है कि वह कपड़ा कुर्ता सीने के लिए पर्याप्त है अथवा नहीं। बढ़ई किसी अलमारी की लंबाई तथा चौड़ाई इसलिए मापता है ताकि वह यह जान सके कि इस अलमारी के दरवाज़े को बनाने के लिए कितनी लकड़ी की आवश्यकता होगी। किसी किसान को अपने खेत की लंबाई तथा चौड़ाई अथवा उसके क्षेत्रफल जानने की इसलिए आवश्यकता होती है ताकि वह यह जान जाए कि वह अपने खेत में कितने बीज बो सकता है तथा उसे अपनी फसलों के लिए कितने जल की आवश्यकता होगी।
यदि आप से पूछा जाए कि आपकी लंबाई कितनी है तब आप एक ऐसी सरल रेखा की लंबाई बताएँगे जो आपके सिर से आपके पैर की एड़ी तक की रेखीय लंबाई के बराबर है।
यह कमरा कितना लंबा है?
यह डेस्क कितना चौड़ा है?
दिल्ली, लखनऊ से कितनी दूर है?
पृथ्वी से चंद्रमा कितनी दूर है?
इन सभी प्रश्नों में एक बात समान है। ये सभी दो स्थानों के बीच की दूरी से संबंधित हैं। दो स्थान, मेज़ के दो किनारों की तरह, पास-पास हो सकते हैं। इसके विपरीत दो स्थान जम्मू और कन्याकुमारी की तरह, एक-दूसरे से बहुत दूर भी हो सकते हैं।
आइए, अब हम कुछ मापन यह जानने के लिए करते हैं कि जब हम दूरियाँ अथवा लंबाइयाँ मापते हैं, तो हमें सही रूप में क्या करना आवश्यक होता है?
7.3 कुछ मापन
क्रियाकलाप 1
आप इस क्रियाकलाप को समूह में एक-एक करके कीजिए। अपने पैर की लंबाई को लंबाई का एक मात्रक मानकर अपनी कक्षा के कमरे की लंबाई तथा
चौडाई मापिए। इन्हें मापते समय यह संभव है कि आपको यह पता चले कि कुछ भाग मापने से बच गया है तथा यह भाग आपके पैर की लंबाई से छोटा है। पहले ही की भाँति अपने पैर के भाग की लंबाई मापने के लिए किसी डोरी का उपयोग कीजिए। अपने प्रेक्षणों को सारणी 7.1 में लिखिए।
सारणी 7.1 : कक्षा की लंबाई और चौड़ाई मापना
विद्यार्थी का
नामकक्षा के कमरे की
लंबाईकक्षा के
कमरे की
चौड़ाई
क्रियाकलाप 2
समूह में कार्य कीजिए। आप में प्रत्येक अपने बालिश्त को मानक मात्रक मानकर अपनी कक्षा के कमरे में रखी मेज़ अथवा डेस्क की चौड़ाई माप सकते हैं (चित्र 7.5)।

चित्र 7.5 मेज की चौड़ाई को बालिश्त से मापना
मापन के लिए यहाँ भी आप यह पाते हैं कि आपको अपनी एक बालिश्त के बराबर लंबी डोरी तथा इस डोरी की लंबाई के अंश भागों की आवश्यकता होती है।
अपने प्रेक्षणों को सारणी 7.2 में लिखिए। हम देखते हैं कि मापन का अर्थ किसी अज्ञात राशि की उसी प्रकार की कुछ ज्ञात राशि से तुलना करना है। इस ज्ञात निश्चित राशि को मात्रक कहते हैं। किसी माप के परिणाम को दो भागों में व्यक्त किया जाता है। एक भाग संख्या है। दूसरा भाग ली गई माप का मात्रक होता
सारणी 7.2 : मेज़ा की चौड़ाई मापना
मेज़ की चौड़ाई
किसने मापी?बालिश्तों
की संख्या
है। उदाहरण के लिए क्रियाकलाप 1 में यदि कक्षा के कमरे की लंबाई आपके 12 पैर की लंबाई के बराबर है तो 12 एक संख्या है तथा ‘पैर की लंबाई’ एक मात्रक है जिसे मापन के लिए चुना गया है।
अब सारणी 7.1 तथा 7.2 में अंकित सभी मापों का अध्ययन कीजिए। क्या प्रत्येक पैर द्वारा मापी गई कमरे की लंबाई के ये सभी माप बराबर हैं? क्या सभी के द्वारा अपनी-अपनी बालिश्तों से मापी गई मेज़ की चौड़ाई की माप बराबर है? शायद ये परिणाम भिन्न-भिन्न हो सकते हैं, क्योंकि आपकी बालिश्त लंबाई में आपके मित्रों की बालिश्तों से भिन्न हो सकती है। इसी प्रकार सभी विद्यार्थियों के पैर की लंबाइयों में भी कुछ अंतर हो सकता है। इसलिए जब आप अपने बालिश्तों या पैरों की लंबाई को मात्रक की भाँति उपयोग करके किए गए माप को किन्ही अन्य व्यक्तियों को बताते हैं, तो वे यह नहीं समझ पाते कि यह लंबाई वास्तव में कितनी है, क्योंकि वास्तविक लंबाई जानने के लिए बालिश्त अथवा पैर की लंबाई जानना आवश्यक है।
अतः हम देखते हैं कि हमें मापन के कुछ ऐसे मात्रकों की आवश्यकता है, जो सभी व्यक्तियों के लिए समान हों।
7.4 मापन के मानक मात्रक
प्राचीन काल में पैर की लंबाई, अंगुली की चौड़ाई तथा एक कदम की दूरी, इन सभी मापों का मात्रक के रूप में सामान्य उपयोग होता था।
हड़प्पा सभ्यता के लोगों ने अवश्य ही लंबाई के बहुत अच्छे मापन का उपयोग किया होगा, क्योंकि यह खुदाई में प्राप्त परिशुद्ध ज्यामितीय रचनाओं को देखने से प्रमाणित होता है।
कोहनी से अंगुली के छोर तक की लंबाई जिसे हाथ कहते हैं, लंबाई के मात्रक के रूप में प्राचीन मिस्न में उपयोग किया जाता था जिसे संसार के अन्य भागों में भी मान्यता प्राप्त थी।
संसार के विभिन्न भागों में लोग लंबाई के मात्रक के रूप में ‘फुट’ का उपयोग करते थे। अलग-अलग क्षेत्रों में फुट की लंबाई थोड़ी भिन्न थी।
लोग एक गज़ कपड़ा फैली बाँह के सिरे से अपने ठोड़ी तक मापते थे। रोमवासी अपने पग अथवा कदमों से लंबाई मापते थे।
प्राचीन भारत में छोटी लंबाइयों को मापने के लिए अंगुल अथवा मुट्ठी का उपयोग किया जाता था। आज भी भारत के कई शहरों में हम पुष्प विक्रेताओं को पुष्प हारों को बेचते समय अपनी भुजाओं का उपयोग लंबाई के मात्रक के रूप में करते हुए देख सकते हैं। सुविधानुसार शरीर के ऐसे बहुत-से भागों का मात्रकों के रूप में उपयोग होता रहा है।
तथापि प्रत्येक व्यक्ति के शरीर की आमापों में थोड़ी भिन्नता हो सकती है। शायद इसी कारण भी मापन में उलझनें आई होंगी। वर्ष 1790 में, फ्रांसीसियों ने मापन की एक मानक प्रणाली की रचना की जिसे ‘मीटरी पद्धति’ कहते हैं।
एक समानता के लिए समस्त संसार के वैज्ञानिकों ने मापन के मानक मात्रकों के एक सेट को स्वीकार कर लिया है। आजकल जिस मात्रक-प्रणाली का उपयोग हो रहा है, उसे ‘अंतर्राष्ट्रीय मात्रक प्रणाली’ (S.I.मात्रक) कहते हैं। लंबाई का S.I. मात्रक मीटर है। चित्र 7.6 में मीटर पैमाना दिखाया गया है। इसमें आपके ज्यामिति-बॉक्स का 15 सेंटीमीटर पैमाना भी दिखाया गया है।
प्रत्येक मीटर (m) को 100 बराबर भागों में विभाजित किया जाता है, जिन्हें सेंटीमीटर (cm) कहते हैं। एक सेंटीमीटर के दस बराबर भाग होते हैं जिन्हें मिलीमीटर (
लंबी दूरियों के मापन के लिए मीटर एक सुविधाजनक मात्रक नहीं है। इसके लिए हम एक बड़े मात्रक को परिभाषित करते हैं। इसे किलोमीटर
अब हम अपने सभी मापन क्रियाकलापों को मानक पैमानों का उपयोग करके दोहरा सकते हैं तथा लंबाइयों को S.I. मात्रकों में माप सकते हैं। ऐसा करने से पहले हमें दूरियाँ तथा लंबाइयाँ मापने का सही ढंग जानना आवश्यक है।
7.5 लंबाई की यथार्थ ( परिशुद्ध ) माप
अपने दैनिक जीवन में हम विविध प्रकार की मापक युक्तियों का उपयोग करते हैं। लंबाई मापने के लिए हम मीटर पैमाने का उपयोग करते हैं। दर्ज़ी मापक फीते का उपयोग करता है, जबकि कपडे़े के व्यापारी मीटर छड़ काम में लाते हैं। किसी वस्तु की लंबाई मापने के लिए आपको किसी उपयुक्त युक्ति का चयन करना चाहिए। उदाहरण के लिए किसी वृक्ष का घेर अथवा अपने सीने (वक्ष) की माप के लिए आप मीटर पैमाने का उपयोग नहीं कर सकते। ऐसी मापों के लिए मापक फीता अधिक सुविधाजनक होता है। छोटी
चित्र 7.6 मीटर पैमाना तथा 15 सेंटीमीटर पैमाना
लंबाइयाँ जैसे, आपकी पेंसिल की लंबाई, मापने के लिए आप अपने ज्यामिति-बॉक्स के 15 सेंटीमीटर पैमाने को काम में ला सकते हैं।
(a)
(b)
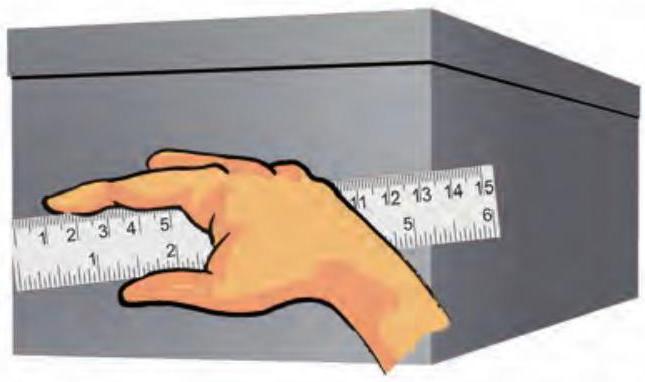
चित्र 7.7 मापी जाने वाली लंबाई के अनुदिश पैमाना रखने की (a) सही तथा (b) गलत विधि
लंबाई मापते समय हमें निम्नलिखित सावधानियाँ बरतने की आवश्यकता होती है-
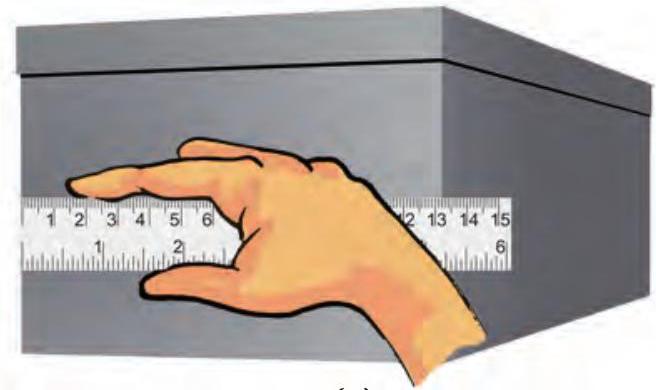
1. चित्र 7.7 में दिखाए अनुसार पैमाने को वस्तु के संपर्क में इसकी लंबाई के अनुदिश रखिए।
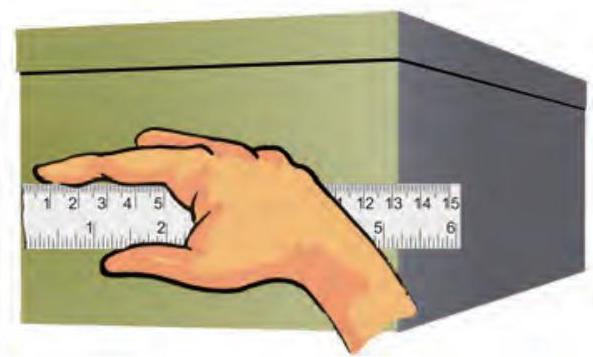
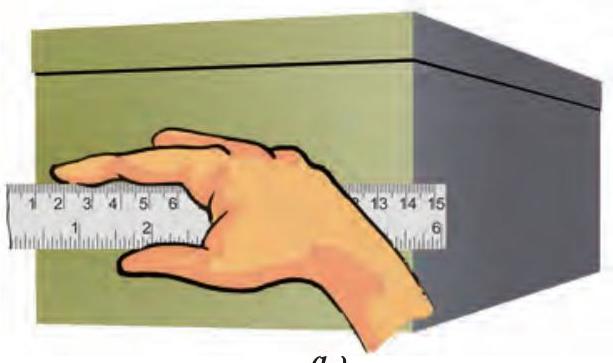
2. कुछ पैमानों के सिरे टूटे हो सकते हैं। आप इन पैमानों के शून्यांक स्पष्ट नहीं देख सकेंगे। [(चित्र 7.8 (a)] ऐसे प्रकरणों में, पैमाने के शून्यांक से माप लेने से बचिए। आप पैमाने का कोई अन्य पूर्णांक, जैसे 1.0 सेंटीमीटर [(चित्र 7.8 (b)] काम में ला सकते हैं। तब आपको दूसरे सिरे के पाठ्यांक से इस पूर्णांक के पाठ्यांक को घटाना चाहिए। उदाहरण के लिए चित्र 7.8 (b) में एक सिरे का पाठ्यांक 1.0 सेंटीमीटर तथा दूसरे सिरे का पाठ्यांक
(a)
(b)
चित्र 7.8 टूटे किनारे वाले पैमाने को रखने की (a) सही तथा (b) गलत विधि
3. माप लेने के लिए आँख की सही स्थिति भी महत्वपूर्ण होती है। चित्र 7.9 में दर्शाए अनुसार आपकी आँख, जिस बिंदु की माप ली जानी है उसके ठीक सामने होनी चाहिए। स्थिति

चित्र 7.9 पैमाने के उचित पाठ्यांक के लिए आँख की स्थिति
क्रियाकलाप 3
अपने सहपाठी की ऊँचाई पहले बालिश्तों और फिर मीटर पैमाने का उपयोग करके मापिए। इसके लिए
सारणी 7.3 : ऊँचाई का मापन
ऊँचाई
किसने मापीऊँचाई
बालिश्त मेंऊँचाई
सेंटीमीटर में
अपने सहपाठी को दीवार के साथ पीठ रखकर खड़ा होने के लिए कहिए। उसके सिर से ठीक ऊपर दीवार पर एक चिह्न अंकित कीजिए। अब फर्श से दीवार पर बने इस चिह्न तक की दूरी पहले अपने बालिश्त से और फिर मीटर पैमाने से मापिए। अन्य सभी विद्यार्थियों से इस लंबाई को इसी प्रकार मापने के लिए कहिए। सभी प्रेक्षण सारणी 7.3 में लिखिए।
विभिन्न विद्यार्थियों के द्वारा प्राप्त परिणामों का ध्यान से अध्ययन कीजिए। कॉलम-2 में परिणाम एक-दूसरे से भिन्न हो सकते हैं क्योंकि विद्यार्थियों के बालिश्तों की लंबाई एक-दूसरे से भिन्न हो सकती है। अब कॉलम-3 के परिणामों को देखिए जिसमें सभी मापें मानक पैमाने द्वारा ली गई हैं। ये परिणाम एक-दूसरे के बहुत समीप हो सकते हैं? परंतु क्या ये एक-दूसरे के ठीक-ठीक बराबर हैं? यदि नहीं, तो आपके विचार से यह अंतर क्यों है? आखिर सभी एक ही पैमाने का उपयोग कर रहे हैं, भिन्न-भिन्न बालिश्तों का उपयोग तो कर नहीं रहे। यह अंतर प्रेक्षण लेने में होने वाली छोटी त्रुटियों के कारण हो सकता है। मापन की इन त्रुटियों को जानने और व्यवहार में लाने के महत्त्व के बारे में उच्च कक्षाओं में सीखेंगें।
7.6 किसी वक्र-रेखा की लंबाई मापना
हम किसी वक्र-रेखा की लंबाई सीधे ही मीटर पैमाने का उपयोग करके नहीं माप सकते। वक्र-रेखा की लंबाई मापने के लिए हम धागे का उपयोग कर सकते हैं।
क्रियाकलाप 4
वक्र रेखा
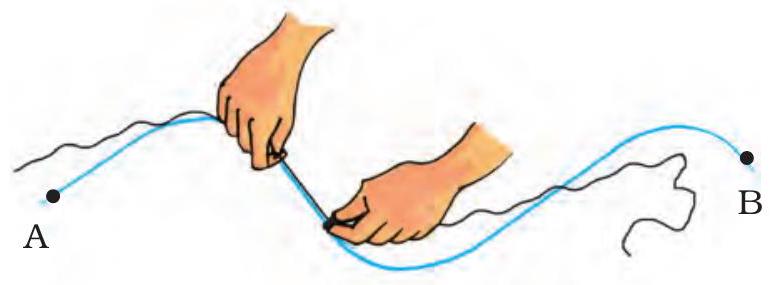
चित्र 7.10 धागे की सहायता से किसी वक्र-रेखा की लंबाई मापना
हमने देखा कि यह सुनिश्चित करने के लिए कि हम दूरियों तथा लंबाइयों की यथार्थ माप ले रहे हैं, हमें बहुत-सी सावधानियाँ बरतनी पड़ती हैं। मापन के लिए कुछ मानक युक्तियों तथा मापन परिणामों को व्यक्त करने के लिए हमें कुछ मानक मात्रकों की आवश्यकता होती है।
7.7 हमारे चारों ओर गतिशील वस्तुएँ
क्रियाकलाप 5
उन वस्तुओं के बारे में सोचिए जो आपने हाल ही में देखी हैं। इनकी सूची सारणी 7.4 में बनाइए। आपकी
सारणी 7.4 : विराम और गतिशील वस्तुएँ
विराम में वस्तु गतिशील वस्तु घर एक उड़ती चिड़िया मेज़ घड़ी में सेकंड की सुई घड़ी
सूची में स्कूल का बस्ता, मच्छर, मेज़, कुर्सियों पर बैठे व्यक्ति, इधर-उधर जाते लोग आदि हो सकते हैं। इसके अतिरिक्त तितलियाँ, कुत्ते, गाय, आपका हाथ, छोटा बच्चा, जल में मछली, घर, फ़ैक्ट्री, पत्थर, घोड़ा, गेंद, बल्ला, चलती रेलगाड़ी, सिलाई मशीन, दीवार घड़ी, घड़ी की सुइयाँ भी हो सकती हैं। आप जितनी लंबी सूची बना सकते हों, बनाइए।
इनमें से कौन गतिशील है और कौन विराम में है? आपने यह कैसे सुनिश्चित किया कि कोई वस्तु गति में है अथवा विराम में है?
आपने यह देखा होगा कि चिड़िया कुछ समय पश्चात् पहले वाले स्थान पर दिखाई नहीं देती, जबकि मेज़ उसी स्थान पर है। इस आधार पर आपने यह सुनिश्चित किया होगा कि कोई वस्तु गति में है अथवा विराम में है।
आइए, हम किसी चींटी की गति को ध्यान से देखते हैं।
क्रियाकलाप 6
कोई ऐसा स्थान चुनिए जहाँ चींटियाँ हों। इस स्थान के निकट कागज़ की एक बड़ी शीट फैलाकर इस पर कुछ चीनी रखिए। चींटियाँ इस चीनी की ओर आकर्षित होंगी तथा आप शीघ्र ही इस कागज़ की शीट पर बहुत-सी चींटियों को रेंगते हुए देखेंगे। किसी एक चींटी के लिए जब वह कागज़ की शीट पर तुरंत रेंग चुकी हो पेंसिल से उसकी स्थितियों के निकट छोटे-छोटे चिह्न अंकित कीजिए (चित्र 7.11)। जैसे-जैसे यह

चित्र 7.11 किसी चींटी की गति
कागज़ पर रेंगती जाए आप इसकी स्थितियों पर चिह्न अंकित करते जाइए। कुछ समय के पश्चात् कागज़ की शीट को इधर-उधर हिलाकर इस पर से चीनी एवं चींटययाँ हटा दीजिए। उन विभिन्न बिंदुओं, जिन्हें आपने कागज़ पर अंकित किया था, को तीरों द्वारा जोड़कर चींटी की गति की दिशा दर्शाइए। वह हर बिंदु जिसे आपने अंकित किया है कुछ सेकंडों के समय अंतराल में चींटी ने कहाँ-कहाँ गति की, को दर्शाता है।
गति किसी वस्तु की स्थिति में किसी प्रकार के परिवर्तन जैसी दिखाई देती है, क्या आप ऐसा नहीं मानते?
क्रियाकलाप 5 में वस्तुओं के समूह बनाते समय आपने घड़ी, सिलाई की मशीन अथवा बिजली का पंखा जैसी वस्तुओं को किस समूह में रखा था? क्या ये वस्तुएँ एक स्थान से दूसरे स्थान तक गति कर रही हैं? नहीं! क्या आप इनके किसी भाग में कोई गति देखते हैं? पंखें की पंखुड़याँ अथवा घड़ी की सुइयाँ कैसी गति करती हैं? क्या इनकी गति चींटी अथवा रेलगाड़ी की गति जैसी है? आइए, अब हम कुछ प्रकार की गतियाँ देखते हैं जिनसे हमें इन विभिन्न प्रकार की गतियों को समझने में सहायता मिलेगी।
7.8 गति के प्रकार
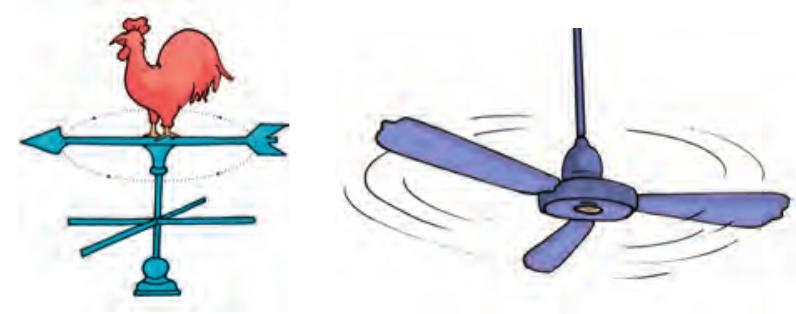
आपने सीधी सड़क पर किसी वाहन की गति, किसी परेड में सिपाहियों के मार्च-पास्ट की गति अथवा किसी गिरते पत्थर की गति का प्रेक्षण किया होगा (चित्र 7.12)। यह किस प्रकार की गति है?
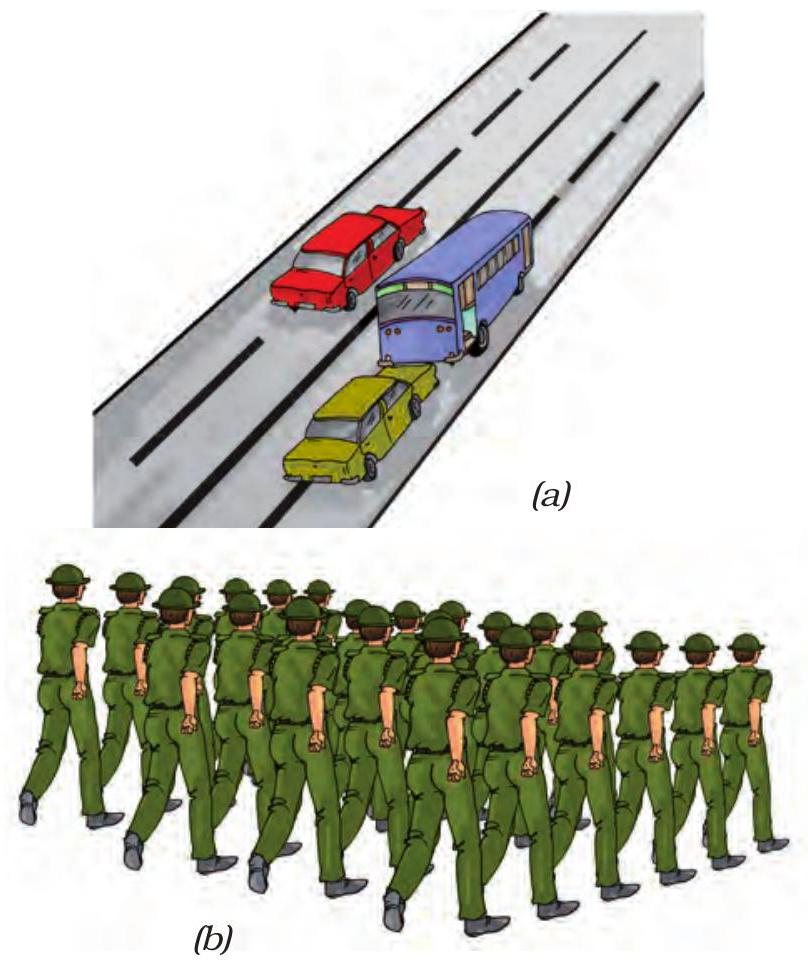
चित्र 7.12 सरल रेखीय गति के कुछ उदाहरण
इन सभी उदाहरणों में हम यह देखते हैं कि वस्तुएँ सरल रेखा के अनुदिश गति कर रही हैं। इस प्रकार की गति को सरल रेखीय गति कहते हैं।
क्रियाकलाप 7
एक पत्थर लीजिए। इससे एक धागा बाँधिए तथा अपने हाथ से इसे तेज़ी से घुमाइए। पत्थर की गति को ध्यान से देखिए। हम देखते हैं कि पत्थर वृत्तीय पथ के अनुदिश गति कर रहा है।
(a)
(c)
चित्र 7.13 वर्तुल गति करती कुछ वस्तुएँ
इस गति में पत्थर की आपके हाथ से दूरी समान रहती है। इस प्रकार की गति को वर्तुल गति कहते हैं।
बिजली के पंखें की पंखुड़ियों पर अंकित किसी चिह्न की गति किसी घड़ी के सेकंड की सुई की गति वर्तुल गति के उदाहरण हैं। (चित्र 7.13)
बिजली का पंखा अथवा घड़ी स्वयं एक स्थान से दूसरे स्थान तक गति नहीं कर रहे हैं। परंतु पंखे की पंखुड़ियाँ घूर्णन करती हैं तथा ऐसा ही घड़ी की सुइयाँ भी करती हैं। यदि हम पंखें की पंखुड़ययों अथवा घड़ी की सुइयों पर कहीं किसी प्रकार का कोई चिह्न अंकित कर दें तो घूर्णन करते समय भी पंखें अथवा घड़ी के केंद्र से इस चिह्न की दूरी समान रहेगी।
कुछ प्रकरणों में कोई वस्तु एक निश्चित समय

बूझो यह निश्चित नहीं कर पा रहा है कि जब हम पत्थर को तेज़ी से घुमाते हैं तब हम यह क्यों कहते हैं कि पत्थर की हाथ से दूरी समान रहती है। क्या आप बृझो को यह समझने में सहायता कर सकते हैं? याद रखिए पत्थर डोरी से बँधा हुआ है।
अंतराल के बाद अपनी गति को दोहराती है। इस प्रकार की गति को आवर्वी गति कहते हैं। डोरी से बँधा हुआ वही पत्थर लीजिए जिसे आपने क्रियाकलाप 7 में उपयोग किया था। अब डोरी को अपने हाथ में थामिए तथा पत्थर को डोरी से लटकने दीजिए। यह एक लोलक है। दूसरे हाथ से पत्थर को एक तरफ खींचिए और फिर स्वतंत्र गति करने के लिए छोड़ दीजिए। लोलक की यह गति आवर्ती गति का एक उदाहरण है। वृक्ष की शाखाओं का इधर-उधर लहराना, झूला झूलते बच्चे की गति, सितार की डोरियों की गति, बजते समय ढोलों (अथवा तबलों) की झिल्ली की गति ये सभी आवर्ती गति के उदाहरण हैं जिनमें वस्तुएँ एक निश्चित समय अंतराल के बाद अपनी गति को दोहराती हैं (चित्र 7.14)।
क्या आपने क्रियाकलाप 5 के एक भाग के रूप में सिलाई की मशीन का प्रेक्षण किया था? आपने ध्यान दिया होगा कि सिलाई मशीन अपनी इसी अवस्थिति पर रहती है जबकि उसका पहिया वर्तुल गति में होता है। इसमें एक सुई भी होती है जो जब तक पहिया घूर्णन करता है, तब तक निरंतर ऊपर-नीचे गति करती रहती है, क्या ऐसा नहीं है? यहाँ सुई आवर्ती गति कर रही है।
क्या आपने फ़र्श पर लुढ़कती किसी गेंद की गति का ध्यानपूर्वक प्रेक्षण किया है? यहाँ गेंद किसी फ़र्श

चित्र 7.14 आवर्ती गति के उदाहरण
पर लुढ़कती और घूर्णन करती हुई आगे की ओर गति करती है। इस प्रकार गेंद सरल रेखीय गति के साथ-साथ घूर्णन गति भी करती है। क्या आप ऐसे अन्य उदाहरण बता सकते हैं जिनमें वस्तु की गति विभिन्न प्रकार की गतियों से मेल करती है?
इस अध्याय के अंतर्गत हमने बहुत से मापनक्रियाकलाप किए हैं तथा कुछ प्रकार की गतियों के विषय में चर्चा की है। हमने देखा कि समय के साथ स्थिति में परिवर्तन को गति कहते हैं। स्थिति में हुए इस परिवर्तन को हम दूरी-मापन द्वारा ज्ञात कर सकते हैं।
इससे हमें यह जानकारी मिलती है कि कोई वस्तु कितनी धीमी अथवा तीव्र गति कर रही है। फ़र्श पर घोंघे का रेंगना, तितली का एक पुष्प से दूसरे पुष्प पर मंडराना, नदी का प्रवाहित होना, वायुयान का वायु में ऊँचाइयों पर उड़ना, पृथ्वी के परित: चंद्रमा द्वारा गति करना, हमारे शरीर में रुधिर का परिसंचरण आदि सभी उदाहरण हमारे चारों ओर अनेक स्थानों पर होने वाली गतियों को दर्शाते हैं।
प्रमुख शब्द
वर्तुल गति दूरी मापन गति आवर्ती गति सरलरेखीय गति SI मात्रक मापन के मात्रक
सारांश
एक स्थान से दूसरे स्थान तक जाने के लिए परिवहन के विभिन्न साधनों का उपयोग किया जाता है।
प्राचीन काल में लोग पैर की लंबाई, अंगुली की चौड़ाई, एक कदम की दूरी आदि का उपयोग मापन के मात्रक के रूप में करते थे। इससे उलझनें होती थीं तथा इसीलिए किसी एक समान मापन प्रणाली को विकसित करने की आवश्यकता उत्पन्न हुई।
अब हम मात्रकों की अंर्तराष्ट्रीय प्रणाली (S.I. मात्रक) उपयोग करते हैं। इसे समस्त संसार में मान्यता प्राप्त है।
S.I. मात्रकों में लंबाई का मानक मात्रक मीटर है।
सरल रेखा के अनुदिश गति को सरल रेखीय गति कहते हैं।
वर्तुल गति में कोई वस्तु इस प्रकार गति करती है कि उस वस्तु की किसी नियत बिंदु से दूरी समान रहती है।
ऐसी गति जो एक निश्चित समय अंतराल के पश्चात् दोहराती है, उसे आवर्ती गति कहते हैं।
अभ्यास
1. वायु, जल तथा थल पर उपयोग किए जाने वाले परिवहन के साधनों में प्रत्येक के दो उदाहरण लिखिए।
2. रिक्त स्थानों की पूर्ति कीजिए:
(क) एक मीटर में _____________ सेंटीमीटर होते हैं।
(ख) पाँच किलोमीटर में _____________ मीटर होते हैं।
(ग) झूले पर किसी बच्चे की गति _____________ होती है।
(घ) किसी सिलाई मशीन की सुई की गति _____________ होती है।
(ङ) किसी साइकिल के पहिए की गति _____________ होती है।
3. पग अथवा कदम का उपयोग लंबाई के मानक मात्रक के रूप में क्यों नहीं किया जाता?
4. निम्नलिखित को लंबाई के बढ़ते परिमाणों में व्यवस्थित कीजिए।
1 मीटर, 1 सेंटीमीटर, 1 किलोमीटर, 1 मिलीमीटर
5. किसी व्यक्ति की लंबाई 1.65 मीटर है। इसे सेंटीमीटर तथा मिलीमीटर में व्यक्त कीजिए।
6. राधा के घर तथा उसके स्कूल के बीच की दूरी 3250 मीटर है। इस दूरी को किलोमीटर में व्यक्त कीजिए।
7. किसी स्वेटर बुनने की सलाई की लंबाई मापते समय स्केल पर यदि इसके एक सिरे का पाठ्यांक 3.0 सेंटीमीटर तथा दूसरे सिरे का पाठ्यांक 33.1 सेंटीमीटर है तो सलाई की लंबाई कितनी है?
8. किसी चलती हुई साइकिल के पहिए तथा चलते हुए छत के पंखे की गतियों में समानताएँ तथा असमानताएँ लिखिए।
9. आप दूरी मापने के लिए किसी लचीले फीते का उपयोग क्यों नहीं करते? यदि आप किसी दूरी को लचीले फीते से मापें तो अपनी माप को किसी अन्य को बताने में आपको जो समस्याएँ आएँगी उनमें से कुछ समस्याएँ लिखिए।
10. आवर्ती गति के दो उदाहरण लिखिए।
प्रस्तावित परियोजनाएँ एवं क्रियाकलाप
1. अपनी कक्षा के कमरे का मानचित्र खींचिए। उसके फ़र्श पर गेंद लुढ़काइए। अपने मानचित्र में जहाँ से गेंद ने लुढ़कना आरंभ किया था और जहाँ वह रुकी थी, वे बिंदु दर्शाइए। जिस पथ के अनुदिश उसने गति की उसे भी दर्शाइए। क्या गेंद किसी सरल रेखा के अनुदिश चली थी?
2. डोरी तथा स्केल का उपयोग करके प्रत्येक विद्यार्थी से उसके पैर की लंबाई का मापन कराइए। समस्त कक्षा के विद्यार्थियों के पैरों की लंबाई की माप प्राप्त करके स्तंभ ग्राफ खींचिए।