Let s Make Patterns From a Drop of Colour

Make your pattern
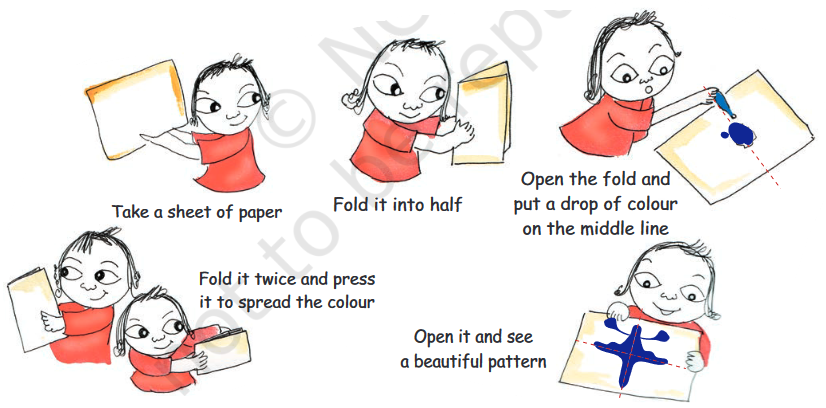
Can you cut this pattern in such a way that you get two similar mirror halves? In how many ways can you do it?
Look at this pattern.
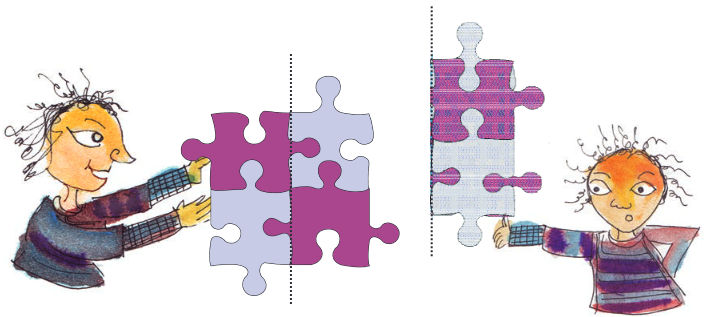
The dotted line divides the shape into two halves. But if you fold it along the dotted line, the left half does not cover the right half completely. So the two halves are not mirror halves.
Now look at another shape.
If you fold it along the dotted line, one half will cover the other similar half completely. So the two here are mirror halves.
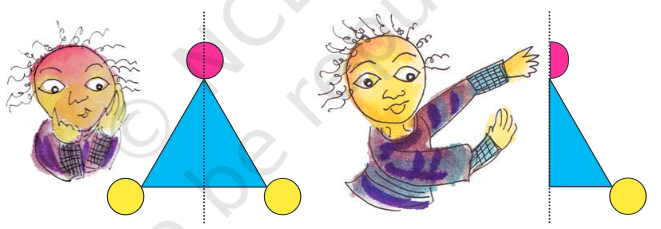
Now imagine the same for these pictures.

On the next page, children need to understand that even though the shape is symmetric, the colour scheme of the figure can make it asymmetric (e.g. in shapes 10 and 12). Encourage children to look for asymmetry based on the shape as well as the colour scheme.
❈ Which shapes are divided into two mirror halves by the dotted line?

Mirror Games
1. Here is a picture of a dog. You can place a mirror on the dotted line. Then the part of the dog to the right of the line will be hidden behind the mirror. What you will see is like (a).
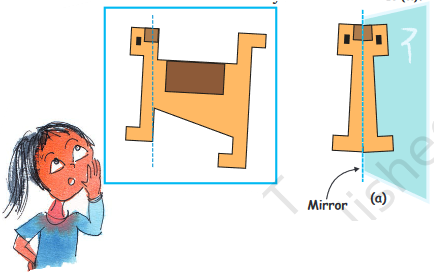
Look at the figure in the white box. On which of the dotted lines will you keep the mirror so that you get shape (b)? Also tell which part of the picture will be hidden when we keep the mirror on the dotted line.
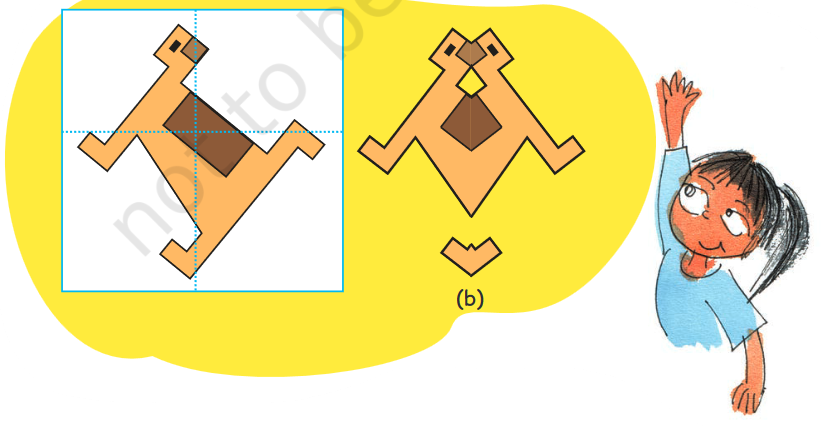
Now make a line on the white box to show where you will keep the mirror to get the picture next to it.
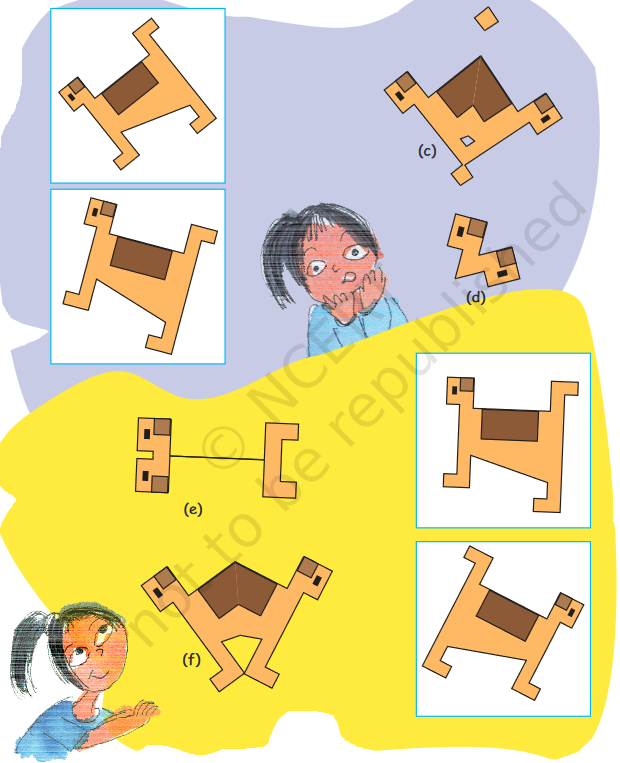
2. Venky has made a red and white shape. Make a line on the white box where you will keep a mirror to get that shape. Look at how the line is drawn in the first box to get the picture next to it.
Half A Turn
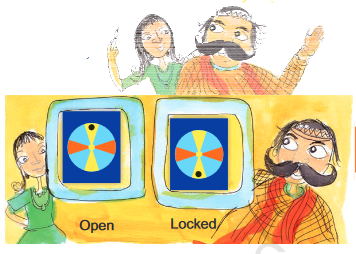
Once there was a king. He was upset because thieves kept stealing costly jewels from his locker. Here is what the locker looked like:

The locker could be opened by giving its handle half a turn. Another half turn and the locker would be locked again.
The king would often leave the locker open thinking it was locked. Can you guess the reason?

One day his clever daughter gave him an idea which he liked very much.
Now he never got confused.
Can you guess what the idea was? The king’s daughter asked the king to put a dot on one of the yellow blades.
The king had many such lockers with different handles. Check if, on giving them half a turn, he can get confused with these too.

What will you do to solve the problem for each of these?
Same after $\frac{1}{2}$ turn?
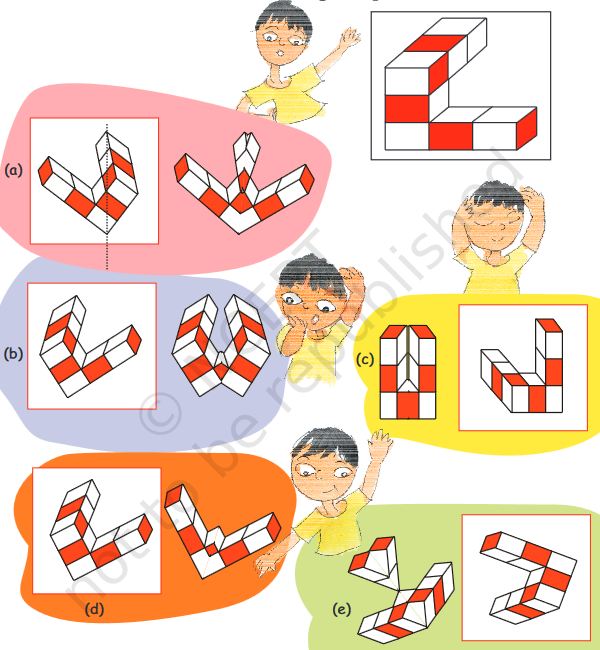
Guess which of the shapes below would look the same after half a turn.

The focus of the exercise following the story (on the next page) is to (i) break the symmetry of the figures. (ii) recreate the symmetry in the same figure.
Do you find it difficult to tell? If yes, then there is a way to check your guess. Here’s how you can do it.
Take any of the shapes. Trace its outline on a sheet of paper. Now keep the shape on its outline and give it a half turn. See if the shape fits its outline.

Practice time

1) Find out which letters in the English alphabet look the same after half a turn.
2) Which of these English words reads the same on half a turn?
Zoom, Mow, Swims, Sis, Noon
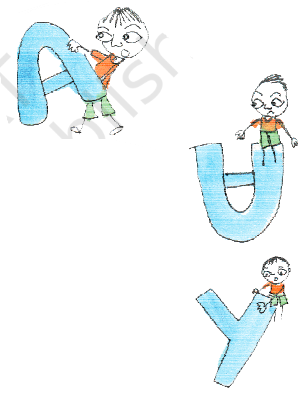
3) Give half a turn to the numbers from 0 to 9. Find which of them still looks the same.
4) Think of all 2, 3 and 4 digit numbers which look the same on half a turn.
Example
2 digit numbers 11 , _______, _______
3 digit numbers 101 , 111, ______, ______, ______, _____, _____, ______
4 digit numbers 1001, 1111, _____, _____, _____, _____, _____
5) Which among the following pictures will look the same on half a turn?
Activity Time
Have you ever seen a windmill? What is it used for? Let us make a toy windmill.
1. Take a sheet of paper.
2. Fold it as shown in the picture.
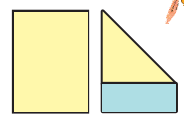
3. Cut out the blue part of the paper. Your sheet of paper will now look like a square.

4. Fold it along the red lines and then open the fold. Draw a circle on the sheet as shown in the picture.

5. Cut along the red lines till you reach the circle. The paper will look like this.
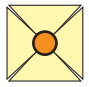
6. Take a pin and make holes on the four corners as shown in the picture.
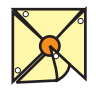
7. Now fold the corners such that all the holes lie one on top of the other.

8. Pass the pin through the holes and fix it in the stick.
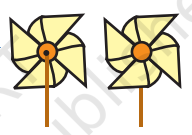
Your windmill is ready. Run with it and see how fast it moves.
❈ Does your windmill look the same on $\frac{1}{4}$ of a turn?
❈ Does it look the same on half a turn? Discuss.
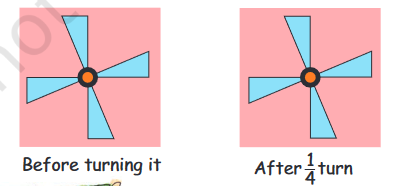
One-Fourth Turn
Does the fan look the same on $\frac{1}{4}$ turn?
Will this fan also look the same after $\frac{1}{4}$ turn? Draw in the yellow box.
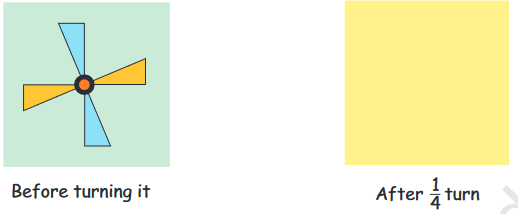
Practice time
A) ❈ Among the following shapes, find out which ones would look the same after $\frac{1}{4}$ turn. Put a $ (\checkmark )$.
Put a ( X ) on the shapes that will not look the same after half a turn

B) Try and change the shapes in such a way that the new shape remains the same on giving it half a turn.

C) Draw what the following shapes would look like on $\frac{1}{4}$ turn and half a turn.
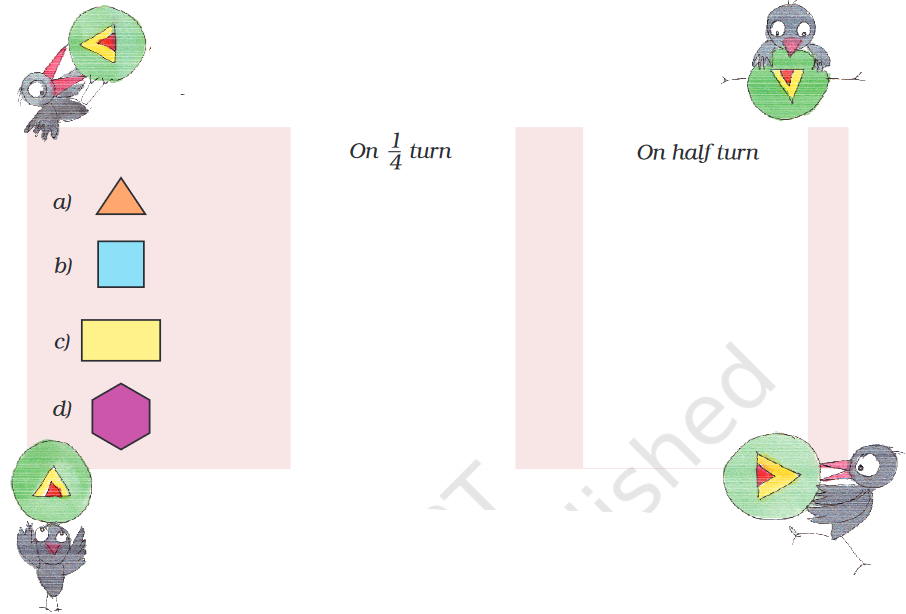
Which of the above shapes do not look the same on $\frac{1}{4}$ turn? Which shapes do not look the same on $\frac{1}{2}$ a turn?
❈ Which fan will look the same on a $\frac{1}{3}$ turn ?

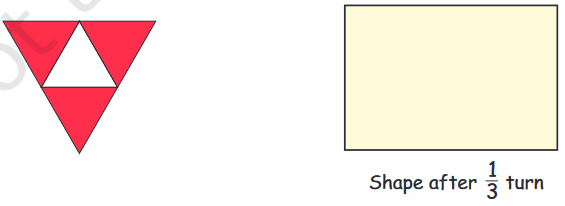
❈ Draw this shape after $\frac{1}{3}$ turn
One-Sixth Turn
Can you see that this shape looks the same on $\frac{1}{6}$ turn?

Practice Time
1. Look at the following shapes. Draw how they will look on $\frac{1}{3}$ and $\frac{1}{6}$ turn.
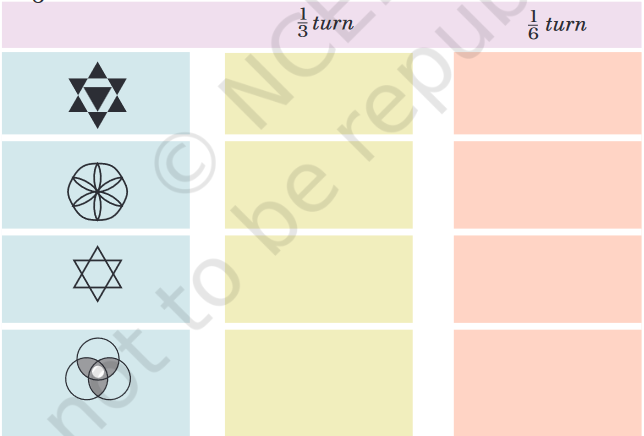
Encourage children to look at the figure and see what kind of a symmetry is there. If they need they can draw six lines to see how to rotate a figure through $\frac{1}{6}$ turn. They should also be able to see that a figure which looks the same on $\frac{1}{6}$ turn will also look the same on $\frac{1}{3}$ turn (which is the same as two $\frac{1}{6}$ turns).
2. Look at the following shapes —
a) Find out which of these figures look the same on $\frac{1}{3}$ turn. Mark them with $(\checkmark)$.
b) Which are the ones that will not look the same after $\frac{1}{3}$ turn? Mark them with (X).

c) Try and change the shapes below in such a way that they look the same on $\frac{1}{3}$ turn.

3. Draw some shapes which will look the same after $\frac{1}{3}$ turn.
4. Draw some shapes which will look the same after $\frac{1}{6}$ turn.










